基于直觉模糊集的公私合营项目方案选择
商克俭,冯东梅,李乃文
(辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105)
0 引言
在PPP项目的整个生命周期中以项目方案的选择最为重要。项目方案的选择从决策科学角度来说属于多属性决策问题,目前国内学者的研究中,如:陈婷婷等[1]用AHP-TOPSIS法对地铁车站的设计方案的选择研究,田林钢等[2]用基于改进的熵权-TOPSIS法对震损水库最佳除险加固方案的选择研究等,普遍存在两个问题:一是存在信息损失的问题,即专家无法完整地表达评价意见。主要原因是在传统的多属性群体决策方法和模糊决策方法中,专家只能用一个实数或区间数来表达自己对于被评价事物的意见。而该种方法的缺点是其无法反映出经典的心理学事实——语言上的否定并不一定等于逻辑上的否定;二是评价指标间的独立性问题。传统的基于效用的多属性决策方法中隐含的假设为线性可加性,该假设要求指标间必须独立,而在现实中指标间的相互独立是不可能的。上述两个问题降低了决策的合理性,因此,本文构建一套PPP项目方案决策模型,以提高PPP项目方案选择的合理性。
1 PPP项目方案选择评价指标体系
对于PPP项目方案的评价主要从经济性、有效性、社会效果、环境效果和能源资源效果五个方面来进行考察(见表1),原因如下:
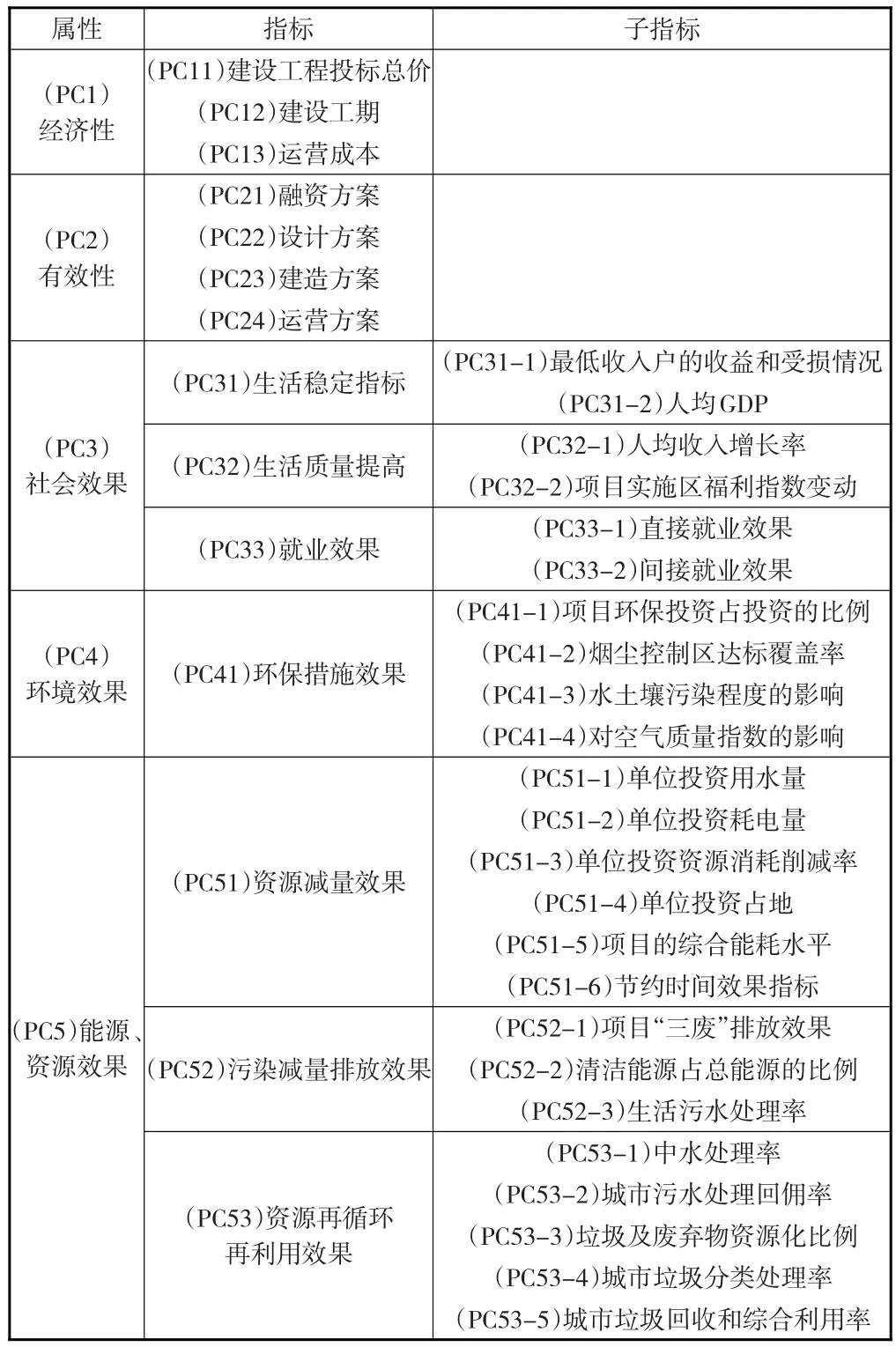
表1 PPP方案选择评价指标体系
(1)经济性。经济性主要是反映方案所需要的全寿命周期成本,直接影响PPP项目的融资方案与运营效果,主要包括建设工程投标总价和运营成本。此外,除直接经济因素外,工期的长短对于PPP项目的建设成本也有较大影响,需要考虑。
(2)有效性。有效性反映的是PPP项目方案的可执行性和满意度,主要通过融资、设计、建造和运营四个方面来考虑,从而提高PPP项目方案的公众满意度。
(3)社会效果。其评价指标包括:生活稳定指标、生活质量提高、就业效果。
(4)环境效果。公共项目的施工和运营必然会改变原有的生态环境面貌,对环境造成不可逆的破坏,因此需对方案的环保措施进行评价。
(5)能源、资源效果。大型公共项目的特点是投入大,所需要的能源和资源也必然巨大,因此在方案的选择中,需要选择能源、资源需求量较少的PPP项目方案。
2 PPP项目方案选择评价框架
对于PPP项目备选方案的评价共分为三个步骤,具体内容如下。
步骤1:确定评价指标和备选方案。
在确定PPP项目的目标后,将其目标进行分解,使其变成可被衡量的评价指标体系。具体可参考本文所提出的方案选择评价指标体系,具体指标可以根据实际情况进行修改。
在收到提供的方案后,根据所构建方案选择评价指标体系,将备选方案进行指标分解,以获取备选方案的评价值,而后采用优选法,对备选方案的评价值进行初选。
步骤2:确定指标的模糊测度。
模糊测度优点在文献综述已经说明,但是模糊测度的缺点也同样明显,那就是在应用模糊测度衡量指标的重要性时,不仅需要标出单个指标的重要性,还需要标出指标集的重要性,而这无疑增加了指标重要性赋值的难度。为了解决该问题,本文采用λ-模糊测度[4]来解决该问题。假设X是有限集合,则λ-模糊测度g满足公式(1):
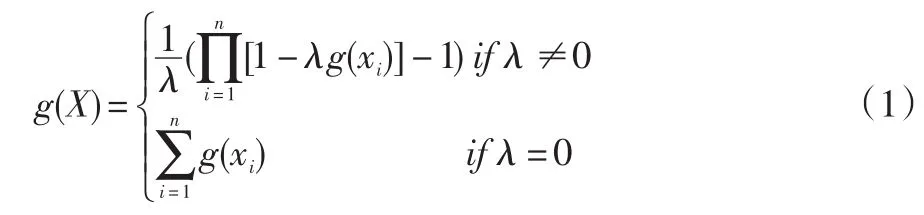
其中,xi⋂xj=ϕ,i,j=1,2,...,n,同时i≠j。对于单个指标xi∈X,g(xi)称为xi的模糊密度函数,表示属性的重要程度,可简记为gi=g(xi)。由公式(1)可知,对任意A∈P(X)有:
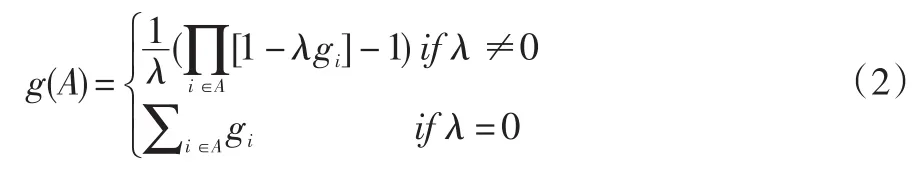
根据公式(1),当g(X)=1时,可由公式(2)确定λ:

基于上述的模糊测度的定义,评价属性、指标和子指标的模糊测度可以通过如下步骤获得:
(1)评价指标的重要性由专家根据方案的实际情况进行打分,分值区间为[0,1]。项目主管单位确定评价属性的重要性,指标间的相关作用关系由专家来确定。
(2)基于评价指标和属性的重要性评价值,通过公式(3)来确定参数λ,然后根据属性和指标的相互作用关系,通过公式(2)确定模糊测度。
步骤3:评价指标值集结。
在介绍框架之前,首先需要对直觉模糊数的相关概念进行说明。
定义1[3]:区间值直觉模糊集进行比较、排序,则借助于区间直觉模糊集的得分值和精确值得定义,(当区间值直觉模糊集只有一个元素x时,可以将它简记为可定义区间值直觉模糊集的得分值和精确值分别为:
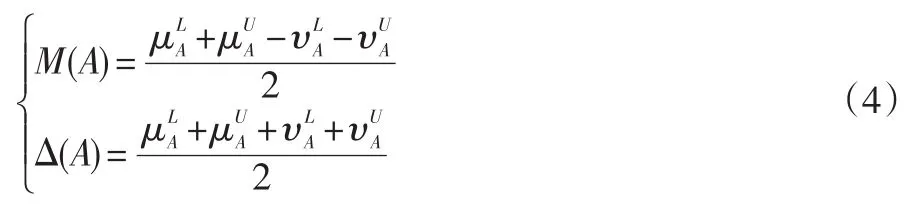
显然M(A)∈[-1,1],Δ(A)∈[-1,1]。于是,对两个区间直觉模糊集Aj和Ak,规定其如下:
如果M(Aj)>M(Ak),则Aj大于Ak,记做Aj>Ak;如果M(Aj)=M(Ak),则:(1)如果 Δ(Aj)=Δ(Ak),则Aj等于Ak,记做Aj=Ak;(2)如果 Δ(Aj)<Δ(Ak),则Aj小于Ak,记做Aj<Ak;(3)如果 Δ(Aj)>Δ(Ak),则Aj大于Ak,记做Aj>Ak。
命题1[3]:假设是一个1,2,...,n区间直觉模糊集合,μ是关于A={a1,a2,...,an}模糊测度,则区间直觉模糊Choquet集结算子(IVILCA)也可以被定义为:
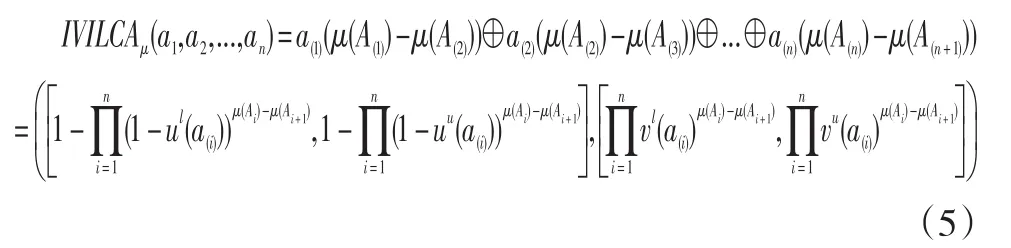
其中,(·)表示A上的一个转置,使得a(1)≤a(2)≤…≤a(n)且A(i)={a(i),...,a(n)},且A(n+1)=∅。
基于上述定义和公式,则PPP项目备选方案评价值集结步骤如下:
(1)将方案中的定量数据变为为区间直觉模糊数。通过公式(6)将定量数据转换为直觉模糊数:
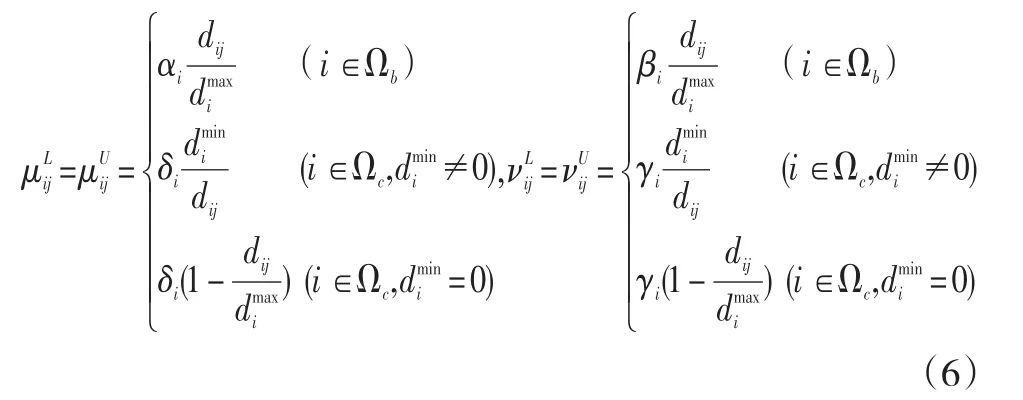
其中,α、δ为效益和成本指标的满意度参数,β、γ为效益和成本指标的不满意度参数。
(2)根据定性评价指标对PPP项目备选方案进行打分。专家首先通过在0到10之间打分来确定PPP备选方案在评价指标上的满意度区间[μL,μU],然后在从区间[0,1-μU]内对不满意度区间[υL,υU]进行打分。这两个分值构成了PPP备选方案在评价指标上的区间直觉模糊评估值。
(3)计算基于不同属性的PPP项目备选方案综合评价值。通过区间直觉模糊Choquet集结算子见公式(5),将不同备选方案的直觉模糊评价值和子指标、指标、属性的模糊测度进行集结,得到各备选方案的综合评价值,而后根据定义1,对PPP项目方案排序,并基于排序结果确定最优的方案。
3 实证检验
河南省某地进行拆迁改造工程,采用PPP模式,共提出了三个改造方案,为了保证PPP项目的顺利实行,本文应河南省人民政府PPP项目主管部门的要求对三个方案进行评选。
3.1 收集决策信息并确定评价指标体系
在对备选方案进行评价之前,需要确定方案的评价指标。由于三个方案在(PC31-1)、(PC31-2)、(PC41-3)、(PC41-4)、(PC52-2)、(PC53-2)、(PC53-4)和(PC53-5)指标上的评价值相同,为了减少评价的复杂度,因而删除上述指标。
专家首先对评价指标的满意度进行打分,分值为[μL,μU],取值区间为[0,1],而后专家在区间 [0 ,1-μU]内对方案的不满意度进行打分,分值为[υL,υU]。每个评价指标都有三个专家对其进行评价,在数据收集完成后,决策辅助人员需要分析专家评价的一致性,如果不同专家对于某个指标的同一个方案的评价不一样,则需要专家再次进行商议,直到达成统一的意见。由上述步骤获得PPP项目方案的定性评价指标数据,收集的数据见表2。
3.2 确定评价指标的模糊测度
在确定完评价指标之后,通过德尔菲法确定各个指标上的模糊测度,即从0到1的范围内,通过专家打分的方法,来确定每个指标的重要程度,结果见表3。
通过对表3进行分析,项目主管单位对于项目方案的环境效果更为关注,其次为经济性。这主要是因为国家对于环保越来越重视,因而地方单位在国家政策的引导下对于项目的环保问题更为关注;项目主管单位重视经济性的原因是PPP项目如果经济成本太高,则会给当地政府未来的财政带来过多的负担。因此如果方案在此方面评分较高,则被选中的机会较大。
3.3 综合各备选方案的评价信息
通过公式(6)将方案的定量评价数据转换为区间直觉模糊数,而后通过公式(5),将表2中的直觉模糊数和表3中的区间模糊测度进行集结。首先获得的是备选方案A1、A2和A3在各评价属性上的区间直觉模糊表现值,在经济性、有效性、社会效果、环境效果和能源、资源效果方面占优的分别是A3、A2、A3、A3和A1。而后再次通过公式(5)获得各备选方案总的评价值,基于评价属性和总体评价值见下页表4。
3.4 备选方案选择与分析
基于定义1,可知方案A3得分最高,因此以方案A3作为最终的方案,进行下一步的物有所值评价和社会资本选择。在各个方案的比较中可以发现,在经济性上,各方案的得分基本上较高,其中方案A3得到的评价最高;在有效性上每个方案的评价都不是很高,原因是棚户区改造施工毕竟会影响到居民的日常生活,而且对于方案来说,方案不能够满足所有人的需求,因此评价较低也是情有可原的。
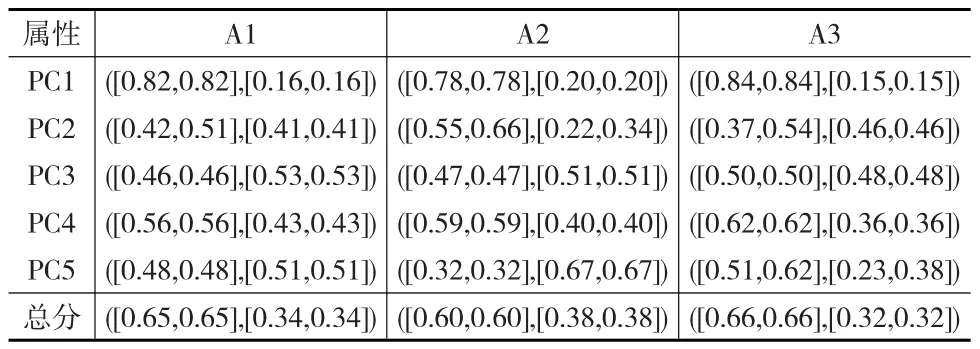
表4 各方案在各评价属性和总体上的评价值
4 总结
本文建立了PPP项目方案选择评价指标体系,主要从经济性、有效性、社会效果、环境效果和能源资源效果五个方面来对项目方案进行考察。构建了PPP项目方案选择评价框架,采用区间直觉模糊数代替实数,以减少信息的损失。而后采用模糊测度代替权重以表示评价指标的重要性,并基于区间直觉模糊Choquet积分算子构建基于直觉模糊集和模糊测度的多属性决策方法来实现PPP方案的最优选择。
然后通过实例检验了本文所提出模型的有效性。选取河南省某地拆迁改造工程实例,对该PPP项目三个备选方案进行评选,分析得出方案A3的评价最高。本文有效解决了项目方案决策时信息损失和评价指标间的独立性问题,极大地提高了决策的合理性和科学性,为项目决策者在方案选择上提供了有力的帮助。

