让等腰三角形教学更有几何味

刘东升

(江苏省海安市城南实验中学 226600)

中国教育学会中学数学教学专业委员会主办的全国初中青年数学教师优秀课展示活动是一项广受关注的全国性教学展评活动，近年来随着网络传媒技术的发展，使得该项活动能第一时间面向全国直播，我们足不出户，就能观摩学习到很多展示课及专家评析．在最近一次桂林召开的第十届初中青年数学教师优秀课展示活动中，我们对两节等腰三角形的展示课(分别是天津、青海两地选送)有些不同意见，整理出来，抛砖引玉，提供研讨．

1 青优展示课“等腰三角形(第1课时)”课例概述

说明：由于天津、青海两节课都是关于等腰三角形(第1课时)的教学展示，而且大同小异，限于篇幅下面只概述天津课例．

教学环节(一) 动手操作,引入课题

问题1：美丽的窗花是如何剪得的？

问题2：利用剪窗花的方法，我们再剪一个图案，你发现你手中的纸片是什么形状的？为什么？

教学环节(二) 实验操作，大胆猜想

问题3：将自己手中的等腰三角形纸片对折，观察重合的线段和角.你有什么发现？

预设追问：同学们手中的等腰三角形纸片是否具有这样的特点？

教学环节(三) 推理证明，归纳性质

问题4：利用实验操作的方法我们发现了与等腰三角形有关的猜想，请同学们验证这些结论是否正确.

预设追问：要证明两个角相等，你有什么方法？你是怎么想到构造全等的？(这个教学环节的课件截图如下)

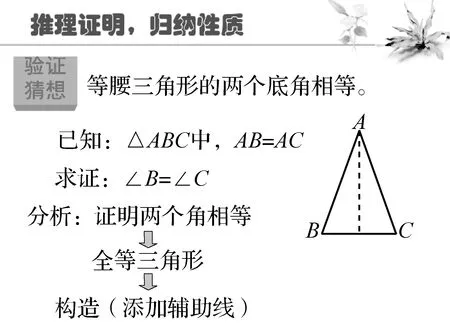
证明之后，形成板书，等腰三角形的性质1：等腰三角形的两底角相等(简写：等边对等角)并给出符号语言．

问题5：大家在证明过程中使用了不同的辅助线作法，它们有什么区别和联系？

成果扩大，板书出示等腰三角形的性质2：

等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.

简写成：三线合一．结合课件及板书引导学生总结符号语言．

教学环节(四) 巩固练习，熟悉性质

(一组常规的练习题，略)

教学环节(五) 性质应用，例题精讲

例：如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD.

(1)图中哪些三角形是等腰三角形？(追问：哪些角相等？)

(2)用含∠A的式子表示∠CDB、∠C、∠ABC.

(3)求出∠A的度数.

教学环节(六) 归纳小结，突出重点

小结：(1)经过这一节课的学习，我们学到了哪些主要内容？

(2)我们是如何探究等腰三角形的性质的？

(3)你学到了哪些证明线段相等或角相等的方法？

小结后，临下课前展示一组具天津地方特色图片，从图片中抽象出等腰三角形，并结合如何确定三角形是等腰三角形的问题引出下节课的学习内容.

【设计意图】通过具有天津地方特色的图片，引导学生从现实生活中抽象出几何图形的能力，感受家乡风景、建筑的美好，培养学生热爱家乡的情感，渗透德育教育，实现数学学科的育人功能；在此基础上结合教材编写及课堂教学的脉络，引导学生体会图形与几何领域“定义——性质——判定”的学习脉络.

2 评课与商榷

因为青优展示课是面向全国的高级别展评课活动，各省市都经过层层选拔、多级打磨、多次试教再推优到全国平台上来的，应该说，教学流程完整、语言规范等都是值得学习的．然而从深刻理解数学，理解平面几何教学，追求更有品质或深度的几何教学来看，我们提出如下评课商榷意见．

第一，辨识学段，别让操作实验的“生活味”冲淡了理性证明的“几何味”.

从教学流程及教学课件上的素材来看，这节课基本忠实于人教版教材，亦步亦趋，没有能从“教教材”走向“用教材教”的发展．比如，该课用了较多教学时间在折纸、剪纸等操作实验活动，这是一种学段特征辨识不清的教学行为．上述操作实验活动，学生在小学阶段已有相关的活动经验，而初中几何源自《几何原本》，离开操作实验(这些可以是低学段的数学活动)也可以有更显几何味的教学引入，比如:

开课阶段：黑板上渐次画出一般三角形、等腰三角形，定义两边相等的三角形为等腰三角形，并引导学生对比两个三角形，一般三角形与等腰三角形在边、角上有什么不同？等腰三角形特殊在哪儿？学生一定能发现“等腰三角形的两个底角相等”这一性质(在小学就已熟悉这个性质)，进一步引导证明命题“等边对等角”．

这样引入，开门见山，数学味、几何味极浓．用几何理性精神之趣味代替操作实验的活动之趣味，显然，这两种趣味截然不同．

第二，知易行难，“定义，性质，判定”的学习脉络没有得到很好的贯彻.

如我们在上面课例最后所引，课堂小结最后，选用了天津特色建筑的两幅图案，教者给出设计意图“培养学生抽象能力，感受家乡风景、建筑的美好，培养学生热爱家乡的情感，渗透德育教育，实现数学学科的育人功能”．这段乱贴标签式的意图解读莫名其妙，与本课等腰三角形的性质学习无甚关联，也与章建跃博士倡导“发挥数学的内部价值，实现数学的育人功能”相去甚远．教者选用两幅天津特色建筑的图案还有如下的设计意图，“在此基础上结合教材编写及课堂教学的脉络，引导学生体会图形与几何领域“定义——性质——判定”的学习脉络.”可见，教者知道几何研究的“基本套路”，然而从整节课的教学流程来看，却没有依据这样的“基本套路”来设计教学，知易行难，此亦一例．这里我们也可依据上述基本套路给出等腰三角形这个单元的教学路径(如下结构图，也可作为一种板书设计的结构图)．

就等腰三角形的第1课时来说，如果适当精减操作实验活动，开门见山，教学进度可以推进到等腰三角形的判定．这样作为一个单元教学的起始课，就可让学生在第1课时感受到等腰三角形这个单元的知识框架，至于例题习题的训练以及拓展到“大边对大角”内容，可以在后续习题课中教学跟进．

第三，聚焦细节，在两个课堂细节处看教学难点的理解仍然有待深入.

细节之一：证明命题“等边对等角”的真正难点在哪儿？

从教师的教学过程以及相关点评稿的研读发现，展示团队都把本课的教学难点定位在等腰三角形的性质证明．然而突破这一教学难点时，两节课都忽略了一个教学细节的处理．这就是证明命题“等边对等角”时，对该文字命题转化为符号表达的“已知、求证”这一环节都是“一带而过”，以课件直接呈现“已知，求证”，“帮助”学生快速进入添加辅助线证明全等．在笔者看来，添加辅助线证明对于多数学生并不是难点，因为前面一章训练全等三角形时，学生已有很多类似的证明经验，根据教学经验，构造全等证出对应角相等并不是本节课的教学难点．而与添加辅助线证出“等边对等角”相比，引导学生辨别“等边对等角”这个命题的题设与结论更加重要，即被教师“一带而过”的“已知，求证”环节，可以设计如下：

师：现在我们来证明命题“等腰三角形的两个底角相等”，同学思考一下，这个命题的题设是什么？结论是什么？你们能画图，写出已知、求证吗？

预设：题设是三角形的两边相等，结论是这两条边所对的角相等．在此基础上引导学生画图，结合等腰三角形定义的符号表达，自主写出已知与求证．也就是说，学生将文字命题向图形、符号语言转译的过程中，明辩题设与结论是更加重要的．

细节之二：例题教学时的设问显示教师命题基本功还有待修炼.

例题教学时，选用的是教材上的那道经典的“黄金三角形”(顶角为36°的等腰三角形)，教材例题如下：

在△ABC中，AB=AC，点D在边AC上，且BD=BC=AD.求△ABC各个内角的度数．

而教师处理该例题时，重新设问3个，前两个可看作是铺垫式问题，但设问可以进行如下的打磨：

(2)设∠A=α，用含α的式子表示∠CDB、∠C、∠ABC；

(3)求三角形ABC的各个内角的度数．

说明：第(2)问为了让学生表述更加简洁，第(3)问也应该“成果扩大”，让学生求出“黄金三角形”的各个内角度数．

进一步，如果熟悉数学命题改编的一些常用技术，将条件与结论恰当置换，可以由这个经典的“黄金三角形”问题，逆向设问，引出“等角对等边”的内容，改编如下：

在△ABC中，∠A=36°，∠ABC=72°，BD是△ABC的角平分线．这个图形中有几个等腰三角形？

教学预设：学生根据三角形内角和很快就能求出其它角度，也很快能发现三个等腰三角形，但是证明时却要用到“等角对等边”，如果时间足够，就可将问题抽象出来，继续研究，如果教学时间不够，也可用这个“遗留问题”进行“生长式小结”，并作为下一节课开课的数学情境．

3 结束语

等腰三角形起始课教学一直是各级教学研讨的热点课题，教无定法，背后也体现着教师的数学理解与教学观，我们的商榷意见也只是基于个人兴趣和喜好以“同课异构”的方式提出来的，虽然在自身的教学中进行过实践，也不一定准确，更不一定正确，供大家批评指正．