腹板纵向加劲肋对移动模架主梁屈曲稳定性的影响

苏胜丰

(中交二航局第四工程有限公司，安徽 芜湖 241000)

0 引 言

移动模架是一种配备液压电气系统、机械化程度较高的桥梁原位现浇施工设备。根据设备结构布置方式，可分为上行式移动模架和下行式移动模架，根据行走方式可分为牛腿自行式移动模架和非自行式移动模架[1-3]。

目前，国内外对于移动模架的研究主要集中在移动模架施工工艺、结构计算等领域，对移动模架主梁屈曲稳定性的研究较少。欧阳博涵[4]、程晔[5]、谢瑾荣[6]、张启贵[7]等分别针对特定型号架桥机主梁进行了静强度及局部屈曲稳定性计算，得出了特定截面尺寸下架桥机主梁的极限承载力，但未对不同截面架桥机主梁屈曲稳定性变化规律进行对比研究。石志响针对多种尺寸箱型截面柱在轴压载荷作用下的残余应力、屈曲稳定性进行了研究，得出了箱型截面柱的残余应力及分布形态，同时对高强钢箱型截面柱在轴压作用下的临界宽厚比限值提出了建议取值，但未就内部筋板对箱梁截面柱屈曲稳定性的影响进行研究[8]。安超对特定型号移动模架在不同工况下的屈曲稳定性进行了研究，得出了不同工况下移动模架极限承载力，但未对移动模架筋板对极限承载力的影响进行研究[9]。梁嘉就纯剪切状态下腹板开孔孔径大小对极限承载力的影响进行了研究，得知开孔腹板极限承载力随开孔距高比及孔高比的变化而变化[10]。雷海鹏就槽钢肋矩形加劲板在侧压力及轴向载荷作用下的失稳模态及极限承载力进行了研究，建立了单根槽钢肋加劲板弯扭屈曲方程，但未对不同位置下槽钢加劲肋对矩形板极限承载力的影响进行研究[11]。移动模架主梁屈曲稳定性主要由截面的几何性质决定，同时腹板纵向加劲肋的位置及几何性质也会对主梁屈曲稳定性产生显著影响，而移动模架屈曲稳定性将直接影响移动模架主梁的承载力。

因此，本文将常用移动模架主梁截面作为研究对象，通过对移动模架主梁腹板纵向加劲肋的位置进行细化分析，研究在相同边界条件下腹板纵向加劲肋位置对主梁屈曲稳定性的影响，为移动模架设计提供参考。

1 移动模架主梁截面选取及参数设置

移动模架虽然型号较多，但是结构组成基本相同，均由主梁、鼻梁、横梁、台车、牛腿、内外模板及液压机电系统组成(图1)。主梁是移动模架的主要受力构件，其最大跨度达60 m，最大载荷达4 000 t。目前国内常用移动模架规格型号以30 m和50 m跨径居多，选取5种常用截面作为计算对象。类型1尺寸为1.5 m×2.0 m；类型2为1.5 m×2.3 m；类型3为1.5 m×2.5 m；类型4为1.5 m×2.7 m；类型5为1.5 m×3.0 m。截面布置如图2所示，图中各参数的取值见表1。

图1 移动模架

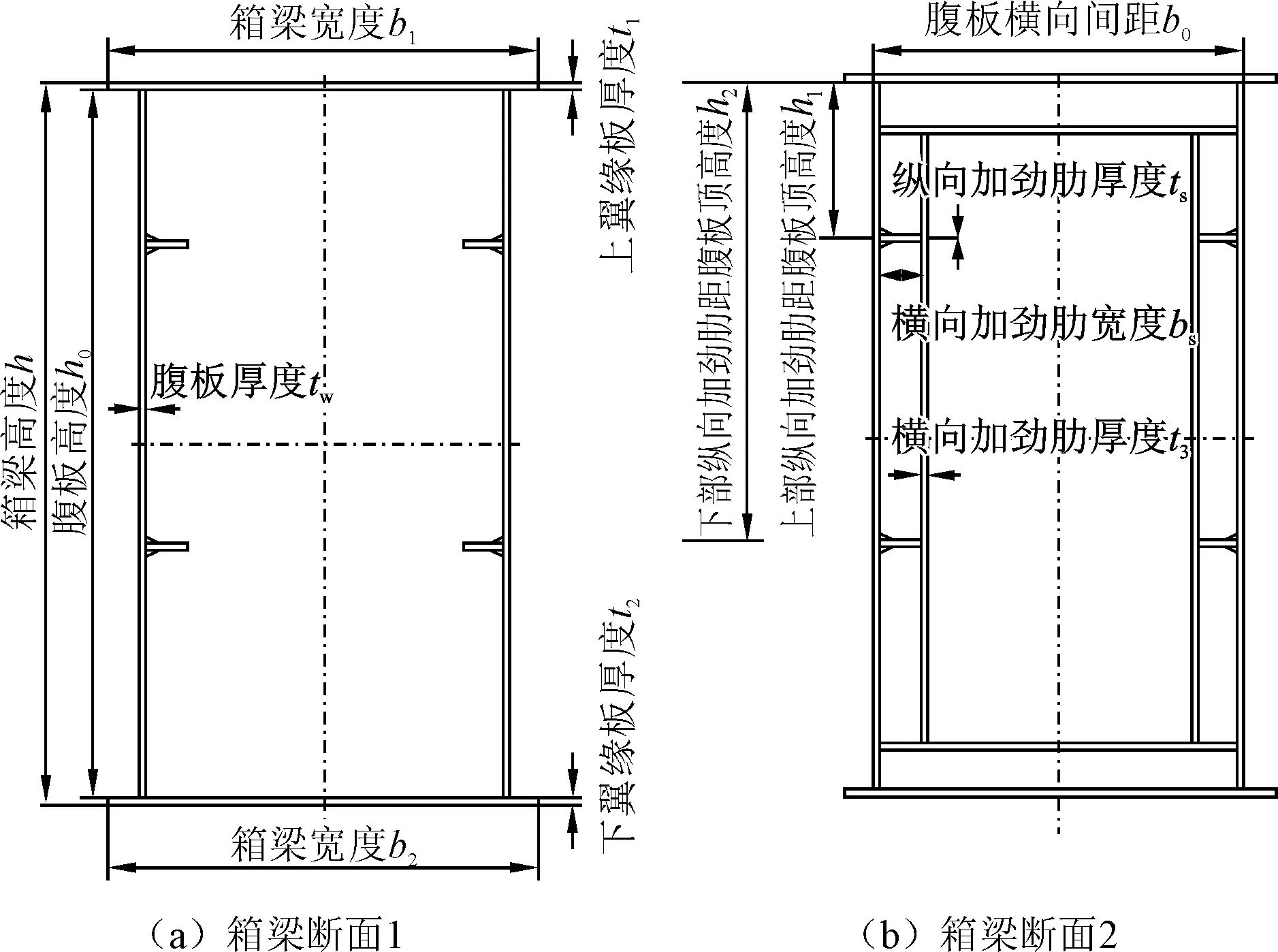
图2 截面布置

1.1 移动模架主梁整体稳定性计算

根据《钢结构设计规范》(GB50017—2017)可知：箱型截面满足以下要求时，可不计算整体稳定性。

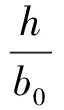
(1)

(2)

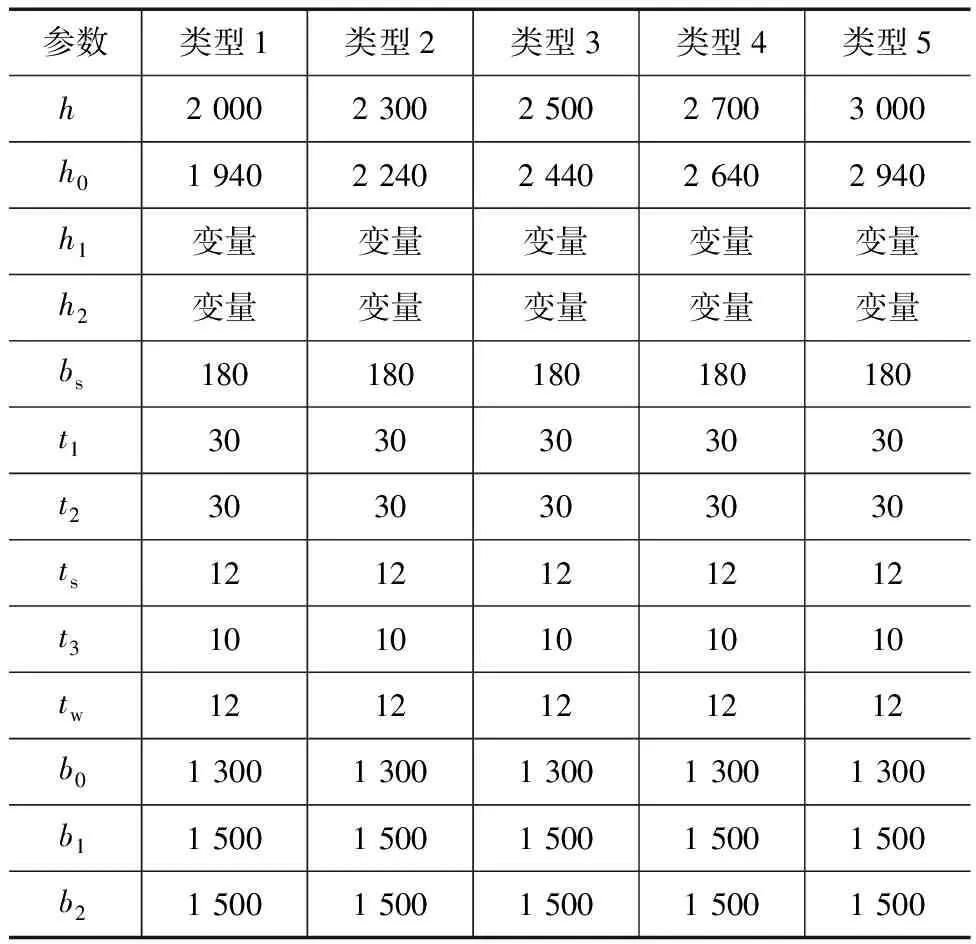
表1 移动模架主梁截面参数 mm

式中：l1为箱梁计算长度；f为材料屈服强度。

5种截面整体稳定性的计算值及理论值对比见表2。

表2 移动模架主梁整体稳定性计算结果

通过表2可以看出，5种类型移动模架主梁的高宽比、长宽比均满足规范要求，无需计算整体稳定性。由此说明移动模架主梁型号选取正确，不会因整体稳定性不足影响纵向加劲肋对主梁屈曲稳定性的后续分析。

1.2 移动模架主梁横、纵向加劲肋局部稳定性计算

根据《钢结构设计规范》(GB 50017—2017)的规定：横向加劲肋的最小间距应为0.5h0，最大间距为2h0，模型取值为2.0 m，满足规范要求。同时规范要求：在腹板一侧配置的横向加劲肋，其外伸宽度应大于腹板两侧布置横向加劲肋宽度的1.2倍，厚度应不小于其外伸宽度的1/15。根据腹板两侧成对布置的横向加劲肋计算公式，外伸宽度和厚度为

式中：bs为外伸宽度；ts为厚度。

5种截面计算模型横向加劲肋的外伸宽度、厚度与规范要求值的对比见表3。

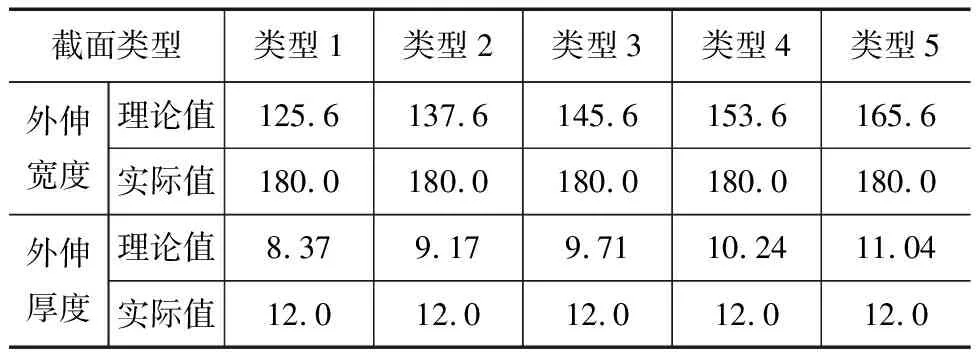
表3 横向加劲肋外伸宽度及厚度计算结果 mm

由表3可以看出，5种截面的移动模架横向加劲肋的外伸宽度及厚度均满足规范的稳定性要求，不会因横向加劲肋的局部失稳而影响纵向加劲肋对主梁的屈曲的稳定性。

在同时采用横向加劲肋和纵向加劲肋的加强腹板中，横向加劲肋的截面尺寸不仅应符合表2的要求，其截面惯性矩Iz还应符合下式要求。

(5)

计算对比结果见表4。

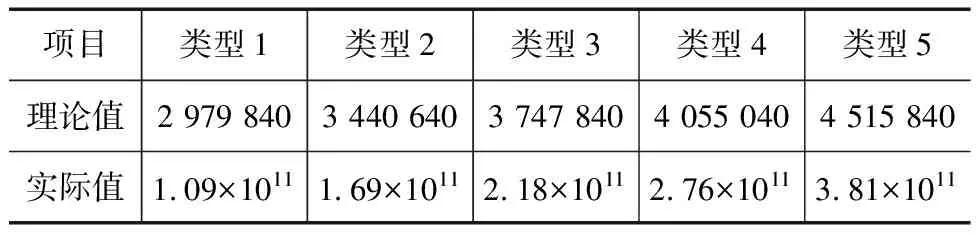
表4 横向加劲肋截面惯性矩计算结果 mm4

由表4可以看出，5种型号移动模架主梁横向加劲肋相对于腹板的截面惯性矩满足规范稳定性要求，不会先于腹板或纵向加劲肋发生局部失稳，满足继续分析纵向加劲肋对主梁屈曲稳定性的要求。

2 腹板纵筋位置对主梁稳定性的影响

由表2～4可以看出，当移动模架主梁各参数按表2进行赋值时，移动模架整体稳定性、局部稳定性均满足规范要求。但根据《钢结构设计规范》(GB 50017—2017)的规定，受弯构件腹板纵向加劲肋应布置在0.2h0～0.25h0内。

本文利用有限元数值分析软件，对腹板纵向加劲肋位置在0.1h0～0.4h0进行赋值，从而分析移动模架主梁腹板稳定性的变化情况。有限元模型采用Shell63单元进行模拟，共划分板壳单元5 638个，节点6 792个，有限元数值分析计算模型纵向长度L1=52.0 m，支点间距L2=50 m，左侧支点约束UX、UY、UZ三个方向位移自由度，右侧支点约束UX、UY两个方向位移自由度，释放UZ方向位移自由度，其中坐标轴Z方向为沿主梁长度，X方向为沿主梁横向宽度，Y方向为沿主梁竖向高度。因移动模架主梁弹性屈曲稳定性仅与截面特性有关，与载荷大小无关，故有限元数值分析中根据移动模架实际加载位置，在每个加载点施加单位荷载，单根主梁共20个作用点，荷载F=20 N，如图3所示，有限元计算模型见图4。根据数值分析计算结果，移动模架主梁屈曲稳定性特征值随腹板纵向加劲肋位置的变化规律见图5，主梁失稳变形见图6，局部放大见图7，失稳变形位置主要集中在主梁跨中上腹板，即主梁跨中腹板受压区域。

图4 有限元计算模型

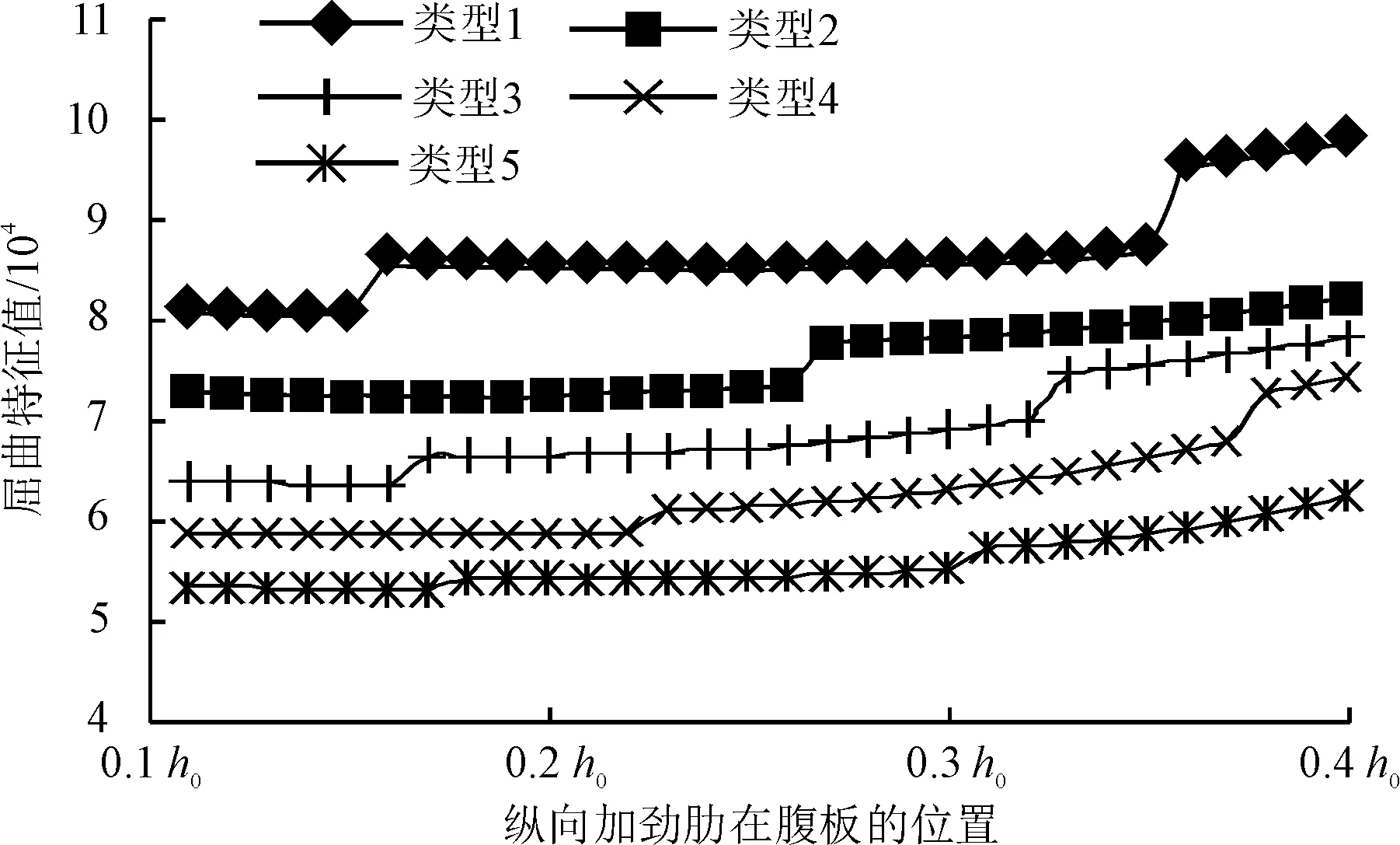
图5 移动模架主梁稳定性特征值随腹板纵向加劲力位置的变化规律

图6 移动模架主梁失稳变形

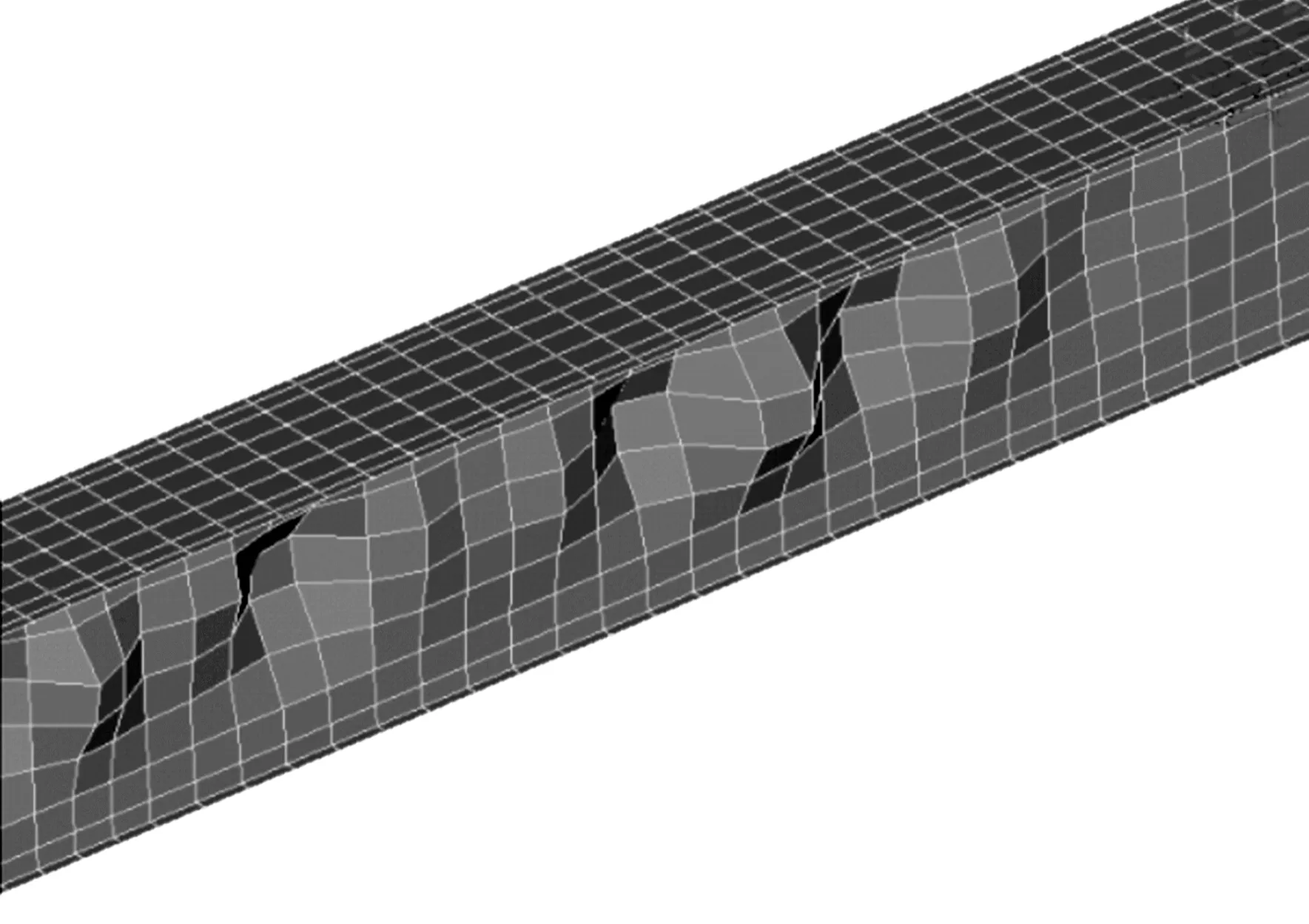
图7 主梁失稳变形放大

图3 计算简图

由图5可以看出：以移动模架主梁屈曲稳定性特征值作为计算模型单位载荷的放大倍数，直接反映了移动模架主梁的承载能力；该特征值随腹板纵向加劲肋位置的变化而线性变化，并在0.25h0～0.35h0明显增大，增大比例达5.8%～9.7%。

因此，建议在主梁刚度满足要求的前提下，可以适当降低腹板纵向加劲肋的竖向位置，控制在0.25h0～0.35h0，这样可显著提高主梁屈曲稳定性。由图6、7可以看出，主梁的失稳变形位置主要发生于腹板纵向加劲肋与翼缘板之间的腹板受压区，并以横向加劲肋为侧向支撑点，呈正弦波方式布置。

3 结 语

利用有限元分析软件，模拟研究移动模架主梁腹板纵向加劲肋竖向位置对主梁屈曲稳定性的影响，得到以下结论。

(1)在截面特性、横向加劲肋布置间距、外伸宽度及厚度均满足局部稳定性及整体稳定性的前提下，腹板纵向加劲肋竖向位置在0.25h0～0.35h0时，主梁屈曲稳定性特征值可提高5.8%～9.7%。

(2)移动模架主梁屈曲稳定性特征值随腹板纵向加劲肋位置的变化而变化，失稳变形位置主要集中在主梁跨中上腹板，即主梁跨中腹板受压区域。

(3)主梁的失稳变形位置主要发生于腹板纵向加劲肋与翼缘板之间的腹板受压区，并以横向加劲肋为侧向支撑点，呈正弦波方式布置。