扁平箱梁的颤振临界风速估算

文 锋，郑晓东，张 辉

(1.长安大学 公路学院，陕西 西安 710064；2.中交公路规划设计院有限公司 ，北京 100088)

0 引 言

随着桥梁的跨度不断增加，以及新材料和自动化施工技术的应用，使得桥梁结构阻尼越来越低。因此，桥梁在风的作用下越来越敏感，风荷载已经成为控制大跨度桥梁施工和运营安全的关键因素之一。在各种风致桥梁振动效应中，颤振是最具危险性的发散性振动现象，需要在设计阶段通过采取适当的抗风措施杜绝颤振的发生。

关于桥梁颤振稳定性的判定，Theodorsen根据机翼颤振分析理论提出了平板颤振理论，但在用平板颤振理论分析Tacoma桥的颤振临界风速时，发现理论与实际情况并不相符。所以，Bleich将断面两侧漩涡给加劲梁断面带来的升力矩和附加升力的影响考虑进Theodorsen平板颤振理论，用修正后的理论计算出的颤振临界风速与实际桥梁发生颤振时的风速比较接近。Klöppel和Thiele为了完善该分析方法，提出了一套计算程序，专门用来分析Bleich悬索桥的颤振稳定性，并将结果绘制成了适用于悬索桥分析的诺模图，用诺模图可以直接求解悬索桥颤振临界风速。Van der put在Klöppel/Thiele的诺模图基础上，运用数理统计的方法，拟合出了理想薄平板颤振临界风速的实用公式。Chen[1]基于桥梁气弹模型的多模态耦合响应，给出了颤振临界风速计算的解析公式。Gianni Bartoli[2]对颤振稳定性的评价做了大量的研究，提出了只需借助3个甚至2个气动导数的桥梁颤振评价方法。

中国学者项海帆等[3]开展了相关研究，讨论了大跨桥梁2种颤振理论的临界风速实用计算公式，并给出了一个统一表达形式的临界风速近似估算公式，以及一个大跨桥梁颤振稳定性的简化判据公式。葛耀君等[4]基于结构的可靠性理论，通过极限状态方程建立了桥梁颤振的可靠性分析模型，并提出了用以确定桥梁颤振稳定失效概率的计算方法。白桦 等[5-6]基于频域分析法分析振动方程中的单元气动阻尼矩阵与气动刚度矩阵及弯扭耦合颤振驱动机理，将借助颤振导数研究颤振失稳问题转化为借助三分力系数研究颤振失稳，给出了基于三分力系数的颤振稳定性快速评价参数F。刘乐[7]通过静三分力系数和颤振稳定性的定性关系、宽高比和颤振稳定性之间的关系，借助最小二乘法，拟合出评价悬索桥在3°、0°风攻角下颤振稳定性的参数L。

虽然国内外学者对颤振稳定性做了大量的研究，并使桥梁颤振理论和评价标准逐渐完善，但目前国内抗风规范以及研究对桥梁颤振临界风速的估算公式都是基于理想薄平板，即通过分析相应薄平板的参数变化对颤振临界风速的影响，归纳出薄平板颤振临界风速计算公式，再考虑桥梁断面的形状系数、攻角系数和桥梁体系，将薄平板颤振临界风速转化成实际桥梁的颤振临界风速。尽管这样的计算过程节省了大量的资源，不需借助风洞试验或者CFD数值模拟手段，较其他评价准则简便，但由于对影响系数的考虑不够全面，以及颤振稳定性的敏感性并未完全体现，所以评价结果并不能完全反应实际桥梁断面颤振稳定性。本文旨在提出一种新的大跨径桥梁扁平箱梁断面颤振临界风速估算的方法，方便前期方案比选和满足相关科研的需要。

1 扁平箱梁颤振临界风速实用公式拟合

在分析斜拉桥和悬索桥颤振稳定性时，需要考虑动力特性、几何特性、气动外形、偏心质量、阻尼及偏心距的影响，另外桥塔和缆索体系也会对颤振临界风速产生影响。这些影响因素被分成两大类：一是主梁断面的气动外形，如主梁断面的宽高比、斜腹板的角度、栏杆的透风率等；另一类是桥梁的动力特性，如质量和频率等。

1.1 影响颤振稳定性的主要因素

采用Scanlan提出的经典计算方法，分别计算扁平箱梁断面在不同的质量、质量惯矩(I)、阻尼比以及扭弯频率工况下的颤振临界风速，用以研究不同的质量(m)、质量惯矩、阻尼比和扭弯频率与颤振临界风速关系。计算结果如图1所示。各参数变化会引起颤振临界风速V的变化，V变化后与变化前的比值用RV表示，可以将其称为益损系数。RV>1表示参数变化后，颤振临界风速V提高；RV<1表示颤振临界风速V降低。RD是参数变化后与变化前的比值，当RD>1表示参数提高，RD<1表示参数降低。

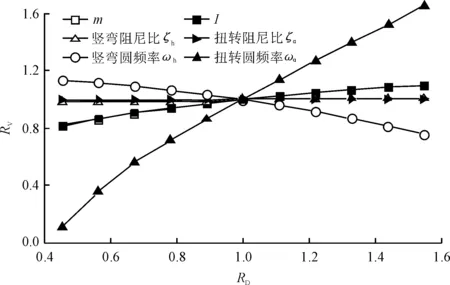
图1 各参数对颤振临界风速的影响

从图1中可以看出：扭转圆频率对扁平箱梁颤振临界风速的影响最大，随着扭转圆频率的增大，颤振临界风速也增大；竖弯圆频率对颤振临界风速的影响仅次于扭转圆频率，但颤振临界风速随竖弯圆频率的增加而减小；断面质量与质量惯矩对颤振临界风速的影响几乎相同，即随着质量和质量惯矩的增加，颤振临界风速也增大；阻尼比对颤振临界风速的影响最小，且实际工程中扁平箱梁基本为钢箱梁，所以在计算时阻尼比取千分之五。

1.2 拟合实用公式

本节主要考虑质量、质量惯矩以及扭弯频率对颤振稳定性的影响。目前，对桥梁颤振临界风速公式拟合的研究大多以Selberg公式或者Van der Put公式为数学模型，前者是由一系列试验的结果推导而来，后者则基于气动力的精确表达式算出的无量纲参数的诺模图，继而拟合成近似的直线表达式，具有较高的精度，且对颤振临界风速的影响因素考虑较全面，所以本文选取Van der Put公式为数学模型，将常数参数化后为

(1)

式中：Vcr为颤振风速；β1、β2、β3、β4、β5为待定参数；扭弯频率比ε=fα/fb，fα、fb分别为扭转频率、竖弯频率；μ=m/2πρb2，ρ为空气密度，b为半桥宽；r为惯性半径。

将式(1)右侧移项为

(2)

该公式左右两侧都是无量纲数，方便进行规律的探讨与公式拟合。此外，可采用分阶段拟合顺序，即先根据扭弯频率比与折减风速的关系求出β1、β2，再由最小二乘法求出β3、β4、β5，最后得出拟合结果。

由不同的μ与r/b工况下Scanlan经典计算方法得到的数据，进行一次线性拟合计算得到12组ε与Vcr/fbb的诺模图，如图2所示。

图2 不同工况下ε与Vcr/fbb 关系

不同μ与r/b工况下ε与Vcr/fbb的关系拟合线近似交于一点，表明扭弯频率比和折减风速呈线性关系，即存在常参数β1、β2使ε=β1时，Vcr/fbb=β2。从图中还可以看出，多条直线的交点就是参数β1、β2的值，即(β2，β1)=(0.690 0，3.860 1)，这里交点取所有直线交点的平均值，代入式(2)得

(3)

将式(3)常数项与(ε-0.690 0)移至公式左侧得

(4)

(5)

将式(5)化简得到

(6)

其中

(7)

将式(6)两侧取对数

f(x1,x2)=lnα1+α2lnm+α3lnI

(8)

则待拟合参数的公式为

f(x1,x2)=γ1+γ2·x(m) +γ3·x(I)

(9)

为得到最小二乘拟合方法需要的数据，只改变主梁断面的质量和质量惯矩，利用Scanlan提出的颤振临界风速计算方法，得到不同的颤振临界风速。其中因变量m⊂[9.138 9，21.138 9]，梯度为1，因变量I⊂[0.353 4，0.703 4]，梯度为0.05。将计算数据利用MATLAB编制最小二乘法计算程序，得到[β3、β4、β5]=[6.250 2，0.601 5，0.640 8]，代入式(1)得

(10)

2 CFD数值模拟修正公式

扁平箱梁的颤振临界风速是各种因素综合作用的结果，其中主要影响因素是主梁断面气动外形与桥梁动力特性，所以仅考虑桥梁动力特性的变化对颤振临界风速的影响，而忽略桥梁断面气动外形对颤振临界风速的影响，无法保证拟合公式的精度；而在风洞实验室中考虑主梁断面气动外形对颤振临界风速的影响，成本较大。所以，本文采用CFD数值模拟技术修正实用公式。

2.1 CFD数值模拟精度参数设置

采用ICEM软件生成断面周围的网格，并进行边界设置，全流场的长度为主梁断面桥宽的30倍左右，全流场的宽度为截面梁高的20倍以上，桥梁断面的形心位于距离风速入口流场处，网格选用适用于流固耦合的动网格——三角形网格，如图3所示。速度入口、速度出口、上下边界、流场名称以及截面刚体名称如图4所示。采用Fluent为求解器，湍流模型选用标准的k-ω湍流模型，残差设置为0.000 1，时间步设置为瞬态步，每步间隔为0.01 s。在识别桥梁断面的气动导数时，常规的Fluent参数设置并不能满足要求，需要在Fluent中嵌入纽马克方程的UDF(用户自定义函数)程序以驱动动网格来实现自由耦合振动法识别桥梁颤振导数[8-9]。

图3 网格划分

图4 计算模型及边界条件

利用CFD数值模拟估算了棋盘洲长江公路大桥原方案成桥状态下0°、3°和5°风攻角的颤振临界风速，CFD数值模拟结果分别为64.95、55.58、50.27 m·s-1，风洞试验颤振临界风速分别为64.04、52.60、45.74 m·s-1。CFD数值模拟精度较高，误差从1.42%(原方案成桥状态0°攻角)到9.90%(原方案成桥状态5°攻角)不等，且风攻角越接近0°，精度越高。本文修正计算公式只需计算0°风攻角下的颤振临界风速，所以精度满足要求。

2.2 气动外形对颤振临界风速的影响

由于拟合估算颤振临界风速所使用的对象是扁平箱梁，并不需要考虑桥梁运营阶段主梁断面的附属设施对颤振临界风速的影响[10-12]，而对于这种扁平箱梁断面，影响气动外形的因素并不多，若精确地考虑扁平箱梁断面的每处细节，费时耗力，且结果并不一定理想，所以本文选取对桥梁气动外形影响较大的2个参数：宽高比(B/H)和斜腹板倾角α。

2.2.1 宽高比与颤振临界风速的关系

扁平箱梁的宽高比变化较大，其中桥梁断面的宽度在30～50 m之间，高度在2～5 m之间。为尽量减少CFD数值模拟的工作量，假设不同斜腹板角度的颤振临界风速成一定比例关系，保持斜腹板角度15°不变，可以分别计算宽高比为8、9、10、11、13、14、15、16时断面的气动导数，将所有计算工况的主梁断面高度定为4 m，继而估算出颤振临界风速，结果如图5所示。

图5 不同宽高比断面的颤振临界风速

由图5可以看出，颤振临界风速随着断面宽高比的增大而减小，且基本呈线性关系；当宽高比低于8或者高于16时，宽高比的变化对颤振临界风速的影响变小。

通过不同宽高比断面的颤振临界风速的计算发现，宽高比的变化对桥梁颤振临界风速的影响较大，所以颤振临界风速计算的实用公式应该修正断面宽高比的影响。将图5中的数据进行一次线性拟合，得到颤振临界风速与主梁断面宽高比的函数关系为

RV=2.039 3-0.084 7B/H

(11)

则考虑宽高比的影响后，得到的修正公式为

(12)

2.2.2 斜腹板倾角与颤振临界风速的关系

保持断面的宽高比为11、12、13，分别计算斜腹板角度为14°、15°、16°、17°、18°断面的气动导数，然后估算出颤振临界风速，结果如图6所示。

图6 不同斜腹板角度断面的颤振临界风速

由图6可知，斜腹板角度对断面颤振临界风速有一定影响，并且随着斜腹板倾角变大，主梁断面颤振临界风速变小，但斜腹板倾角为14°～18°时，颤振临界风速相差基本在10%以内，与主梁断面宽高比对颤振临界风速的影响相比，斜腹板倾角对颤振临界风速的影响较小。实际桥梁断面的斜腹板角度大多集中在14°～17°，在此范围外的扁平箱梁较少建设，所以本文颤振临界风速计算公式的修正不考虑斜腹板倾角的影响。

3 工程应用

采用长江三桥、润扬长江大桥、南京四桥、虎门大桥、大沙水道桥、厦漳跨海大桥、南京二桥以及苏通大桥的风洞试验所测得的颤振临界风速为标准，按照规范给定的3种计算公式和本文拟合出来的公式分别计算各个桥梁的颤振临界风速及误差，结果如表1所示。

Van der Put公式计算的实桥颤振临界风速误差最小为1.37%，误差最大为26.91%；Selberg公式计算结果的离散性较大，误差最小为9.88%，但是误差最大为65.74%；同济大学公式稳定性较好，误差在10%～30%；本文拟合出来的计算公式误差在20%以下，最大误差为17.59%，最小误差为1.23%。

表1 误差比较

由长江三桥、南京四桥、虎门大桥、南京二桥以及厦漳跨海大桥的颤振临界风速估算结果来看，Selberg公式与同济大学公式计算的误差较大，而Van der Put公式和本文公式计算的误差较小；润扬长江大桥的颤振临界风速估算中，4个公式计算的误差都比较大，其中Van der Put公式误差为26.91%，Selberg公式为25.33%，同济大学公式为27.52%，本文公式为17.59%；本文公式估算的大沙水道桥的颤振临界风速误差最小，为1.23%，其余公式估算的结果误差较大；苏通大桥的颤振临界风速估算中，同济大学公式估算的结果误差较大，其余公式估算的结果误差均较小。

4 结 语

(1)分析了影响扁平箱梁颤振稳定性的影响因素，其中质量、质量惯矩、扭弯频率对颤振临界风速影响较大，确定Van der Put公式为本章公式的数学模型。

(2)利用弯扭频率比与折减风速的线性关系，结合最小二乘法初步拟合出扁平箱梁的颤振临界风速计算公式，利用CFD数值模拟技术考虑了桥梁断面宽高比和斜腹板倾角对颤振临界风速的影响，用主梁断面宽高比对颤振临界风速的影响修正初步拟合的公式。

(3)结合长江三桥、润扬长江大桥、南京四桥、虎门大桥、大沙水道桥、厦漳跨海大桥、南京二桥以及苏通大桥的风洞试验结果对本文计算公式和抗风规范提供的公式进行了比较，得出本文拟合的公式计算精度较高。