圆锥曲线创新题型及应对策略

■河南省项城市第一高级中学 王 璞

圆锥曲线内容是平面解析几何的核心内容,因而是高考重点考查的内容。随着课程改革的深入和推进,高考改革从知识立意转向能力立意,推出了一批新颖、别致、具有创新意识和创新思维的新题。考虑2019年高考趋势,会继续坚持注重基本知识和通性通法的考查。本文针对圆锥曲线中的部分创新题型进行分类赏析,以探索题型规律、揭示解题方法。

一、离心率求值或范围问题

图1

方法一:在黄金双曲线中,|O A|=a,|O B|=b,|O F|=c。

|B F|2+|A B|2=|A F|2,所以b2+c2+c2=a2+c2+2a c,因为b2=c2-a2,整理得c2-a2-a c=0,所以e2-e-1=0,解得e=(舍去),故黄金双曲线的离心率

图2

设“黄金双曲线”方程为0,b＞0),则B(0,b),F(-c,0),A(a,0),因 为所以-a c+b2=0。因为b2=c2-a2,所以c2-a2-a c=0,所以e2-e-1=0,解得(舍去)。故选A。

点评:解决圆锥曲线与向量相结合的问题,应先看能不能使用坐标法,把几何性问题转化成代数问题再进行解决。

例2双曲线的两个焦点分别为F1,F2,P是其上的点,且|P F1|=2|P F2|,则双曲线离心率的取值范围是( )。

A.(1,3) B.(1,3]

C.(3,+∞) D.[3,+∞)

解法一：利用余弦定理及三角函数的有界性求解。

设|P F2|=m,∠F1P F2=θ(0＜θ≤π)。

因为-1≤cosθ≤1,e＞1,所以e∈(1,3]。

解法二：利用三角形的性质。

不妨设|P F2|=m,则|P F1|=2m,由双曲线的定义可得|P F1|-|P F2|=2a,所以|P F2|=2a,|P F1|=4a。

在△P F1F2中,2a+4a＞2c,4a-2a＜2c,所以

又当P,F1,F2三点共线时,2a+4a=

点评:解法一根据双曲线的定义结合余弦定理将离心率转化为角的函数,再利用三角函数的有界性求出函数最值;解法二利用三角形的任意两边之差小于第三边的性质求解,简单易行。

二、弦长问题

例3已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N,若M为FN的中点,则|FN|=

解法一：易得,Mx=,所以

如图3,M(1,22),所以N(0,42),所以|FN|=

图3

解法二：易得

点评:本例难度系数较低,注意题中条件“若M为FN的中点”,解题时一定会用到中点坐标公式。

三、轨迹方程问题

例4过原点作直线l和抛物线y=x2-4x+6交于A,B两点,求线段A B的中点M的轨迹方程。

解析：由题可知,直线l的斜率一定存在,设直线l的方程为y=k x,代入抛物线方程得x2-(4+k)x+6=0,由Δ＞0,解得

设A(x1,y1),B(x2,y2),M(x,y),则或x＞6。

规律总结：求轨迹方程的常用方法:①直接法;②相关点法;③参数法;④定义法。

注意事项：①求轨迹方程的关键是在复杂的运动变化中,发现动点的运动规律,即动点满足的等量关系。要学会动中找静,变中求不变。②轨迹方程可用普通方程F(x,y=0表示,也可以用x=f(t),(t为参数)来｛y=g(t)表示,若要求轨迹方程,需把参数方程化成普通方程。③求出轨迹方程后,应注意检验是否满足题意。

四、对称问题

例5已知椭圆上两个不同的点A,B关于直线对称。求实数m的取值范围。

解法一：利用判别式及韦达定理来求解。

设A(x1,y1),B(x2,y2)。

点评:使用判别式及韦达定理这种方法来求解时,必须抓住:①垂直;②平分;③存在。

解法二：点差法。

由题意可知m≠0,设A(x1,y1)B(x2,y2),M(x0,y0)。

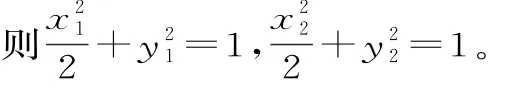
由题意知,点M(x0,y0)在椭圆内,故

解法三：利用根的分布求解。

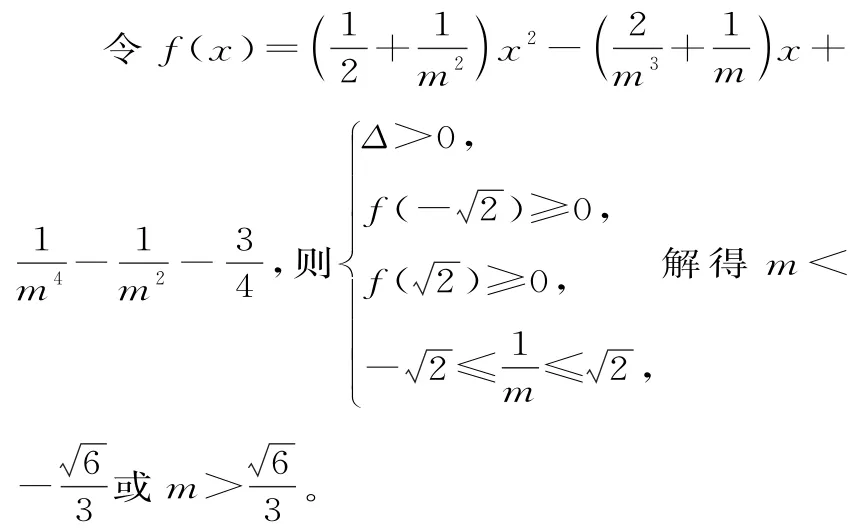
点评:“点差法”是解决中点弦问题时常见的方法。使用该方法有三个关键步骤:代入、做差、变形,其实质是建立曲线的弦的中点坐标与弦所在直线的斜率之间的关系,是“设而不求”思想的具体体现。若曲线C上存在不同的两点关于直线l对称,则等价于C上存在被直线l垂直平分的弦,即等价于弦的方程与C的方程组成的方程组在某确定的区间上有两个不同的解。因此可以利用一元二次方程根的分布来求解。

五、最值问题

例6已知A(-2,2)为定点,B是椭圆上的动点,F是右焦点,当取得最小值时,试求B点的坐标。

解析：由题意,过点B作l的垂线,垂足为N,过A作此准线的垂线,垂足为M。

复习建议：纵观近几年高考题,圆锥曲线考查内容较少,但是形式变化多端。考题难度上易、中、难三档题目都有,主要考查的知识点是圆锥曲线的概念、几何性质、直线与圆锥曲线的位置关系。同学们应提高自己的独立思考、逻辑推理、数学计算、数学应用和数形结合思想的应用等能力。