解析几何易错题归类剖析
■河南省项城市第一高级中学 尚晓琳
同学们在解题时,由于对知识点的理解不透彻,或考虑问题不全面等,可能会导致出现错误。本文分析了解析几何问题中的几个易错点,希望对同学们的学习能有所帮助。
一、倾斜角与斜率的关系中忽略斜率不存在的情况
例1(1)当a=3时,直线a x+(a-3)y-1=0的倾斜角是____。
(2)设直线l的方程为x+y·cosθ+3=0(θ∈R),则直线l的倾斜角∂的取值范围是____。
考查意图:本题考查直线的倾斜角、斜率及它们之间的关系,着重考查运算求解能力和数形结合的思想。
答案解析:(1)当a=3时,直线为3x-,所以倾斜角是90°。
(2)当cosθ=0时,x=-3,倾斜角是90°。
易错点:①易忽略cosθ=0的情况,此时斜率不存在;②不会用斜率与倾斜角的对应关系,如图1所示。
复习建议:①斜率与倾斜角的对应关系;②倾斜角的范围:当直线与x轴平行或者重合时,规定它的倾斜角是0°,直线的倾斜角范围是[0°,180°)。当直线斜率不存在时,倾斜角是90°。当时,斜率k≥0,斜率的值随着倾斜角的增大而增大;时,斜率k<0,斜率的值随着倾斜角的增大而减小。
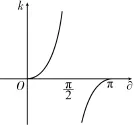
图1
二、忽略圆锥曲线方程的标准形式
例2若点M(5,3)到抛物线y=a x2的准线的距离是6,则抛物线的标准方程是( )。

考查意图:本题主要考查抛物线方程的四种标准形式。
答案解析:将y=a x2化为
综上,抛物线的标准方程为x2=1 2y或x2=-3 6y。故选D。
易错点:①误认为焦点在x轴上;②忽略a的正负在确定抛物线的开口方向上的不同。
知识点拨:①求抛物线的标准方程,常用待定系数法,因为只需确定未知量p;②抛物线方程的四种标准形式,求方程时,应先定位,再定量。
三、直线与圆的位置关系中易忽略斜率不存在的直线与圆相切
例3已知圆x2+y2=1和圆外一点P(1 , 2),过点P作圆的切线,则切线方程为____。
考查意图:直线与圆的位置关系。
答案解析:当直线的斜率不存在时,直线方程x=1,该直线是圆的切线。当直线的斜率存在时,设直线的方程是y-2=k(x-1),即k x-y-k+2=0。
综上,圆的切线方程为3x-4y+5=0或x=1。
易错点:易忽略斜率不存在的切线。
知识点拨:①过圆上一点,只有一条切线;②过圆外一点,有两条切线,如果求出的切线只有一条,那么需要结合图形把斜率不存在的那条切线补上。
四、忽视圆锥曲线的标准定义
例4平面内与定点A(-1,2)和定直线x+2y-3=0的距离相等的点M的轨迹是( )。
A.直线 B.抛物线
C.椭圆 D.圆
考查意图:本题主要考查抛物线的定义。
答案解析:易证点M在直线x+2y-3=0上,所以点M的轨迹为过原点且与已知直线垂直的直线,故正确答案为A。
易错点:忽视抛物线的严格定义。

