概率统计创新题型解析
■河南省项城市第一高级中学 胡德军
概率统计是实施新课标之后高考变化较大的一个模块,经过对近几年高考试题的观察分析,不难发现概率统计试题一般在新颖化、生活化的情境中,结合数学文化、社会热点,选取一些贴近生活的素材,考查学生提取信息、分析数据、解决问题的能力,以体现概率统计的应用价值。下面选取近年来各类数学考试中与概率统计相关的创新试题进行分析。
一、概率与数学文化结合
例1古希腊数学家阿基米德用穷竭法建立了这样的结论:“任何由直线和抛物线所包围的弓形,其面积都是其同底同高的三角形面积的三分之四。”如图1,已知直线x=2交抛物线y2=4x于A,B两点,点A,B在y轴上的射影分别为D,C。从长方形A B C D中任取一点,根据阿基米德这一理论,则该点位于阴影部分的概率为( )。
解析:在抛物线y2=4x中,取x=2,可得
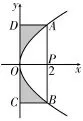
图1
点评:以数学文化为问题背景,考查几何概型是本题的一大亮点,整道题目打破以往常见的几何概型模式思维,借助于古代数学知识直接解题,显得新颖别致。
二、概率与社会热点交叉
例2PM 2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物。根据现行国家标准G B 3095-2012,PM 2.5日均值在35微克/立方米以下,空气质量为一级;在35微克/立方米~75微克/立方米之间,空气质量为二级;在75微克/立方米以上,空气质量为超标。从某自然保护区2017年全年每天的PM 2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如表1所示:
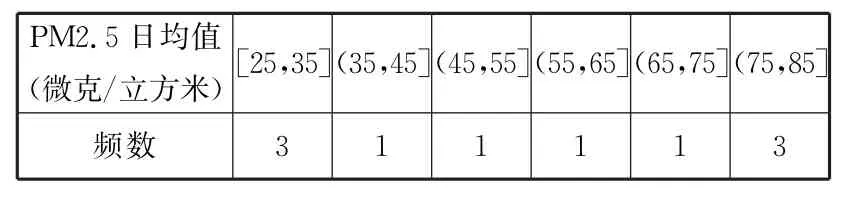
表1
(1)从这10天的PM 2.5日均值监测数据中,随机抽出3天,求恰有1天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据记ξ表示抽到PM 2.5监测数据超标的天数求ξ的分布列;
(3)以这10天的PM 2.5日均值来估计一年的空气质量情况,求一年(按365天计算)中平均有多少天的空气质量达到一级或二级(精确到整数)。
由测度比为面积比可得,点位于阴影部
解析:(1)记“从10天的P M 2.5日均值监测数据中,随机抽出3天,恰有1天空气质量达到一级”为事件A,则
(2)依据条件,ξ服从超几何分布,由题意可知ξ的可能取值为0,1,2,3,则P(ξ=0)
所以ξ的分布列为表2:
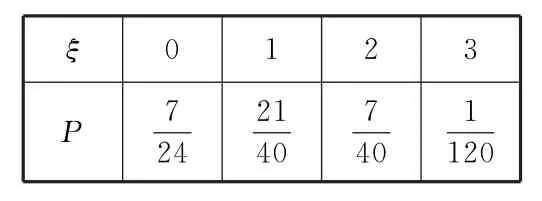
表2
(3)依题意可知,10天中每天空气质量达到一级或二级的天数有7天,即10天中空气质量达到一级或二级的概率为
点评:本题把随机变量的分布列与统计结合在一起进行考查,注重社会现实,体现时代精神,试题选择体现社会热点,主要考查了离散型随机变量的分布列、数学期望的求解,解题的关键是准确判断概率模型,求解相应的概率。
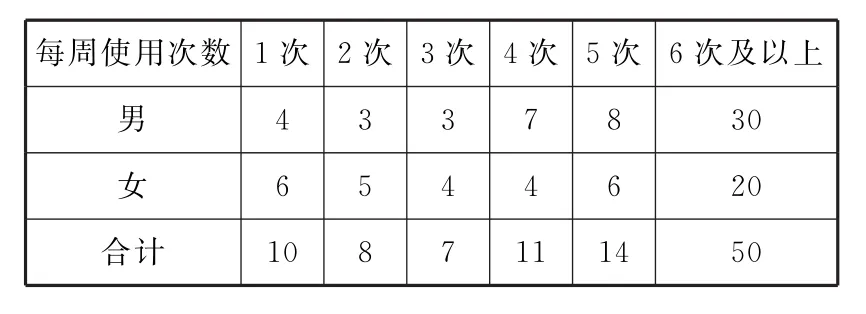
表3
(1)如果认为每周使用超过3次的用户为“喜欢骑行共享单车”,请完成2×2列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关。
(2)每周骑行共享单车6次及6次以上的用户称为“骑行达人”,视频率为概率,在我市所有“骑行达人”中,随机抽取4名用户。
①求抽取的4名用户中,既有男“骑行达人”,又有女“骑行达人”的概率;
②为了鼓励女性用户使用共享单车,对抽出的女“骑行达人”每人奖励500元,记奖励总金额为X,求X的分布列及数学期望。
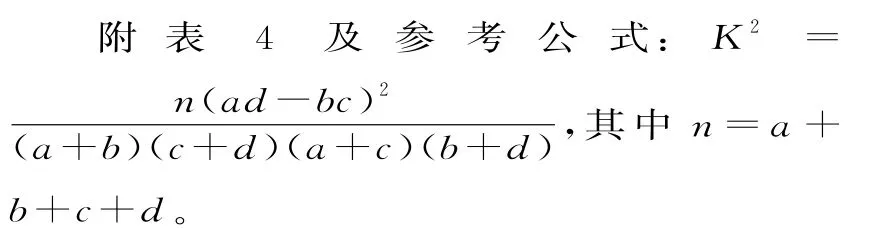

表4
解析:(1)由题中表格可得2×2列联表,如表5所示:
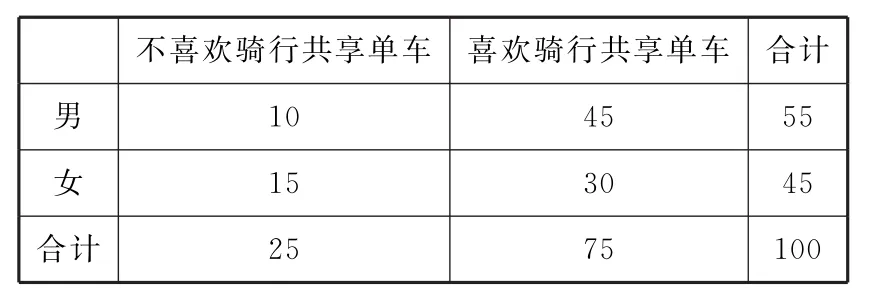
表5
(2)视频率为概率,在我市“骑行达人”中,随机抽取1名用户,该用户是男“骑行达人”的概率为,女“骑行达人”的概率为
①抽取的4名用户中,既有男“骑行达人”,又有女“骑行达人”的概率为:
为了降低贫镉液中钴含量,西北铅锌冶炼厂贫镉液采用合金锌粉与吐酒石除钴,控制温度80 ℃左右,反应1.5~2 h,间断除钴,每罐体积约40 m3,合金锌粉加入量按照贫镉液钴的30倍加入,除钴效果见表3。
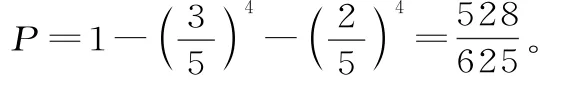
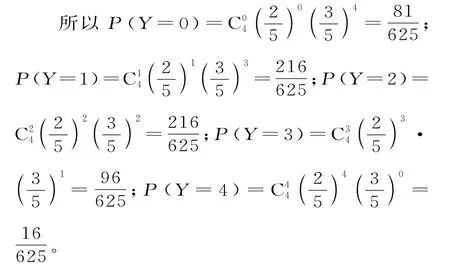
所以Y的分布列为表6:
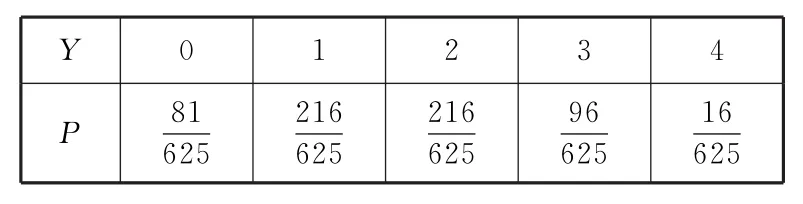
表6
所以X的分布列为表7:
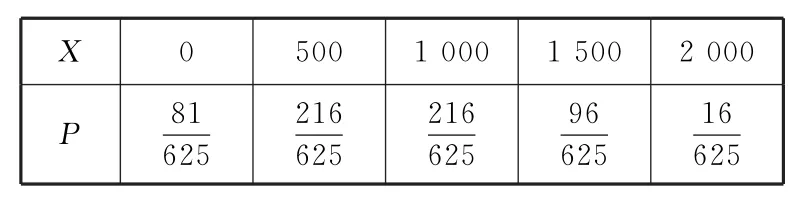
表7
点评:二项分布是一种常见的离散型随机变量的分布模型,利用二项分布可以快速地求出随机变量的分布列,从而简化了求解过程。而利用二项分布解决问题的关键是建立二项分布模型,也是看它是否满足n次独立重复试验,随机变量是否为这个n次独立重复试验中某事件发生的次数。
三、概率与生产生活牵手
例4菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜上仍有少量的残留农药,食用时需要用清水清洗干净,表8是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的统计表。
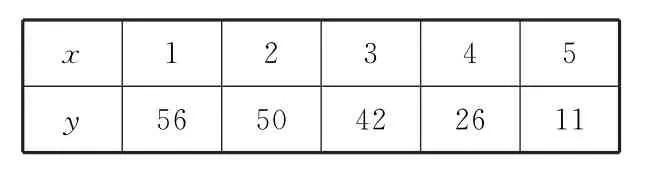
表8
(1)令w=x2,利用下列参考数据求出y关于w的回归方程^y=^b w+^a。(^a,^b精确到0.1)
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体是无害的,为了放心食用该蔬菜,请估计至少需用多少千克的清水清洗1千克蔬菜。(精确到0.1)
解析:(1)由题意可得
所以y关于w的回归方程为^y=-1.9w+57.9。

所以为了放心食用该蔬菜,估计需要用4.5千克的清水清洗1千克蔬菜。
点评:本题考查了线性回归方程的求法与应用问题。解决此类问题的关键是根据所给数据画出散点图,根据散点图判断两个变量之间是否具有相关关系,必要的时候还需要先进行变换,把非线性回归问题转化为线性回归问题进行分析,这种题型在前几年高考中有所涉及。

