基于渗流理论的城市交通网络瓶颈识别研究

吴若乾，周勇，陈振武

(深圳市城市交通规划设计研究中心有限公司，深圳市交通信息与交通工程重点实验室，广东深圳518021)

1 研究现状

交通流理论是一门运用物理学和数学定律描述交通特性的理论。交通流理论兴起于20世纪30年代，并于50年代得到迅速发展。到20世纪70年代，研究人员已分别从理论物理学、应用数学、经济学等多个学科领域对交通流进行研究，使其成为一门交叉性综合学科。20世纪80年代以后，交通流的研究进入平稳发展阶段。常用的交通流模型可分为三类：宏观模型、微观模型以及中观模型。

在宏观模型中，模型更关注的是交通流的宏观统计特性和所有车辆的总体平均行为，而并不在意车辆的个体行为，以及它们之间可能存在的相互作用。宏观模型包括流体动力学模型[1-2]和气体动理论模型[3]，分别采用流体动力学和气体力学的方法对车流量、密度和速度之间的关系和交通流宏观规律进行探究。在微观模型中，模型主要关注单个车辆的个体行为。每个车辆将被看作具有一定主观能动性的个体，能自主选择出行行为。微观模型主要包括车辆跟驰模型[4]和元胞自动机模型[5-6]，可以清晰地刻画车辆之间的相互作用，并分析车辆在运行过程中可能会出现的交通现象。在中观模型中，模型对于交通系统要素的细节描述程度比宏观模型高，但也并不需要像微观模型对每个车辆的交通行为进行细致刻画，交通行为的研究往往是以车辆队列为基础。

近年来，复杂网络的方法也为城市交通流的研究提供了新视角。从网络层面上对交通流进行分析，一方面要考虑网络的拓扑结构信息，另一方面还要考虑整体的交通流变化情况，因而网络层面上的交通流模型研究综合考虑了交通网络的结构和功能特性。文献[7]在2004年首先研究了包括交通网络在内的各种真实网络上流量的动力学特性。文献[8-10]针对不同网络拓扑结构和路由规则提出不同的交通流模型，研究了交通流从自由态到拥堵态的相变过程。

交通瓶颈是交通网络的薄弱环节。文献[11]指出当交通网络中某条路段的交通量超过路段自身固有的通行能力时，该条路段可被视为瓶颈路段，此时该路段上的车辆速度会有所降低，道路拥堵也会随之增加，道路服务水平下降。1969年，诺贝尔经济学奖得主威廉姆·维克瑞(William Vickrey)提出了著名的交通瓶颈模型，是最早用确定性排队理论，对存在瓶颈的路段研究出行者的出行时间模型[12]。文献[13]讨论了Vickrey模型在道路收费管理中的应用。1991年，文献[14]研究了高速公路上的瓶颈，探究了高速公路瓶颈处交通流的变化情况。1992年，文献[15]研究了拥堵情况下主干路的交通流特征。1993年，文献[16]将波动理论引入交通瓶颈研究中，并论证其实施可行性。以上对于交通瓶颈的研究多是从微观层面入手，即对局部区域内的交通瓶颈进行研究，而欠缺从整体交通网络的角度研究交通瓶颈[17]。

本文将借鉴统计物理学中的渗流理论对深圳市中心城区的交通网络进行动态交通流分析，探究从全局交通流到局部交通流的渗流相变过程，并且利用交通渗流临界过程的特性，从全网络连通性的角度对交通瓶颈进行全新的定义和识别。文章将分别从交通渗流的理论概述、交通渗流在深圳市中心城区的应用、交通网络瓶颈的识别和实际应用四部分内容进行研究。

2 交通渗流的理论概述

渗流理论主要描述当系统中某物理量占有量变化到某一定值时(渗流阈值)，系统宏观性质就会发生本质变化，导致系统长程联结性出现或者消失(相变)。在交通领域，文献[17]提出了交通渗流的概念，发现城市交通流的形成过程类似渗流过程，通过对实际交通数据进行分析，揭示了城市级别的全局交通流是由不同局部交通流所组成，并且会随时间不断地动态变化。

对于城市道路交通网络，本文首先对路网速度进行归一化处理。对于某条给定的道路，首先可以得到其在一天288个时刻的速度vij(t)(时间颗粒度为5 min)，将这些速度从小到大排列，设置95%的位置点所对应的速度值为该条道路的最大可通行速度vij-max，并以该值作为参考值，计算该条道路在全天所有时刻下的相对速度

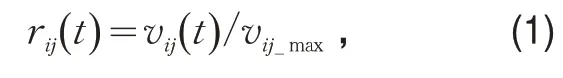
式中：rij(t)为起点i至终点j的道路上在时刻t的相对速度；vij(t)为起点i至终点j的道路上在时刻t的速度/(km·h-1)。按式(1)可对所有道路进行相同的速度预处理。

接着，本文将在渗流分析过程中引入速度阈值q的概念。对于给定的速度阈值q，当某条道路的相对速度rij()t大于等于阈值q时，认为该条道路处于畅通状态(sij=1)，而当某条道路的相对速度rij(t)小于阈值q时，认为该条道路处于拥堵状态(sij=0)，即

式中：sij(t)为起点i至终点j的道路在时刻t的交通状态。

因此，对于某个给定时刻下的交通网络，根据不同的速度阈值q，可以构建不同的动态交通流网络。在速度阈值q给定的情况下，通过将交通网络中所有道路的相对速度rij(t)与阈值q进行比较，可得到各条道路当前的交通状态，此时，网络中处于畅通状态(sij=1)的道路可以组成不同尺寸规模的功能连通子团。这些功能连通子团是由Tarjan算法计算得到的强连通集团，强连通集团内的任意两个节点均能通过合适的路径实现互通互达。其中，尺寸规模最大的功能连通子团G，可以被用来说明在给定速度阈值q水平下交通网络的整体连通程度。

图1 深圳市中心城区示意Fig.1 Layout of Shenzhen central area

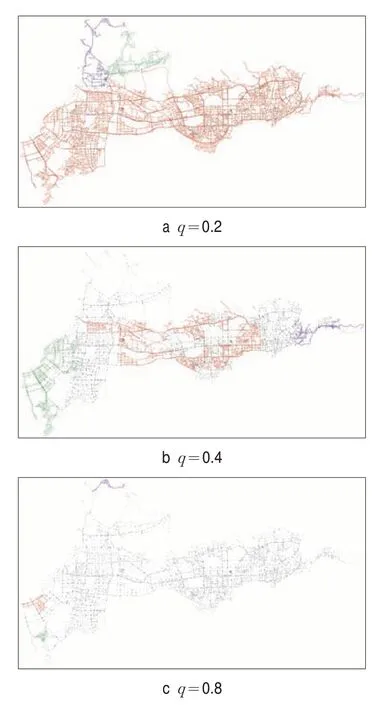
图2 不同速度阈值q水平下交通网络连通子团的空间分布Fig.2 Spatial distribution of connected components in traffic network under different speed threshold q

3 交通渗流在深圳市中心城区的应用

深圳市中心城区包括福田区、罗湖区和南山区(见图1)。文中所采用的交通网络数据包括深圳市中心城区的网络拓扑结构数据和对应的路网速度数据。其中，深圳市中心城区的交通网络包含了18 835个节点和34 356条有向连边。各个节点代表着特定的空间地理位置，具有详细的经纬度信息，各条有向连边则具有起讫点、长度和方向等信息。同时，本文采集了深圳市2018年5月约2.6亿条的速度数据。速度数据的采集是基于浮动车的实时速度数据，通过安装了GPS定位系统和无线通信设备的浮动车(如出租汽车)，可以得到浮动车的实时地理位置、速度以及方向信息，并将处于相同时刻相同道路上浮动车的速度数据进行平均处理从而得到该条道路在该时刻下的速度信息。速度数据所取用的时间间隔为5 min，因此全天能够被划分为288个时段，通过将速度数据中的道路信息与网络拓扑结构数据进行匹配，将速度信息映射到每条实际道路上，并进行相应的速度补偿处理，最终构建出动态交通流网络。

选取深圳市中心城区在2018年5月14日9:00的交通网络，以此为例说明交通渗流过程。图2描述了在不同速度阈值q水平下，交通网络中不同尺寸规模的功能连通子团的空间分布情况，其中橘色子团代表最大连通子团，绿色子团代表第二大(次大)连通子团，紫色子团代表第三大连通子团。当q值较小(q=0.2)时，网络中绝大部分的道路均处于畅通状态，因而形成的最大连通子团也基本能够覆盖全网络，而当q值较大(q=0.8)时，网络中大部分道路会处于拥堵状态，仅存在一些零星分布的连通子团。由此可知，当速度阈值q从0到1调节变化时，网络中被标记为拥堵的道路会逐渐增多，最大畅通连通子团的尺寸规模会逐渐减小，并最终崩溃消失(见图3)。在这个过程可以观察到网络中的全局交通流崩溃为局部交通流的动态组织过程，类似于理论物理中的渗流相变过程[18]，因而这一相变过程也被称为交通渗流。

图3描述了交通网络中的最大连通子团G的尺寸规模和次大连通子团SG的尺寸规模随q值的变化情况。当次大连通子团SG的尺寸规模达到最大值时，交通网络中原有的与系统规模相当的最大全局连通功能子团G将会崩溃为多个局部功能连通子团。根据渗流理论，此时网络中所对应的速度阈值q被定义为交通渗流临界阈值qc。

车辆能以低于渗流临界阈值qc的相对速度在交通网络中的绝大部分区域内自由行驶，而当车辆的相对速度大于临界阈值qc时，车辆则会受困于交通网络中的局部区域，而不能在全网络内自由行驶。因此，交通渗流临界阈值qc可以反映城市交通的运行组织效率，qc值越大意味着车辆在全局网络中畅通行驶的最大相对速度值越大，城市交通的运行组织效率越高。

按照上述方法对深圳市中心城区2018年5月的交通数据进行交通渗流分析，并对工作日和周末的结果进行平均，从而得到交通渗流临界阈值qc随时间t的变化情况(见图4)。工作日，交通渗流临界阈值qc的变化曲线存在两个明显的波谷，分别对应于早晚高峰。由于早晚高峰出行需求的急剧增加，网络中的部分路段会产生明显的拥堵，交通网络的整体连通情况也受到影响，早晚高峰的qc值要明显小于非高峰时段的qc值，城市交通的运行组织效率更低。而在周末，交通渗流临界阈值qc的变化曲线虽然也存在波动，但却没有工作日明显，而且上午波谷的出现时间要明显晚于工作日早高峰波谷出现的时间，这说明居民在周末会更倾向于推迟自己的出行时间。该结果也比较符合人们的生活实际。

因此，利用交通渗流临界阈值qc能够准确有效地衡量城市交通的整体运行情况，并能从交通网络结构和功能相结合的角度来说明城市交通整体运行状况，适用于城市交通运行指数评估等实际工作。

4 交通网络瓶颈识别

根据渗流理论，整个网络处于渗流临界处时会存在一个结构相对稀疏的主干网络，这个主干网络能以最少的节点维持整体网络的功能完整性。在这个主干网络中会存在一条或多条关键的“红边”，它们在连接不同的局域功能子团上起着不可替代的作用。在交通渗流研究中，交通网络瓶颈正是扮演着渗流理论中“红边”的角色，它对于维持全局网络交通流的正常运行起到关键作用。在交通渗流相变的过程中，必然会存在一条或多条关键路段，当这些路段的交通状态从畅通状态(sij=1)变为拥堵状态(sij=0)时，全局连通性受到影响，全局交通流将会崩溃为局部交通流。这些关键路段正是需要识别的交通网络瓶颈。

图5描述 了2018年5月14日17:00处 于交通渗流临界阈值qc前后的网络连通子团的分布情况。同上文相同，橘色子团代表最大连通子团；绿色子团代表第二大(次大)连通子团；黑色子团代表其他连通子团或是处于拥堵状态的路段。图5a描述了当速度阈值q略小于qc时，整个交通网络处于一个相对畅通的全局连通状态。而当速度阈值q略微增加时，某些道路的交通状态会从原来的畅通状态(sij=1)转变为拥堵状态(sij=0)，从而使得网络连通子团的分布情况发生变化，整个网络的畅通连通性也会受到影响。如图5b所示，原来的全局连通子团会因此而分裂形成多个局部连通子团。在渗流临界过程中，交通状态sij发生变化的道路则有可能是网络瓶颈道路。但并不是所有交通状态发生变化的道路都是瓶颈道路，接下来会对网络瓶颈进行进一步的识别。

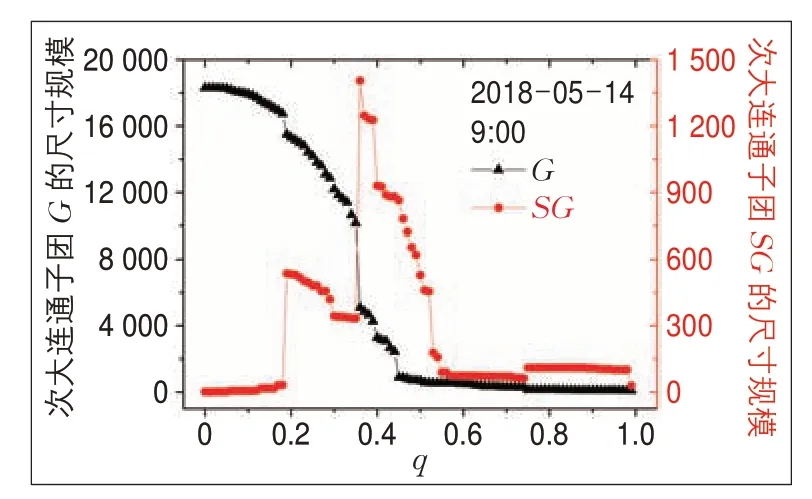
图3 交通渗流过程Fig.3 Process of traffic percolation

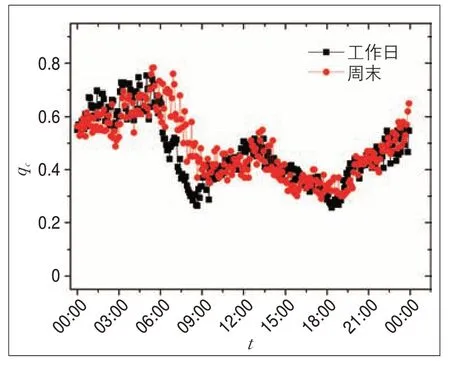
图4 交通渗流临界阈值qc随时间t的变化情况Fig.4 Changes of traffic percolation threshold qc with time t

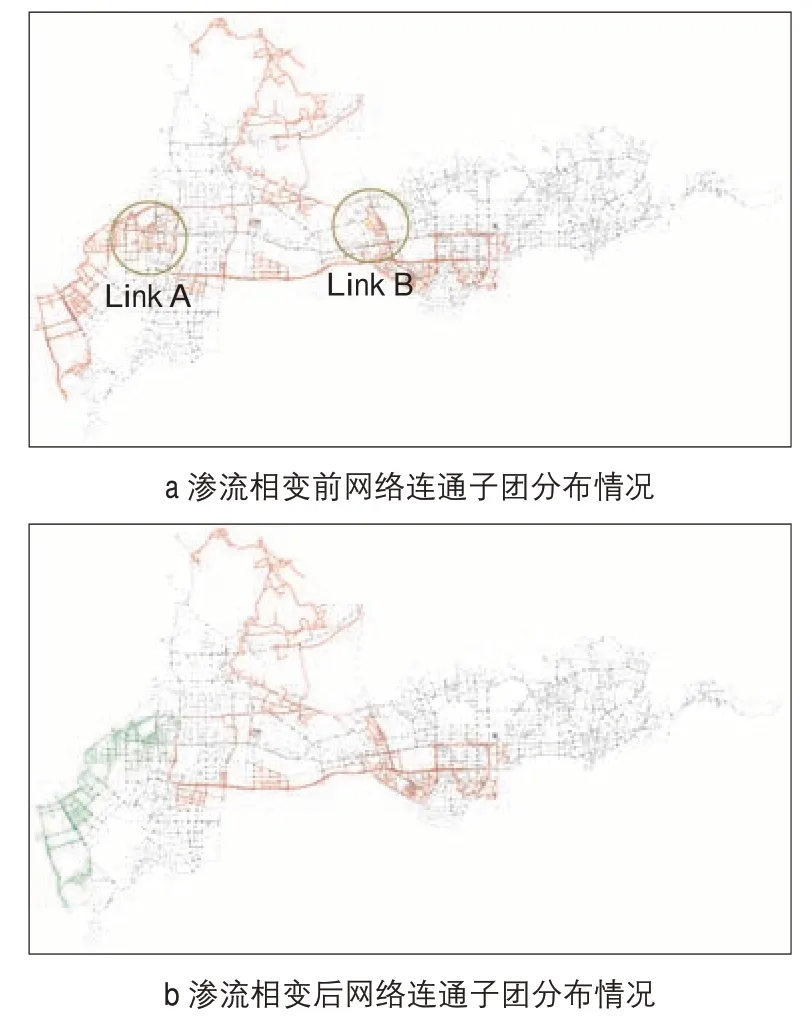
图5 渗流相变前后交通网络连通子团的分布情况Fig.5 Distribution of connected components in traffic network before and after the transition of traffic percolation

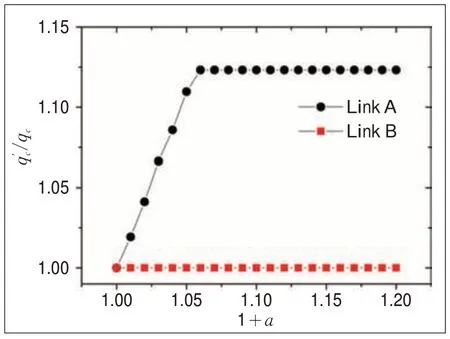
图6 基于交通渗流的网络瓶颈识别Fig.6 Identification of network bottlenecks based on traffic percolation

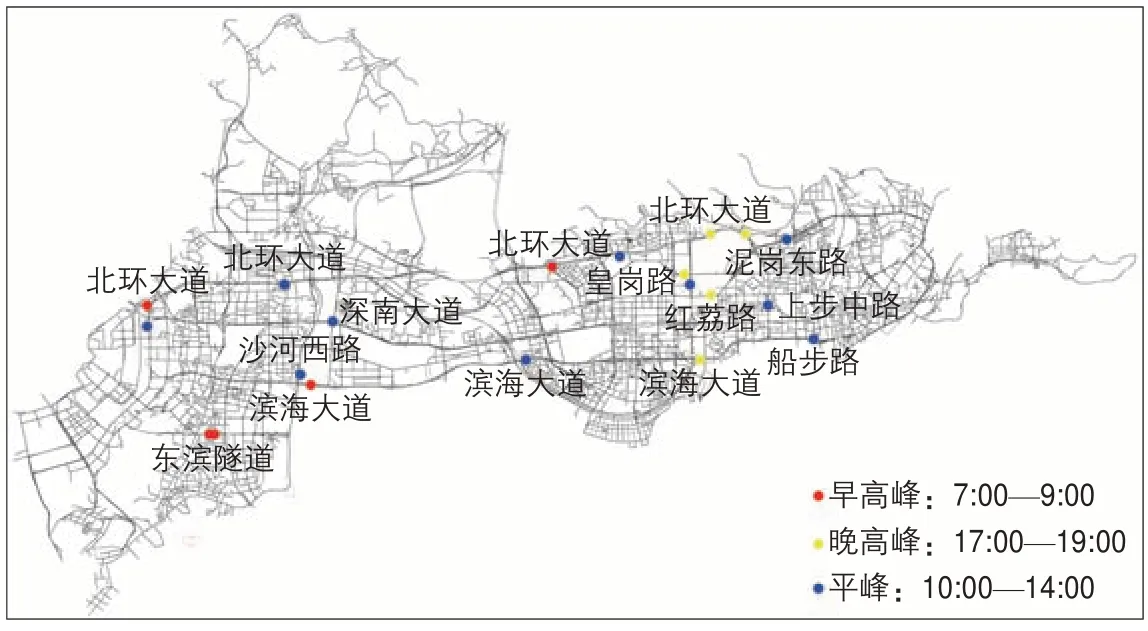
图7 交通网络瓶颈的空间分布情况Fig.7 Spatial distribution of traffic network bottlenecks

以图5a为例，渗流临界过程中会有黄色圆圈中的两条道路A和B的交通状态发生变化，它们均有可能是交通网络瓶颈。通过对两条道路进行“真假”判定，分别单独对两条道路上的相对速度rij进行不同程度α的提升，从而观察速度值调整后的交通渗流临界阈值的变化情况，即(见图6)。当对道路A的速度值进行调整时，交通渗流临界阈值明显发生变化；而对道路B的速度值进行调整时，交通渗流临界阈值则基本没有变化。因而，道路A才是对全局交通连通状态产生关键影响的道路，它的“失效”(畅通到拥堵)使得整个交通网络由全局连通状态转变为局部连通状态，这正是本文要寻找的交通网络瓶颈。

5 交通网络瓶颈在深圳市中心城区的应用

应用上述识别方法对2018年5月深圳市中心城区进行探究，分析早高峰(7:00—9:00)、晚高峰(17:00—19:00)和平峰(10:00—14:00)时段出现频次排名靠前的交通网络瓶颈的分布情况。通过交通网络瓶颈识别方法可以找到每个时段对全局连通性具有重要影响的瓶颈路段，通过对交通瓶颈出现频次进行统计，可以得到三个时段内出现频次较高的网络瓶颈路段。图7分别描述了早晚高峰排名前5以及平峰排名前10的网络瓶颈路段。

早高峰时段，交通网络瓶颈主要分布在通往深圳市中心城区西南部的前海和深圳湾的周边路段，其中包括滨海大道、东滨隧道及北环大道等路段。该区域聚集了大量企业，在早高峰时段有大量车流和人流涌入，易形成局部拥堵；该区域对外可替换路径较少，当这些关键瓶颈路段产生拥堵时，会很容易造成该区域从全局连通子团中分离。

晚高峰时段，交通网络瓶颈主要分布在福田区和罗湖区的一些分隔路段，其中包括北环大道东段，皇岗路、红荔路以及滨海大道东段等重要路段。大量车流经由福田区向罗湖区及外围行政区域移动，会在福田区造成拥堵，并且在福田区和罗湖区形成不同速度水平的连通子团，网络瓶颈也会在这些具有不同速度水平的连通子团之间的连接路段产生。

平峰时段，具有出现高频次的交通网络瓶颈的空间分布遍布全网络，具有一定的随机性。

通过对交通网络瓶颈在实际路网中的研究，得到对维持网络全局连通性具有关键作用的瓶颈路段，同时发现交通网络瓶颈在不同时段存在不同的分布规律。

6 结语

针对城市路网实际数据分析中发现的交通渗流现象以及交通网络中广泛存在的交通瓶颈问题，本文对深圳市中心城区的实际道路网络进行交通渗流分析，并在交通渗流过程中找到对维持全局交通流的完整性具有关键作用的交通网络瓶颈。在对深圳市实际路网的应用过程中，本文还发现交通渗流临界阈值qc能够作为衡量城市交通整体运行效率的有效指标。此外，交通网络瓶颈在不同时段存在不同的分布规律，这可从全局连通性的角度为优化交通瓶颈路段以及治理全局交通拥堵提供一些有益的建议。