一种新的选择集成算法

王道庆，孙浩军

（汕头大学工学院计算机系，广东 汕头 515063）

0 引 言

集成学习（ensemble learning）通过训练数据集来训练若干个有差异的个体学习器（base learning machine），并使用某种规则将这些个体学习器的学习结果进行整合.相对于单个学习器，集成学习在多数情况下可以显著提升学习系统的泛化性能.因此，人们在很多实际应用领域直接或间接地使用了集成学习算法.

集成学习可以利用多个学习器来获得比单一学习器更好的效果（泛化性能），因此一种较为直观的思路是通过大量的基学习器来获得更好的集成效果.目前，多数的集成学习算法是采取这种思路，其中最有代表性的是Boosting和Bagging算法.随着参与集成的学习器数量增多，集成学习的过程中不可避免地存在以下问题：集成的速度因为大量的基学习器产生和集合过程变得缓慢；集成的规模过大会占用较大的存储空间并耗费预测过程的时间.因此，人们开始考虑：使用较少量的基学习器是否可以达到更好的性能？2002年，周志华等[1]人提出了“选择性集成”的概念，对上述问题得出肯定的结论.相关的理论分析和实验研究表明，从已有的基学习器中将作用不大和性能不好的个体删除，只选出部分个体学习器用于构建集成确实可以得到更好的预测效果.

1 选择集成方法

选择集成算法的思想大体上都是在个体学习器生成和学习器集合这两个阶段之外再增加一个选择学习器或者剔除学习器的阶段.根据算法所采用的选择策略的不同，选择集成方法主要有以下几类：迭代优化法，聚类分簇法，排序法，其他类型.

迭代优化法中，周志华等[1]提出了基于实值编码遗传算法的选择性集成学习算法GASEN（Genetic Algorithm based Selective ENsemble），主要思想是用遗传算法来优化每个基分类器被赋予的权重，最终权重低于一定阈值的基学习器被剔除.受限于迭代优化方法的特性，GASEN等基于遗传算法的选择集成的收敛速度均较慢.爬山法应用于选择性集成的策略可以看做一个逐步求优的搜索过程，每次的搜索都建立在上一步的基础上，这种贪心策略可以使搜索空间较快地减小，速度得到提高.爬山法根据搜索的方向可以分为前向选择（Forward Selection）和后向消除（Backward Elimination）两种[2].爬山法的思想简单，但随着问题规模的扩大，在算法运行的初期的搜索空间仍较大，计算耗费仍不能控制在理想的范围内.

聚类分簇法一般首先采用某种聚类算法将相似的基分类器分在不同的簇，然后再在每个簇中选择一定数量的基分类器，最后进行集成.此类方法的思路是利用聚类操作来保证基分类器的多样性，辅以簇内选择操作来去除“无益”分类器.文献[3]从验证集分类结果构造的矩阵中得到不同基分类器间的欧氏距离，应用K-means聚类算法将基分类器进行分组，并根据基分类器子集的准确性和多样性进行选择.文献[4]定义了新的基分类器间的距离，然后采用层次凝聚的聚类算法来寻找相似预测结果的分类器簇，在算法的每一步后选择每个簇中到其他簇的平均距离最大的基分类器，采用简单投票法进行集成.再在形成的各种分类器子集中选取对验证集预测效果最佳的子集.此类方法根据选用的聚类策略的不同，计算时间耗费也不同，但总体上看也不是一种简单快速的方法.

排序法是采用某种特定的评估函数对所有基分类器进行排序，然后按照次序选择一定比例的基分类器.排序法最大优势在于选择速度快.目前排序法已经有很多算法取得不错的效果，其中方向排序[5]和边界距离最小化[6]这两种算法是比较有代表性且性能较好的.排序法的关键在于排序标准的确立.早期的算法大多依据预测性能等进行排序，但实验结果表明：个体基分类器预测性能好并不能保证集成分类器也有好的性能，所以还需结合分析分类器之间的相关性，使得分类器间具有互补性.排序法的另一个关键在于确立怎样的保留比例.一种是根据实验统计直接确定一个保留比例，一种是设定基于精度等度量的阈值，达到阈值的被保留.

总结各类选择集成方法的特点，本文在排序法的基础上采取“贪心策略”设计了一种快速剪枝选择集成算法（Fast Pruning Selective Ensemble，FPSE）.

2 FPSE算法

2.1 算法思路

由上节介绍可知，基于排序法的选择集成算法计算速度快，策略简单，但寻求一个合适的排序准则是关键.本文将提出的FPSE就是属于此类算法，但在排序策略上进行了一定的改进以求达到更好的效果.

在大多数的算法中，为了选择出最理想的分类器子集，会在训练数据集中单独分出一小部分数据集，可以用分类器在此数据集上的分类结果来评价其准确性，也可以根据各分类器的分类结果来计算分类器差异度，或者使用其他的评估指标计算依据.这种单独拿出部分训练数据的做法究竟是否会导致过拟合尚存在争议，但有一点可以肯定，因为用于训练的数据量减少，必然会影响基分类器的训练效果.

可以考虑设计一种无需损失训练数据集的方法来对基分类器进行评估，这样做可以使训练数据更完整，基分类器预测精度在总体上得到提升，从而达到提升集成系统效果的目的.在FPSE算法中设计了一种策略，即使用“包外样例”和全体训练数据分别评估“准确性”和“差异度”的办法来取代单独设置数据集进行基分类器评估，并把这种策略与一般评估策略进行性能对比.

算法的主要流程概括为：（1）首先根据泛化性能对全体分类器进行排序；（2）直接删除少量的较差个体分类器；（3）根据（1）、（2）步的结果，逐次选择泛化性能最差的个体分类器，若将其删除可以使剩余分类器差异度提高，则删除，否则保留，这一步的目的是保留下来的分类器有较大的差异度.

因为采取排序策略，所以算法的主要优势是快速简单，除此之外，分类器泛化性能和分类器间差异度的计算方法则是另一个优势.一般比较常用的做法是：首先从全体数据集中划分出一个验证集Mval，用于计算各基分类器Ci的准确性R：

各基分类器间差异性指标也一般使用验证集Mval来计算.但是这样的做法可能存在两方面缺陷：一是导致部分训练数据的损失，尤其在训练数据不够多的情况下，容易导致训练的模型欠拟合；二是将优化目标设定为一部分数据集（即Mval），在部分算法中可能会导致生成模型的偏移，不能接近最佳模型.

新算法不再单独设立验证集Mval从而避免上面提出的缺陷.FPSE算法的分类器生成阶段是采用Bagging算法的Bootstrap思路，在每个个体分类器生成的时候只使用了约63.2%的数据样例，剩下的约36.8%的样例则用来计算该分类器的泛化能力.分类器的差异度则评估每个分类器对整个训练集的判别结果的差异.

泛化性能的计算使用预测准确率就可以近似代替，但个体分类器间差异度的计算方式目前有很多选择.已经有很多个体学习器间的差异性（多样性）度量方法，如KW方差[7]，K度量[8]，难度度量θ[9]，广义多样性GD[10]，PCDM度量[11]，熵度量E[12]等.本文算法选用改进的熵度量E[13]作为评估分类器间差异程度的指标.

文献[13]提出的这种熵度量，没有使用对数函数，更易处理且能快速运算.这种度量方式的主要思想是利用多个分类器的分类结果的熵值来表征分类器间的差异程度.计算公式为：

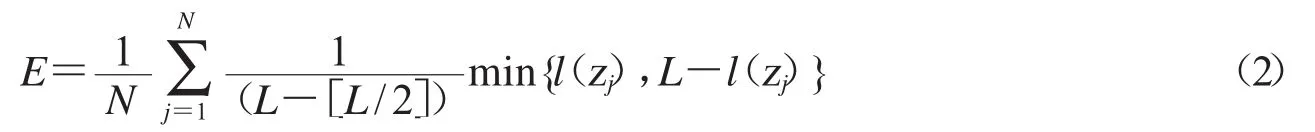
其中，N代表样例数，L代表基分类器数目，zj表示第j个样例，l（zj）表示对样例分类正确的分类器的数量.对于样例zj，如果所有的基分类器输出结果一致，即没有差异性，则此时熵度量值为0；如果一半（即个）的分类器分类正确，另一半错误，则熵度量值为1，此时集成系统的差异性最大.

不妨记上述熵度量为Ent，记经典熵度量[12]为Ecc，假设在分类器数量无穷多情况下，a为正确分类数量占比，两种度量方式结果为：

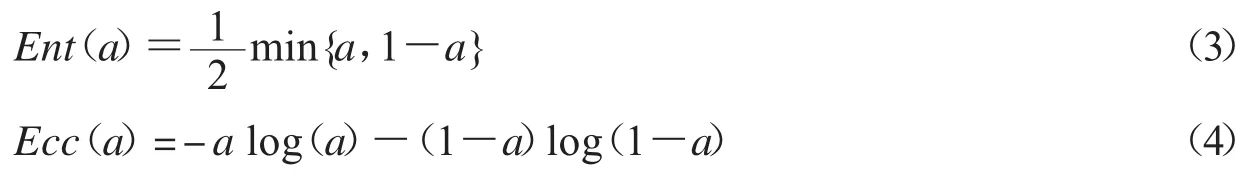
图1显示了两种熵值与a的关系，其中横坐标代表a值，纵坐标代表熵值.这两种度量在计算效果上基本相当，但显然运算速度上Ent要更快速.

图1 两种熵度量与分类正确占比a的关系

2.2 FPSE算法

上节说明了算法的一些关键问题，并阐述了算法设计的思路.下面是FPSE算法的完整表述.

算法描述：

输入：数据集D＝（{x1，y1），（x2，y2），…，（xm，ym）}；基学习算法L；初始基分类器数量T；初步删除比例k1，最终保留比例k2，差异度最小提升量ΔE；

输出：对每个新样例点x，集成系统的预测结果为

过程：

1.for t＝1，2，…，T do；

2.ht＝L（tD，Dbootstra）p；

3.end for；

4.计算每个分类器在包外样本上的准确率Acchi；

5.根据准确率排序分类器得集合{h1，h2，…，hT（}Acchi＜Acchi＋1）；

6.根据初步删除比例k1删除掉分类器集合前部分的分类器，剩余集合S{m1，m2，…，mi，…（}Accmi＜Accmi＋1），剩余数量Num；

7.while Numbers＞k2*Num；

8.计算当前分类器群差异度Enow；

9.计算去除第i个分类器后，分类器群体差异度Enext；

10.if Enext－Enow＞ΔE；

11.delete mifrom S；

12.i＋＋；

13.已经删除该基分类器，返回7；

14.无法继续删除过程或删除数量达到阈值，停止；

15.简单投票法集成剩余分类器.

3 实验结果与分析

3.1 实验设置

本文根据算法的类型、样本适应等因素，选取了UCI数据库中的12个数据集来测试FPSE算法的性能.为进行对比实验，使用开源算法包sklearn上提供的几个分类学习算法作为对照组，它们分别是：Cart决策树、支持向量机、AdaBoost算法、Bagging算法.其中AdaBoost算法、Bagging算法以及本文FPSE算法都将使用Cart决策树生成基分类器.为验证本文算法对差异度和泛化性能评价所做改进的有效性，在训练集中设置验证集作为优化目标并嵌入进本文算法中，不妨称之为FPSE-useVal.并加入对照组.

实验中，将数据全集随机分开，80%用作训练集，20%用作测试集.对每个数据集重复此过程50次.

使用分类结果的正确率作为评价指标，计算公式如下：

其中，N为样例数量（分类器预测的次数）；Ci在分类器预测正确时为1，错误时为0.本式代表分类器预测结果的总命中数占预测次数的比例.

本文使用了12个数据集作为算法的测试，数据集都来源于UCI.这12个数据集分别是：iris，wine，banlance-scale，ecoli，glass，breast-cancer-wisconsin，zoo，pima-indiansdiabetes，transfusion，contraceptive-method-choice，habermans-survival，ionosphere.数据集基本信息见表1.

3.2 实验结果与分析

实验结果见表2.在正确率指标值后方加入误差波动范围值供参考，该数值取的是50次实验结果的标准差.

表1 数据集基本信息表

表2 各算法在数据集上的正确率表（决策树作为基分类器）

图2和图3描述了DT-Tree、SVM、AdaBoost、Bagging、FPSE-u和FPSE等6个算法分别在12个数据集上的分类准确率.

图2 算法在数据集上的正确率直方图part1

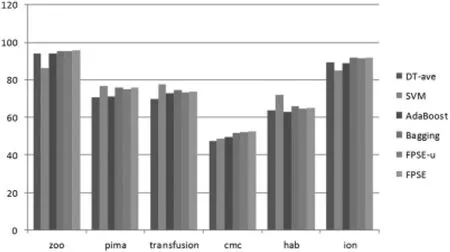
图3 算法在数据集上的正确率直方图part2

因为统一选用决策树作为基分类器，使得AdaBoost算法、Bagging算法和本文的FPSE算法的对比更客观.就正确率而言（见表2），有以下几点值得关注：

（1）FPSE算法明显比基分类算法（Cart决策树）的平均正确率高（最少1个百分点，最多8个百分点）；

（2）FPSE算法除了在pima-indians-diabetes、transfusion、habermans-survival三个数据集上表现略逊于Bagging算法，在其他的9个数据集上正确率都优于Bagging算法.在全部12个数据集上，FPSE算法与AdaBoost算法相比，正确率具有明显优势；

（3）可以看到，单独设置验证集的本文算法的变型FPSE-useVal算法的正确率表现在全体12个数据上都逊于本文FPSE算法.这也就是说明FPSE算法使用的分类器评估策略是有效的，比单独设置数据集来评估分类器性能的做法更能提升集成泛化性能；

（4）在 ecoli、glass、zoo、ionosphere、contraceptive-method-choice 数据集上，本文FPSE算法比SVM算法的正确率表现得更优秀；

（5）参考误差范围值，FPSE算法的正确率变化也较为稳定.

4 总结

本文主要提出了一种新的选择性集成学习算法.其主要的优势是能够较为显著地提升一个学习系统的泛化能力，在部分数据集上的表现大致与Bagging算法和AdaBoost算法相当甚至略优于它们.本文工作的一个特色在于，提出了一种计算分类器的预测准确性和群体差异性的方法，且无需单独设置部分数据集.使用此方法确实可以进一步提升集成系统的预测性能.

后续还可以继续展开的工作有：选取更多的数据集来验证FPSE算法的效能，并在实际应用领域使用FPSE算法来解决分类问题；对FPSE算法中个体分类器评估的做法进行概括与改进，并嵌入其他的一些选择集成算法，验证此做法是否具有普适性.