由微分算子L定义的单叶调和函数新子类

黄叶腾

（汕头大学数学系，广东 汕头 515063）

0 引言

在一个单连通区域Ω上，一个连续复值函数f＝u＋iv称为调和函数，如果它的实部和虚部都是实调和函数.在任意的单连通区域Ω内我们可以记：，其中h和g都是解析的.在区域Ω内，f是局部单叶和保向调和的当且仅当[1].在1984年，Clunie和Sheil-Small[1]引入了函数类SH与它的子类，并且还得到了一些系数估计.自从那以后便出现了很多关于单叶调和函数子类的文章，我们可以通过查找参考文献[2-4]来了解这类调和映射的最新研究进展.在文献[5]中，Jahangi证明了f是α星形单叶的，并且研究了单叶调和函数类，其中0≤α＜1.在文献[6]中，作者利用L算子把上述函数类进行了推广，他们引入了两个单叶函数类：，其中 0≤α＜1，0≤≤1.在文献[7]中，作者利用L算子定义了Goodman-Rønning-type单叶调和函数类G（Hα）.

受到上面文章的启发，利用线性微分算子L，我们定义了两个单叶调和函数类：GH（，α，ρ）与TG（H，α，ρ），并研究了它们的相关性质.另外，我们还获得关于这类调和映射的系数条件，偏差定理，极值点，以及他们在凸组合和卷积运算下的不变性.

1 准备知识

令SH表示所有定义在单位圆盘D上且单叶和保向的调和函数f＝h＋构成的集合，其中

定义1 我们定义线性微分算子L如下：

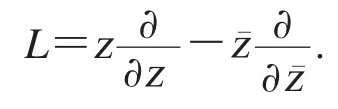
定义2 设GH（，α，ρ）表示所有满足下面条件的单叶调和函数f＝h＋构成的集合：

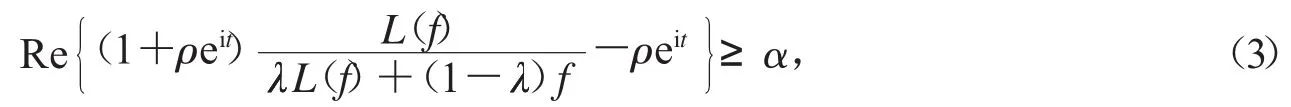
我们进一步定义GH（，α，ρ）的子类TGH（，α，ρ），其中 TGH（，α，ρ）中的函数 f具有如下形式：

2 主要结果及证明

2.1 系数估计

我们首先讨论的是调和映射f∈GH（，α，ρ）的一个充分条件.

其中

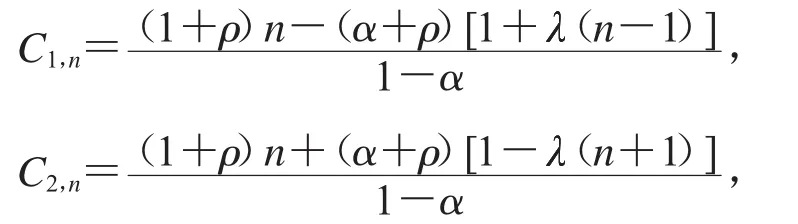
a1＝1，0≤α＜1，0≤≤1，ρ≥0，那么f是保向单叶的.若≤（1－α）/（1＋α），则f∈GH（，α，ρ）.

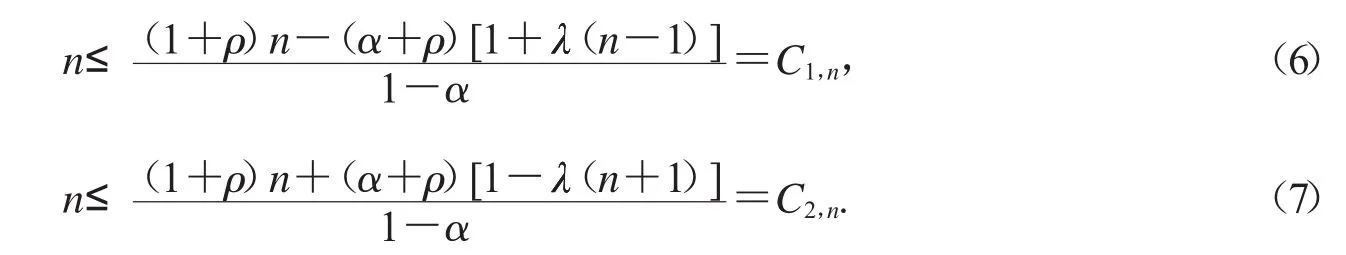
故由（5）－（7）知

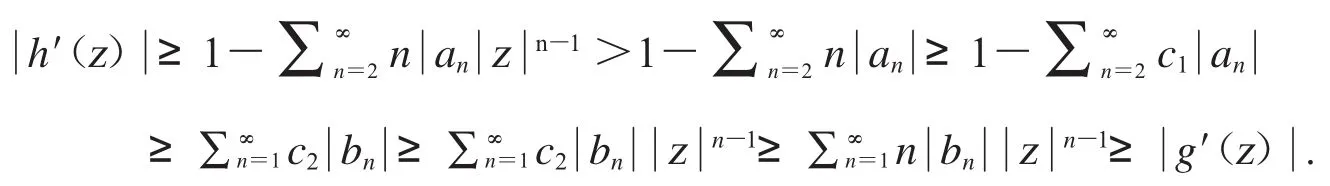
因此，f是保向的.

我们注意到，如果g（z）≡0，那么（fz）是解析单叶的，因为GH（，α，ρ）中的映射均为单叶的.如果，那么我们要证明f是单叶的，只需证明对任意的，有.

不失一般性，不妨设f不是恒等映射.设z1和z2是D中任意两个不同的点，故由（5）－（7）可知

因此，f在单位圆D内是单叶的.

其中

替换（8）中的 A（z）和 B（z），再由系数条件（5）和≤1－α/（1＋α）知，

和

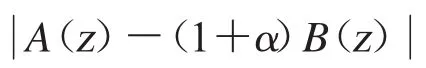
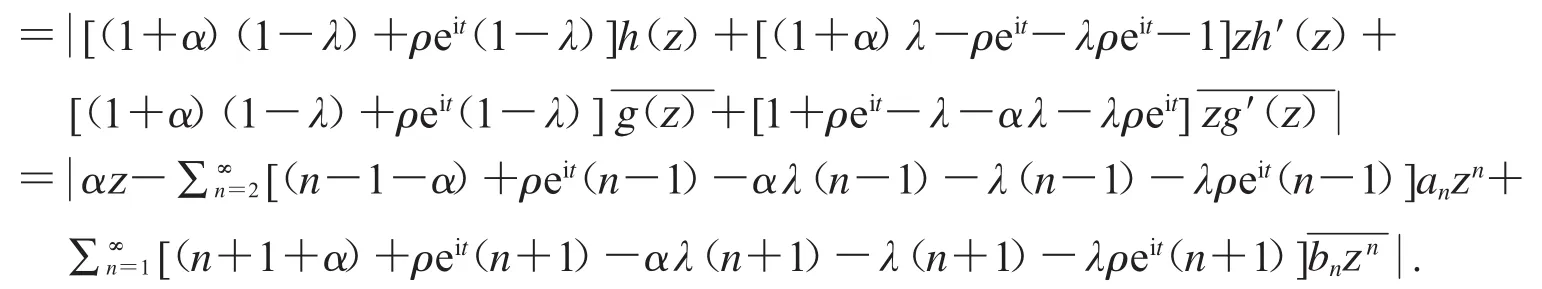
因此，

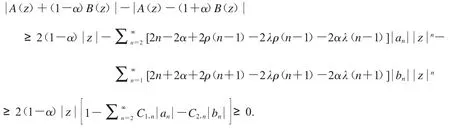
从而，f∈GH（，α，ρ），定理 1 得证.

注2 下面的调和函数f是定理1中系数条件（5）能取到等号的结果.

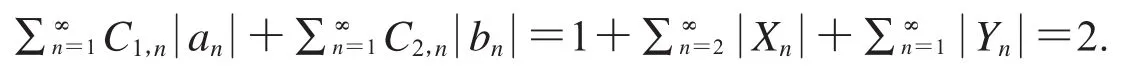
因此，函数f∈GH（，α，ρ）.

其中 a1＝1，0≤α＜1，0≤≤1，ρ≥0，≤1－α/（1＋α），且C1，n，C2，n为定理1中系数.

证明 因为TGH（，α，ρ）⊂GH（，α，ρ），我们只需要证明这个定理的必要部分即可.由（3）知，

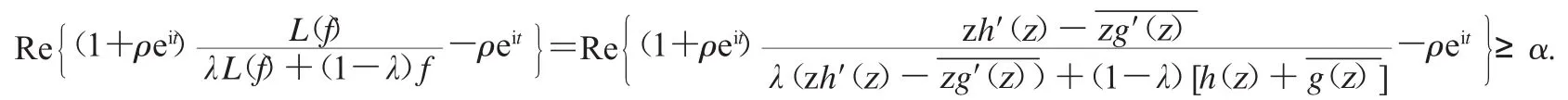
而上面条件又等价于

由于上面的条件必须对所有的z∈D都成立，为了计算方便，取z为正实数，即0＜z＝r＜1.我们可以得到

其中

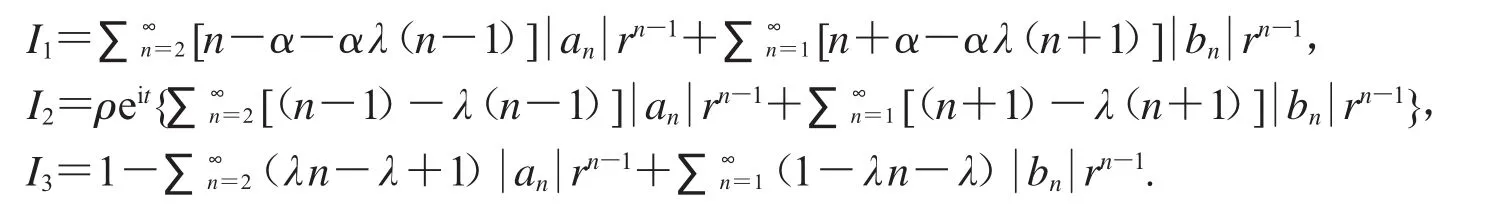
其中

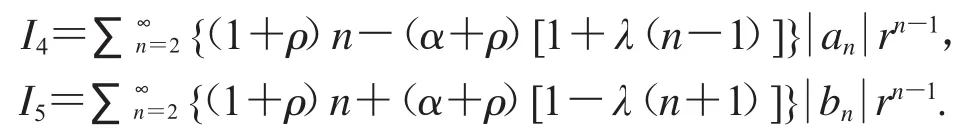
定义3[8]对于D上的单叶函数f，如果曲线（frei）t关于原点是星形的，那么称函数f是星形的，其中0＜r＜1，（f0）＝0.换句话说，如果，那么函数f是星形的.

下面引理是星形函数和L算子之间的一个等价关系.

引理1[8].

推论1 如果f∈TGH（，α，ρ），那么 f是星形的.

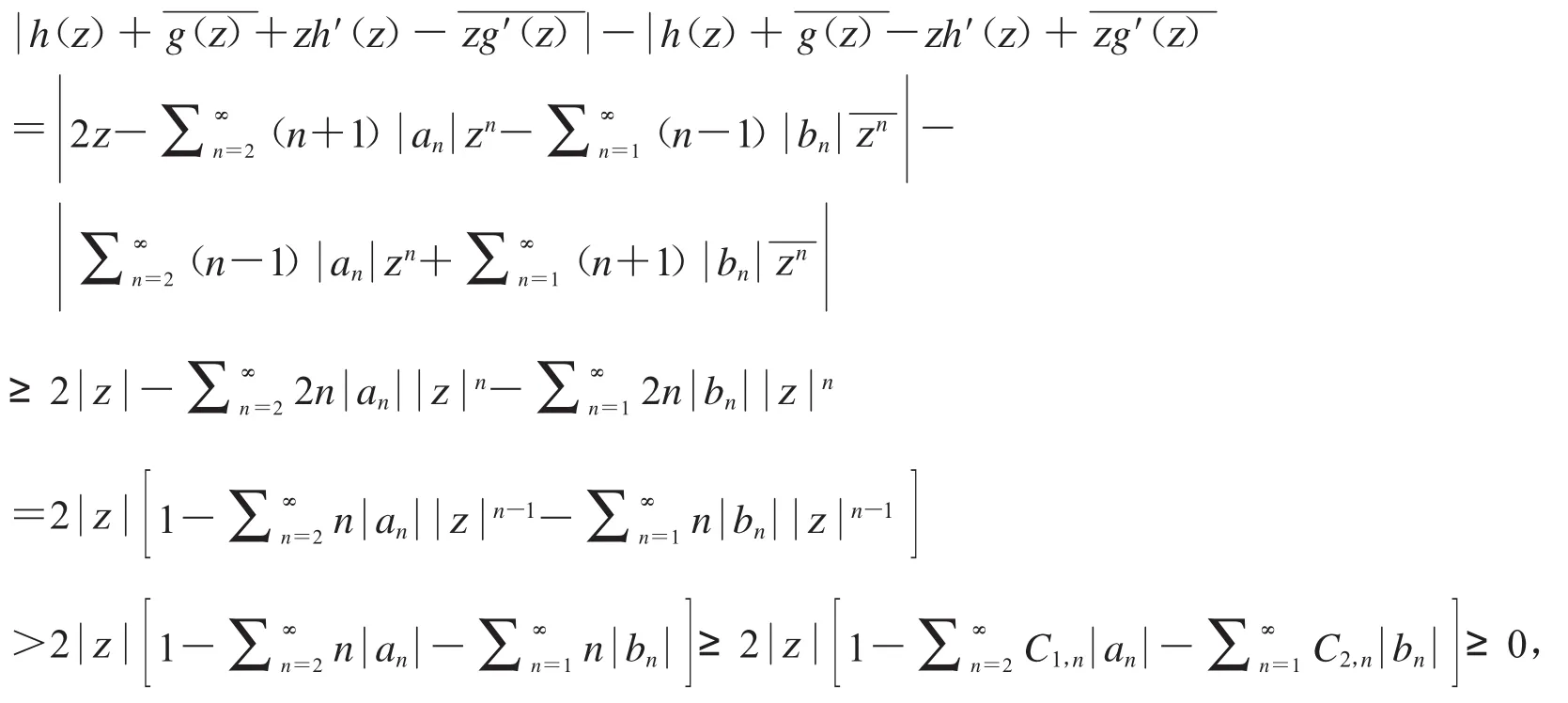
[由（9）知]

其中 C1，n，C2，n为定理1中系数.因此，推论1得证.

2.2 偏差定理

定理3 如果f∈TGH（，α，ρ），那么

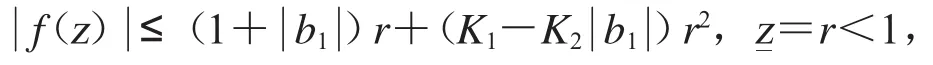
和

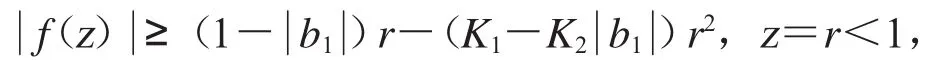
其中

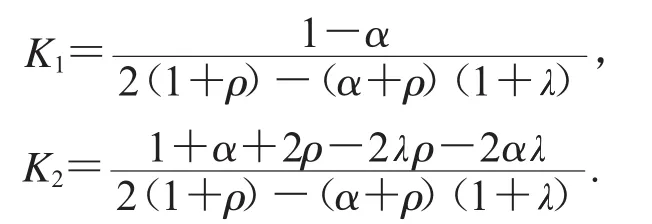
证明 设 f∈TGH（，α，ρ），则

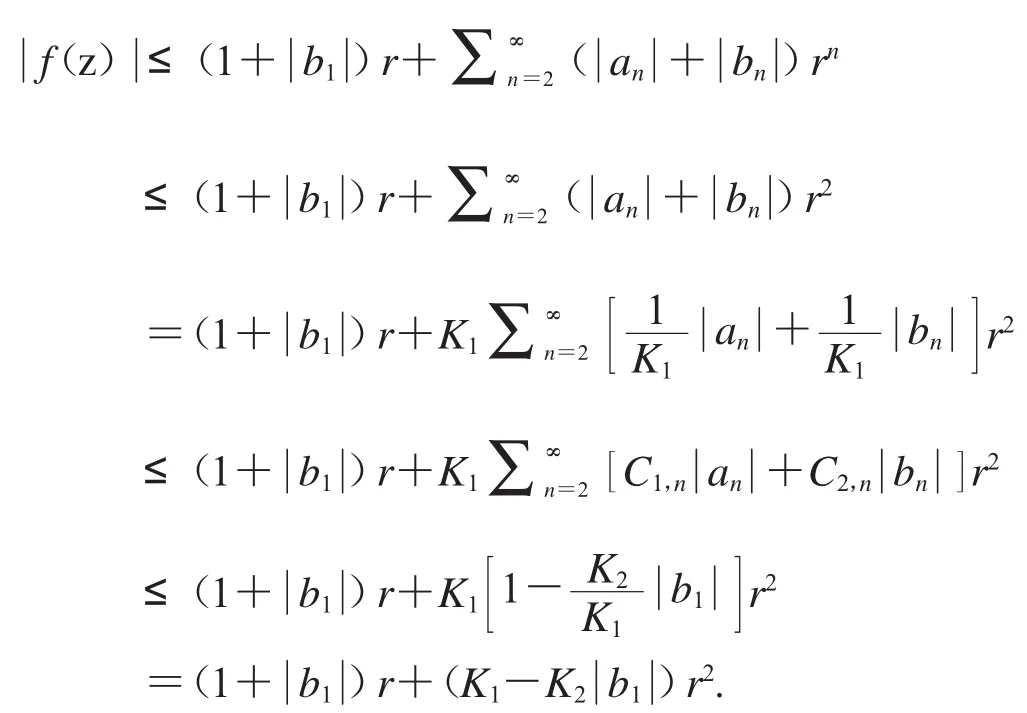
同理，可证

其中C1，n，C2，n为定理 1 中系数.因此，定理3得证.

显然，由定理3可得以下覆盖定理.

推论2 如果f∈TGH（，α，ρ），那么

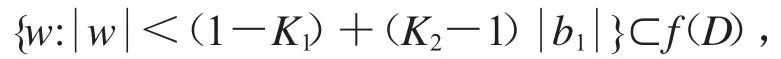
其中K1，K2定理3中的系数.

2.3 极值点，凸组合和卷积

定理4 f∈TGH（，α，ρ）当且仅当

这里

且 C1，n，C2，n为定理1中系数.特别地，TGH（，α，ρ）的极值点是以上定义的两类映射{hn}和{gn}.

证明 对于具有形式（11）的函数f，我们有

那么

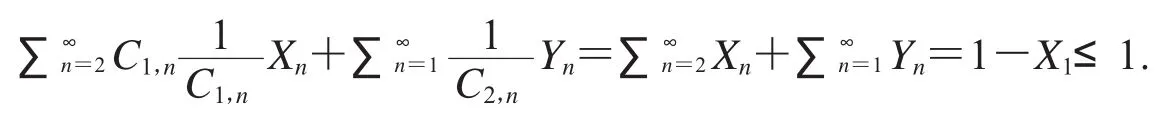
因此，f∈TGH（，α，ρ）.

反过来，如果f∈TGH（，α，ρ），我们设

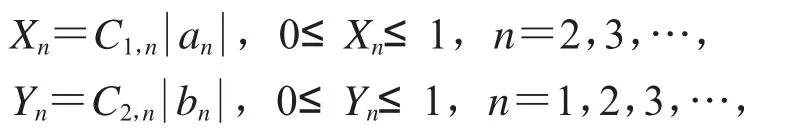
定理得证.

定理5 函数类TGH（，α，ρ）中的元素在凸组合运算下是不变的.

证明 对于i＝1，2，3，…，设fi∈TGH（，α，ρ），其中 fi被记为如下形式：

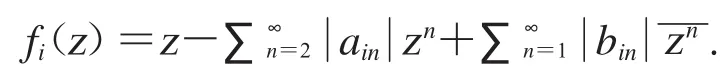
则由式（9）知

那么由式（12）可得，

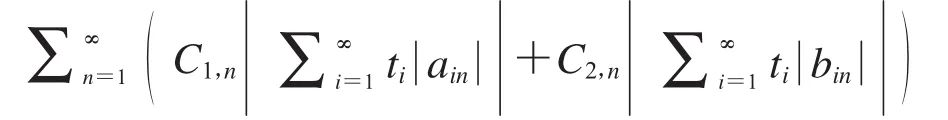
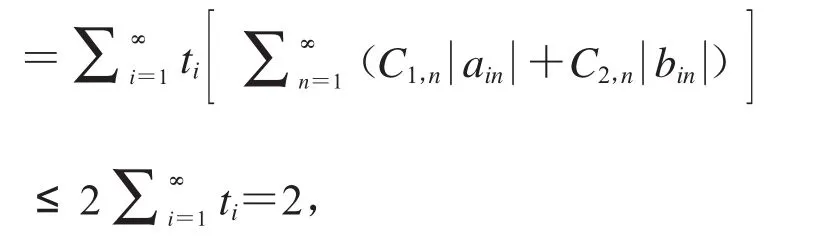
其中C1，n，C2，n为定理1中系数.从而，得证.

最后，我们根据调和函数卷积的定义来证明函数类TGH（，α，ρ）关于卷积的运算的封闭性.所得结果如定理6.

定理6 设f∈TGH（，α，ρ），F∈TGH（，β，ρ），0≤β≤α＜1，那么

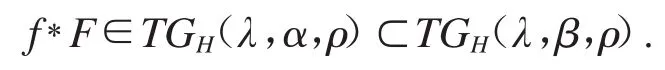
证明设

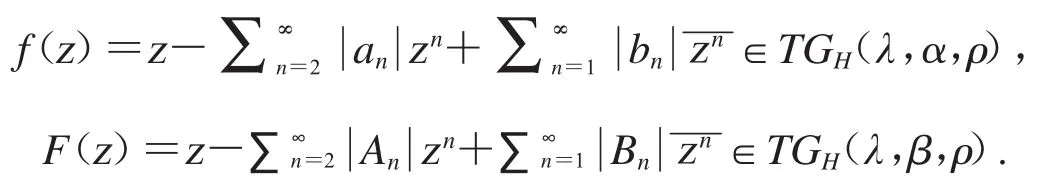
因为 F∈TGH（，β，ρ），故.

由定义4知，

所以

故f*F∈TGH（，α，ρ）.

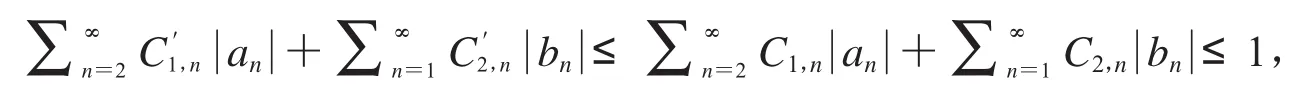
从而TGH（，α，ρ）⊂TGH（，β，ρ），其中

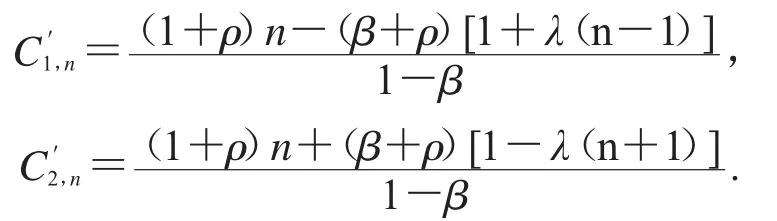
且 C1，n，C2，n为定理 1 中系数.因此，f*F∈TGH（，α，ρ）⊂TGH（，β，ρ）.