压缩感知理论及重建方法
刘 蕾,李建东,闫敬文*
(1.汕头大学医学院,广东 汕头 515063;2.汕头大学工学院电子系,广东 汕头 515063)
0 引言
随着各类医疗成像、高清遥感、视频监控等技术的飞速发展及应用,现代化成像和信息技术获取数据的能力得到不断地增强,大体积高维度的海量数据使得我们急需提高快速处理数据的能力.传统的数据获取模式要求信号的采集频率必须大于或等于信号带宽两倍,才能精确恢复原信号.按照传统信号采集模式,采集后的信号需先储存再压缩传输,这将导致大量的冗余数据被保留下来,增大采样硬件成本,且大量的采集数据在压缩中被抛弃,大大降低了采样效率和硬件的利用效率,极大限制了高效信号处理的要求.传统信号获取方式的缺陷促使学者们不断研究新的信号获取方法.2006年,论文“Compressed Sensing”的发表标志着CS理论框架正式被提出[1].Donoho等研究者指出,针对稀疏或可压缩信号,可以采用非线性采样,在采样的同时对数据进行压缩,提高传感器的采样效率,同时也避免大量冗余数据被保留而占用有限的储存资源[1-2].由于压缩感知理论运用非相关测量矩阵进行压缩采样,其采样频率可远低于奈奎斯特频率,再按照非线性优化的重构算法,把复杂的恢复计算部分交给数据还原的这一端来做,精确重构原始信号[1-3].图1给出了传统数据传输与CS数据传输的区别示意图.
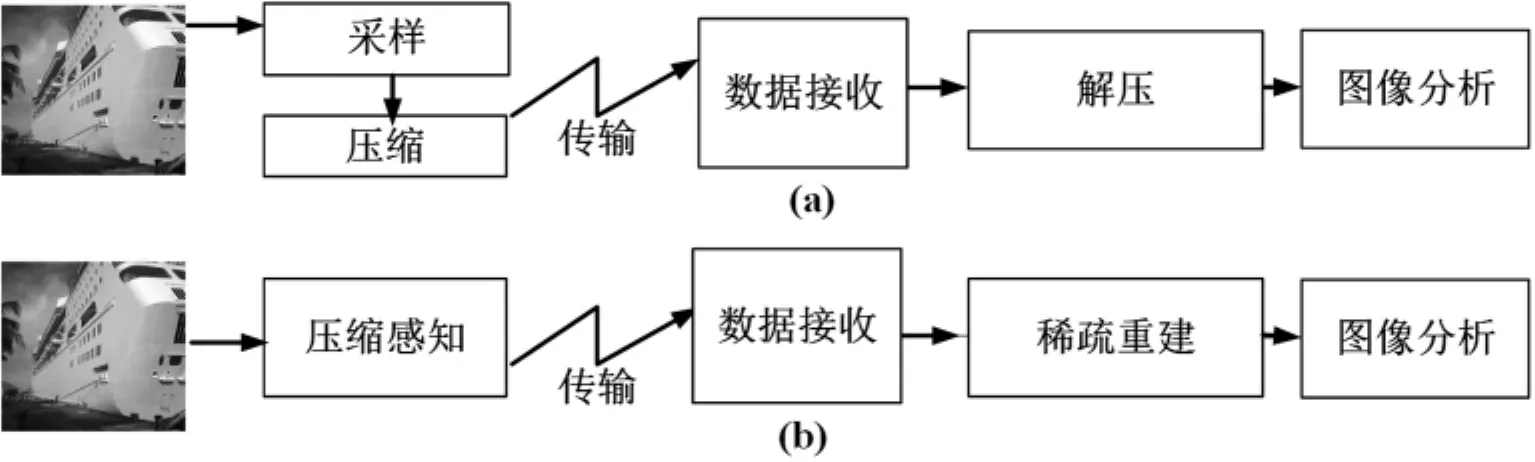
图1 传统数据传输和CS数据传输.
1 压缩感知的理论框架基础
基于压缩感知非相关矩阵获取的投影测量值的数据量远远小于传统采样方法所获的数据量,这不仅突破了采样定理对精确重构信号时采样频率的限制,而且提高了数据采集端的采样、储存及传输效率[2-3].尤其是针对搭载在飞机或卫星上的传感器采集系统而言,压缩感知理论减少了大量数据的存储空间,提高了的传输效率和传感器的利用效率.压缩感知理论指出,信号或图像精确重建必须满足以下三个条件[4]:
(1)稀疏性,即在某种变换域下信号或图像可被稀疏表示;
(2)测量矩阵满足限制等容性准则(Restricted Isometry Property,RIP)条件,即要满足与信号本身是互不相干的;
(3)通过非线性优化的重建模型精确重建.
1.1 压缩感知重建的基本知识
1.1.1 稀疏信号及信号的稀疏表示
稀疏信号是指信号中只有少数元素是非零的[2].根据压缩感知理论,图像的重建误差界是由稀疏逼近误差决定的[5].对于任一信号x∈Rn,令是满足压缩感知条件的解,ΨT表示正变换,则ΨTx表示信号x在变换域ΨT下的稀疏表示,我们仅保留s个最大系数即可得到x在变换域ΨT下稀疏逼近表示,用(ΨTx)s表示,则重建误差可由公式(1)给出:

其中C0,C1是很小的正数,ε表示噪声水平[6].公式(1)显示更加稀疏的表示可以降低重建误差,因此稀疏性对提高信号或图像重建质量起着关键作用.
鉴于我们通常获取的自然信号或图像都是非稀疏的,因此稀疏性的核心思想是寻找Parseval框架一组基或紧框架下的冗余字典(Ψ={Ψm}m),使得信号或图像在该组基或字典上的投影只存在少数几个大的分量,其他的分量都为零(稀疏的)或者接近零(可压缩的)[6].常见的稀疏表示方法有傅里叶变换[7]、离散余弦变换DCT、小波变换[7]以及多尺度几何分析、稀疏字典表示[8]等.典型的多尺度几何分析方法包括Meyer和Coifman提出的 Brushlet变换[9],Candès提出的紧框架 Ridgelet变换[10]和 Curvelet变换[11],Do 提出的紧框架Contourlet变换[12-13]和Labate提出的Shearlet变换[14-15],Lu和Do[16]提了紧框架Surfacelet变换等.尤其是针对高维数据,图像的边界面通常是曲面奇异的[16],多尺度几何分析能够更好地捕捉高维信号的曲面奇异性,比固定方向的变换有更好的稀疏表示的性质.
1.1.2 测量矩阵及不相干性
采样矩阵和稀疏变换基之间的不相干性是压缩感知理论成立的另一重要特点.不相关性是指压缩感知编码矩阵的列向量必须在相应的稀疏基上扩散[3].如果用A表示采样矩阵Φ和稀疏变换基Ψ的乘积,若A满足限制等容性准则(Restricted Isometry Property,RIP)条件才能保证信号成功重建[5].互相干性(mutual-coherence)提供任意两个列向量之间相似性的最大值[17],这是一种最坏的情况,因为两个相似的列向量会混淆所有基追踪算法(pursuit algorithm)[18].但是,互相干性没有真正反映稀疏表示行为和基追踪算法的性能.互相干性系数设为,对此,Elad提出使用平均相干性(t-averaged mutual coherence),先计算任意两列归一化内积,平均相干性定义为大于阈值t的所有内积的平均值,它能更好地反映稀疏表示行为和基追踪算法的性能.常见的能使A满足约束等距性的测量矩阵包括Gaussian矩阵[19],局部傅立叶矩阵[20]、二值随机矩阵[21]、局部哈达玛矩阵[22]、一致球矩阵[23]以及托普利兹(Toeplitz)矩阵[24]等.
1.2 压缩感知的稀疏重建模型
Candès等人证明若要精确重建原信号,可以通过求解最小l0范数的优化问题加以解决,基于压缩感知理论的重建模型可以写成如下的表达式[25]:

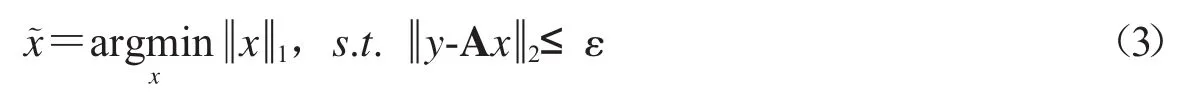
除了利用图像在变换域的稀疏性进行的最小l1范数的稀疏重建外,图像还可利用梯度的稀疏性进行稀疏重建,此时的稀疏重建模型转化为最小TV求解:
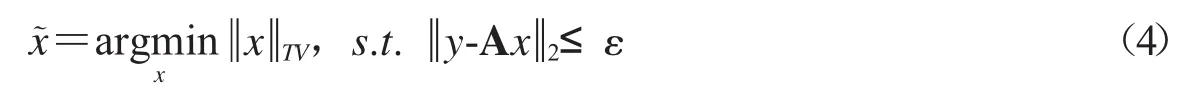
1.3 压缩感知的低秩重建模型
矩阵的低秩性是指矩阵的秩小于矩阵的行数或列数.基于此,研究人员将一维信号的最小化向量的范数扩展成二维矩阵的秩,创造出矩阵的低秩重建算法.
一个二维图形对应一个矩阵,令xi代表第i个位置处的向量,使用K近邻算法搜索出其第 i个位置处的 k 个相似向量,共同组成向量,由于Xi是由相似向量组成的,因此它有低秩特性.同时Xi又含有噪声,所以对二维图形建立模型Xi=Li+Ni,Ni代表高斯白噪声矩阵,Li代表低秩矩阵,秩最小化优化模型[27]如下:
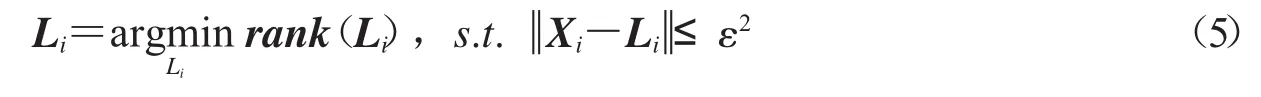
通常情况下,这个压缩传感重建问题的模型可以写成:


其中 L(Li,ε)是奇异值的对数和.
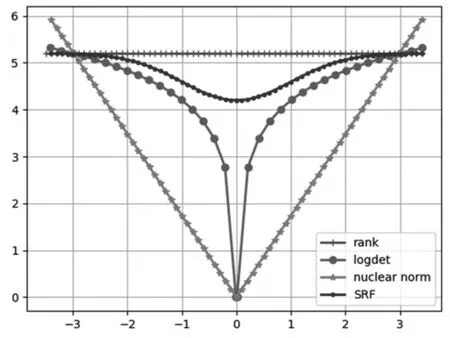
图2 不同函数对秩的逼近效果
扩展到三维数据的重建问题涉及到三维张量.建立起相应的重建模型之后,先对张量进行CP分解或者Tucker分解,使之变成二阶矩阵,进而依靠矩阵的恢复算法进行重构.以CP分解为例,三维的图像重建可以建立如下的模型:

1.4 压缩感知深度网络模型
近年来,随着神经网络和深度学习的快速发展,部分研究者借助神经网络结构构建了基于深度网络的压缩感知模型,西安交通大学构建的ADMM-CSNet[28-29]模型和北京大学的ISTA-Net[29]模型是两个典型的模型.这两个模型都是针对图像压缩感知重建设计的,本质上仍然是求解一个l1范数稀疏重建问题,求解模型[28]如下:

其中Dl表示某种稀疏或滤波变换,g(·)表示正则化函数,代表正则化参数,L是可能的分组信息.与传统压缩感知算法不同,这些参数在压缩感知网络模型中不需要提前设置,网络模型会计算出最优参数,且迭代次数远小于常规压缩感知的迭代算法[29-30].除此以外,Kuldeep等研究者提出了一种基于卷积神经网络结构的非迭代压缩感知快速重建算法ReconNet,它以图像的压缩感知随机测量值作为输入返回重建图像块[31].Mousavi[32]和Iliadis[33]结合分块压缩感知和全连接神经网络给出了全连接视频压缩感知模型.基于网络结构的压缩感知模型俨然成为了压缩感知重建的发展新方向.
2 压缩感知重建算法
重构算法一直以来是压缩感知理论实现的重点和难点.本文分别介绍稀疏重建模型和低秩重建模型两种不同模型下的各类重建方法.
2.1 稀疏信号的重建算法
2.1.1 凸优化算法
在稀疏重建模型中,Candès指出可以把复杂性和不稳定性较高的l0范数最优化问题转化为等价的l1范数最优化问题,通过不断寻找l1范数最小的来逼近我们压缩采样得到的信号y,当l1范数不再减少时,方程组求解成功.这种思路就引出了著名的基追踪方法(Basis Pursuit,BP),其计算复杂度为O(N3)[18].2007年,Figueiredo等人在梯度下降法的基础上提出了著名的稀疏梯度投影法(Gradient Projection for Sparse Reconstruction,GPSR),该算法受初始值的影响较小,而且通过调整正则因子可以有效提升算法的重建速度[34].除此以外,典型的凸优化算法还包括迭代收缩算法(iterative shrinkage thresholding algorithm,ISTA)[35]、快速迭代收缩算法(fast iterative shrinkage thresholding algorithm,FISTA)[36]、分裂 Bregman 迭代算法(Split Bregman Iteration,SBI)算法[37]和交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[38]等.
2.1.2 贪婪迭代算法
贪婪算法出现的时间较早,解决的是最小l0范数问题,求解时利用迭代算法通过减少残差寻找信号或图像的最稀疏表示.最典型的贪婪算法是匹配追踪算法(MP),由Mallat等人提出[39].随后,Troppj引入正交的思想,通过递归对己选择原子集合进行正交化以保证迭代的最优性,提出了正交匹配追踪算法(OMP)[40].为了缩小运算时间,提高重建精度,增强重建信号对噪声的鲁棒性,在2009年,Needell等人在OMP的基础上提出了正则正交匹配追踪(Regularized Orthogonal Matching Pursuit,ROMP)算法[41]和压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)算法[42].同年,Donoho等人提出了一种对稀疏度K自适应的稀疏自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)算法[43],可以在K未知的情况下获得较好的重建效果,速度也远快于OMP算法.
2.1.3 最小全变分法
最小全变分法求解的是公式(4)梯度稀疏问题.Candès等研究者从大量自然图像的离散梯度都是稀疏的角度出发,提出了针对图像重构的最小全变分法[44].
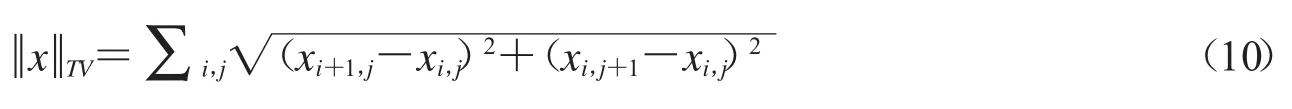
该问题的求解可以转换为二阶锥规划问题.最小全变分模型可以有效地解决图像压缩重构问题,重构结果精确而且鲁棒,但是运算速度较慢.
2.1.4 基于Bayesian框架的重建算法
基于Bayesian框架压缩感知重建算法着重处理时间相关性较强的信号.在Bayesian理论框架下,我们可以通过信号的稀疏表示得到信号的先验信息,通过压缩感知非线性采样得到信号的后验信息从而恢复原信号.2001年Tipping提出了结合稀疏贝叶斯学习和相关向量机(Relevance Vector Machine,RVM)学习算法对信号进行稀疏重建信号[45].2008年Ji S等人提出了一种Bayesian压缩感知(Bayesian Compressive Sensing)BCS算法[46].Bayesian压缩感知的相关算法还有Wipf在2004年提出的基于单测量向量的稀疏贝叶斯学习算法(Sparse Bayesian Learning,SBL)[47]和在2007年提出的基于多测量向量的MSBL算法[48].
2.2 低秩矩阵的重建算法
2.2.1 凸松弛法
凸松弛算法主要解决公式(5)和(6)的重建问题,Cai等人在2008年提出了SVT(Singular Value Thresholding)算法,该算法是基于线性伯格曼迭代(Linearized Bregman Iteration)的软阈值门限迭代收缩算法,但该算法的计算复杂度较高,收敛速度缓慢,且其重构解没有理论保证[49].2010年,Toh K.C.等人提出了NNLS(Nuclear-norm Regularized Least Squares)算法,该算法基于一种加速的近端梯度算法,用ε-最优解迭代,求解无约束核范数非光滑凸优化问题[50].同年,Mazumdar R等人利用核范数作为正则化子,提出了一个简单而有效的凸算法,即Soft-Impuse算法,它使重构误差在核范数上有界时达到最小,该算法软填充迭代替换丢失的元素与从软阈值SVD获得的那些元素[51].2012年,Wen等人提出LMAFit(Low-Rank Matrix Fitting)算法[52],该算法提出了一个低阶因子分解模型,并构造了一个非线性连续超松弛(SOR)算法,只需每次迭代求解一个线性最小二乘问题.大量的数值实验表明,LMAFit能够以比许多核范数最小化算法快几倍的速度可靠地解决各种各样的问题[53].
2.2.2 迭代阈值算法
低秩迭代阈值算法有迭代软阈值和迭代硬阈值两类算法,典型的算法包括SVP(Singular Value Projection)算法[54]、NIHT(Normalized Iterative Hard Thresholding)算法[55]和FPCA(Approximate SVD Based FPC Algorithm)算法[56]等.Jain P等人在2010年提出的SVP(Singular Value Projection)算法[54]属于硬阈值迭代算法,该算法将零矩阵作取为初始矩阵,用投影梯度下降法进行迭代更新,算法的收敛速度较快,对重构解的精确性也进行了详细分析,受采样值个数和原始矩阵的秩影响较小[54].2011年,Ma S等人利用同伦方法和近似奇异值分解过程,提出FPCA算法,该算法求解的是无约束版的核范数最小化问题[56].2013年,Tanner等人提出NIHT算法,它使用计算为精确地用于受限子空间的自适应步长,该方法被证明具有接近最优的从密集测量掩模恢复阶的保证,并且被观察到在某些方面具有优于用于密集测量掩模和进入测量的其它矩阵完成算法的平均情形性能[55].特别地,所提出的算法能够从非常接近所需的最小测量次数恢复矩阵[55].
2.2.3 贪婪追踪类算法
贪婪追踪类算法每次迭代时选取一个局部最优解来逐步逼近原始矩阵.2009年,Haldar和Hernando提出使用幂分解(PF)算法作为秩约束矩阵恢复的工具,提出了Incremented Rank Power Factorization算法[56].结果表明,增秩PF在恢复低秩矩阵方面明显优于核范数最小化(NNM),而且速度更快[56].2010年,Lee K等人对CoSaMP算法进行推广,提出了ADMiRA(Atomic Decomposition for Minimum Rank Approximation)算法[57].ADMiRA算法结构简单,计算量较小,并从理论上严格分析了重构解的精确性,但缺点是其受采样值个数和原始矩阵的秩影响较大[57].
3 结论与展望
压缩感知理论一经问世即得到广大研究者的青睐,目前压缩感知理论在通讯、图像处理、医学成像、生物传感等众多领域发挥着重要的作用.本文在阐述了压缩感知理论框架和重建模型的基础上,针对不同重建模型对压缩感知重构算法进行总结和评述.尽管研究者对压缩感知理论及重建算法的研究已经获得了很多有意义的成果,然而,随着新技术的产生与发展,将会不断涌现出更多的压缩感知模型和求解方法,如随着机器学习与深度学习模型在大数据处理中所展现的优势,使得压缩感知理论与深度学习网络结构的结合成为新的研究热点等.

