基于摆缸关节的液压机械臂运动学及工作空间分析*
罗中正,谢良喜,罗 刚,加 闯,李 昭
(武汉科技大学 机械自动化学院,武汉 430081)
0 引言
目前,由于传统机械臂的驱动关节大都采取电机与减速器相结合的形式,从而使得传统机械臂的负重比(即负载与自重之比)和功率-体积比非常小,负重比是衡量工业机器人性能好坏的重要指标之一。相比于电机传动,液压传动在相同功率下具有负载大、结构紧凑、传动平稳等突出优点, 其负荷-自重比具有显著优势。同时,输出功率的大小可以通过调节其系统压力进行控制。
美国波士顿公司推出的BigDog采用往复式直线液压油缸作为动力来源,借助液压系统的输出特性良好地满足了BigDog的动力需求[1-2]。夏磊[3]针对以摆动油缸作为驱动器的跳跃机器人进行了动力学仿真并求得了机器人运动轨迹,最后研制了样机进行实验。李贻斌[4]结合仿生学设计了一款液压驱动四足机器人,对其进行了运动学求解以及步态规划,最后通过实验验证了结构设计的合理性。高进芃[5]针对由液压摆动缸作为关节的机械臂,提出了与之对应的控制理论,制作样机并进行了相关试验。
可见国内外真正实现将关节型液压机械臂应用于搬运、码垛等场合并不多见。本文根据液压传动以及叶片式液压摆动油缸(摆缸)的优点,设计了基于摆缸关节的6自由度串联液压机械臂,主要适用于搬运和码垛重物的场合。由于摆缸体积小且质量轻,结构简单紧凑,而且油缸与臂杆之间不需要其他传动机构就能够实现直接驱动,所以该液压机械臂的突出优点是负重比大,传动平稳,机械损失较小,相比于传统机械臂优势十分明显。
针对本文设计的液压机械臂,通过改进的D-H法[6]对其进行运动学建模,推导出液压机械臂的运动学方程并对求出了正运动学的解析解,应用 MATLAB进行运动学仿真试验,最后运用蒙特卡洛法对其工作空间进行了分析计算,在MATLAB中绘制了与其对应的云图。
1 液压机械臂结构及连杆参数
以叶片式液压摆动油缸作为驱动关节,设计了基于摆缸关节的6自由度液压机械臂,整体的三维模型如图1所示。
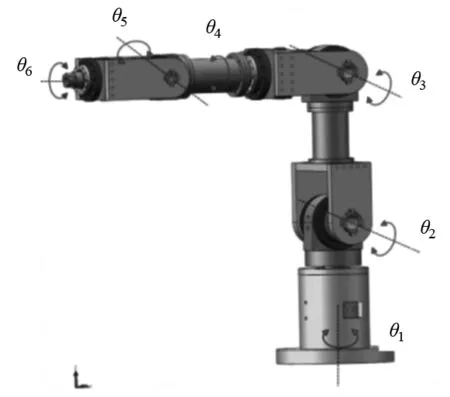
图1 机械臂整体模型
从图1可知,该液压机械臂共有6个关节,其中构成第一、二关节的两个摆缸相互垂直,称为模块化关节,同理,其余两组也是如此。模块化关节具有众多优势,其结构简单紧凑,集成度高,安装方便,大大降低了机械臂研发的复杂度以及制造成本,且有效地提高了机械臂的可维护性。同时,当机械臂工作空间的需求有所变化时,只需要更换不同长度的臂杆即可,简单便捷。
为了更加方便地描述机械臂各关节的实时位姿状态, 运用改进的D-H法得到与图1相对应的简化D-H坐标系。
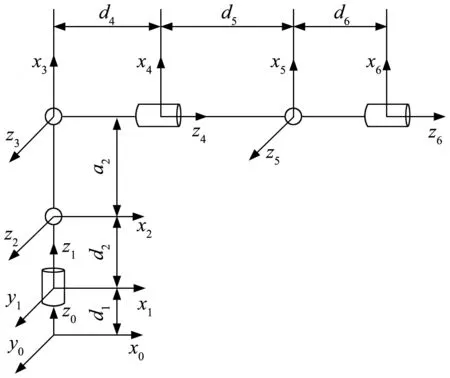
图2 液压机械臂D-H坐标系
图2中,ai为连杆长度,αi为连杆扭角,di为连杆偏置距离,θi为关节转角,只有θi是变量,其他3个均为定值。结合液压机械臂的实际尺寸得到其D-H参数表。

表1 液压机械臂D-H参数表
2 液压机械臂正运动学分析
运动学是从几何的角度来描述机械臂运动状态,对机器人技术具有重大意义,本文针对正运动学进行了讨论。正运动学是指已知各关节变量的确定值计算出末端相对于基座的位姿的过程,是机械臂工作空间求解的基础[7]。
当机械臂的D-H坐标系被规定好了之后,用位姿变换矩阵来描述相邻关节之间的关系:

(1)
式中,cθi=cos(θi),sθi=sin(θi),cαi-1=cos(αi-1),sαi-1=sin(αi-1)。结合表1和式(1),可得出各个相邻关节之间的位姿变换矩阵:
(2)
(3)
(4)
(5)
(6)
(7)
联立式(2)~式(7),可以得出末端点最终的位姿矩阵:
(8)
式中,[nxnynz]T,[oxoyoz]T,[axayaz]T表示的是末端执行器的姿态向量;[pxpypz]T则是位置向量。
取各个的关节角的初始值为θ1=θ2=90°,θ3=θ4=θ5=θ6=0°,解得该液压机械臂初始位姿:
(9)
式(9)所表达的位姿状态和图2坐标系中所示状态一致,证明文中建立的正运动学方程是正确的。
3 正运动学仿真
3.1 模型建立
在MATLAB中使用robotics toolbox来创建所设计液压机械臂的三维仿真模型,使用link语句 :
L=([alphaAthetaDSigma],′modified′)
(10)
alpha、A、theta、D依次代表连杆扭角、连杆长度、关节变量以及连杆偏置距离,Sigma=0表示只有转动副没有移动副,modified表示采用改进的D-H法。

图3 液压机械臂仿真模型
从图3可以看出,根据表1中的参数建立的液压机械臂仿真模型与图1完全相符,再次证明对液压机械臂的D-H建模是正确的。
3.2 机械臂轨迹规划仿真
在MATLAB中采用jtraj语句进行液压机械臂的轨迹规划:
[qqdqdd]=jtraj(qA,qB,t)
(11)
式中,q是从初始状态qA到最终状态qB的关节轨迹,qd与qdd分别表示的是关节角的速度和加速度,t是运动时间。
以本文设计的液压机械臂为例进行仿真,规定末端执行器从A点运动到B点,设定各关节初始角度为[pi/2pi/20000],最终关节角度为[00pi/2pi/2pi/2pi/2]。

图4 末端执行器运动轨迹

图5 液压机械臂末端执行器坐标投影
从图4和图5分别为机械臂末端执行器的运动轨迹及其位移变化曲线,可以看出坐标曲线变化较为平缓,即可以平稳地到达预定位置。
此外,通过轨迹规划仿真还可以得到该液压机械臂任意关节角的特性曲线。由于关节1和关节2运动规律一样,其余4个关节运动规律一样,所以此处只给出了关节1和关节3的角位移等随时间的变化规律曲线,如图6和图7所示。可以看出该液压机械臂关节角位移等变化都比较平缓,无明显突变,说明该液压机械臂在运行过程中各关节运转都比较平稳,从而证明此结构设计合理。

图6 关节1转角特性曲线

图7 关节3转角特性曲线
4 液压机械臂工作空间分析
机械臂末端执行器运动描述点能够到达的所有位置构成的集合就是其工作空间,它是权衡机械臂性能好坏的重要依据之一,对于机械臂的结构参数优化等方面具有深远意义[8]。国际上众多学者针对机械臂工作空间的求解进行了大量的研究,并且提出了许多计算方法,目前比较常用的有数值法、解析法、图解法和 蒙特卡洛法。
蒙特卡洛法借助随机数来解决问题,由于其可以借助计算机进行模拟,所以计算速度快且便捷,能够在计算机中精确地绘制出图形,大大地减少了计算量,具有不受关节数量限制的优势。同时,蒙特卡洛法得到的结果的准确性与实验次数成正比,只要实验次数足够多,结果就无限接近于准确值。因此,本文应用蒙特卡洛法进行分析计算[9-11]。其计算流程如图8所示。
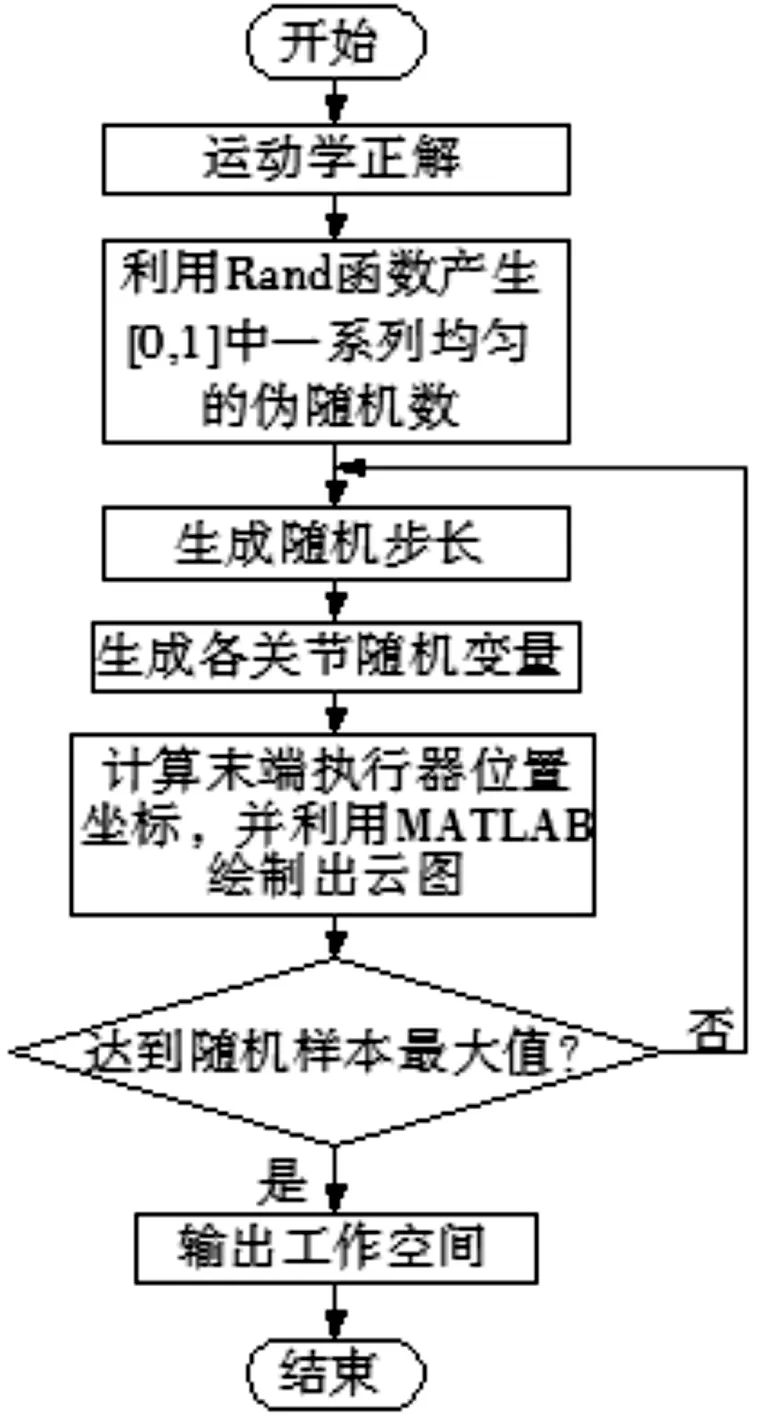
图8 算法流程图
其中,随机步长的计算方法为:
(12)
各关节的随机变量的计算方法为:
(13)

图9 三维空间云图
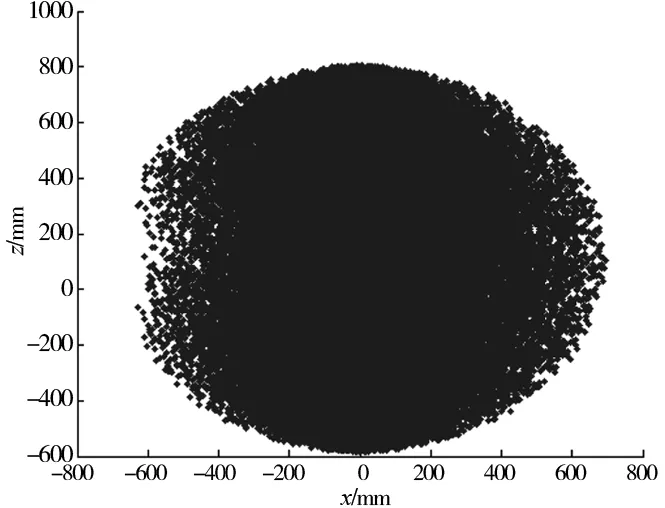
图10 xoz平面投影视图

图11 yoz平面投影视图
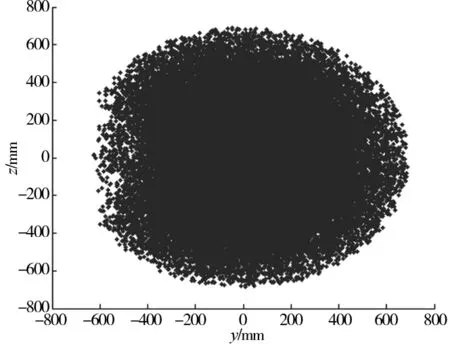
图12 xoy平面投影视图
从图10~图12可以得出该液压机械臂的工作空间范围是:x∈[-630,700]mm,y∈[-700,700]mm,z∈[-600,800]mm。
5 结束语
设计了基于摆缸关节的六自由度液压机械臂,采用改进的D-H法建立了该液压机械臂的坐标变换矩阵,得到了其正运动学方程。在MATLAB中创建了液压机械臂仿真模型并对其正运动学进行了仿真,得到的关节特性曲线较为平滑,证明该液压机械臂结构设计是合理的。应用蒙特卡洛法对该液压机械臂工作空间进行了计算与仿真,得到了与其对应的云图,为今后对液压机械臂的进一步研究提供了重要依据。

