高速电主轴电磁振动噪声多场耦合分析*

吴玉厚，于海涛，张峰铭

(沈阳建筑大学 机械工程学院,沈阳 110168)

0 引言

高速电主轴在正常运转时，不可避免的会产生振动和噪声，进而影响到电主轴的动态特性。经分析可知，电主轴的振动可以分为电磁振动、机械振动、气体振动这三部分。随着现代工艺的不断改进，机械振动和气体振动已经有了明显的改善，但由于电磁振动的产生因素比较复杂且受到电主轴内部电机结构的限制，所以依然是影响电主轴动态特性的一个重要因素，亟待抑制和改善。

国内外对电主轴电磁场、电磁振动和电磁噪声都有过相应的研究，孙雪等[1]对高速异步电主轴电机进行了电磁振动和声场分析,并计算出电机在空载和负载情况下产生的电磁噪声。郭桦等[2]通过实验研究了陶瓷电主轴的电磁振动特性。何海波等[3]建立了异步电机径向电磁力的计算模型，关注了可能出现的电磁力的频率，采用有限元方法验证了解析磁场计算的正确性。李岩等[4]和王玎等[5]都利用了磁固耦合振动理论分别对三相异步电机进行了相应的电磁振动分析。Ishibashi等[6]分析了感应电机内部产生的谐波电磁力，指出电磁振动是中小型电机振动的主要来源。Ciprian Gheorghe Nistor等[7]用有限元方法分析了绕组形式对电机电磁振动的影响。Hirotsuka等[8]利用实验研究了三相异步电机空载电磁振动及噪声的径向分布情况。虽然上述学者对电机电磁场、电磁振动和电磁噪声分别进行了深入的研究，但并没有把磁场、振动和噪声结合起来进行多场耦合的系统性分析。

本文利用有限元分析法对电主轴的电磁特性及其对主轴振动和噪声的影响进行了分析，并结合电主轴噪声实验进行验证。首先在ANSYS Maxwell中建立电主轴电机二维有限元模型，分析在瞬态电磁场下，电主轴在给定转速稳态运行状态下的磁场分布和作用在定子上的时变电磁力；接着在ANSYS Workbench中，将二维瞬态场得到的瞬态电磁力作为结构谐响应分析的谐载荷，并作用在电主轴的定子齿表面上，得到电主轴在正常运行时的电磁振动的响应规律，同时在噪声模块中分析出电主轴电磁振动所产生的声场特性；最后进行电主轴噪声实验，提取出主要的电磁噪声信号，并得到电磁噪声的最大噪声响应频率，与仿真得到的电磁噪声结果进行对比。结果表明，电主轴的电磁振动噪声多场耦合可以合理的分析出电主轴电磁场对主轴的振动和噪声的影响，也为以后电主轴电磁参数的设计和优化提供理论依据。

1 电主轴电磁场分析

电主轴电磁振动噪声多场耦合分析的主要流程[9]，如图1所示。

图1 电主轴电磁振动噪声分析流程

按照图1的仿真流程，在对电主轴电磁场分析时需要计算出电主轴的电磁力。根据以往的分析可知，产生电主轴电磁振动的主要因素是磁场中相互作用产生的径向力，所以将径向电磁力作为主要研究对象。依据麦克斯韦应力张量法，单位面积上的径向电磁力的瞬时值[10]可以表示为：

(1)

式中，u0—空气的磁导率；u0=4π×10-7H/m；br—径向磁通密度。

本研究以型号是170SD30-SY的电主轴为仿真对象，其主要结构参数为：电机极数2p=4，定子槽数Z1=24，转子槽数Z2=28，定子外径130mm，定子内径80mm，转子外径79.4mm，转子内径51mm，建立的二维电主轴有限元模型，见图2。

图2 电主轴二维瞬态场有限元模型

在Maxwell平台中，为了准确的计算出气隙磁场作用在定子上的电磁力，在划分网格时要对原有的二维几何模型进行优化调整，将定子齿部分分离出来进行网格细分、调整时间步长、开启谐响应力学计算命令，以便将数据导入到ANSYS软件中对定子铁芯进行电磁振动的响应分析。

本研究采用时步有限元法，仿真分析电主轴在24000r/min 运行时磁场变化的规律。通过求解及数据处理得到电主轴在0.04s时气隙径向磁密沿周向的变化曲线，如图3所示。

图3 电主轴气隙径向磁密分布图

从图3可以看出，电主轴的气隙磁密分布大体上呈近似正弦曲线分布。气隙磁密分布存在两个相同的波峰和波谷，大小分别为0.6T和-0.6T。同时，运用麦克斯韦应力张量法计算得到电主轴在沿周向分布的径向电磁力变化情况，并对其进行空间傅里叶分解，见图4。

图4 电主轴电磁径向力分布

从图4可知，电主轴运行时径向电磁力的分布是周期性的，沿一个周向有4个周期变化，且产生的4个径向力波峰大小是相等的，所以理论上是不会存在不平衡磁拉力的。

2 电主轴电磁振动分析

2.1 定子模态分析

对定子固有频率的研究是研究电主轴振动中的一项，为了避免在做振动试验时电主轴产生共振，需要在定子振动谐响应分析之前计算定子的固有频率，分析其各阶模态。由于主要关注定子的径向模态，因此定子仿真计算模型主要按照定子径向模态的振型进行提取。有限元仿真时定子铁芯选用的材料为硒钢片，弹性模量为195GPa，泊松比为0.25，密度为7650kg/m3。

定子结构为2～5阶的径向模态振型,如图5所示。

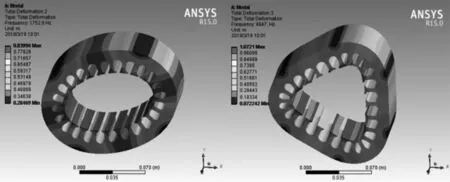
(a)m=2 (b)m=3

(c)m=4 (d)m=5 图5 定子2～5阶径向模态振型

由图5可知，定子模型的2阶固有频率为1752.9Hz，此时的径向模态振型是椭圆形，随着阶次的升高，相应的固有频率也随之增加。3阶、4阶和5阶的固有频率分别是4647Hz、8162.7Hz和11531Hz，其对应的径向模态振型分别是三角形、四边形和五边形。

2.2 定子电磁振动谐响应分析

由于谐响应分析可以同时计算一系列不同频率和幅值的载荷所引起结构的响应，所以在本研究中对电主轴定子振动特性的分析时采用谐响应分析。按照电主轴电磁振动响应分析流程，将式(1)作为结构谐响应分析的谐载荷，计算电主轴电磁振动的响应。

在谐响应分析中，建立电主轴结构振动的微分方程为：

(2)

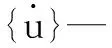
在做电主轴的振动特性分析时，由于电主轴转子为实心柱状结构，刚度较大，不容易变形，相对电主轴的定子来说，径向电磁力对主轴转子的作用不明显，因此忽略电主轴转子的影响，主要针对电主轴定子进行电磁振动分析。

本仿真研究的电主轴定子振动特性主要考虑定子的径向振动，故可以在做谐响应分析时将定子结构简化为二维模型再进行有限元分析。图6是以时域瞬态电磁场分析得到的稳态电磁力作为激励源加载到定子齿表面进行谐响应分析时定子各个齿面电磁力的分布情况。

图6 定子受力分布图

图7为在0～10000Hz的频率范围内，在恒幅激励力的作用下，电主轴某个定子齿部的变形随激励频率的变化曲线。

图7 定子齿部变形随激励频率的变化

由图7可以看出，随着激励力频率的增加，电主轴定子齿部振动都呈下降趋势，所以在研究电主轴的电磁振动时，应着重考虑低频范围内电磁力的作用。实际上电主轴定子在低频范围内和高频范围内的振动形式是不同的。在低频范围内，定子主要呈现出整体的变形，而在高频范围内，电机定子整体变形较小，局部变形较大，这一点也可以从定子的径向模态振型中可以看出来。为了进一步探讨偏心对定子电磁振动的影响，表1选取了在低频范围内4种激励频率下的定子结构的最大振动位移。

表1 不同激励频率下定子结构最大振动位移

结合表1和图7可以看出，在这4种激励频率下，在接近定子2阶固有频率时，电磁振动造成定子结构的变形为0.434mm，这是在所有激励频率中产生的最大的振动变形，说明当激励频率在接近定子2阶固有频率时，电磁力波会与定子铁心发生共振，产生较大位移。

3 电主轴电磁噪声分析

在电主轴定子电磁振动响应仿真模型的基础上，引入噪声Acoustic模块，进而计算出电主轴的电磁噪声。通过建立圆柱面空气域噪声辐射模型，使空气域模型内表面与定子外表面相重合，空气域外表面设置为辐射表面，并将上面研究的电主轴定子电磁振动响应模型作为噪声激励源进行分析。由谐响应分析可知，定子电磁振动响应最大幅值频率在1750Hz附近，故取电主轴定子在1750Hz下的的电磁噪声声压和声压级仿真结果，如图8所示。

(a)电磁噪声声压 (b)电磁噪声声压级 图8 1750Hz处电磁噪声声压及声压级仿真结果

由电主轴电磁噪声声压及声压级云图可以看出，电主轴在无偏心时产生的电磁噪声沿周向分布均匀，且主要噪声分为4个方向，经分析声压分布与二阶模态振型一致。选取电主轴定子外表面处进行噪声分析，得到声压随频率的变化如图9所示。从曲线中可以看出，电磁噪声在13750Hz声压压强最大。

图9 电主轴定子外表面声压响应图

4 电主轴噪声实验

对同型号的电主轴进行电磁噪声实验，实验平台如图10所示，左图为噪声信号采集及处理设备，右图为实验主轴及噪声检测平台。6个传感器采集电主轴的不同位置的噪声信号，并将噪声值传送给信号采集仪进行信号处理，其中第1传感器和第6传感器分别检测电主轴前端和后端位置的噪声，而第3传感器测量的是电主轴中间位置的噪声信号。据分析可知，测得的电主轴噪声主要有机械噪声，电磁噪声和气体噪声，而电主轴运行时的噪声源主要有电主轴前后两端轴承位置以及电主轴中间定转子气隙磁场位置。

图10 电主轴噪声实验测试平台

实验时，测得在24000r/min时电主轴运行时的噪声声压频谱图如图11所示。

(a)第1传感器

(b)第3传感器

(c)第6传感器 图11 电主轴噪声声压频谱图

对比3个位置噪声频谱图可以看出，三个位置测得的噪声声压峰值随声压频率变化基本相同。然而第3传感器测得的声压在13800Hz处有较大峰值，而其他两处传感器在此频率处的峰值相对较小，根据声源定位原理，此频率下的声压峰值主要产生于电主轴的电磁场，即为电磁噪声，这与仿真出的电磁噪声声压峰值频率13750Hz近似，验证了上述仿真结果的准确性。

5 结论

本文通过实验与仿真相结合的方法，研究电主轴电磁场特性对主轴振动及噪声的影响，然后通过电主轴噪声实验，提取出主要的电磁噪声信号并与仿真结果进行对比，得出以下结论：

(1)由电主轴定子振动的谐响应分析可知，当激励频率接近于定子2阶固有频率时，电磁力对定子结构变形的影响最大，即电磁力波与定子铁芯二阶固有频率接近时，产生的振动最大。

(2)由电磁噪声仿真声压图并结合电磁噪声实验可以看出，当电主轴运行转速为24000r/min时，电磁力产生的最大噪声声压频率为13800Hz。

(3)通过实验和仿真对比，可以验证电主轴电磁振动噪声多场耦合的分析方式具有一定的合理性和准确性。