整体叶盘叶片砂带磨削加工振动数值仿真研究

梅 科，刘 颖，金 华，肖贵坚

(重庆大学 机械工程学院，重庆 400044)

0 引言

整体叶盘是现代航空发送机的关键零件，其加工质量直接影响航空发动机的性能。但整体叶盘具有叶片薄壁弱刚性、叶片间通道狭长、型面为自由曲面及材料难加工等特点[1]，导致其表面精密加工十分困难。

目前，采用新型开式砂带磨削技术可以适应整体叶盘的结构和材料特点[2-3]。但是，在磨削过程中出现让刀、振动等问题，严重影响了加工后工件的几何精度及表面质量。因此，研究整体叶盘砂带磨削过程中的振动机理及其抑制方法对于改善整体叶盘表面加工质量具有重要意义。建模与仿真最终是为了实现对磨削结果的预测、对磨削条件的优化及对磨削过程的控制。磨削过程的建模主要包括经验建模、理论建模及数值模拟建模三种方式[4]。

国内外学者对于磨削数值仿真做了大量的研究， J C Aurich等根据几何运动仿真得到磨削过后的工件形貌与动态磨削力[5]。宿崇等分析了磨粒的切削机理及工件表面的创成机理[6]。刘月明等建立了对应分布规律的球形磨粒砂轮三维数值模型[7]。F Klocke基于有限元法对单颗磨粒磨削的微观形貌进行了研究[8]。R Rentsch等[9]通过分子动力学方法进行了单颗磨粒切削过程仿真研究。Hoffmeister等[10]研究了不同冷却条件对磨削加工工件表面的影响。K Weinert等[11]研究了不同工艺参数下的温度分布情况，可为实际加工工艺条件的选择提供参考。

但国内外学者针对整体叶盘叶片型面砂带磨削过程中由于工艺参数选择不当而带来的振动问题，并未做相关深入研究，本文基于理论建模和数值仿真方法展开研究，探索整体叶盘砂带磨削振动的影响因素及稳定磨削条件。

1 整体叶盘砂带磨削动力学模型

为了研究整体叶盘叶片型面砂带磨削过程中的振动机理，首先建立磨削过程中的动力学模型，设磨削过程中工件与接触轮之间的接触刚度为kcb(kc为单位宽度上的接触刚度)，柔性接触轮刚度为kf。整体叶盘叶片型面砂带磨削过程中的动力学模型如图1所示。

图1 整体叶盘砂带磨削动力学模型

磨削过程中的位移方程为：

δw(t)+δb(t)=ap(t)-yg(t)-yw(t)-yc(t)

(1)

其中，δw(t)为任一瞬时工件的有效磨削量；δb(t)为任一瞬间的砂带磨损量；ap(t)为磨削深度；yg(t)为接触杆的弹性变形；yw(t)为工件的弹性变形；yc(t)为接触变形。

磨削进给量、工件的有效磨削量、砂带磨损量的增量方程为：

(2)

其中，τw为工件的时滞。

接触杆柔度和接触区变形方程：

(3)

其中，kge为接触杆结构等效静刚度；Gg(t)为接触杆结构动柔度；kc为接触刚度；kwe为工件等效静刚度；Gw(t)为工件结构动柔度。

将式(1)、式(2)、式(3)进行Laplace变换可得：

(4)

令该磨削系统传递函数G(s)的分母为0，可得到系统的特征方程：

(5)

设法向磨削力方向的振动频响传递函数为G(ω)，振动的同相和不同相部分分别由其实部和虚部表示，因此：

G(ω)=GR(ω)+iG(ω)

(6)

根据定义，则系统的振动响应为：

y(t)=G(ω)Pn=G(ω){Rb[-y(t)+y(t-τ)]}

(7)

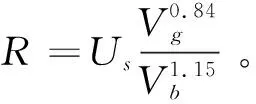
将式(6)带入式(7)，整理化简可得：

(8)

Tlusty提出在稳定性边界条件下，y(t)和y(t-τ)的模大小相等，即：

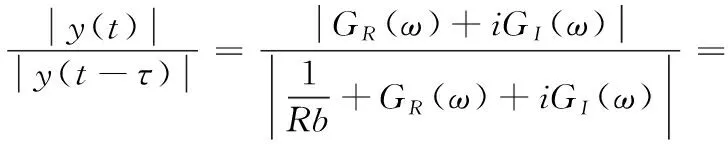
(9)

上式两端平方并化简可得稳定边界下的磨削宽度：

(10)

由于磨削宽度为正，所以GR(ω)为负，稳定边界下的最小磨削宽度blim由最大的同向频响传递函数GR,max(ω)决定。所以：

(11)

(12)

将R和GR,max(ω)带入公式(12)并化简可得：

(13)

由上式可知，整体叶盘砂带磨削稳定性极限受砂带线速度、进给速度、磨削正压力、接触轮硬度等工艺参数的影响。

2 磨削仿真方案

整体叶盘砂带磨削稳定性同时受多种工艺参数的影响，若进行全面试验，试验规模较大，由于试验条件的限制难于实施。因此，采用正交试验方法。本仿真采用4因素3水平的正交表L3(34)，重点分析砂带线速度Vb(A)、磨削正压力Fn(B)、进给速度Vg(C)及接触轮硬度(D)对整体叶盘叶片型面磨削振动的影响规律，设计因素水平如表1所示。

表1 整体叶盘砂带磨削仿真因素水平表

根据正交试验方法可知，一共需要进行9组磨削仿真试验，此外，试验中用到的其他相关参数，如砂带长度、砂带宽度、接触轮宽度和接触角度等如表2所示。

表2 整体叶盘砂带磨削仿真参数表

3 基于ABAQUS的磨削仿真过程

3.1 几何建模及网格划分

3.1.1 工件几何建模与分网

选择模型类型为3D可变形体，通过拉伸的方式可直接生成工件几何模型。为了缩短计算时间，只取宽度为0.84mm工件作为仿真对象。如图2a所示仿真对象取样，如图2b所示工件模型分割。

(a)仿真对象取样 (b)工件模型分割 图2 工件模型

3.1.2 接触轮几何建模与分网

接触轮模型为空心圆柱体，结构规则，只取宽度为0.84mm的模型作为仿真对象。

接触轮分网。设定所有单元为显示计算的8节点六面体线性减缩积分单元(C3D8R)。划分完成后的接触轮网格如图3a所示。

(a)接触轮几何模型 (b)单颗磨粒几何模型 图3 接触轮网格与磨粒

磨粒建模。在Abaqus/CAE中创立磨粒模型，由于磨粒材料硬度很大，仿真中将其按刚体处理。为了便于与接触轮进行接触对设置，将磨粒底部用接触轮外径大小的圆柱面切除，完成后的金字塔砂带磨粒模型如图3b所示。

磨粒分网。磨粒直接用离散刚体模拟，每个面只划分一个网格，单元类型选择离散刚体单元R3D3，以加快计算速度。

3.2 定义模型材料属性

接触轮选用的材料为丁晴橡胶，对于橡胶类物理非线性材料，常用Mooney-Rivlin模型来描述。对于2参数的Mooney-Rivlin模型其应变能密度函数的表达式为：

W=C10(I1-3)+C01(I2-3)

(14)

其中，W为应变势能；I1、I2为变形张量；C10、C01为Rivlin系数[12-13]，均为正定常数，由试验确定。实验得到硬度为75Hs/A的接触轮的Mooney-Rivlin参数如表3所示。

表3 接触轮材料Mooney-Rivlin参数

整体叶盘的材料为钛合金材料TC4，该材料具有强度高、耐热性好、密度小等特点，由光滑试件的准静态拉伸试验可获得其弹性参数如表4所示。

表4 整体叶盘材料的弹性参数

本文研究选用砂带磨粒材料为立方氮化硼(CBN)。其材料属性如表5所示。

表5 砂带磨粒的材料属性

3.3 装配与接触定义

材料属性定义好之后就进行如下操作：

(1)模型装配。首先，在Assembly模块中引入工件、接触轮和磨粒模型，通过平移和旋转方式将接触轮定位于工件上的适当位置。

(2)磨粒与接触轮之间固定约束。接触间隙容差根据模型尺寸设为0.001mm；搜索实体的几何特征设定为只搜索圆弧面；Rules设为当模型间隙不超过0.001mm时生成tie。

(3)磨粒与工件的接触定义。将磨粒表面和工件材料的结点区域做surface to surface接触，设定接触属性为Tangential Behavior，Friction formulation选择为Penalty，摩擦系数设为0.2。

(4)Connector单元设置。首先，基于三个参考点(RP-2，RP-3，RP-3)生成两个connector线段，Wire 1和Wire 2。然后，定义截面属性，Wire 1类型选择translator，并赋予弹簧阻尼属性；Wire 2类型选择Hinge。最后，把截面属性赋予线段完成connector的定义。Connector定义如图4所示。

图4 Connector定义

(5)运动耦合。建立一个couple，把参考点和实体联系起来。选择将接触轮端面(对称面)上的参考点和接触轮实体做运动耦合。

3.4 边界条件与载荷

(1)边界条件定义。

接触杆运动定义为沿X方向平移20mm，并通过Amplitude定义其进给速度的大小。如表6所示，通过改变时间参数可以定义不同的进给速度，该时间和分析步中的时间相等。

表6 进给速度定义方法

转轴运动定义为绕坐标轴Z轴的角速度为工艺方案对应值，其余自由度不加限制。此外，为了防止从0开始做进给运动出现不收敛的情况，通过Predefined Field为接触轮定义初始速度Vg0=200。

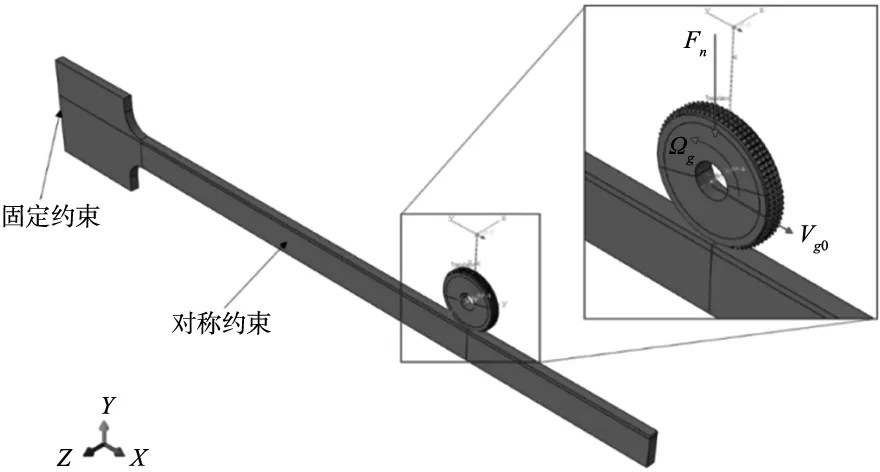
图5 边界条件与载荷定义

(2)载荷定义。由于力加载模式容易引起接触反弹，因此，选择位移加载模式。位移加载模式即将磨削正压力转换为磨削深度，在装配中直接将接触轮按磨削深度压入工件，并限制住接触杆顶端的Y向移动自由度。载荷定义如图5所示。

4 磨削仿真结果与分析

4.1 磨削后工件形貌

不稳定边界条件下，工件的磨削深度越来越浅(图6a)，这主要是由于沿走刀方向工件刚度越来越小，受力变形越来越大，工件的变形逐渐抵消了位移加载，使得工件与刀具脱离接触，计算终止。而在稳定边界条件下，刀具与工件时刻保持良好接触关系，使得工件在整个磨削过程中的磨削深度保持一致，如图6b所示。因此，在数值仿真中，为了保证仿真能够进行下去，应该定义工件为稳定的边界条件。

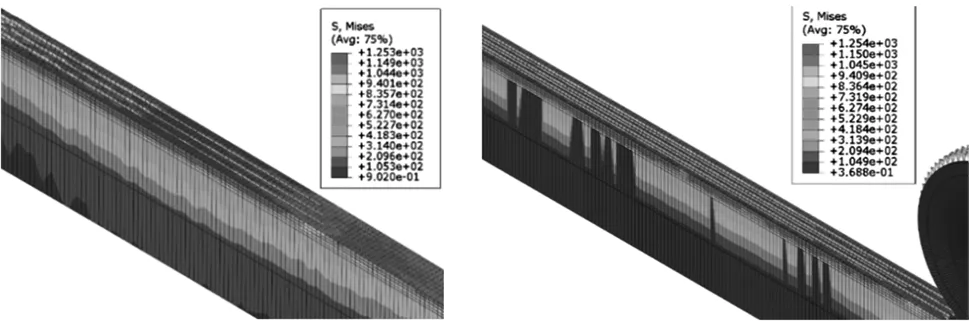
(a)不稳定边界 (b)稳定边界 图6 磨削后工件表面形貌

4.2 法向磨削反作用力

在稳定边界条件下，按位移加载模式得到的9组正交仿真试验结果(法向磨削反作用力)如图7所示。

图7 法向磨削反作用力

4.3 仿真结果分析

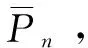
(15)

Psd越大，表明工件表面所受法向磨削力变化越大，磨削过程越不稳定。反之就越稳定。正交仿真试验结果对应的指标运算结果如表7所示。

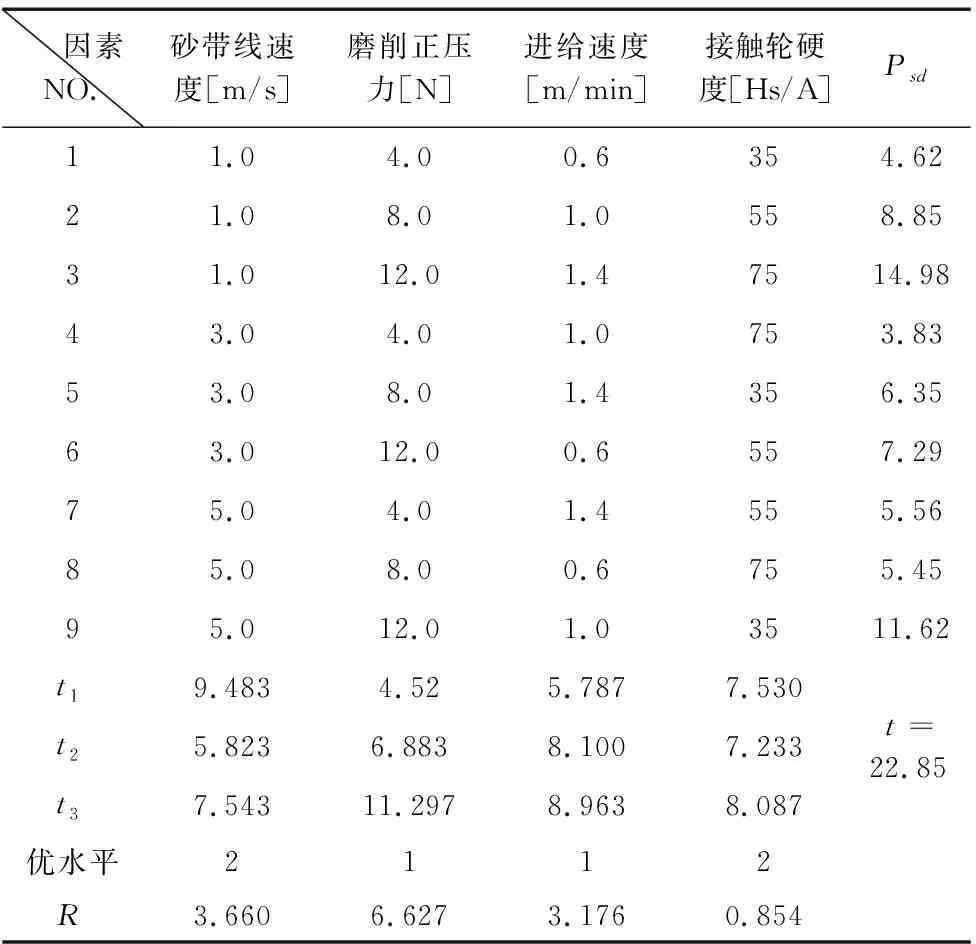
表7 正交仿真试验结果运算分析表

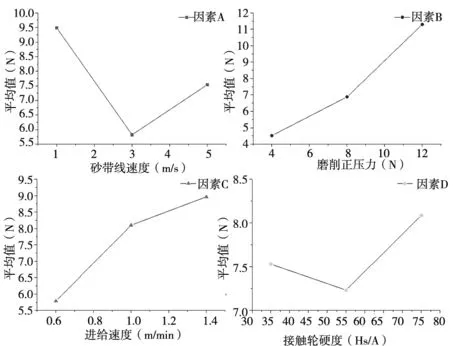
图8 因素与指标趋势图

R表示极差，反映了各列因素的水平变动时，试验指标的变动幅度。R越大说明该因素对试验指标的影响越大，因而也更重要。由表9可得各影响因素的主次顺序为：磨削正压力>砂带线速度>进给速度>接触轮硬度。

5 结论

研究表明，整体叶盘叶片砂带磨削的加工振动稳定性受砂带线速度、磨削进给速度、磨削压力、接触轮硬度、接触宽度等工艺参数的影响。按影响程度排序依次为：磨削正压力，砂带线速度，进给速度和接触轮硬度。随着砂带线速度的增加，磨削稳定性先增大后减小；随着磨削正压力的增加，磨削稳定性逐渐减小；随着进给速度的增加，磨削稳定性逐渐减小；随着接触轮硬度的增加，磨削稳定性先增大后减小。