广义四参数Birnbaum-Saunders疲劳寿命分布密度函数的图像特征

王蓉华，顾蓓青，徐晓岭

（1.上海师范大学 数理学院，上海 200234；2.上海对外经贸大学 统计与信息学院，上海 201620）

0 引言

Birnbaum-Saunders模型是概率物理方法中的一个重要失效分布模型，这个模型是Birnbaum和Sauders于1969年在研究主因裂纹扩展导致的材料失效过程中推导出来的，这一模型在机械产品可靠性研究中应用广泛，主要应用于疲劳失效研究，对于电子产品性能退化失效分析也有重要应用。

设X服从两参数Birnbaum-Saunders疲劳寿命分布BS(α，β)，其分布函数F(x)与密度函数分别为：

其中，α＞0称为形状参数，β＞0称为刻度参数（或者称为尺度参数），φ(x)，Φ(x)分别为标准正态分布的密度函数与分布函数，即：

由于Birnbaum-Saunders疲劳寿命分布是从疲劳过程的基本特征出发导出的，因此它比常用寿命分布如威布尔分布,对数正态分布更适合描述某些由于疲劳而引起失效的产品寿命规律。此分布已经成为可靠性统计分析中的常用分布之一。

已有众多的文献对两参数Birnbaum-Saunders疲劳寿命分布BS(α，β)进行了研究[1-7]，值得指出的是，Owen[8]首次提出一种广义三参数BS疲劳寿命分布，在此记为GBSI(m，α，β) ，其 分 布 函 数 的 形 式 为 ：F(x)=Φ其后 Diaz-Garcia等[9]、Fierro等[10]也都对GBSI(m，α，β)分布作过初步研究，Chacko等[11]专门对GBSI(m，α，β)分布作了研究，画出了该分布密度函数的图像，讨论了其简单的性质，并写出了似然函数的形式。Owen[12]也提出了一种新的广义三参数BS疲劳寿命分布，在此 记 为GBSII(m，α，β)，其 分布函 数 的形式 为 ：，研究了参数的点估计，其涉及到一个复杂的二元超越方程的求解问题。

本文提出一种广义四参数BS疲劳寿命分布GBS(m1，m2，α，β)，研究了该分布的性质及密度函数的图像特征。

1 广义四参数Birnbaum-Saunders疲劳寿命分布GBS(m1,m2,α,β )

设非负随机变量λ(x)服从广义四参数Birnbaum-Saunders疲劳寿命分布GBS(m1，m2，α，β)，其分布函数f(x)与密度函数分别为：

其中，x＞0，α＞0，β＞0，m1＞0，m2＞0

特别地，（1）若取m1=m2=m，β′=β1/(2m)，此时

参数BS疲劳寿命分布GBSI(m，α，β′)。

（2）若取m1=1-m，m2=m，0＜m＜1，此时F(x)=Φ即为文献[12]中的广义三参数BS疲劳寿命分布GBSII(m，α，β)。

（3）若取m1=m2=0.5，即为两参数BS疲劳寿命分布BS(α，β)。

定理1：设X～GBS(m1，m2，α，β)，其分布函数、密度函数分别记为F(x)，f(x) ，记Y=X-1，则：（1）Y～GBS(m2，（3）密度函数f(x)的图像特征为“单峰”（即“倒浴盆”形）或“双峰”（即“M”形），也有可能呈“三峰”。

2 分情况讨论

（1）若g2(y)≤0，g′1(y)≤0时

由此，f(x)的图像是“先严格单调增加后严格单调下降”，即呈“倒浴盆”形。

由此，f(x)的图像是“先严格单调增加后严格单调下降”，即呈“倒浴盆”形。

（a）当g1(y)≤0时，g′(y)≤0，易见f(x)的图像是“先严格单调增加后严格单调下降”，即呈“倒浴盆”形。

（b）存在y11，y12，y11＜y12有g1(y11)=g1(y12)=0 时，当0＜y＜y11时 ，g1(y)＜0 ，g′(y)＜0 ；当y11＜y＜y12时 ，g1(y)＞0，g′(y)＞0；当y＞y12时，g1(y)＜0，g′(y)＜0

若 存 在y0有g(y0)=0 ，当 0＜y＜y0时 ，g(y)＞0，f′(x)＞0 ；当y＞y0时，g(y)＜0，f′(x)＜0 ，即f(x)的图像是“先严格单调增加后严格单调下降”，呈“倒浴盆”形 。 若 存 在y01，y02，y03，y01＜y02＜y03有g(y01)=g(y02)=g(y03)=0 ，当 0＜y＜y01时 ，g(y)＞0，f′(x)＞0 ；当y01＜y＜y02时 ，g(y)＜0，f′(x)＜0 ；当y02＜y＜y03时 ，g(y)＞0，f′(x)＞0；当y＞y03时，g(y)＜0，f′(x)＜0

则f(x)的图像是“先严格单调增加再严格单调下降后严格单调增加最后再严格单调下降”，呈“M”形，f(x)具有“双峰”特征。

（a）存 在y1有g1(y1)=0 ，当 0＜y＜y1时 ，g1(y)＞0，g′(y)＞0 ；当y＞y1时，g1(y)＜0，g′(y)＜0 ，则f(x)的图像是“先严格单调增加后严格单调下降”，即呈“倒浴盆”形。

（b）存 在y11，y12，y13，y11＜y12＜y13有g1(y11)=g1(y12)=g1(y13)=0 时，当 0＜y＜y11时，g1(y)＞0 ，g′(y)＞0 ；当y11＜y＜y12时 ，g1(y)＜0，g′(y)＜0 ；当y12＜y＜y13时 ，g1(y)＞0，g′(y)＞0 ；当y＞y13时，g1(y)＜0，g′(y)＜0

若存在y0有g(y0)=0，当 0＜y＜y0时，g(y)＞0，f′(x)＞0 ；当y＞y0时，g(y)＜0，f′(x)＜0，即f(x)的图像是“先严格单调增加后严格单调下降”，呈“倒浴盆”形。若存在y01，y02，y03，y01＜y02＜y03有g(y01)=g(y02)=g(y03)=0 ，当0＜y＜y01时，g(y)＞0，f′(x)＞0 ；当y01＜y＜y02时，g(y)＜0，f′(x)＜0；当y02＜y＜y03时，g(y)＞0，f′(x)＞0；当y＞y03时，g(y)＜0，f′(x)＜0

则f(x)的图像是“先严格单调增加再严格单调下降后严格单调增加最后再严格单调下降”，呈“M”形，f(x)具有“双峰”特征。

针对情形二与情形三，f(x)的图像可能是（1）“先严格单调增加后严格单调下降”，呈“倒浴盆”形；（2）“先严格单调增加再严格单调下降后严格单调增加最后再严格单调下降”，呈“M”形，具有“双峰”特征。针对情形四，f(x)的图像可能是（1）“先严格单调增加后严格单调下降”，呈“倒浴盆”形；（2）“先严格单调增加再严格单调下降后严格单调增加最后再严格单调下降”，呈“M”形，具有“双峰”特征；（3）“先严格单调增加后严格单调下降再严格单调增加再严格单调下降最后再严格单调下降”，具有“三峰”特征。值得注意的是，针对不同的参数考察其密度函数的图像，发现“三峰”现象并没有出现。

针对不同的参数取值，其密度函数f(x)的图像见图1至图4所示：

图1 α=1，β=1，m1=2，m2=3

图2 α=10，β=1，m1=2，m2=3

类似于定理1的证明，针对GBSI(m，α，β)、GBSII(m，α，β)分布分别得到如下定理2与定理3的结论。

定理2：设X～GBSI(m，α，β)，则（1）当0＜m≤1时，X的密度函数f(x)呈“倒浴盆”形；（2）当m＞1且时，f(x)呈“倒浴盆”形；（3）当m＞1且有可能呈“单峰”或“双峰”形。

图3 α=10，β=1，m1=4，m2=2

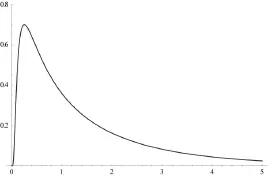
图4 α=1，β=1，m1=0.5，m2=0.4

定理3：设X～GBSII(m，α，β)，则当m＞0.5时，X的密度函数f(x)有可能呈“倒浴盆”形，也有可能呈“双峰”形；当m＜0.5时，f(x)有可能呈“倒浴盆”形，也有可能呈“双峰”形或“三峰”形。

值得注意的是，针对不同的参数考察其密度函数的图像，发现当0＜m＜0.5时，并没有“三峰”现象没有出现，而当0.5＜m＜1时，没有“双峰”现象出现。

3 结论

本文对Birnbaum-Saunders疲劳寿命分布进行了推广，提出了一种广义四参数Birnbaum-Saunders疲劳寿命分布GBS(m1，m2，α，β)，而两参数Birnbaum-Saunders疲劳寿命分布BS(α，β)、广义三参数Birnbaum-Saunders疲劳寿命分布GBSI(m，α，β)和GBSII(m，α，β)都是其取特定参数后的特殊情况。同时，研究了该分布的性质及密度函数的图像特征，其密度函数可能呈现“单峰”、“双峰”或“三峰”的形态，因此可以用它更好地拟合一些失效产品的寿命规律。