基于局部权重调节的自适应LOESS方法

何云飞，杨联强

（安徽大学 数学科学学院，合肥 230601）

0 引言

假定观测数据 (X1，Y1)，…(Xn，Yn)，i=1，2， ...，n是来自二元总体(X，Y)的一组简单随机样本，则X和Y之间的回归模型通常建立为Yi=m(Xi)+εi，i=1，2，…n。其中X是预测变量，Y是响应变量，m(x)称作回归函数。εi是随机误差，简单情况下，通常假定εi，i=1，...，n。独立同分布且E(εi|x=Xi)=0，则回归分析的任务是求出回归函数E(Y|X=x)=m(x)。

回归模型的求解通常可分为参数方法和非参数方法[1]。如果m(x)为特定形式的函数形式，只是其中参数未知，通常称为参数模型。经典的参数模型代表是线性模型，该方法有完善的理论和应用体系，被经济、社会等领域广泛使用。但参数模型的缺点是先验的设定了回归函数的形式，容易发生模型设定错误[2]。非参数模型是对参数模型必要的补充，其并不用假定回归函数的具体函数形式，而是用特定的方法将回归函数构造性的拟合出来[3]。经典的非参数回归的方法有很多,局部多项式回归[4]是其中一种具有代表性的方法，Cleveland（1979）[5]将该方法扩大到更一般的情况，Hastie和Tibshirani（1986）[6]对其更进一步扩展到多元模型。局部多项式回归在很多场合有着非常好的表现[7]，但局部多项式方法对于密集程度不均匀的数据（即非等间隔的数据）拟合效果却并不理想[8]。因此，改进局部多项式回归核函数中的带宽成为一个有价值的研究问题[8.9]。其中，LOESS方法最初由Cleveland(1979)提出，后由Cleveland和Devlin（1988）[10]加以完善，该方法通过数据在预测变量上分布的稠密性来自动调整局部权重，从而使得模型对非等间隔数据有更好的自适应性。

然而，LOESS方法只是考虑数据在预测变量方向上分布的不均匀性，却没有考虑数据在响应变量方向上波动特征的非齐性。本文通过基于观测数据局部波动特征的调节,构造了一种新的自适应LOESS方法，既保留了传统的LOESS方法相对于局部多项式方法在非均匀分布数据拟合时的优越性，又使得模型在拟合具有非齐性波动特征的数据时，有更良好的自适应性。模拟和实际应用的例子显示该方法将优于LOESS方法。

1 局部多项式回归与LOESS回归

首先对局部多项式回归以及在此基础上的LOESS方法作简介。

设 (X1，Y1)，(X2，Y2)，…(Xn，Yn)为来自 (X，Y)一组样本值，其回归函数形式为：

在局部多项等式m(Xi，x)中，当预测点Xi接近x时，在该点处的多项式则为：

式（1）是在x用Taylor公式展成p次多项式。其中局部多项式（1）中的系数{a0(x)，a1(x)，a2(x)，…，ap(x)}是使下式最小化所得到的：

其中使用高斯核函数：

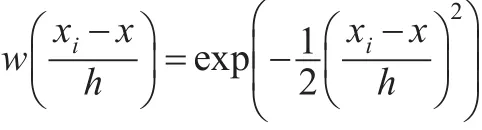
其中h是用来决定估计光滑度的正的常量，称为带宽。

为通过矩阵简化计算，设：

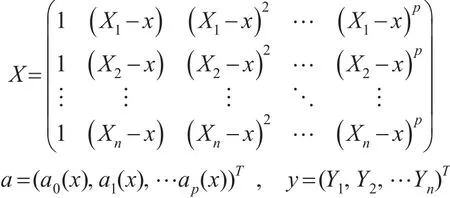
对角矩阵定义如下：

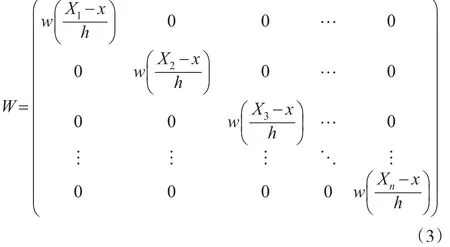
通过以上矩阵和向量可以将式（2）写成矩阵形式如下所示：

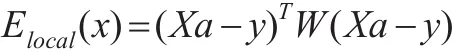
并最小化即可得到其系数估计值为：

以上是局部多项式回归，但是其缺点是对于处理非等间隔的数据时并不能达到一个很好的拟合效果。LOESS方法与局部多项式的区别在于通过带宽的局部化，从而使得拟合目标函数中权重局部化，即将式（2）改写为：

其中w是核函数，h是x和k的函数，hk(x)定义为离x第k个近的点Xi到其的距离。若取s∈(0，1),令k=[ns]，即取k是比ns大的最小整数，s被称为带宽调节因子。相应的，拟合的目标函数变为：

其中：

并最小化即可得到其系数估计值为：

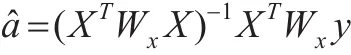
从局部权重的对角矩阵中可以看出LOESS对密集程度不一致的数据有更好的自适应性。

2 基于局部权重调节的自适应LOESS方法

由上文可见，相比较局部多项式回归中对角矩阵(3)中核函数的h固定不变，LOESS对角矩阵中的k近邻距离

hk(x)能够随着数据关于Xi的密集程度而改变，在Xi密集的位置，hk(x)取值较小，而在Xi稀疏的位置，hk(x)取值较大。但是，这种方法没有考虑观测数据在Yi维度上的波动特征。假设在所展开的x附近有离群点或者在纵向上有偏差较大的点时如果也按LOESS方法中距离越近其权重越大则容易导致较差的拟合效果。基于这点，在LOESS方法的基础上，本文考虑构造一个包含观测数据在因变量方向上变化特征的权重，使得在所展开的(xi，Y(i))附近的点无论是从解释变量方向上还是响应变量方向上，距离(xi，Y(i))越远其权重越小，越近则权重越大。其中Y(i)为距xi最近的响应变量，即当xi为实际观测值时，Y(i)为xi对应的因变量；当xi为其取值范围内的非观测点时，Y(i)

则为距xi最近的因变量观察值对应的响应变量观测值。权重的构造形式是在LOESS方法上作如下改进:

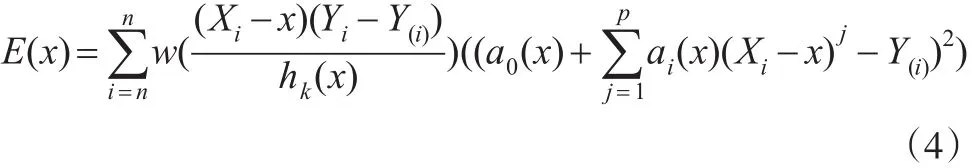
要估计系数，最小化上式，其方法与步骤与LOESS方法一样。可解得为：

其中：

在实际情况中，对于一固定点(x，Y(i))，其附近的点到其距离越近受其影响则越大（相关性越强),即无论在自变量方向上还是因变量方向上，到该点距离远的受到该点的影响较小，对应的权重就小，反之，距离近的权重就大。

3 模拟

下面将通过三个实例来显示改进后的自适应LOESS的拟合效果。并比较两种方法在相同的带宽下留一交叉验证得分(CV)值和估计的均方误差(MSE)的大小。

例 1：（Doppler）函数表达式f(x)=5(x(1-x))0.5sin(2π(1+c)/(x+c))，c=0.05，yi=f(xi)+εi，xi∈[0，1]，等间隔取值，εi～N(0，0.22)。取样本容量为n=200的数据集并分别应用传统的和改进后的LOESS方法进行估计，结果如图1至图3所示。其中，图1分别是真实函数图像和两种方法所估计的函数图像，其中两种方法估计的函数图像都是在最小的CV值下的图像，此时两者的差异并不明显,但计算可得此时两种方法的CV分别为0.43368和0.19837，MSE分别为6.7317和4.8673。图2是在s=0.2时两者的估计图像，此时可明显地看出改进后的方法较传统的LOESS方法有更好的拟合效果。图3是CV值和MSE关于s的函数图形，可以看出在相同带宽下改进后的自适应LOESS的CV值和MSE均小于传统的LOESS方法。

图1 Doppler函数及其估计值图像

图2相同带宽下的估计图像

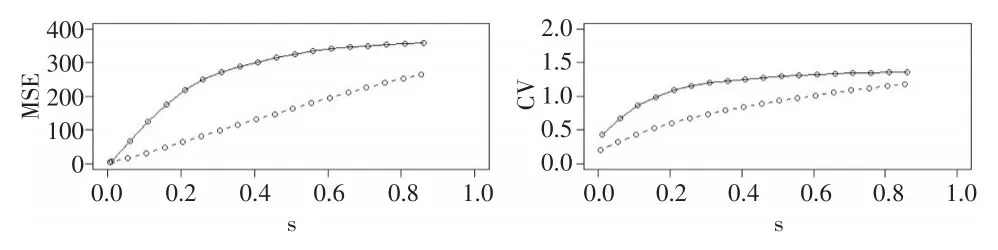
图3MSE和CV关于带宽参数s的变化图像

例2：（Mexican Hat）该函数表达式为f(x)=-1+1.5x+0.2φ(x-0.6)，其中φ表示标准正态分布的密度函数，，其中样本容量为n=200。分别应用传统和改进之后的LOESS进行估计，结果如图4至图6所示。图4分别是真实函数图像和两种方法所估计的函数图像，其中估计的函数图像都是在两种方法最小的CV值下的图像，可看出改进后的LOESS方法的估计效果更好。计算出此时两种方法所对应的是CV值分别是0.41076和0.193745，MSE分别为26.1369和0.8363。图5是在s=0.15时两者的估计图像，此时两者的估计效果均差于在各自最小的CV值下的图像，但改进后LOESS方法依旧优于传统LOESS方法。图6可看出，在相同带宽下改进后的自适应LOESS所求出的CV值和MSE均小于传统的LOESS方法。

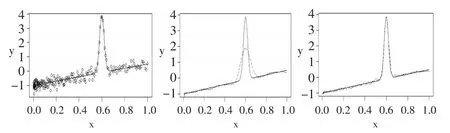
图4 Mexican Hat函数及其估计图像

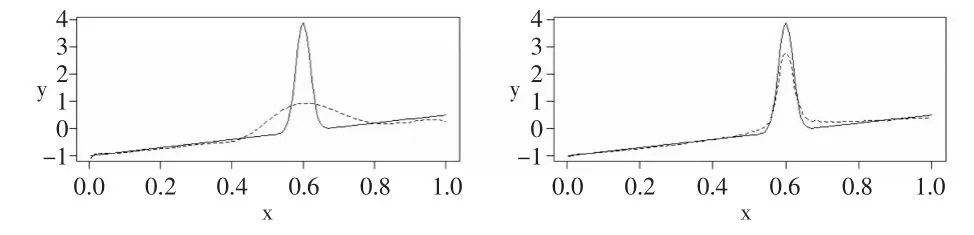
图5相同带宽下的估计图像

图6MSE和CV关于带宽参数s的变化图像

例3：设f(x)=sin(0.1πx)+0.7sin(1.23πx)+0.5cos(2.7πx)+0.2sin(0.6πx)，其中样本形式为yi=f(xi)+εi,xi∈(0.2，0.3，…，19.9，20，20.5，…39.5，40)，εi～N(0，0.22)，样本容量为238。分别应用传统和改进后的LOESS方法进行估计，结果如图7至图9所示。图7分别是真实函数图像和两种方法所估计的函数图像，其中两种方法估计的函数图像都是在最小的CV值下的图像，此时改进后的方法在处理这样波动性较大且密集程度不一的数据时的能力明显好于传统LOESS，计算此时两者的CV值分别为0.50736和0.21673，MSE分别为0.1982和0.1932。图8是在各自最小的CV值下的图像，改进后的自适应LOESS方法依旧优于传统LOESS方法。图9可看出，在相同带宽下改进后的自适应LOESS所求出的CV值和MSE均小于传统的LOESS方法。

图7模拟函数及其估计图像

图8相同带宽下的估计图像

图9MSE和CV关于带宽参数s的变化图像

4 应用

本文将用传统LOESS和改进后的自适应LOESS方法对2015年我国的A股收盘指数进行估计，数据来源于Wind(万得数据库)。

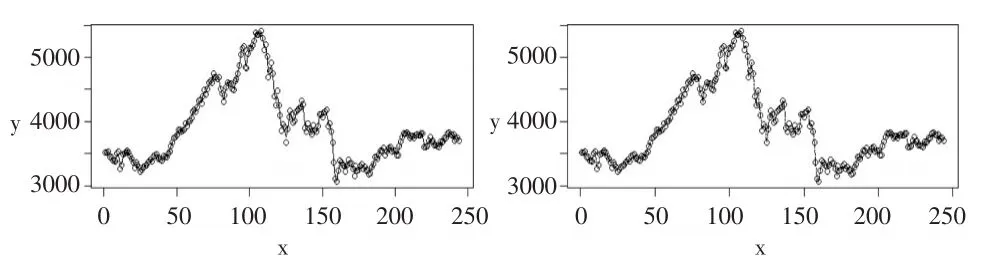
图10在s所能取到的最小值时的拟合图像

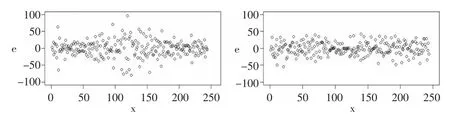
图11残差图

图10并不能明显观测出两种方法的估计的差异，然而从图11可以看出传统LOESS方法的残差的波动性方面差于改进后的LOESS。传统LOESSS方法的残差不仅总体上比自适应LOESS方法大，而且出现了显著的异方差性，而自适应LOESS方法的残差则平稳很多。说明自适应LOESS方法在处理观测数据局部波动特征非齐性时较传统LOESS方法具有更强的自适应性。

5 总结

本文针对局部多项式拟合的思想，通过构造包含因变量方向上变化特征的权重并加入LOESS模型，使得模型在估计因变量波动特征具有局部非齐性时具有更强的自适应性。相比于传统LOESS方法，新方法并没有显著提升模型复杂度，却提高了对这些复杂数据的拟合精确性。模拟和实际应用显示新方法明显提升了对复杂数据的拟合和趋势滤波能力。当然，对该方法估计结果的渐进性质分析是待完成的重要理论研究工作。