一类改进的贝叶斯模型选择方法

井晓丹，朱永忠，井 睿

（1.河海大学 理学院，南京 211100；2.西北农林科技大学 经济管理学院，陕西 咸阳 712100）

0 引言

模型选择是建模的基本问题之一，对模型进行选择的目的是选择输入变量的一个最小子集，并使最终模型具有较好的预测性能。在最优模型选择过程中，要充分考虑计算的复杂程度和模型的预测性能。

到目前为止，许多科研工作者对贝叶斯模型选择进行了大量的研究，得出了很多模型选择方法[1]。在模型选择时，常用的方法是根据预测性能对模型进行选择。交叉验证法[2]和广义信息准则[3]都可以得到模型预测性能的一个渐近无偏估计[4]，但不是真正无偏估计模型的泛化能力。当给定的数据集较小时，这两个估计中含有随机误差项，较大的方差可能会导致过拟合现象，在模型选择过程中导致选择非最优模型以及在所选模型的性能估计中产生偏倚[5-7]。模型选择的另一种方法是构建一个完整的参考模型[8-10]，这种方法给出的预测模型几乎与参考模型一致。如果完整的模型过于复杂或观察所有变量的成本太高，那么该模型可以通过投影方法稳健地简化，将全模型的信息投影到子模型上。投影方法考虑到形成全模型时模型的不确定性[11]，将参考模型的后验信息投影到候选模型，从而使候选模型中的方差减小,降低模型中的过拟合现象。在预测性能方面，投影方法似乎优于其他的模型选择方法，但对于不同大小的数据集，投影方法对模型中自变量数目的选择[12]存在不确定性。鉴于此，本文在对模型进行选择时将k折交叉验证与投影预测法相结合，数值实验结果表明，改进后的方法能选出具有良好预测性能的最简模型。

1 常用模型选择方法

1.1 预测性能

统计学家们通常用效用函数描述模型的质量，一种常用的衡量候选模型M预测性能好坏的效用函数[13]是：

其中，y͂表示未来预测值，表示训练数据集。

由于未来预测值是未知的，导致效用函数u(M，͂)无法求值。因此通常将式（1）的计算用下式代替：

（1）留一交叉验证

式（2）可以通过使用已获得的数据集D代替真实数据进行计算，生成概率分布pt(͂)的一个估计。但使用与拟合模型相同的数据集D，会导致泛化能力有一个乐观的估计。为了解决这一问题，1974年Geisser[14]等提出留一交叉验证法，即将给定的数据集分成两部分，一部分作为训练集，用于拟合模型；另一部分作为测试集，用于检测模型的预测性能。其基本思想是：每次从数据集D=

中取一个样本(xi，yi)作为测试集，用剩下的n-1 个 样 本(xn，yn)}组成训练集。将此步骤重复n次，依次取遍所有的n个样本分别作为测试集，最后用n个测试误差的均值作为泛化误差的估计。

由于模型需要被拟合n次，导致留一交叉验证法的计算量可能很大。如果n很大，不仅拟合次数很多，也会使得拟合单个模型的过程变得特别慢，那么，这种方法将非常耗时。

(2)k折交叉验证

1979年，Geisser和Eddy[2]提出了k折交叉验证。k折交叉验证是一种常用的样本重用方法，它与留一交叉验证

其中，pt(͂)是概率分布，下标t代表此概率分布是由真实数据计算得到的。这个表达式粗略地描述了候选模型M的预测性能。

1.2 交叉验证

法类似，其本质区别在于数据的切分方式不同。

k折交叉验证的基本思想是：将数据集等分成k个子集I1，…，Ik，每次从中取一个数据集作为测试集，而其余k-1个数据集作为训练集，重复此步骤k次。平均k次的结果作为泛化误差的估计：

其中，Is(i)表示将第i个样本集作为测试集，DIs(i)表示在训练集中将第i个样本集删除。

k折交叉验证中，较小的k会使方差变大，导致模型预测效果变差。统计学家们通过利用大量数据集，使用不同方法进行大量的实验，表明10折是获得最好误差估计的恰当选择。但这也不是绝对的，争议仍然存在。令k=10其优势在于：第一，方便计算。使用10折交叉验证只需要把模型拟合十次，可行性更高；第二，考虑到偏差-方差的权衡问题，令k=10时，会产生一个中等程度的偏差，使得测试误差的估计不会有过大的偏差或方差[15]。本文中将使用k=10进行讨论。

1.3 广义信息准则

广义信息准则可以估计模型的预测性能，包括参数的不确定性，也可以用于异常模型。其估计模型泛化能力的公式为：

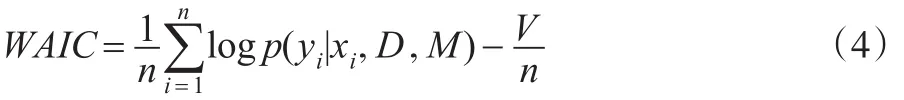
其中，V是函数方差，由下式给出：

其中，·||·是布尔运算中的“或”运算，θ是模型参数。

参考模型M*和候选模型M之间的差异定义如下：

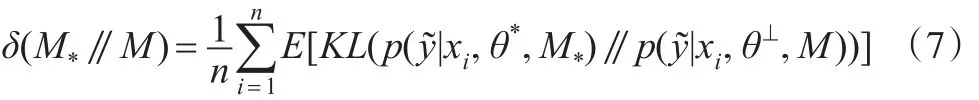
这里，两个期望都采用了后验概率p(θ|D，M)。

1.4 投影预测方法

模型选择的另一种方法是建立一个参考模型M*，这种方法称为参考模型法[8-10]。从预测角度看，用所有的变量形成参考模型将会得到更好的预测效果。参考模型法被认为是对未来预测值的最好拟合。投影预测方法是参考模型方法的一种表现形式。

投影预测方法的基本思想是：将参考模型M*的后验信息投影到候选模型M上，因此候选模型的预测分布与参考模型的分布非常接近。候选模型的参数是由拟合的参考模型决定的，而不是由数据决定。

给出参考模型的参数θ*，在候选模型M的参数空间上，投影参数θ⊥定义如下：

计算KL散度，并根据式（6）分别计算出投影参数那么式（7）近似等于：

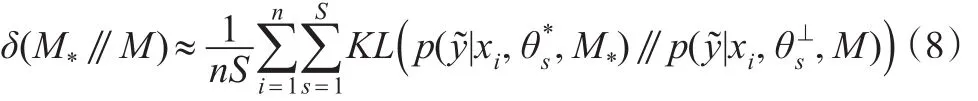
Dupuis和Robert[16]提出了模型选择的一种方法:

其中，M0代表空模型，它与参考模型的差异是最大的，从变量选择角度看,M0是自由变量模型，M*代表参考模型，M代表候选模型。Dupuis和Robert指出，在模型选择过程中，要选择具有较好解释能力的最简模型，但他们没有讨论模型预测性能这一阈值的影响。一般情况下，对子模型的预测性能来说，ϕ(M)是一个不可靠的指标。这是因为通常情况下，参考模型M*与真实数据生成的模型Mt是不同的，且M和M*之间存在差异，但M，M*却与Mt有相同的预测性能。

投影方法考虑到形成全模型时的不确定性，能最好地保留全模型的预测性能。但在一般情况下，参考模型和子模型之间预测性能的差异是一个不可靠的指标。这个属性使得投影方法不容易确定最终模型的大小。

1.5 模型空间方法

在模型空间上有如下分布：

其预测通过贝叶斯模型平均(BMA)获得:

严格来说，BMA假设候选模型是真实数据生成的模型。此外，在变量选择的背景下,BMA已被Raftery[17]证明在理论上和实践中都具有良好的预测性能。

2 一类改进的贝叶斯模型选择方法

2.1 模型改进

投影方法的预测效果虽然很好，但它决定最终模型中自变量数目的效果并不理想。针对这一点，本文在对模型进行选择时将k折交叉验证与投影预测法相结合对其进行改进。

其基本思想为：使用投影方法进行变量搜索，将显著性变量作为训练集；交叉验证时，训练集用来确定模型的大小，测试集对最终选择的模型在独立数据集上的性能进行预测。

选择中的过拟合现象和选择的偏倚取决于模型预测性能估计中的方差和用于比较的候选模型数量。对于后者，与在变量组合中用逐步回归法选择模型相比，改进后的方法中，交叉验证法通过比较p+1个模型（变量已经排序），降低了模型的比较数，当仅用来决定模型大小时，它产生的过拟合是相当小的。

对模型中自变量进行选择时，应尽可能地使自变量个数达到最少，而且模型具有较高的预测精度。改进后的方法允许在模型的预测性能和模型中自变量个数之间进行取舍，在损失较少预测精度的基础上简化模型。

对于临界值U和α，变量选择时应满足的条件为：

其中，ΔMLPD(m)表示交叉验证时训练集中m变量的样本外预测，U表示为了减少模型中自变量数量而损失的预测精度，α是置信水平。

方法改进后，k折交叉验证令搜索重复进行k次，然后对预测模型进行拟合，需要注意的是：在这个过程中参考模型也被拟合了k次，每次也是用相同测试集中的数据对模型的预测性能进行估计。因此可以比较预测模型和参考模型在独立数据集上的预测性能，并进行估计，进而判断选择的模型是否是最优模型。

改进后的方法优点在于：第一，降低了模型的复杂程度，能够保证模型中所含自变量的准确性；第二，考虑到形成全模型时的不确定性，能够最好地保留全模型的预测性能，准确给出模型预测性能的一个渐近无偏估计。

2.2 数据仿真

2.2.1 模型

下文将讨论线性模型中的回归问题。对于回归，这里采用标准的高斯模型：

其中，x是输入变量的p维向量，ω是对应的权重，σ2是噪声的方差。因为超参数τ2是共轭先验的，因此这个模型在大部分情况下都可以求解。对于回归模型（13），通过在输入向量x=(x0，x1，…，xp)和相应的权向量ω=(ω0，ω1，…，ωp)中增加常数项，将截距项计入。参数ατ，βτ，ασ，βσ的值将在数据集的描述中一起给出。

由于考虑变量的选择问题，因此子模型中输入变量的数目不同，使得x和ω的维数是变化的。在预测性能的比较中，参考模型M*使用BMA[16]。

2.2.2 数据仿真

本文将进行两个仿真实验，分别采用不同评价指标比较 LOO-CV、CV-10、WAIC、BMA-Proj、IMP-Method的预测性能和变量选择，并由此说明方法改进后的优越性。为了在模型选择方法之间产生有效的比较，在每次实验中，各种模型选择方法都在相同的训练集和测试集对上进行。

首先，做一个模拟的变量选择实验，用以说明不同方法之间的差异。数据分布如下：

仿真实验中，将变量总数设为p=100。对所有变量进行分组，每组五个变量。每个变量xj的均值为0，方差为1，且与同一组中其他变量相关，相关系数设为ρ，但与其他组的变量均不相关。将前三组变量的权重设为（ω1∶5，ω6∶10，ω11∶15） =（ξ，0.5ξ，0.25ξ），其余变量的权重设为0。常量ξ调整数据集的信噪比。也就是说，在数据集中有15个相关变量，85个无关变量。将训练集的大小设为n=100，300，500，令相关系数ρ=0，0.5，0.9，为了得到不同水平相关系数ρ的比较结果，将ξ的值设为σ2Var[y]。在回归模型(13)中，令参数ασ=0.5，使用BMA作为参考模型M[18]。*

对每个 (n，ρ)的组合，模型选择方法见表1。LOO-CV、CV-10、WAIC、BMA-Proj中用逐步回归法对变量进行搜索，即从空模型开始，使每一步选入的变量都最大限度地增加了模型的预测性能。

表1 数据仿真中使用的模型选择方法

将预测模型在数据量为n͂=1000且与训练集数据不相关的测试集上进行测试。对模型的预测性能进行评价时，使用对数预测密度的均值(MLPD)：

为了更直观地比较不同方法的预测性能，用下式表示性能差异：

其中，M是选择的子模型，M*是参考模型(BMA)。若ΔMLPD(M)=0，则说明所用方法与BMA有相同的预测性能；出现负值说明所用方法的预测性能比BMA糟糕；相对应的，正值表示所用方法的预测性能更好。由于BMA已经被证明具有良好的预测性能[11，17，19]，因此对模型进行选择的目的是希望找到与BMA预测性能接近的最简模型。

图1模型选择方法的比较

图1左列中正方形、圆形以及三角形对应的横坐标表示模型中自变量的平均数，灰色线表示数据集中相关变量的数目是15、右列中正方形、圆形以及三角形对应的横坐标表示不同模型选择方法的预测性能与BMA预测性能的差异大小，三条垂直的点线代表空模型的性能（仅指截距项），正方形、圆形以及三角形代表变量间相关水平的强弱（相关程度见图例）。

从图1可以看出：仿真实验中使用的所有方法的预测性能都不如BMA方法的预测性能好。从预测的角度来看，模型平均通常会产生最好的预测效果。因此，对模型进行选择的主要目的是简化模型，并且基本上不会影响预测的准确性，而不是试图通过考虑模型的不确定性来提高预测精度。

其次，对于小数据集（n=100）的模型选择，LOO-CV、CV-10、WAIC选出的模型预测性能比较差，甚至比没有变量的模型（右列中三条垂直的点线）预测性能更糟。这是因为缺乏数据，预测性能估计中的高方差导致选择了过拟合的模型。过度拟合是一个潜在的问题，阻碍模型的选择，尤其是当数据集较小时，会导致估计中的高方差，高方差对模型预测精度的提高是不利的。此外，从图1可以看出：变量间的高相关性在一定程度上改善了预测效果。上述三种方法仅对大数据集（n=500）的预测性能较好。相比之下，投影预测法的预测效果明显更好，特别是对于小的数据集（n=100），其预测性能接近BMA。但从左列可以看出：在不同大小的数据集上，投影方法选择的模型中自变量个数的变化比较大，在小数据集上模型复杂程度较大。而方法改进后，模型中自变量个数趋于稳定，在较小数据集上模型的复杂程度变小，且模型的预测性能仍接近BMA的预测性能。

采用逐步回归法对变量进行排序，然后重新进行实验，并将模型的CV效用和测试效用作为评价模型性能的指标。

图2 CV效用和测试效用

图2中虚曲线表示CV效用，代表模型选择中的过拟合现象；实曲线表示变量排序后的测试效用。两条曲线之间的距离表示选择引起的偏倚。垂直虚线表示模型中自变量的平均数。

令ρ=0.5，用逐步回归法对变量进行选择。CV效用（10折）用选出的显著性变量进行计算，测试效用在数据集中余下的其他数据上进行计算。

由图2可知，前三种方法中，所选模型预测性能的变化是非常大的。在不同大小的数据集上进行变量选择时，模型选择中出现过拟合现象，而且当训练集变大时，选择过程中的过拟合现象减小；从空模型开始，在预测模型中一次添加一个变量，模型的CV效用比较高，但测试效用却很糟糕。也就是说，用逐步回归法对变量进行选择时，模型的预测性能被高估。由此可知，经过变量选择后，CV效用是一个乐观的估计。但是对空模型和包含所有变量的模型而言，CV效用和测试效用几乎相同，因为这些模型不涉及任何选择。

与LOO-CV、CV-10、WAIC相比，投影预测方法中测试效用的变化程度小，且不容易产生过拟合现象。但从图2可以看出：投影方法对模型中自变量个数的选取并不理想。

方法改进后，模型的复杂程度降低，且仍具有良好的预测性能。当增加多个变量时，子模型会越来越接近参考模型(BMA)，从而避免了预测精度下降的问题。

表2 改进前后模型中自变量个数及CV值的比较

由表2可知，方法改进后模型的大小趋于稳定，但预测精度略有下降；样本量越大的数据集确定的模型越合适。

通过数据仿真可以看出：改进后的方法产生了较好的预测效果，它简化了模型，而且不会失去太多的预测精度。在寻找预测性能良好的最简模型时似乎是最稳健的方法。

3 总结

本文将k折交叉验证与投影预测法相结合对模型进行选择，通过仿真实验说明了使用这种方法对模型进行选择时，能选出具有良好预测性能的最简模型。但改进后的方法也存在一些问题，方法改进后不仅增加了计算量，而且预测精度略有下降。针对出现的不足，还需要进行更深入的研究。