相关性失效下二终端网络系统可靠性评估模型

邓 川，唐家银，谭启涛

（西南交通大学 数学学院，成都 611756）

0 引言

科技进步和交互型模式的发展使得网络系统扮演着越来越重要的角色。供电网络、交通网络、计算机信息网络等网络系统的失效会引起很大的社会经济损失，甚至造成安全事故。所以网络系统可靠性的评估是值得关注的研究领域。网络系统可靠性研究方法以概率真值表法、全概率分解法、最小路集法等为代表；且多数基于最小路集研究网络系统可靠性，在组成系统的单元部件独立性失效条件下，国内外学者已经做了大量的研究，这些研究主要集中在求最小路和不交化上，且相关理论研究[1-9]较为成熟。

邻接矩阵法求最小路是一种常用的方法[2]，它依靠简单的矩阵幂运算求得二终端网络系统的所有最小路。但是网络中弧的数量较大时，矩阵的幂运算是非常繁琐的，特别是遇到复杂的大型网络，邻接矩阵法就不再适合求最小路了。文献[3]给出了余因子算法(一种基于行列式求最小路的方法)。它在邻接矩阵的基础上做了降阶，并且将幂运算转变为行列式运算，使得计算简化。

使用余因子算法[3]和改进BDD算法[4]可简便地得到不交和事件，在各部件独立失效下，可以通过简单的计算求系统的可靠性。因为通过余因子算法求出的最小路之间一般是相交的，所以为了方便计算系统可靠度，还需要进行不交化。对不交化技术的大多数研究都是基于容斥原理。Sing等[5]研究了终端网络可靠性问题，肯定了使用二元决策图来确定终端网络可靠性的合理性。Yeh[6]对求不交化的和的技术进行了改进，得到了最小的路径结构(MPS:Minimal Paths Structure)。基于一个有序二元决策图(OBDD:Ordered Binary Decision Diagram)，Kuo等[7]为大型网络的可靠性评估建模奠定了基础。并且在文献[8]中将二终端的情况推广到了k终端。史玉芳等[4]改进了BDD算法，并给出了编程的步骤与算法案例。

实际工况中，由于相同的工作环境和外部冲击，导致系统各组成部件失效之间相互影响。独立性仅是相关性的一个特例，忽略相关性失效可能会对模型的精确性造成影响。考虑相关性失效下二终端网络系统问题可靠性建模具有一定必要性，Copula相关性理论是刻画统计相关性的重要工具[10-12]。

本文借助余因子算法和BDD算法，引入Copula的相关性理论和差分运算，对二终端网络系统进行可靠性评估，使得进行网络系统可靠性计算时能有效克服维数灾难。

1 二终端网络系统的最小路

求解二终端网络系统问题的可靠度，对于理论研究和工程推广应用都有价值。如何计算系统正常的最小路，是研究系统可靠度的基础。曹晋华等[2]给出了求最小路的邻接矩阵法。在网络系统中弧的数量较少时，此方法能方便地给出最小路的集合，它所用到的知识也是较完备的矩阵理论，即邻接矩阵的幂运算。当系统弧的数量较多时，矩阵维数相应增大，矩阵乘法的难度呈指数化增长。即使使用计算机运算，由于算法的繁琐，也会影响计算速度。引入一种余因子算法，将计算简化为矩阵行列式的运算。

网络系统G是有n个节点l条弧的二终端网络系统。C是G的邻接矩阵，I是与C维数相同的单位矩阵，则G的广义邻接矩阵为C+I，（即每个节点增加一个权为1的自环[3]）。

假设输入节点为i，输出节点为j。余因子算法步骤如下：

（1）根据网络系统G写出对应的广义邻接矩阵C+I；

（2）删除矩阵C+I的第j行和第i列，得到余因子矩阵Mji；

（3）计算Mji对应的行列式值，记为|Mji|；

（4）|Mji|是一些弧序列的和，需要先对这些序列做类似于邻接矩阵法里的去除冗余项处理，然后取纯真值，得到的每一个弧序列就是一条最小路。

如文献[2]中桥形网络的广义邻接矩阵与余因子矩阵为：

基于上面的步骤，将最小路记为Ai(i=1，2，…m),令中事件的并记为S，即系统正常这一事件。

余因子算法的合理性、适应性(对任何无向、有向和混合网络都适合)在文献[3]中给出了具体的证明。在二终端的网络系统问题中，对比邻接矩阵法求最小路集，余因子法有利于编程实现，并能提高运算效率，具有易操作的特点。

2 基于改进的二元决策图法化S为不交和

从桥形网络的案例可以得到Ai(i=1，2，…m)之间并不是互斥事件，根据网络的特点也不难发现A中事件一般不是互不相容的。为了方便计算系统G的可靠性，需要将事件Ai(i=1，2，…m)进行不交化。改进的二元决策图算法[4](后文都简记为BDD算法)可以方便快捷地得到不交和。

系统可靠度R为：

直接求可靠度R是有困难的，将A中元素不交化有利于简化计算，下面就将A中事件化为不交和。

记f为系统的布尔函数，，如桥形网络：f=ab+cd+ade+bce，其中f是关于弧a，b，c，d，e的函数。对于n个节点l条弧的二终端网络系统，布尔函数为：f(x1，x2，…，xl)。将布尔函数进行0-1分解有：

其中i∈(1，2，…，l)。

如果E(xi)表示f中包含弧xi的弧序列的集合，令L(xi)为E(xi)中最短弧序列中弧的数量。如桥形网络中，E(a)为{ab，ade}，L(a)=2。由BDD算法[4]，化不交和的算法步骤可以简记如下：

（1）计算f中每个弧xi的L(xi)，取最小的L(xi)对应的xi，对此弧进行布尔代数的0-1分解，并用二叉树表示。二叉树的左枝为1，弧xi正常；右枝为0，弧xi失效。如果最小的L(xi)有多个，则在这些相等的里面取在f中出现最多的xi进行；其余情况任取。

（2）更新布尔函数f：当xi取1(或0)时，f中对应的xi取1（或0）。将f中xi取1的布尔函数赋给左叶节点，将f中xi取0的布尔函数赋给右叶节点。

（3）重复步骤（1）、（2），直到所有叶节点对应的布尔函数出现1这一项或布尔函数等于0。1表示此叶节点到根节点是一条不交化的最小路，0表示此叶节点到根节点不是最小路。

经过上述不交化处理，可以容易得到不交化的最小路集。将之记为B1，B2，…，Bh，其中h为叶节点中取1的个数。网络系统G的可靠性可以表示为在不交化的过程中，该算法可以进一步简化为只对那些弧数量小于n-1的最小路不交化，其他最小路只需要添上未出现弧的失效状态。

3 相关性失效下二终端网络系统G的可靠度计算

对B1，B2，…，Bh的研究，国内外都是基于弧与弧失效之间相互独立，将弧序列Bj中的弧xi用Ri替换，xˉi用1-Ri替换，就可以得到网络的可靠性。由于受到相同的冲击以及处在同样的工作环境中，使独立情形下的可靠度计算结果存在偏差，从而考虑网络G的组成弧之间的相关性是非常有必要的。因此，引入Copula函数的相关理论，解决相关性失效下的二终端网络系统系统可靠性的问题。Copula理论预备知识如下：

定义1[15]：n维Copula是一个函数C：[0，1]n→[0，1]，而且满足：

（1）∀u∈[0，1]n，C(u)=0，如果u至少存在在一个分量为0；C(u)=uk，如果除uk外，其余分量全为1；

（2）对任一属于[0，1]n的a，b，使得a≤b(对应的坐标分量ak≤bk)，有：VC([a，b])≥0。

Sklar定理[15]：令H是n维随机变量 (X1，X2，…，Xn)的联合分布函数，其边缘分布分别为F1，F2，…，Fn，则存在唯一一个n维Copula函数Cθ(u1，u2，…，un)，使得对所有Rˉn中定义域上的点(x1，x2，…，xn)有下式成立：

基于不交化的最小路集，得到网络G的可靠性为：现在将求二终端网络系统G的可靠性分解为求Bi的可靠性P(Bi)。不妨设弧xi的寿命为Ti，事件Bi中正常弧的数量有k条，失效有q条，未出现有l-k-q条。由概率论的知识有：

其中A表示事件{Ti1≤t}，…，{Tik≤t}的并。将事件记为B。

在不同的事件Bi中，下标k和q取不同的值。下标i1，…，ik是与事件Bi中正常的k条弧一一对应的一个排列。失效时的下标类似可得。则由加法公式[16]和式（4）有：

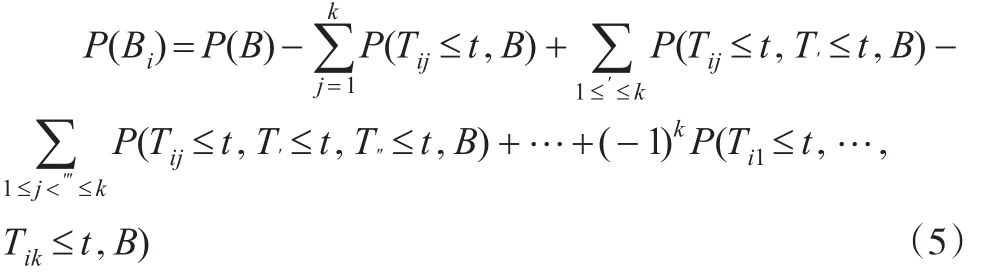
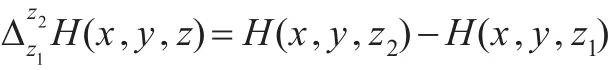
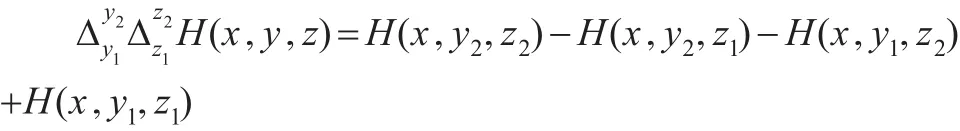
其他阶差分算子以此类推。

令H(x)为网络G所有l条弧的联合分布函数，则由Sklar定理存在一个l维的Copula函数为C(u1，u2，…，ul)，ui(i=1，…l)为弧xi的分布函数Fi(xi)，使得：

当k=1时容易得到：

当k=2时不难得到：

根据归纳假设不难证明事件的概率为：

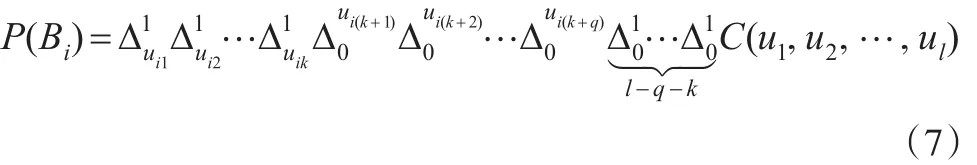
节点不可靠的时候考虑网络的相关性，只需要将节点视为弧，并进行相同的可靠度建模。此时Copula函数的维数会增加n维，但是这并没有给计算增加多少难度。对于任何一个Bi，只需要在节点可靠的基础上，对连接弧的节点做相应的差分运算，其中F(t)是节点的分布函数，要取遍所有在Bi中出现的节点。对没有出现的节点和弧做差分运算，实际运算过程中，由Copula函数的性质不难发现，这些弧与节点对应的变量都取1就可以了，其余差分按定义计算结果易得。

4 Copula函数的统计选择

在变量相关的情况下求联合分布函数是很困难的，但变量相关结构Copula拟合的统计捕捉相对较易。由Copula的优良性质知式（7）是容易计算的。而Copula函数C(u1，u2，…，ul)的选择需根据实际的网络系统弧寿命数据样本拟合得到。一般需要拟合出各弧寿命边缘分布函数Fi(xi)，根据(ui，uj)的散点图可以初步判断两变量相关结构剖面，依据剖面特征寻找出一族备选Copula。记备选Copula函数族为C0={C1，C2，…，Cq}。

利用已知的样本数据和极大似然估计，可给出每个备选函数中参数向量θ0的估计。对备选函数可以计算Jeffreys’离散测度[17]，求得最优模型。但是该方法对相关系数较大的案例并不适合。由文献[18]知，可以利用Bootstrap技术对备选函数抽样得到“原始数据”，然后从中重复抽取，每次都可以得到一个似然函数值，最后根据这些数据构造拟合优度检验统计量，寻找最佳的Copula函数。

常见的Copula函数族：如表1所示：

表1 几类典型Copula函数族

Copula函数的统计选择算法如下：

（1）根据部件间关系的初步分析，确定一族备选Copula函数{C1，C2，…，Cq}。

（2）对每个备选Copula函数Cj，j=1，…，q，将样本数据带入似然函数，利用极大似然估计求得参数θ̂j。

（3）从备选函数中选择两个进行似然比检验，根据统计量的值和显著性水平排除一个。

（4）从剩下的备选函数中选一个与上次检验剩下的函数再进行似然比检验。

（5）重复步骤（4）直到找到最优的Copula函数。

5 仿真案例

有如图1所示的星形网络系统G，假设每个节点是可靠的，每条弧是服从威布尔分布，并有单向弧的失效率函数是r(t)=9.8×10-5t，双向弧的失效率是r(t)=(7.7175×10-7t)1/2，其中时间单位是月。如果系统服从θ为1/2的Gumbel Copula。考虑系统工作到10年后，从节点1到节点2，系统正常的可靠度。

图1星形网络

由余因子算法得到邻接矩阵C和余因子矩阵C′：

去除冗余项之后得到的纯真值为：

经过步骤二BDD算法，容易得到不交化的弧序列：

上述弧序列已经不交，将其简记为B1，…，B15，通过Copula可以简单计算出15个弧序列对应的可靠度，一个简单的求和可以得出系统的可靠度。经过软件R编程计算得到独立时，系统的可靠度为R′=0.7424816，而考虑相关性失效，系统的可靠度为R=0.6591567。通过R绘图可以得到图2、图3所示的结果：

图2系统可靠度函数曲线

图3两种状态下的可靠度偏差

由图2和图3可以地看出大约在30个月之后，独立失效和相关性失效的可靠度曲线之间的偏差越来越大。而且相关性失效的可靠度比独立失效要小。出现这种结果是由于系统结构和部件相关性所导致的。如计算弧序列的可靠度，独立失效下的可靠度为(1-R1)R6R7，其中R1表示弧x1在此时此刻的可靠度；而在部件相关性干涉影响下，由于部件有正相关性(Gumbel Copula属于正相关性)作用，所以弧x6在弧x1失效的状态下可靠性是低于独立时的可靠度。由于这种相关性干涉的影响，使得不考虑相关性失效会造成对可靠性的高估，而这在工程里是非常危险的。这些失误往往是以巨额经济利益和生命安全为代价。

对于节点不可靠的情况，可以按照上面提到的方法进行推算，其结果是相似的。

6 结论

基于余因子算法和改进的BDD算法，求得不交的弧序列。借助Copula函数和差分理论，本文建立了相关性失效下二终端网络系统的可靠度评估模型。对于节点可靠的情况，已经做了详细论述，而对于节点不可靠的情况，本文找出了两种情况的共性，利用已有研究结果，给出了节点不可靠的计算方法。描述了Copula函数的选择方法与思想，为模型的建立提供了支持。

根据建立的可靠度评估模型以及仿真案例分析，得出在正相关性失效时，独立性条件下系统可靠度评估值偏大。经过对两种状态偏差的仿真算例分析，发现随着时间的增大，偏差在尾部趋向于线性增长。进一步可以得到在部件呈负相关时，忽略相关性，系统可靠度会偏小。

当面对大型复杂网络时，基于Copula函数考虑网络相关性仍然是有效的，本文给出的二终端网络系统可靠性评估模型，可以推广至k终端情形。但由于备选函数自身的局限性，使用Copula函数刻画部件的相关性仍然存在一些不足。