直线与抛物线位置问题变式探究

■江苏省沭阳高级中学 项敬磊

直线与抛物线的位置关系问题,看似简单,却变化万千。让我们从一个简单的例题谈起。

引例:过定点P(0,2)作直线l,使直线l与抛物线y2=4x有且只有一个公共点,这样的直线l共有____条。

分析:利用数形结合便可找到答案。

解:如图1,过点P与抛物线y2=4x仅有一个公共点的直线有3条:2条切线、1条与x轴平行的直线。

故答案为3。

评注:直线与抛物线只有一个公共点时,要考虑相交于一点的情况,不要漏掉。

变式1:直线l:y=x-1与抛物线y2=4x是否相交?如果相交,试求两交点之间的距离。

分析:可联立直线方程与抛物线方程,消去y后得到一个关于x的一元二次方程,通过考查判别式Δ的正负来判断它们的位置关系。而对于本题,由于直线l:y=x-1过抛物线y2=4x的焦点(1,0),故直线l与抛物线必相交。

解:因为直线l:y=x-1过抛物线y2=4x的焦点F(1,0),所以直线l与抛物线必相交。

设交点为A(x1,y1),B(x2,y2)。

图1

设A、B两点到准线的距离为|A A′|、|B B′|,则:

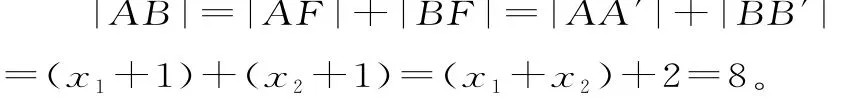
评注:在抛物线中过焦点的弦称为“焦点弦”。抛物线的定义本身也是抛物线最本质的性质,在求焦点弦长时起着至关重要的作用。

变式2:若直线l:y=k x-2交抛物线y2=8x于A、B两点,且A B的中点为M(2,y0),求y0及弦A B的长。

分析:对A,B两点坐标设而不求,进而利用韦达定理和弦长公式|xA-xB|来求y0及弦A B的长。

解:把y=k x-2代入y2=8x,得:

k2x2-(4k+8)x+4=0。

设A(x1,y1),B(x2,y2)。

因为A B中点为M(2,y0),所以x1+x2=4,即,解得k=2或k=-1。

又Δ=1 6k2+6 4k+tu-1 6k2＞0,则k＞-1,k=2。

此时直线的方程为y=2x-2。

因为M(2,y0)在直线上,所以y0=2。

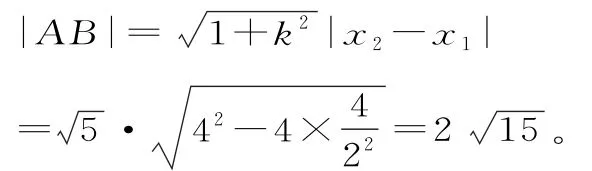
评注:抛物线弦的中点坐标和方程的两根之和的密切联系是解决中点弦问题的关键,方程思想也是解析几何的核心思想。

变式3:(1)已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A、B两点。若A B的中点为(2,2),则直线l的方程为____。

(2)过抛物线y2=x上的点A(4,2)作倾角互补的两条直线A B、A C,交抛物线于B、C,则直线B C的斜率为____。

分析:(1)直线l过点(2,2),故要求直线直线l的方程,只需求直线l的斜率。又(2,2)是弦A B的中点,故宜采用点差法。(2)本小题虽未涉及弦的中点,但A,B,C三点都在抛物线上,并探究的是三条弦的斜率关系,故也宜采用点差法。

解:(1)因为抛物线C的顶点在坐标原点,焦点为F(1,0),所以,抛物线的方程为y2=4x。

设A(x1,y1),B(x2,y2),则有y1+y2=

①-②得:

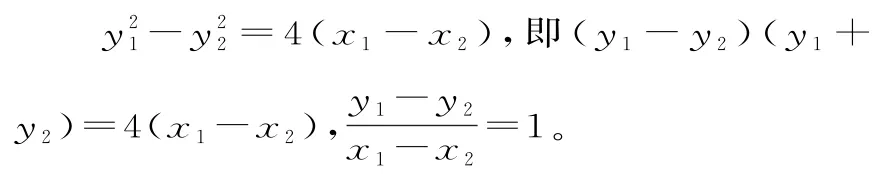
所以直线l的斜率为1,且过点(2,2),直线方程为y-2=x-2,即y=x。

(2)设B(x1,y1),C(x2,y2),代入抛物线的方程得:

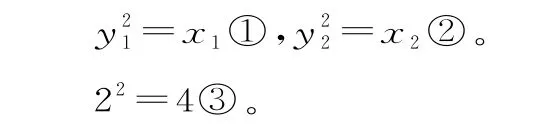
①②两式作差整理得:

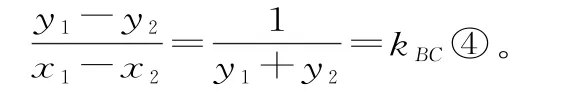
①③两式作差整理得:

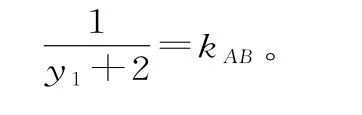
又因为kAC=-kAB,所以整理得y1+y2=-4。

评注:在抛物线y2=2m x(m≠0)中,若直线l与抛物线相交于M、N两点,点P(x0,y0)是弦MN的中点,弦MN所在的直线l的斜率为kMN,则kMN·y0=m。利用这个结论解有关问题,可以大大减少运算量。