全国名校抛物线拔高卷（B 卷）答案与提示

一、选择题

1.A 2.C 3.D 4.C 5.D 6.D 7.B.A 9.D 10.C 11.B 12.B 13.D 14.C 5.A 16.D 17.C 18.A 19.C 20.C 1.C 22.A 23.C 24.C 25.B 26.B 7.A 28.C 29.B 30.D 31.C 32.C 3.B 34.D

二、填空题

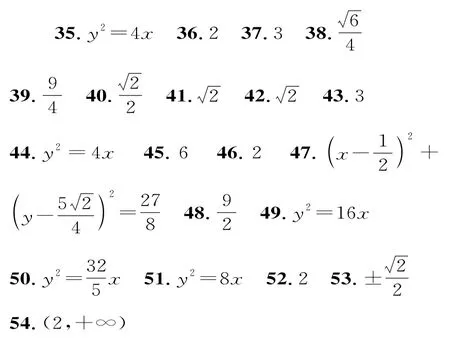
三、解答题

55.(1)已知动点E到定点D(1,0)的距离等于点E到直线x=-1的距离,由抛物线的定义知E点的轨迹是以D(1,0)为焦点,以x=-1为准线的抛物线,故曲线C的方程为y2=4x。

(2)由题意可知直线l1,l2的斜率存在,倾斜角互补,则斜率互为相反数,且不等于零。

设A(x1,y1),B(x2,y2),直线l1的方程为y=k(x-1)+2,k≠0;

直线l2的方程为y=-k(x-1)+2。

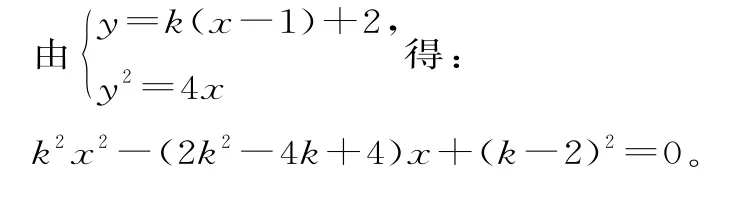
已知此方程一个根为1,故x1×1=

所以,直线A B的斜率为定值-1。

56.(1)设C(x0,y0),则由抛物线的定义得

所以p=2,抛物线的方程为x2=4y。

(2)因为|BM|=|BN|,所以点B在线段MN的中垂线上。

设B(x1,y1),则M(x1-2,0),N(x1+2,0)。

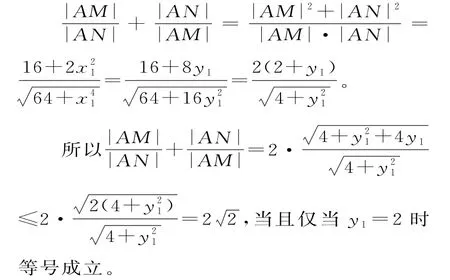
此时x1=±22。

57.(1)设抛物线D的方程为x2=2p y

所以抛物线D的方程是x2=4y。

(2)设切线y-y0=k(x-x0),即k x-y+y0-k x0=0。

设两切线斜率分别为k1,k2,则k1+k2

所以切线与x轴围成的三角形面积S的最小值为32。

58.(1)由题意可设抛物线方程为x2=2p y,其准线方程为

所以抛物线的方程为x2=4y。

(2)由(1)可得点M(4,4)。

设直线MD的方程为:y=k(x-4)+4。

设D(x1,y1),E(x2,y2),则xM·x1=1 6k-tu。

所以直线D E的方程为y-4(k-1)2=

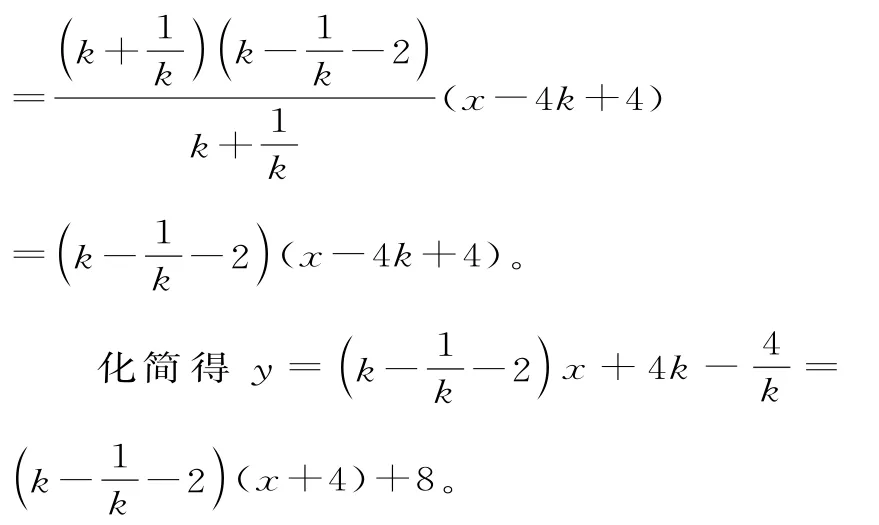
故直线D E过定点(-4,8)。

设C(x1,y1),G(x2,y2),直线C G的方程为

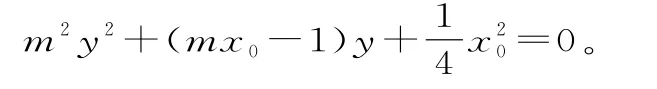
因为G为△A B C的重心,所以y1=y2。

60.(1)因为抛物线C1的焦点坐标是,所以过焦点且在x轴上截距为2的

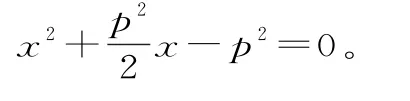
设点Q(xQ,yQ),N(xN,yN)。

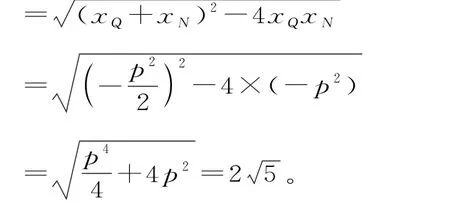
解得p=2。

所以抛物线C1的方程为x2=4y。

(2)设点A(x1,y1),B(x2,y2)(x1＞0,2＜0),设过A点的切线方程为y-y1=1(x-x1),联立抛物线方程x2=2p y,利用新的方程的判别式等于零,可得同理设过B点的切线的斜率为k2,解得k2=

因此,x1,x2是方程x2-2a x-4p2=0的两根,则x1+x2=2a,x1x2=-4p2。

61.(1)易知F(1,0),设A B:x=λ y+1。

且由(1)知y1y2=-4,y1+y2=4λ。

代入①得:

|MN|≥4,仅当λ=0时,|MN|取最小值4。

综上所述,|MN|的最小值是4。

故轨迹C的方程为y2=2x。

又t1≠t2,故t1t2=-1。

将t1t2=-1代入上式,可得(x+2)2+y2-2(t1+t2)y-4=0。

令y=0,则x=0或x=-4。

故以MN为直径的圆被x轴截得的弦长为定值4。

63.(1)因为圆N:(x+1)2+y2=2,所以圆心N为(-1,0),半径r=2。

设A(x1,y1),B(x2,y2),当直线l的斜率为-1时,设l的方程为y=-x+m,则:

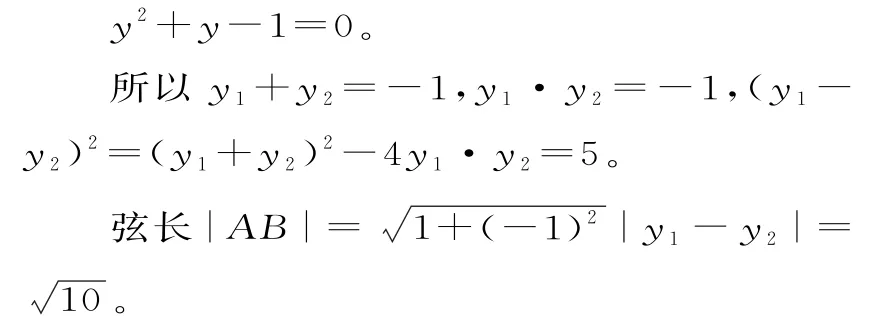
(2)i)当直线l的斜率不存在时,因为直线l是圆N的切线,所以l的方程为-1。与y2=x联立,可得(y1+y2)+1=5-32≠0,不符合题意 。

i i)当直线l的斜率存在时,设直线l的方程为y=k x+m,即k x-y+m=0(k≠0)。

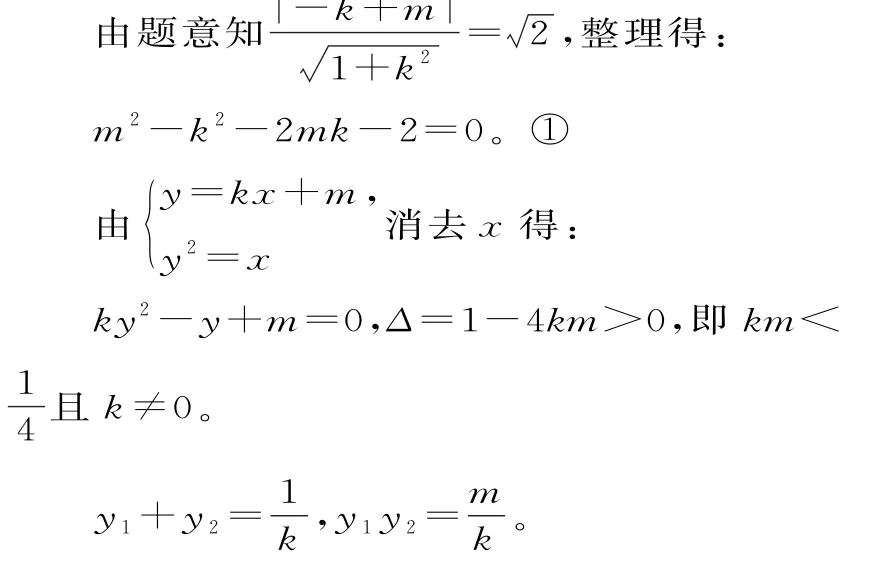
因为点M和点N关于直线y=x对称,所以M的坐标为(0,-1)。

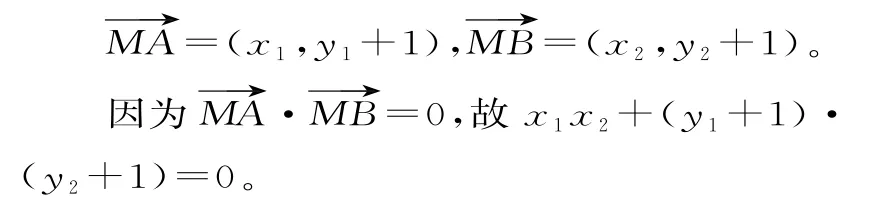
A(x1,y1),B(x2,y2)在直线y=k x+m上代入并化简,得(1+k2)y1y2+(k2-m)·(y1+y2)+m2+k2=0。

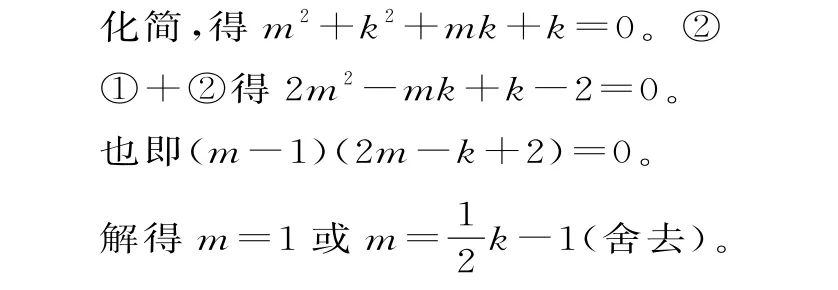
综上所述,存在满足条件的直线,其方程为y=-x+1。