椭圆焦点三角形的性质探究与应用———椭圆的“第三定义”

■安徽省安庆市第一中学 洪汪宝

我们知道,椭圆上任意一点(除去长轴端点)与两焦点所构成的三角形称为椭圆的焦点三角形。那么该三角形有哪些特殊的性质呢?本文对椭圆的焦点三角形的性质进行探究并举例说明其应用。

一、性质探究

为了研究问题的方便,我们以焦点在x轴上的椭圆为例。有兴趣的读者,可模仿推导焦点在y轴上的椭圆的情况。

性质1:△P F1F2的周长为定值,其值为a+2c。

性质2:△P F1F2的面积为c|y0|,其最大值为b c,当点P位于短轴端点时焦点三角形的面积取到最大值。

性质3:若∠F1P F2=α,则△P F1F2的面积为

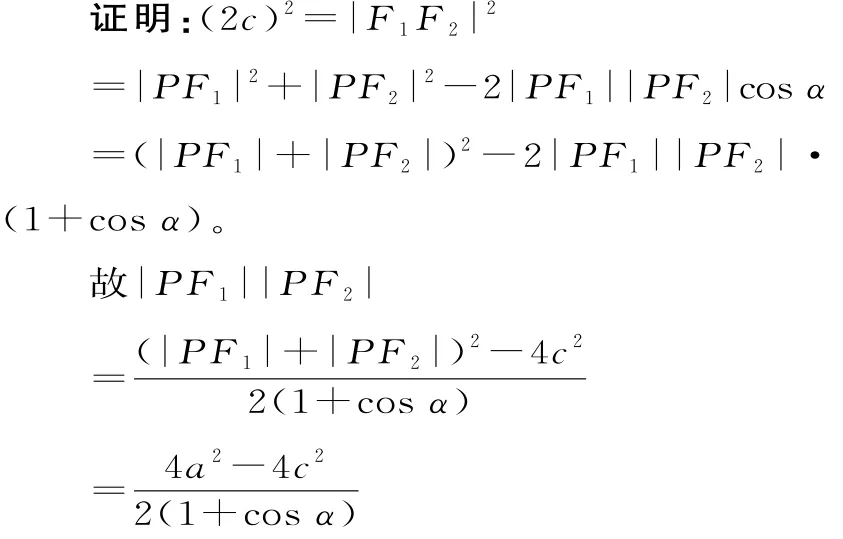
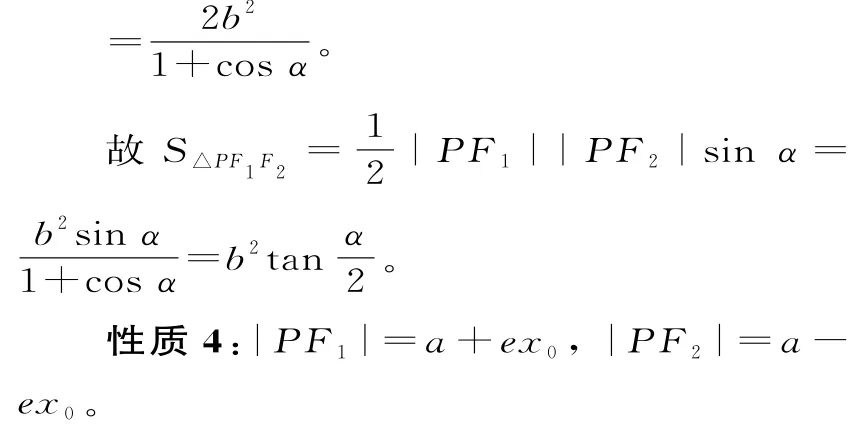
证明:设椭圆的右准线方程为,根据椭圆的第二定义知,于是可得根据椭圆的第一定义知

根据此性质可知椭圆上的点到焦点的最大距离为a+c,最小距离为a-c,此时该点是椭圆长轴的端点。

性质5:若∠F1P F2=α,则当点P位于上、下顶点时,α最大。

证明:由余弦定理知:

当且仅当|P F1|=|P F2|即当点P位于上、下顶点时c o sα取到最小值,又余弦函数在[0,π]上单调递减,此时α最大。

性质6:设∠P F1F2=β,∠P F2F1=θ,则椭圆的离心率

证明:由正弦定理知

性质7:如图1,作∠F1P F2的补角的平分线P F,过F2作P F的垂线,垂足为D点,则点D的轨迹是一个圆。

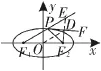
图1

证明:延长F2D交F1P的延长线于点E,连O D。

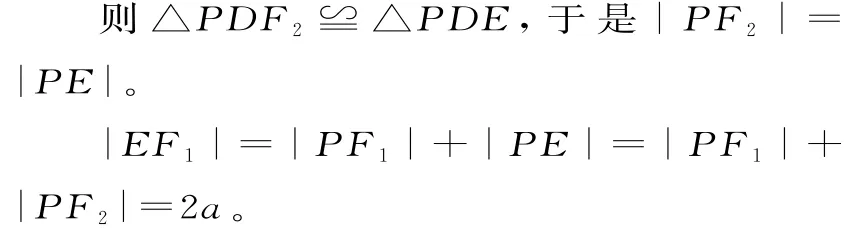
又O D为△F1F2E的中位线,则|O D|=a。

所以点D的轨迹是一个以原点为圆心,半径为a的圆。

性质8:如图2,作圆与线段F1P的延长线、线段F2P、线段F1F2的延长线分别切于点D、E、F,则点F为椭圆的右顶点。

图2

证明:根据定义知

故2a+2c=2(xF-(-c))。

解得xF=a。

所以点F为椭圆的右顶点。

二、性质应用

例1已知F1,F2是椭圆的左、右焦点,P是椭圆上一点,且则△P F1F2的面积为____。

解:根据性质3可知△P F1F2的面积为9 t a n4 5°=9。

例2已知椭圆0)的两个焦点分别为F1,F2,若椭圆C上存在点P使∠F1P F2=120°,则该椭圆C的离心率的取值范围为____。

解:由性质5的所得结论c o sα≥1-2e2知c o s1 段 °≥1-2e2,解得

例3已知F1,F2是椭圆的左、右焦点,P是椭圆上一点,若△P F1F2为直角三角形,则这样的点P有____个。

解:若点P为直角顶点,根据性质5由a=2b知P为上下顶点;若F1为直角顶点,过F1作F1F2的垂线交椭圆于两点,此两点即为所求;同理,若F2为直角顶点,则满足条件的点P也有两个。综上所述,符合条件的点P有6个。

例4已知椭圆0)的两个焦点分别为F1,F2,若椭圆C上存在点P使∠P F1F2=75°,∠P F2F1=15°,则该椭圆C的离心率为____。

解:由性质6知该椭圆的离心率为

例5椭圆的左焦点为F,直线x=m与椭圆相交于点A、B,当△F A B的周长最大时,△F A B的面积是____。

解:设该椭圆的右焦点为F1,则△F A B的周长为|A F|+|B F|+|A B|≤|A F|+|B F|+|A F1|+|B F1|=8,当且仅当直线x=m经过点F1时等号成立,此时|A B|=3,△F A B的面积为