全国名校双曲线拔高卷(A卷)
■江苏省泰州市兴化第一中学 刘伟华
一、选择题

2.中心在原点,对称轴为坐标轴的双曲线C的两条渐近线与圆(x-2)2+y2=1都相切,则双曲线C的离心率是( )。


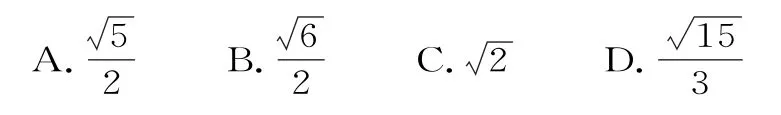
5.设双曲线,离心率e=2,右焦点为F(c,0)。若方程a x2-b x-c=0的两个实数根分别为x1,x2,则点P(x1,x2)在圆x2+y2=8的( )。
A.外部 B.圆周上
6.设F1、F2是双曲线C:>0,b>0)的左、右焦点,A为左顶点,点P为双曲线C右支上一点,|F1F2|=10,P F2⊥O为坐标原点,则

7.已知M(x0,y0)是双曲线=1上的一点,F1、F2是双曲线C的两个焦点,若则y0的取值范围是( )。



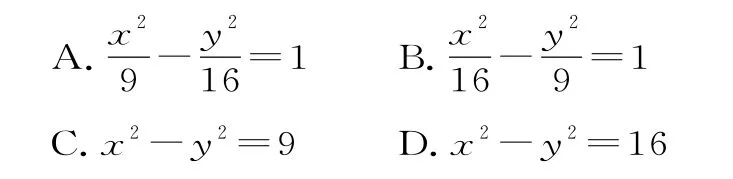
11.已知定点F1(-2,0),F2(2,0),N是圆O:x2+y2=1上任意一点,点F1关于点N的对称点为M,线段F1M的中垂线与直线F2M相交于点P,则点P的轨迹是( )。
A.直线 B.圆
C.椭圆 D.双曲线
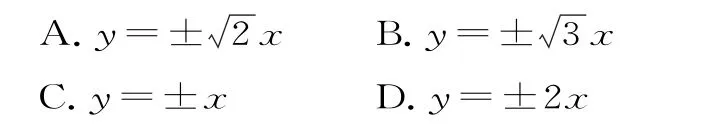

14.设F1、F2是双曲线>0,b>0)的左、右焦点,P是双曲线C右支上一点,若|P F1|+|P F2|=6a,且△P F1F2的最小内角为30°,则双曲线C的离心率为( )。
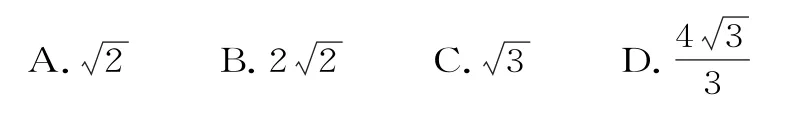

16.已知F1、F2是双曲线>0,b>0)的左、右焦点,P是双曲线上一点,且P F1⊥P F2,若△P F1F2的内切圆半径为,则该双曲线的离心率为( )。
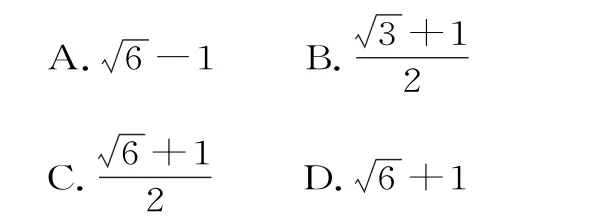
17.已知F1、F2分别是双曲线的左、右焦点,若双曲线E上存在一点P使得,则双曲线E的离心率的取值范围是( )。
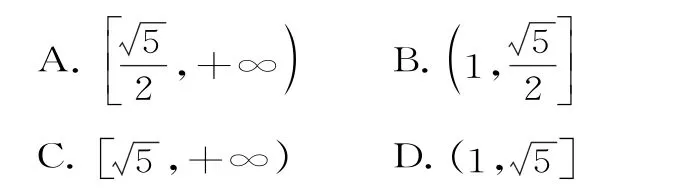

A.(1,2) B.(2,+∞)
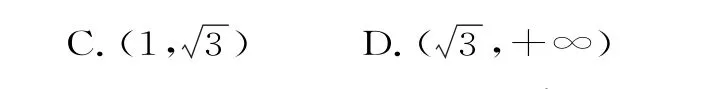

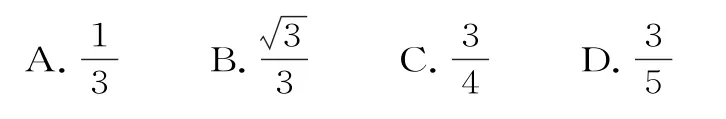
22.如 图1,F1、F2是双曲线0,b>0)的左、右焦点,过F1的直线l与双曲线C的左、右两支分别交于点A、B。若△A B F2为等边三角形,则双曲线的离心率为( )。

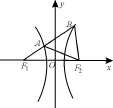
图1
23.已知F1、F2分别为双曲线1(a>0,b>0)的左、右焦点,P为双曲线右支上的任意一点,若的最小值为8a,则双曲线的离心率e的取值范围是( )。
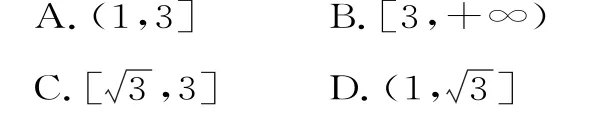
24.设双曲线的左、右焦点分别为F1、F2,过F1作倾斜角为的直线与y轴和双曲线的右支分别交于点A、B,若,则该双曲线的离心率为( )。

25.若双曲线C:x2-y2=1的右顶点为A,过A的直线l与双曲线C的两条渐近线交于P,Q两点,且,则直线l的斜率为( )。



28.已知F1、F2是双曲线>0,b>0)的左、右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线的另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是( )。
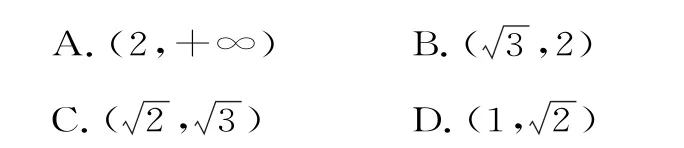
29.已知双曲线0),A1、A2是实轴顶点,F是右焦点,B(0,b)是虚轴端点,若在线段B F上(不含端点)存在不同的两点Pi(i=1,2),使得△PiA1A2(i=1,2)构成以A1A2为斜边的直角三角形,则双曲线离心率e的取值范围是( )。
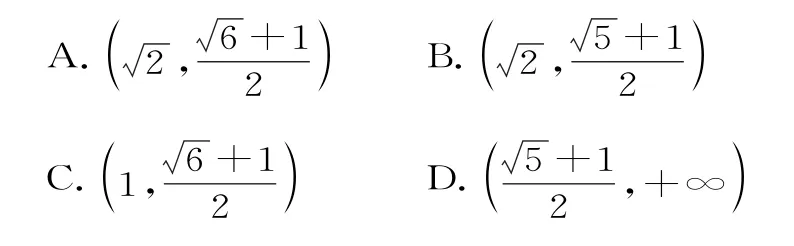
的一条渐近线上位于第一象限内的点,∠A O F=∠O A F,△A O F的面积为33,则双曲线C的方程为( )。
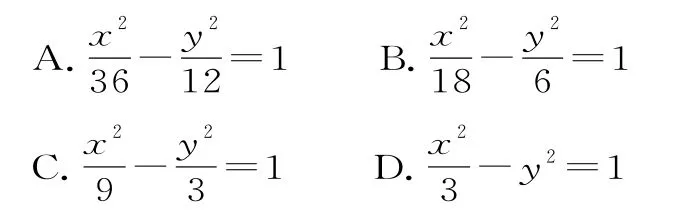
31.已知椭圆和双曲线有共同焦点F1、F2,P是它们的一个交点,∠F1P F2=60°,记椭圆和双曲线的离心率分别的最小值是()。

′1,且F′1是以F2为圆心,以半焦距c为半径的圆上的一点,则双曲线C的离心率为( )。
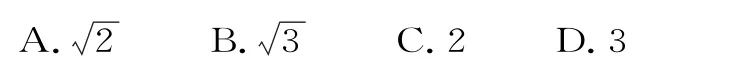


35.已知F1,F2是椭圆与双曲线的公共焦点,P是它们的一个公共点,且|P F2|>|P F1|,椭圆的离心率为e1,双曲线的离心率的最小值为( )。

A.3 B.4
C.5 D.与点P的位置有关
A.8 B.4 C.2 D.1
38.已知F1,F2是椭圆和双曲线的公共焦点,且A,B两点为椭圆C1,双曲线C2在第二、四象限的公共点,若四边形A F1B F2为矩形,则双曲线C2的离心率为( )。

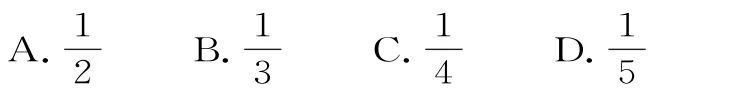
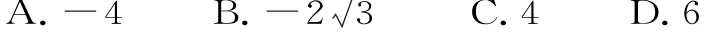
二、填空题
42.设F1、F2分别为双曲线=1的左、右焦点,P为双曲线C在第一象限上的一点,若,则△P F12F内切圆的面积为____。
43.过点M(-6,3)且和双曲线x2-2y2=2有相同的渐近线的双曲线方程为
44.如图2所示,椭圆中心在坐标原点,F为左焦点,A,B分别为椭圆的右顶点和上顶点,当F B⊥A B时,其离心率为此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于____。
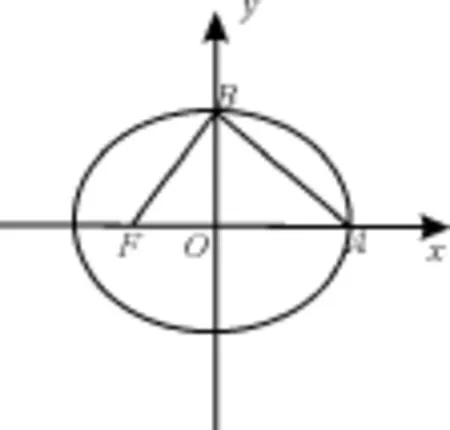
图2
51.在平面直角坐标系中,O为坐标原点,过双曲线C:x2-y2=a2(a>0)的右顶点P作射线l与双曲线C的两条渐近线分别交于第一象限的点M和第二象限的点N,且的面积为S=3,则a=____。
56.若F1、F2分別是双曲线(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线的左支上,点M在直线上,且 满 足),则该双曲线的离心率为
59.如图3,等腰梯形A B C D中,A B∥C D且A B=2,A D=1,D C=2x(x∈(0,1))。以A,B为焦点,且过点D的双曲线的离心率为e1;以C,D为焦点,且过点A的椭圆的离心率为e2,则e1+e2的取值范围为

图3
三、解答题
60.求满足下列条件的双曲线的标准方程:
61.已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率,且过点(4,
(1)求双曲线的方程。
(2)若点M(3,m)在双曲线上,求证:MF1⊥MF2。
(1)求证:点P到双曲线C的两条渐近线的距离的乘积是一个常数;
(2)设点A的坐标为(3,0),求|P A|的最小值。
63.已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为,右焦点为F(5,0),双曲线的实轴为A1A2,P为双曲线上一点(不同于A1,A2),直线A1P,A2P分别与直线交于M,N两点。
(1)求双曲线的标准方程;
64.已知动圆P过点F2(2,0)并且与圆F1:(x+2)2+y2=4相外切,动圆圆心P的轨迹为C。
(1)求曲线C的轨迹方程;
(2)过点F2(2,0)的直线l1与轨迹C交于A、B两点,设直线,点D(-1,0),直线A D交l于M,求证:直线BM经过定点(1,0)。
65.已知中心在原点的双曲线C的右焦点为(2,0),实轴长
(1)求双曲线的方程;
(1)求曲线E的方程;
(2)设曲线E′表示曲线E的y轴左边部分,若直线y=k x-1与曲线E′相交于A,B两点,求k的取值范围;

