解题非常道思维顺势为———巧用并集妙解题

■江西省丰城中学 吴爱龙 熊华芳

解题是一种思维活动,当解题思路正面受阻时,人们便抛弃现有思路,迫不及待地去寻找另一思维方向。于是乎,“正难则反思想”、“补集思想”、“等价转化思想”便蜂拥而至。但这些方法从某个层面上说,是不是舍本逐末或不敢“正视”呢?笔者认为,解题时应具体问题具体分析,而不应刻意追求某种模式解法而束缚自己的思维。本文借助集合与简易逻辑知识说明这一拙见。

例1 已知集合A={x|x2+4a x-4a+3=0},集合B={x|x2+(a-1)x+a2=0},集合C={x|x2+2a x-2a=0},若三个集合至少有一个非空,求a的取值范围。

分析1:“三个集合至少有一个非空”,正面讨论情形较多,从反面入手。

解法1:假设三个集合均为空集,即三个方程均无实根,则:

分析2:三个集合至少一个非空,包括恰有一个非空、恰有2个非空、3个均非空,共7种情形,反面是三个集合均为空集,仅1种情形。看似正面求解会比反面求解复杂,其实不然。众所周知,数学简易逻辑中的“或”不同于生活中的“或”,是带“兼有性”的“或”,指的是两个或多个句子中,至少一个成立。反映到集合中,“或”可以理解为“并”,即两个或多个集合的并集。若能充分理解“或”字含义,巧用取并集思想亦可快速解题。

解法2:正面考虑,需三个方程至少一个有解,分别解下面三个不等式Δ1=(4a)2-4(3-4a)≥0,或Δ2=(a-1)2-4a2≥0,或Δ3=(2a)2+8a≥0,并求“并”得a的取值范围为)。因此,三个集合至少有一个非空时,a的取值范围为

点评:解法2,看似要分三大类、七小类进行讨论,但由于巧妙地把“或”灵活地演绎成“并”,正面挑战亦然成功。两种解法孰繁孰简无需多言!

例2设函数的定义域为A,若命题p:3∈A;命题q:5∈A,至少有一个是真命题,求实数a的取值范围。

分析:若从正面做有三种情况,比较复杂,所以考虑先求反面情况,再求补集即可。

若命题p:3∈A与命题q:5∈A都是假命题,则3∉A且5∉A,即:

所以命题p:3∈A与命题q:5∈A中至少有一个是真命题时,实数a的取值范围是1＜a＜25。

解法2:函数有定义域,必须满足＞0,即(a x-5)(x2-a)＞0。

若q:5∈A为真,则(5a-5)(25-a)＞0⇒1＜a＜25。

所以命题p:3∈A与命题q:5∈A中至少有一个是真命题时,实数a的取值范围是＜a＜25。

点评:正面三种情况,被一“并”解决,顺理又成章,不见得比反面求解更复杂。

例3已知命题p:关于x的不等式x2+(a-1)x+a2＜0有实数解,命题q:指数函数y=(2a2-a)x在R上单调递增。

(1)若“p且q”为真命题,求实数a的取值范围;

(2)若“p或q”为真命题,“p且q”为假命题,求实数a的取值范围。

分析:(1)“p且q”为真命题,则p真,q真;(2)“p或q”为真命题,则p,q至少有一个为真。

解法1:(1)p真⇔Δ=(a-1)2-4a2＞

q真⇔2a2-a＞1⇔a＜

解得-1＜a＜-1。2

(2)由题意知p,q一真一假。

解法2:,过程略。

所以“p或q”为真,“p且q”为假等价于:

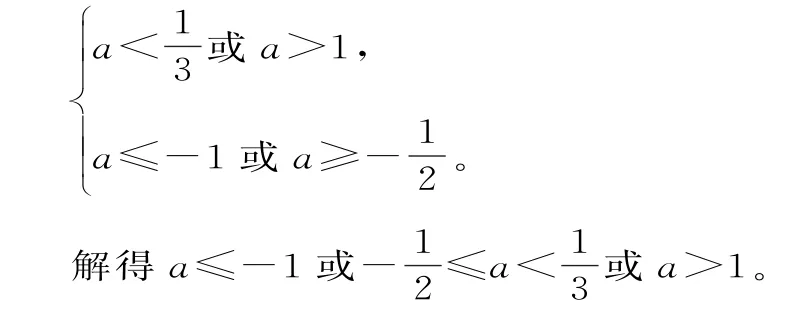
点评:解法1将问题分为两类进行讨论,复杂!解法2直视条件,顺势而为,简单!

例4已知命题p:函数f(x)=的定义域为R;命题q:不

解析:易得命题p为真时,a＞2;

命题q为真时,a≥1。

求并便知命题“p或q”为真命题时,a≥1。又命题“p且q”为假命题时,a≤2,所以满足条件的实数a的取值范围是1≤a≤2。

一条山路看似荆棘满布,或许是捷径;一种思路好像障碍重重,顺势而为或许是妙想!迂回是一种智慧,面对却是一种勇气。学好数学要有智慧,但更多时候靠的是信心和勇气。