一类非线性矩阵方程的正定解

房亮，刘三阳

（西安电子科技大学 数学与统计学院，陕西西安710071）

考虑非线性矩阵方程：

其中Ai,Bj,i=1,2,…,m,j=1,2,…,n是n×n非奇异复矩阵，Q为Hermite正定矩阵。矩阵A*表示A的共轭转置。此类非线性矩阵方程来源于随机控制、动态规划、统计学、随机过程等实际应用问题［1-5］。当m=n=1时，非线性矩阵方程（1）是随机控制理论中一类特殊的随机代数Riccati微分方程［1］。当所有Ai=0,i=1,2,…,m时，方程（1）在一类最优插值问题中起重要作用［2，5］。

矩阵方程（1）正定解的研究是近些年数值代数的研究热点之一，在一些特殊情形下，已有诸多研究结果。如文献［6-9］深入研究了X±A*X-1A=Q的正定解及其扰动问题。文献［10-11］提供了几种求解非线性矩阵方程=I的迭代方法。对减号方程，文献［5］证明了其必有唯一正定解，文献［12-13］分别用矩阵微分的方法讨论了唯一正定解的扰动问题。最近，BEREIG［14］研 究 了 线 性 矩 阵 方 程 X+A*XA- B*XB=Q正定解的存在性和唯一性问题。当m=n=1时，文献［15-17］分别讨论了非线性矩阵方程

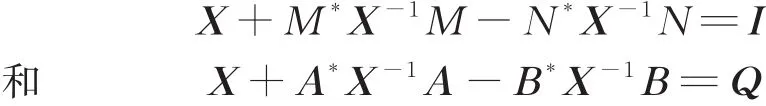
（其中Q正定）正定解的存在性及求解的迭代算法。

在此基础上，本文考虑更一般的矩阵方程（1），其中m,n≥1。利用广义Lakshmikantham-Bhaskar不动点定理，得到方法（1）存在唯一正定解的条件，并给出唯一正定解的迭代算法。同时，讨论正定解的扰动问题，给出一个易于计算的扰动上界，并推导其Rice条件数的显式表达式。

1 符号与引理

文中，Cn×n,Hn×n和H+(n)分别表示n × n阶复矩阵、n×n阶Hermite矩阵和Hermite正定矩阵的集合。A≥0(A＞0)表示A为Hermite半正定（正定）矩阵。σ1(A)和σn(A)分别表示A的最大和最小奇异值；λ1(A)和λn(A)分别表示A的最大和最小特征值。对A,B∈Hn×n，记A≥ B(A＞B)，若A-B ≥ 0(＞ 0)；记

符号tr(A)表示矩阵A的迹，‖·‖tr表示迹范数(A)，其 中 σi(A),i=1,2,…,n 为矩阵A的奇异值。易知‖·‖tr是酉不变的，且对Hermite半正定矩阵A，有‖A‖tr=tr(A)。如果无特殊说明，符号‖·‖表示谱范数（即 ‖A‖=σ1(A)）。显然，对任意正定矩阵Q，都有‖Q‖=λ1(Q)且 ‖Q-1‖-1= λn(Q)。

引理1［3］令f为 (0,∞)上的一个单调算子，且A,B是2个以a为下界的正算子，即对正数a有A＞ aI和B＞ aI。若存在f′(a)，则对任意酉不变范数 ‖ ·‖都有

引理2［3］设A,B均为n× n半正定矩阵。则

令(X,≤ )为一个偏序集，在积空间 X×X上定义偏序：对任意(x,y),(u,v)∈X×X,

称映射F:X×X→X具有混合单调性，若F(x,y)关于x递增，同时关于y递减，即对任意x1≤x2,y2≤ y1，有 F(x1,y1)≤ F(x2,y2)。

若 x=F(x,y),y=F(y,x)，称 (x,y)是 F的耦合不动点。

引理3［18］（广义耦合不动点定理）令(X,≤ )为一个偏序集，设X上有一个距离d，使得(X,d)是一个完备度量空间。令F:X×X→X为混合单调映射，且存在常数δ∈[0,1)，使得对任意x≥u,y≤v,有

假设：

（i）存 在 x0,y0∈ X 使 得 x0≤ F(x0,y0)，y0≥F(y0,x0)，或者 x0≥ F(x0,y0),y0≤ F(y0,x0)。

（ii）X×X中的每对元素都有下界和上界，即对 每 2 个 (x,y),(x∗,y∗)∈X × X 均 存 在(u,v)∈ X × X可与(x,y),(x∗,y∗)比较。

2 正定解的存在性

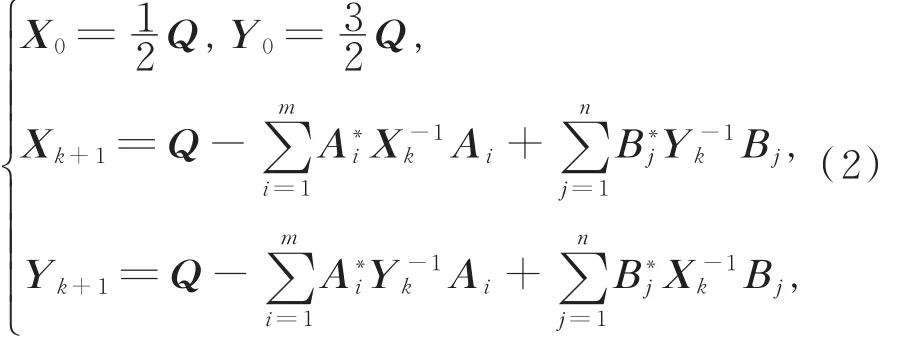
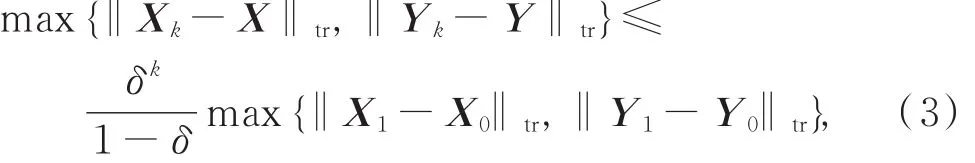
其中，

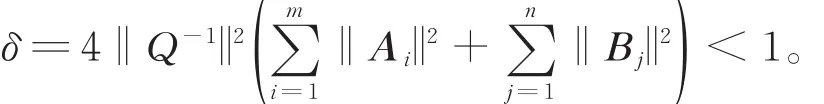
证明考虑映射：对X,Y∈Ω，

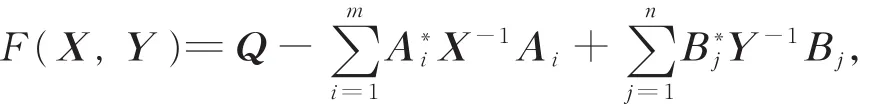
Ω上的连续映射。证明分为5步：

（i）由条件易知

从而对任意X,Y∈Ω，

可见F(X,Y)∈ Ω，也即F:Ω × Ω → Ω。

（ii）对 ∀X1,X2,Y1,Y2∈ Ω，X1≤ X2，Y1≥ Y2，

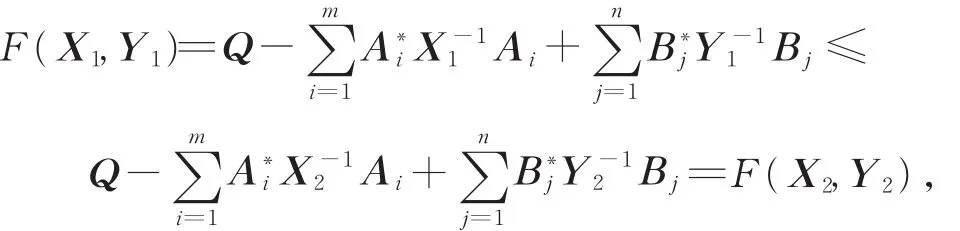
可见F(X,Y)具有混合单调性。

（iii） 由 引 理 1 和 引 理 2， 对 任 意X,Y,U,V∈Ω，满足

有

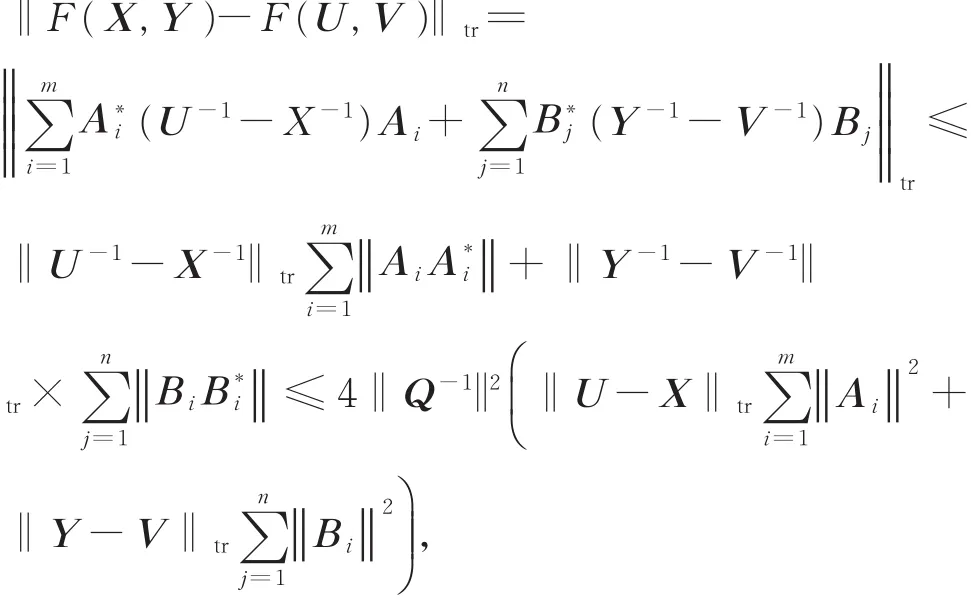
同理有

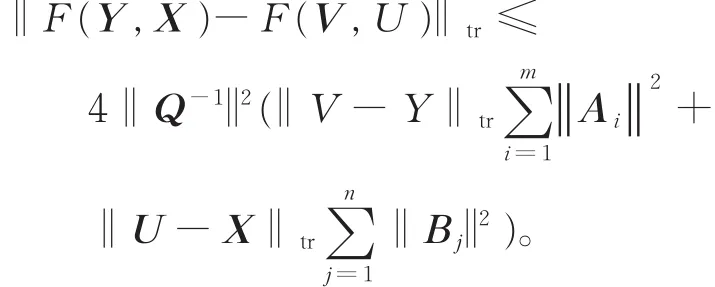
从而

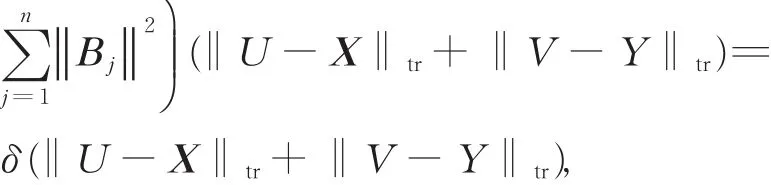
其中δ已由式（3）给出。

有

类似可得

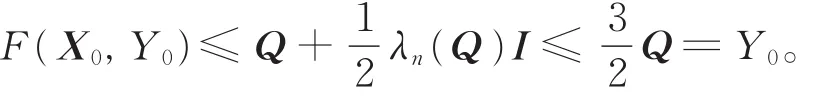
（v）任给 (X,Y)，(X*,Y*)∈ H+(n)× H+(n)，令

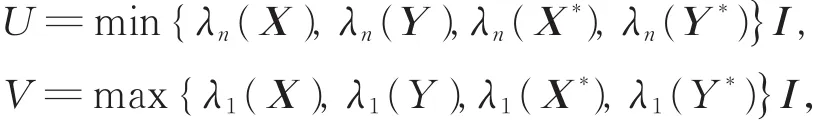
不 难 看 出 (U,V)≤(X,Y)，且 (U,V)≤(X*,Y*)，即H+(n)×H+(n)中的每对元素都有下界。

3 正定解的扰动分析

考虑扰动方程：

3.1 扰动上界

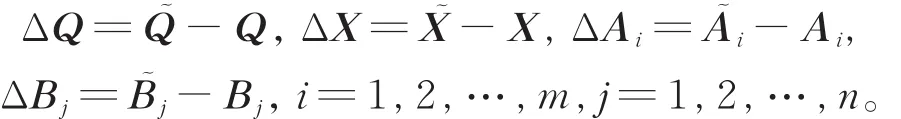
定理2 令

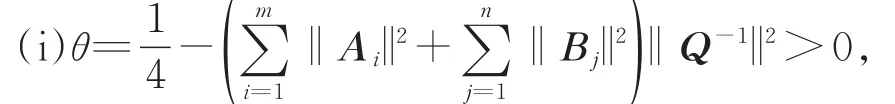
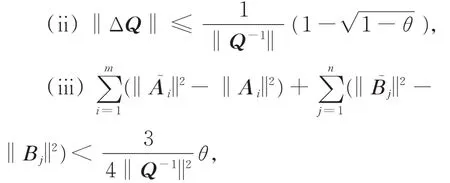
则非线性矩阵方程（1）和其扰动方程（4）分别有唯一正定解X和X͂，且

证明 由θ＞0及定理1知，矩阵方程（1）有唯一正定解X≥Q。由 θ＜ 1及

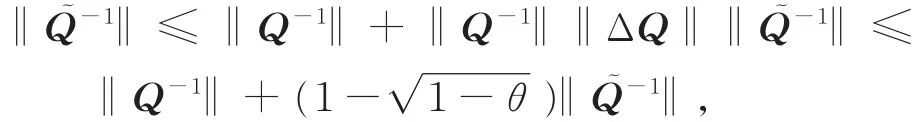
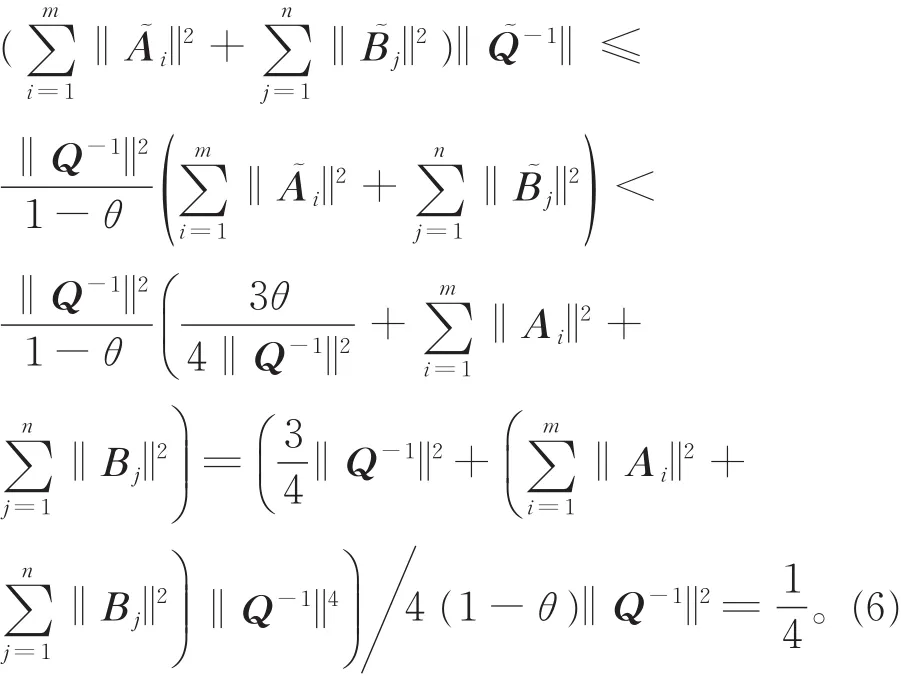
再证估计式（5）：

用式（4）减去式（1）可得

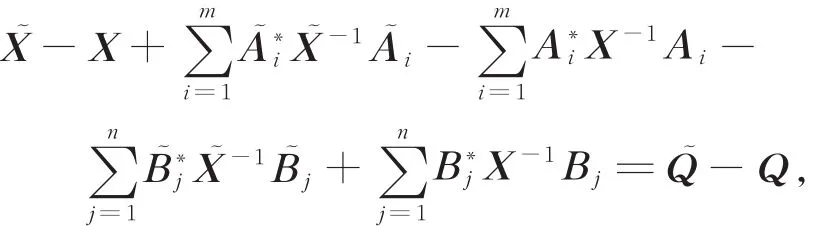
整理得

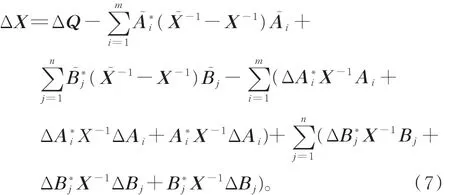
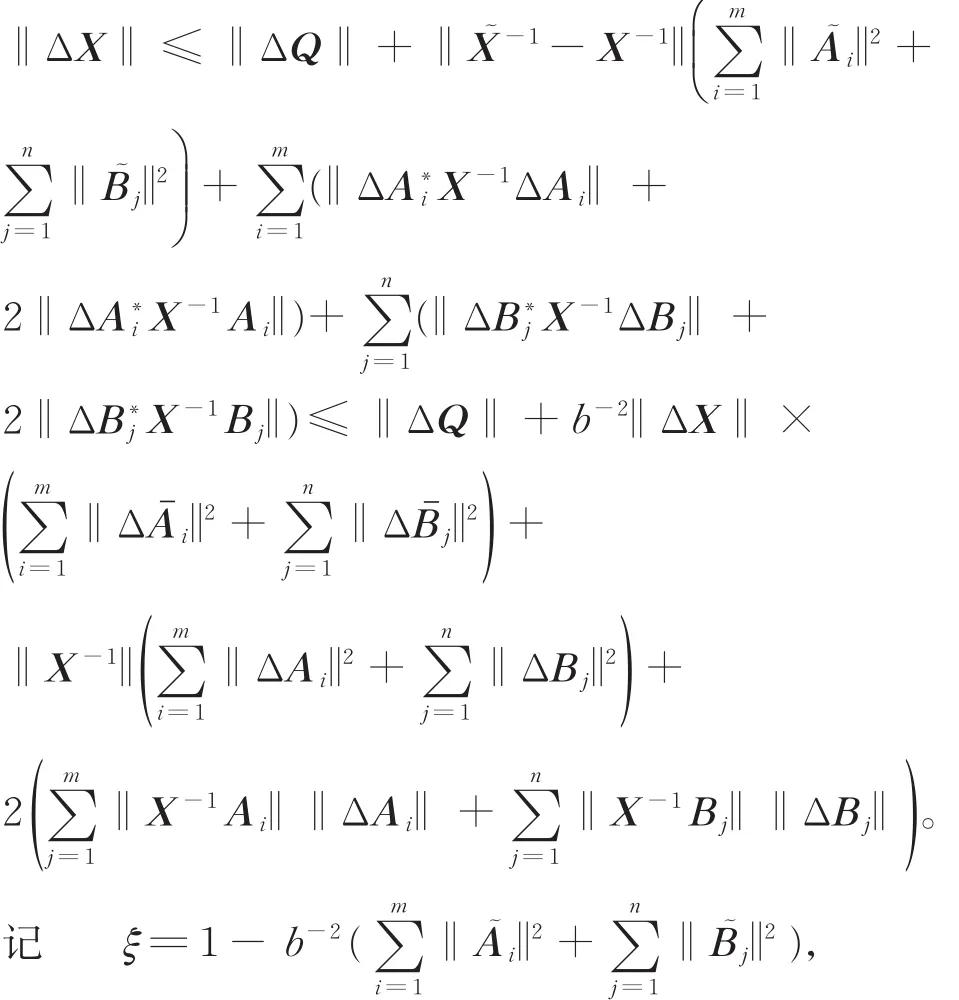
3.2 Rice条件数

下面给出正定解Rice条件数的显式表达式。

情形1复数域情形

由定理2知，若‖ΔAi‖,‖ΔBj‖,i=1,2,…,m,j=1,2,…,n和‖ΔQ‖充分小，则扰动方程（4）有唯一正定解͂。

其中，

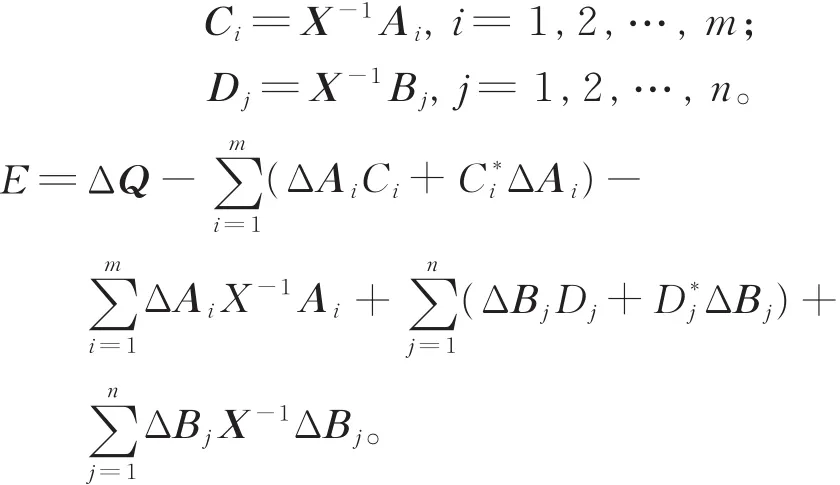
记h(Δ X)为ΔX的高阶无穷小量：

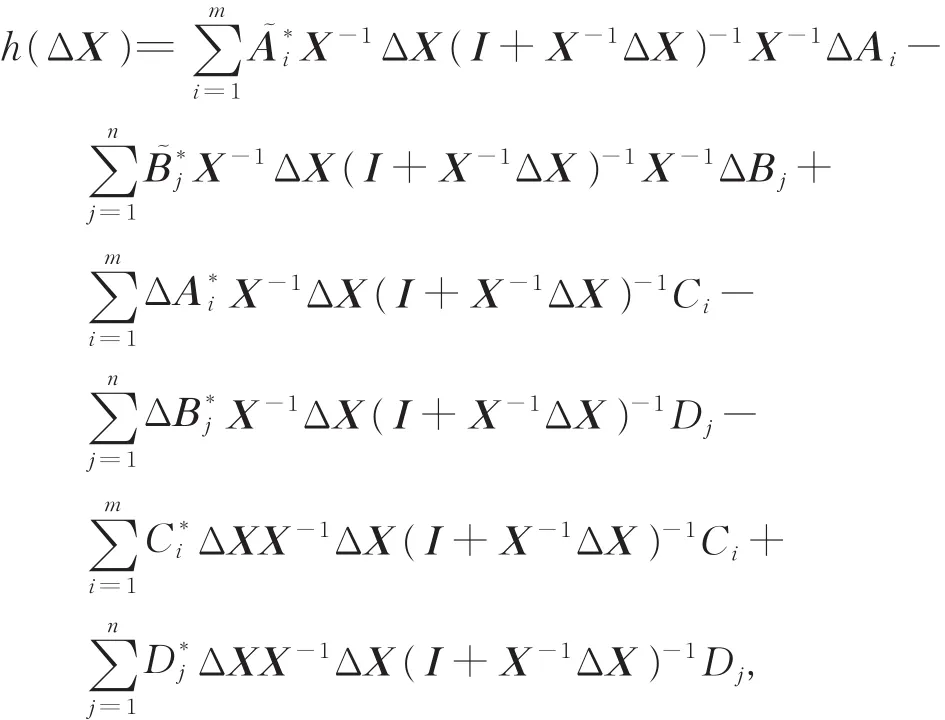
定义线性算子L：Hn×n→ Hn×n：

对任意W ∈ Hn×n，

定义算子M:Hn×n→ Hn×n:

则式（9）等价于W-MW=V。

于是‖M‖＜1，I-M可逆。从而对任意矩阵V ∈ Hn×n，方程（9）有唯一解，故 L可逆。于是式

（8）可改写为

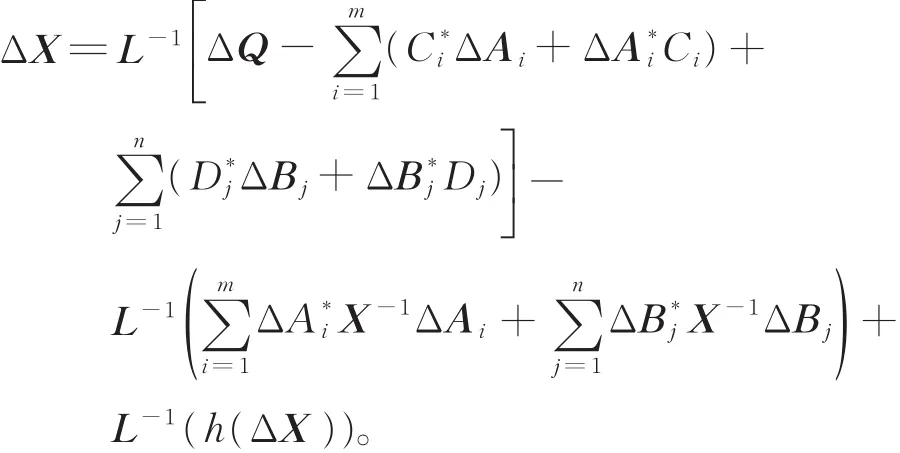
则有

根据 Rice的条件数理论［19］，定义矩阵方程（1）的唯一正定解的条件数为

其中，ξ,μ1,μ2,...,μm,η1,η2,...,ηn,ρ均为正参数。在式（10）中 取 ξ=μ1=…=μm=η1=…=ηn=ρ=1，可得绝对条件数Cabs(X)；取

得相对条件数Crel( X )。

令L为算子L的矩阵，易得

记

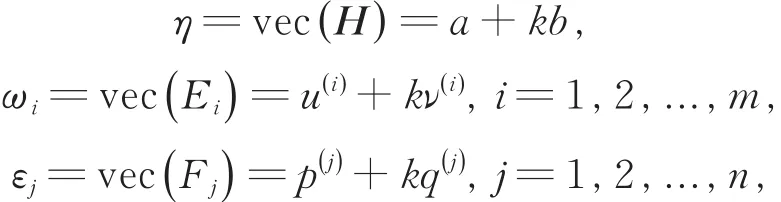
其中k为满足k2=-1的虚数单位。

对i=1,2,…,m,j=1,2,…,n，令

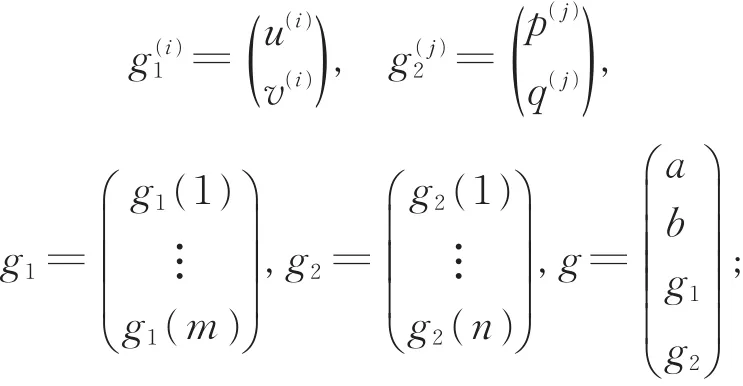
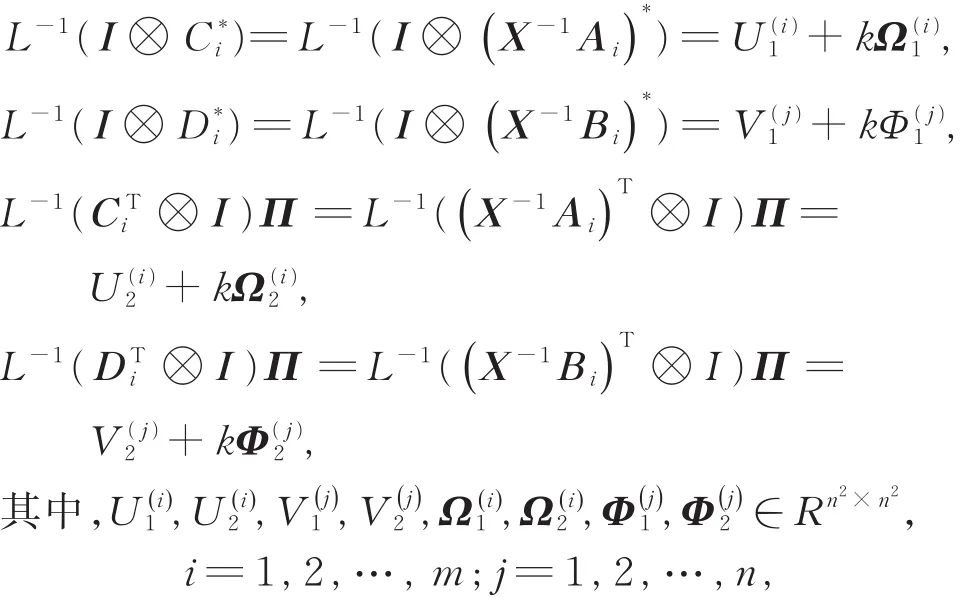
Π为向量置换矩阵，使得vec(KT)= Πvec(K)。

对i=1,2,…,m;j=1,2,…,n，记

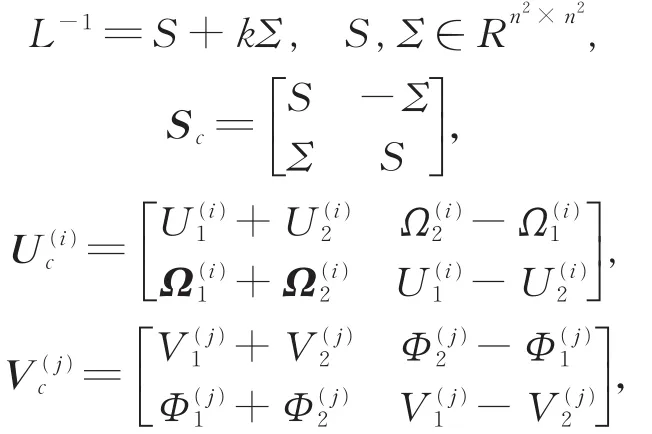
则可得

定理3令则由式（10）定义的条件数可表示为其中，

K=(ρ Sc,μ1Uc(1),...,μmUc(m),η1Vc(1),...,ηnVcnS,,,i=1,2,…,m;j=1,2,…,n如c前定义。

注1由式（11），可得相对条件数为

其中，

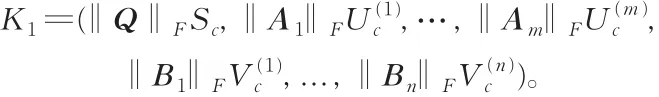
情形2实数域情形

若方程（1）所有的系数矩阵A1,A2,...,Am,B1,B2,...,Bn,Q都是实矩阵，则其唯一正定解也是实矩阵。此时，类似于定理3，有

定理4令A1,A2,…,Am,B1,B2,…,Bn,Q都是实矩阵，设

则由式（11）定义的条件数可表示为

其中，

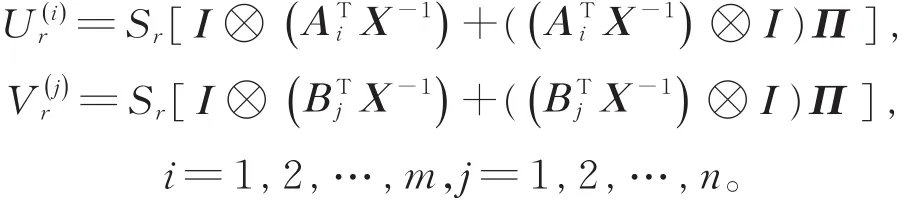
注2 由式（13），可得相对条件数为

其中，J1=(‖Q‖FSr, ‖A1‖F,...,‖Am‖F,‖F, …, ‖Bn‖F)。

4 数值例子

本节利用数值实例来说明理论结果。程序采用 Matlab 7.1语言，机器精度为10-16。迭代结束条件为

例1 令m=n=2，考虑矩阵方程（1）的正定解。矩阵A1,A2,B1,B2,Q如下：

计算可得

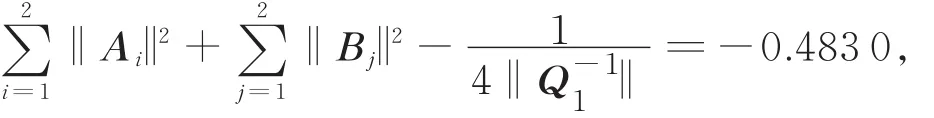
由定理1，利用迭代式（2），迭代17步后可得矩阵方程（1）的唯一正定解

误差为

误差为

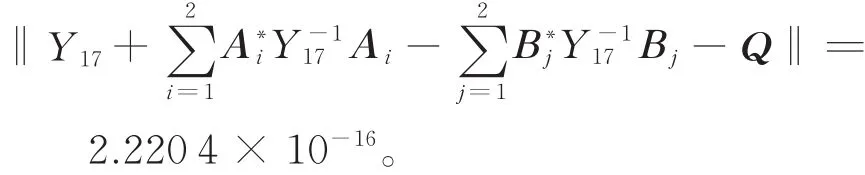
例2 令m=n=1，考虑矩阵方程X+A∗X-1A-B∗X-1B=Q 及扰动方程͂+͂-1͂-∗-1͂=͂，其中，

经计算，

由定理1迭代18次后得到唯一正定解：

此时误差为

进一步，不难验证对每个j=3,4,…,7,扰动后矩阵方程͂+͂-1͂-͂∗͂-1͂=͂满足定理2的所有假设，故分别有唯一正定解X͂，且可分别由迭代（2）得到。此外，记 ΔX=X͂-X，可分别通过式（5）得到‖ΔX‖的上界估计，具体数值见表1。

表1 X的扰动估计Table 1 Perturbation bound of X

例3 考虑矩阵方程（1）的唯一正定解的Rice条件数，其中 m=1,n=2，a1=0.025+10-k，

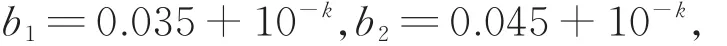
由式（14）得，当k取不同值时的Crel(X) 见表2，可见此例中唯一正定解是良态的。

表2 不同值下的Rice条件数Table 2 Rice condition number for different k

5 结 论