基于共轭梯度法的感知矩阵优化方法

李昕艺，刘三阳，谢维，

（西安电子科技大学 数学与统计学院，陕西西安710126）

压 缩 感 知 理 论（compressivesensing）由DONOHO等于2006年提出，可以从低维压缩信号中高概率恢复原始高维信号［1-2］。应用压缩感知理论可降低信号的采样和传输成本，是一种非常适合信息爆炸时代的信号采样和处理理论。

压缩感知理论包括信号的稀疏表示、观测信号采集、信号重构三部分。观测信号采集是压缩感知理论降低信号采集率的关键步骤，通过观测矩阵的线性变换将高维信号投影为低维信号，公式为

其中，y∈ RM×1为观测信号，x∈ RN×1为原始信号。由于M≪N，该过程能显著降低信号维数，为信号的存储、传输提供便利。如何构造有效的测量矩阵是观测信号是否包含原信号全部信息的关键。

自压缩感知理论问世以来，测量矩阵主要可分为随机测量矩阵和确定性测量矩阵两大类。随机测量矩阵主要包括高斯随机矩阵［3］、伯努利随机矩阵［4］、部分傅里叶矩阵［5］等。这些矩阵均能在一定概率上重构原始信号，但因随机数的生成和存储对硬件要求较高，往往难以实现。

由于随机性测量矩阵在实际应用中存在难以克服的缺点，确定性测量矩阵在压缩感知理论中的应用尤为重要。从构造原理出发，确定性测量矩阵可分为4类：（1）基于有限域的测量矩阵［6］。从特定有效域出发，构造满足限制等容性［2］的测量矩阵；（2）基于编码的测量矩阵［7］。针对特定的编码构造满足指定性质的测量矩阵；（3）基于训练的测量矩阵［8-9］。将随机矩阵作为初始矩阵，结合稀疏基，不断优化，使得感知矩阵逼近ETF［10］框架的测量矩阵；（4）最大 Welch界等式测量矩阵［11］。利用数值搜索方向构造最大Welch界等式测量矩阵。

本文基于共轭梯度法的感知矩阵优化方法不同于常用的优化测量矩阵方法，属于确定性测量矩阵中的第3类构造方法。在EFT框架的基础上，通过优化感知矩阵，并利用共轭梯度法生成下降方向，可实现加速下降，简化梯度计算。仿真实验表明，本方法在理论分析、实际图像应用及算法有效性方面均优于其他方法。

1 预备知识

1.1 压缩感知理论

由压缩感知理论，信号y可稀疏表示为

其中，y∈RM×1为观测信号；Φ∈RM×N为投影矩阵；Ψ∈RN×L为稀疏基；α∈RL×1为稀疏信号。这里D=ΦΨ为感知矩阵，需满足限制等容性要求［2］。由于M≪N，可实现信号压缩与采样同时进行，大幅度减少采样量，从而减小数据的传输压力。

信号x可应用于压缩感知理论的前提是该信号能被稀疏表示，即

若‖α ‖0=k(k ≪N)，则称 α 为k-稀疏信号，x为可k-稀疏化的。

将压缩感知理论应用于实际，需从观测信号y中重构原始信号，称之为信号的重构过程。该过程的原始模型为

由于该模型为非凸的欠定方程求解模型，有研究表明其等价于凸模型［12］：

由于l1范数是凸的，这样就将一个非凸优化问题转化为凸优化问题，方便求解。

1.2 观测矩阵构造

从测量信号y中重构出精确唯一的原始信号x的［13］必要条件为感知矩阵D= ΦΨ ∈ RM×L满足[13]：

其中，spark(D)为D中线性相关的列的最小数目；K为x的稀疏度。显然spark(D)越大，对信号稀疏度的要求越低，信号重构效果越好，但直接求解关于spark(D )的最大化问题十分困难。由文献［13］知，当时，x也能被完美重构，μ()D为D的相互关系数，定义为

其中{di}为D的列。文献［14］给出了D的相互关系数的界限：

基于此，可利用D的Gram矩阵G=DTD来设计目标函数，其展开式为

G的非对角元素越接近0越好，故要求G接近对角矩阵，当然其非对角元素不可能为0。对G做归一化处理 ，将其对角元素化为 1，即=ˉ，其中=DxDx，D=diag(… ,,… )。此时，显然有对 ∀i，有‖=1,则2的相互关系数为

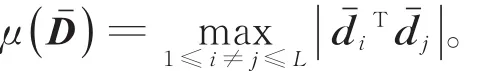
文献［10］首次提出用ETF框架来解决观测矩阵的构造问题，该框架要求归一化的Gram矩阵Gˉ接近一个目标对角矩阵Gt，其中Gt从δeft中选择：

常数ξ＞0，可限制搜索空间以找到合适的目标矩阵。

利用感知矩阵D的Gram矩阵在ETF框架下迭代产生感知矩阵来构造测量矩阵。目标函数为

考虑到ETF框架需要对D进行归一化处理，文献［15］提出了利用μˉ)测量矩阵的构造方法：

2 感知矩阵优化方法

在文献［15］的基础上，引入共轭梯度来简化梯度计算，同时观察到在稀疏基Ψ已确定的情况下，观测矩阵构造过程和稀疏信号恢复过程中，用到的都是感知矩阵D而非观测矩阵Φ。因此，本文设计了基于感知矩阵D的梯度的共轭梯度求解算法。模型为

由于该模型有2个变量D和Gt，因此，采用交替更新的方法分别求解。在固定Gt的情况下，采用共轭梯度法更新感知矩阵D；接着固定D，利用收缩算子更新目标Gram矩阵Gt。

2.1 共轭梯度法更新感知矩阵

记E=Gt-，则感知矩阵优化模型可改写为

对D求导，有

其中dij是D中第( )i,j个元素，又有

又

其中εmn为E的第(m,n)个元素，注意到=1，则上式可改写为

整理得

文献［15］中的梯度计算公式为

其中，Γ为对角矩阵，其对角元素与Q的对角元素相同，

与其相比，本文所设计的目标函数关于D的导函数少了一个矩阵乘法运算，更为简单。

同时，为减少迭代次数，采用共轭梯度方法进行更新，直至得到最优的感知矩阵D：

其中，λ为步长，V(k)为搜索方向。步长λk为序列{δj,j=1,2,… }中使函数值下降的最大值，其中δ ∈(0 ,1 )［16］。搜索方向 V(k)的更新方式如下：

其中因子βk的计算方法由文献［17］给出：

2.2 收缩算子更新目标矩阵

用文献［10］的方法来更新目标Gram矩阵Gt：

其中，ζ=G(k-1)(i , j)，ξ为ETF框架中限制搜索空间的参数。

固定稀疏基Ψ，给定初始测量矩阵Φ0，可得初始感知矩阵D0=ΨΦ0。本文所设计的基于共轭梯度法的感知矩阵D的优化方法如下：

Algorithm 1感知矩阵优化方法

输入初始感知矩阵D0，初始下降方向d0，参数δ=0.5，迭代步数ite；

输出最优感知矩阵Dopt；

步骤1更新目标Gram矩阵Gtk；

步骤2计算归一化感知矩阵Dˉk=DkDxk，并计算 Gˉk=DˉTDˉ；

步骤3计算梯度，计算因子 βk；

步骤4更新方向：βkV(k-1)a；

步骤5更新步长：选择λk为序列{δj，j=1，2，…}中使得目标函数值下降的最大值。

步骤6更新感知矩阵：Dk=Dk-1+λV(k)；

步骤7若k＞ ite，则停止，输出Dopt=Dk；否则，置k=k+1，转步骤 1。

3 实验结果

将 ELAD［18］、XU［19］、TIAN［20］及最新的 NSMD方法做对比，从理论分析、真实图片恢复效果和算法效率三方面通过实验验证所提出的感知矩阵构造方法的有效性。实验环境为Matlab R2015b。

3.1 理论结果

由ETF框架可知，优化后的感知矩阵D的Gram矩阵应逼近一个对角矩阵。用D的相互关系数μ及平均相互关系数μav作为评价指标来衡量其Gram矩阵与对角矩阵的相似程度。计算方法如下［18］：

为方便比较，固定稀疏基为离散余弦变换基（DCT基），以上方法都为优化同一个高斯随机测量矩阵，且 固 定 迭 代 步 数 为 100，M=102，N=256，ξ=

图1为未优化的高斯随机感知矩阵和ELAD、XU、TIAN、NSMD及本文方法构造的感知矩阵的Gram矩阵非对角元素值的分布直方图。非对角元素越小，所优化的感知矩阵越好。由图1可知，XU、ELAD和TIAN方法所得的非对角元素的值较大，且不接近0，NSMD及本文方法所得感知矩阵的非对角元素均较小；从平均值来看，本文方法略高于TIAN方法；但是从峰值来看，本文方法远优于ELAD、XU、TIAN方法，略优于NSMD方法。表2显示了各个方法的μ值和μav值。

3.2 实际图像重构效果

图1 非对角元素值直方图Fig.1 Histogram of the off-diagonal entries in the Grams

表1 算法性能比较Table 1 The comparison of algorithm performance

从图1和表1中可以看出，本文方法显著优于XU、ELAD、TIAN方法，略优于NSMD方法。为进一步观测所构造的感知矩阵在实际应用中的优势，将各方法应用于实际图像（标准Lena图，大小256×256）重构中，观察实验效果。

实验采用的字典矩阵由K-SVD算法［21］训练所得；重构算法为OMP算法［22］，重构过程的迭代步骤均为20。ELAD、XU、TIAN、NSMD及本文方法的迭代步数均为 100，M=102，N=256，δ=0.5，ξ=。重构精度由PSNR衡量，由于对图片进行了归一化处理，PSNR计算公式为

为模拟现实情况中数据收集存在噪声的特点，给图片添加不同水平的高斯白噪声，观察各方法对噪声的鲁棒性，如图2所示。

由图2知，当高斯噪声水平为10%时，所有方法均能较好重构，其中ELAD和TIAN方法的效果较好。当添加方差为20%的高斯噪声时，XU、ELAD、TIAN方法产生的重构图较为模糊，而NSMD和本文方法效果良好，且本文方法的PSNR值最高。当添加高斯噪声水平为30%时，XU、ELAD、TIAN方法已不适用，而本文方法重构效果依然良好，PSNR值较高。无论噪声水平如何，在某些图像块中，本文方法得到的图像较其他方法更为平滑。由此可知，本文方法对噪声的鲁棒性较高。

3.3 算法有效性

为观察感知矩阵在不同稀疏度下对稀疏重构的影响，利用人工生成的随机信号来验证本文算法对不同稀疏度信号的测量有效性。选择在理论结果和真实图片重构实验中表现较好的NSMD作为对比算法。重构算法均为OMP算法，重构精度由均方误差（MSE）衡量，MSE越大，重构精度越低。MSE计算公式为

图2 图像重构图Fig.2 Image recovery with different sensing matrix

图3 显示了固定N=80，M=15，信号稀疏度K从2到8变化时，MSE随K变化的情况（结果为重复运行20次的平均值）。可以看出，随着K值的增大，2种方法的重构精度均逐渐降低，但本文方法的重构精度要好于NSMD方法。

4 结 论

设计了一种基于ETF框架的新型感知矩阵构造方法。感知矩阵由最小化其Gram矩阵和目标Gram矩阵之间的距离得到。由于求解感知矩阵的梯度比求解测量矩阵的梯度计算更简单，且压缩感知理论重构原始信号中使用的是感知矩阵而非测量矩阵，本文设计了一种基于共轭梯度法的感知矩阵优化算法：在迭代过程中交替更新目标Gram矩阵和感知矩阵，利用收缩算子更新目标Gram矩阵，利用共轭梯度算法更新感知矩阵，并且将感知矩阵的Gram矩阵归一化过程封装在算法内部。该算法不同于常用的基于测量矩形梯度的求解算法。试验结果表明，本文算法在理论分析、实际图像应用及算法有效性方面均具优势。

图3 MSE随稀疏度变化图Fig.3 Mean square error versus signal sparsity