结合光流法与信息熵的人群突发事件检测与判断

邓立，沈继忠，高鹏辉

（浙江大学信息与电子工程学院,浙江杭州310027）

随着经济的发展，监控摄像头应用越来越多，据调查，目前上海的摄像头数量达100万，分布密度为158个·km－2，北京的摄像头数量达115万，分布密度为71个·km－2，这些摄像头给城市安防提供了保障［1］。当然，由于监控设备数量较多，安保人员很难长时间高度关注每一个监控视频画面。为了实时监测视频并对突发事件报警，智能监控技术应运而生［2-3］。

智能监控技术在实时观测被监控场景时，能自动对视频中的运动目标进行提取、跟踪和检测［4-5］，并实现对运动行为的描述和分析，如果检测到异常行为就发出警报，为保护人身和财产安全提供帮助。

群体行为往往会导致严重的安全事件，因此在安防领域，更需关注群体行为的检测。目前，对人群突发事件的检测有提取运动特征进行判断［6-7］、基于社会力模型分类［8-9］、通过信息熵表示人群分布信息［10-13］等，文献［11］计算了视频中每个像素点的行为熵，通过场景行为熵检测人群异常行为；文献［12］论证了在人群混乱状态，信息熵会很高，在人群有序状态，信息熵会很低；文献［13］结合人群状态指数、人群运动强度指数、人群混乱指数分析人群状态。现有研究主要通过速度与熵检测人群状态，速度反映当前的运动状态而非运动状态的变化，加速度才能更好地反映突发事件发生时人群运动状态的变化。目前，人群异常检测是综合人群密度、运动状态、人群混乱度等信息来判断的。人群速度突变和混乱程度增加均属异常，现有研究缺乏对人群异常的细分。人群突发事件是指由于自然或人为原因使人群的运动状态发生改变，人群突发事件分为有序和混乱两类。有序的突发事件是指尽管加速度很大，但人群向着同一方向有序地撤退；混乱的突发事件是指加速度很大，人群四散而逃，向多个方向运动。

本文针对视频监控中的人群突发事件检测和判断进行研究，提出了光流法与信息熵相结合的一种检测算法，此算法能准确检测突发事件并判断人群状态，适用于多种不同背景的环境。通过LK光流算法提取视频中运动物体的特征点［14-15］，得到运动物体特征点的位置、速度和加速度信息，分析运动强度，检测突发事件。通过计算各速度矢量的概率分布，得到信息熵，表征视频中的混乱度，从而判断视频中人群的混乱情况，对事件做出判断。

1 人群突发事件检测算法

1.1 Lucas-Kanade光流算法

光流是基于像素点定义的，是一种图像运动的表达方式。当观察者与被观察物体发生相对运动时，物体的像素点在成像平面上运动，好像是一种光的“流”［16-18］。实际上光流［19-20］是运动物体在二维图像平面上的投影，光流的集合称为光流场［21-22］。

LK光流算法［23］有以下3个假设条件［24］：

（1）亮度恒定：在视频相邻帧之间，运动目标的亮度保持不变；

（2）时间连续：时间发生变化很小时，帧间对应的运动目标像素点的运动也足够小；

（3）空间一致性：相邻的像素点具有相似的运动。

通过光流法的3个假设可以得到光流值与灰度值的关系矩阵：

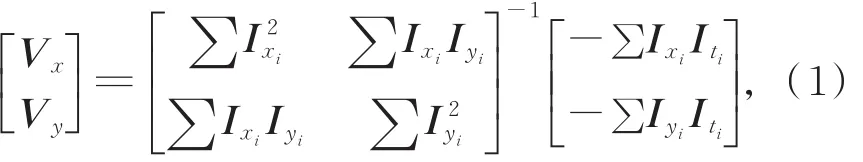
I(x,y)是图像上像素点(x,y)处的灰度值，i是视频帧数。Vx与Vy即为像素点在x与y方向上的光流。由式（1），可求出每一像素点对应的光流值。

LK光流法用于提取和跟踪特征点，是本文检测算法的基础。

1.2 信息熵的概念

香农将统计物理中熵的概念引进了信息论，是现代信息论的创始人［25］。在信息论中，熵用来衡量系统的无序程度。一个系统信息熵H的大小与该系统的状态概率p有关，概率p越小，系统所包含的信息熵H越大［26］。信息熵还可用来度量变量间的相关度，对大型数据集的相关性分析非常重要［27］。如果一个系统由状态集{a1,a2,…,an}组成，而每一个状态所对应的概率分别为p1,p2,…,pn，，那么系统的信息熵H定义为

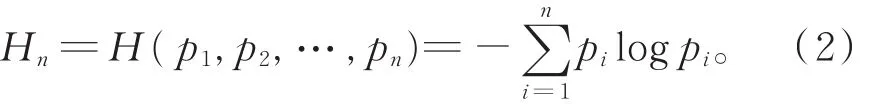
信息熵具有以下基本性质［28］：

（1）最大信息熵：Hn=H(p1,p2,…,pn)≤ logn，当且仅当,i=1,2,…,n时取等号。

（2）最小信息熵：Hn=H(p1,p2,…,pn)≥ 0，Hn=0当且仅当pi=1,p1=p2=…=pi-1=pi+1=…=pn=0。

（3）对称性：H(p1,p2,…,pn)=H(p2,p1,…,pn)，即样本重新排序后，熵保持不变。

从以上信息熵的性质可以看出，若用信息熵来描述一个系统的运动状态，当系统中运动状态趋向一致时，会出现最小的熵值，此时系统是有序的；反之，当系统中各个运动状态都不同时，会出现最大的熵值，此时各个方向的运动状态出现的概率相等。

信息熵代表了混乱度，是算法的关键。将信息熵应用于突发事件检测，可方便判断人群处于混乱还是有序状态。

1.3 人群突发事件检测步骤

突发事件发生时，人群的运动强度会发生很大的变化，特征点的加速度相对较大；如果人群处于混乱状态，那么，计算得到的所有特征点的信息熵会很大。为此，提出检测突发事件、判断人群混乱状态的算法步骤：

（1）光流法提取并追踪视频中图像的特征点；

（2）根据每帧图像中特征点的位置变化，计算其运动加速度，通过设定加速度阈值分析特征点的运动强度，检测是否有突发事件发生；

（3）将速度矢量方向划分为8个区域，计算特征点的速度矢量在每个区域中的分布概率pi；

（4）根据式（2）由分布概率pi计算信息熵，通过信息熵的大小，判断事件中人群状态是有序还是无序。结合运动强度与混乱度检测并判断突发事件的紧急程度。

各步骤具体描述如下：

步骤1调用goodFeaturesToTrack函数获得图像中的特征点，通过光流算法得到特征点(x,y)在视频的第t帧对应的位置信息(Vx,Vy)。

步骤2通过位置信息计算速度，公式为

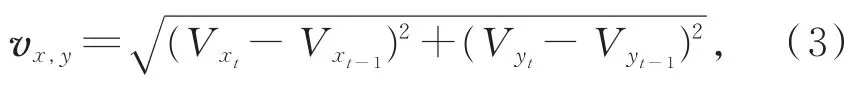
前一帧和后一帧的速度差即为加速度。

假设其中共有n个特征点，特征点对应的光流加速度分别为a1,a2,…,an，对光流加速度进行高斯滤波处理，抑制异常的光流加速度，得到高斯滤波后的第m个光流加速度：

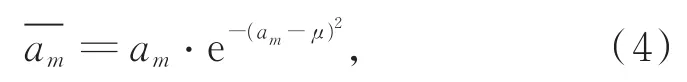
加速度阈值的设置方法：检测一个突发事件未发生的场景，获取一段时间内的视频，并输出视频图像中特征点的加速度数据，加速度阈值设定为加速度数据中最大值的2倍左右，加速度阈值与场景、光照、人群密度等有关。在此基础上可通过信息熵的大小判断人群状态是有序还是混乱，从而判断是否易发生安全性事故。

步骤3如图1所示，将速度矢量方向划分为8个区域，统计各速度矢量在每个区域的分布数量，各区域速度矢量的数量除以速度矢量的总数得到速度矢量在方向上的分布概率pi。本文用分布的统计结果近似代替概率。

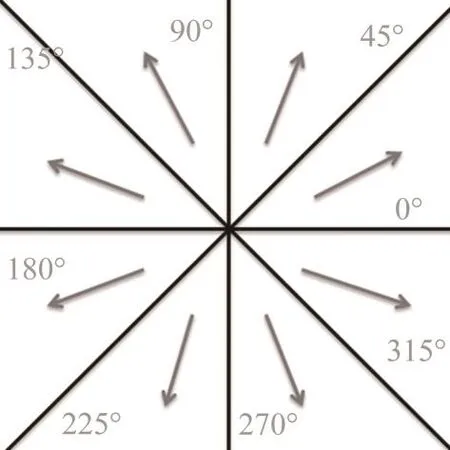
图1 信息熵计算分区示意图Fig.1 Partition diagram for information entropy calculation

步骤4根据式（2）的定义计算信息熵Hn。计算时以10为底取对数，Hn的单位为det（迪特），根据实验测试设置信息熵的阈值为0.5 det，当信息熵超过阈值时，人群处于混乱状态，否则，人群处于有序状态。根据信息熵的性质，最大熵为lg 8=0.903 det，最小熵为0。测试验证得到，阈值设置为0.5 det就可很好地区分混乱和有序状态。值得注意的是，本文是对运动矢量统计计算得到信息熵，而非计算静态像素分布熵，反映的是视频中人群的运动情况。

2 实验结果与分析

分析了研究者自己拍摄的人群突发事件视频、UMN（University of Minnesota）数 据 集［29］视 频 和PETS 2009［30］数据集视频。

2.1 自拍摄人群突发事件视频

突发事件发生前人群的行为有自由行走、定向行走、人群静止等，一共有6段视频，分辨率为640×480，帧率为 30 fps。

按照1.3节中的检测步骤，计算视频中的加速度和信息熵，图2（a）显示了人群突发事件视频的截图，图2（b）显示的是加速度随帧数变化的检测结果，根据1.3节中的阈值设置方法，加速度阈值设置为100，加速度的单位是像素/帧2。可以看出，在视频的0～184帧中，加速度在阈值内，未发生人群突发事件。184～218帧，加速度超过阈值，检测到有突发事件发生。图2（c）显示的是加速度超过阈值时信息熵的大小，可以看出，在加速度大于100时，对应时间范围内信息熵均大于阈值0.5 det，说明视频中的人群处于混乱状态。将算法检测的结果与视频的真实情况进行对比，两者情况相符。当视频中加速度超过阈值时，判断人群是否处于混乱状态，结合运动强度与混乱度判断突发事件的紧急程度，并判断是否易发安全性事故。

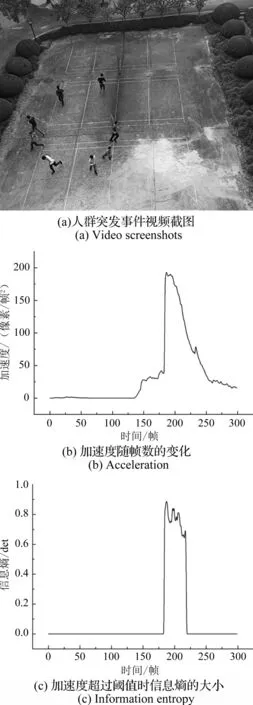
图2 自拍摄视频测试结果Fig.2 Test results of our video

本文没有将加速度小于阈值的信息熵输出，是因为未发生突发事件检测人群的状态无太大意义。例如，人群随意走动时，混乱度也很大，但不会发生安全事故。而且，减少不必要的计算可以提高算法效率。

突发事件发生后人群处于有序状态的视频检测结果如图3所示。

2.2 PETS 2009数据集

PETS 2009数据集的S3部分是人群事件识别的内容，包括4种不同的户外背景，分辨率为768×576。

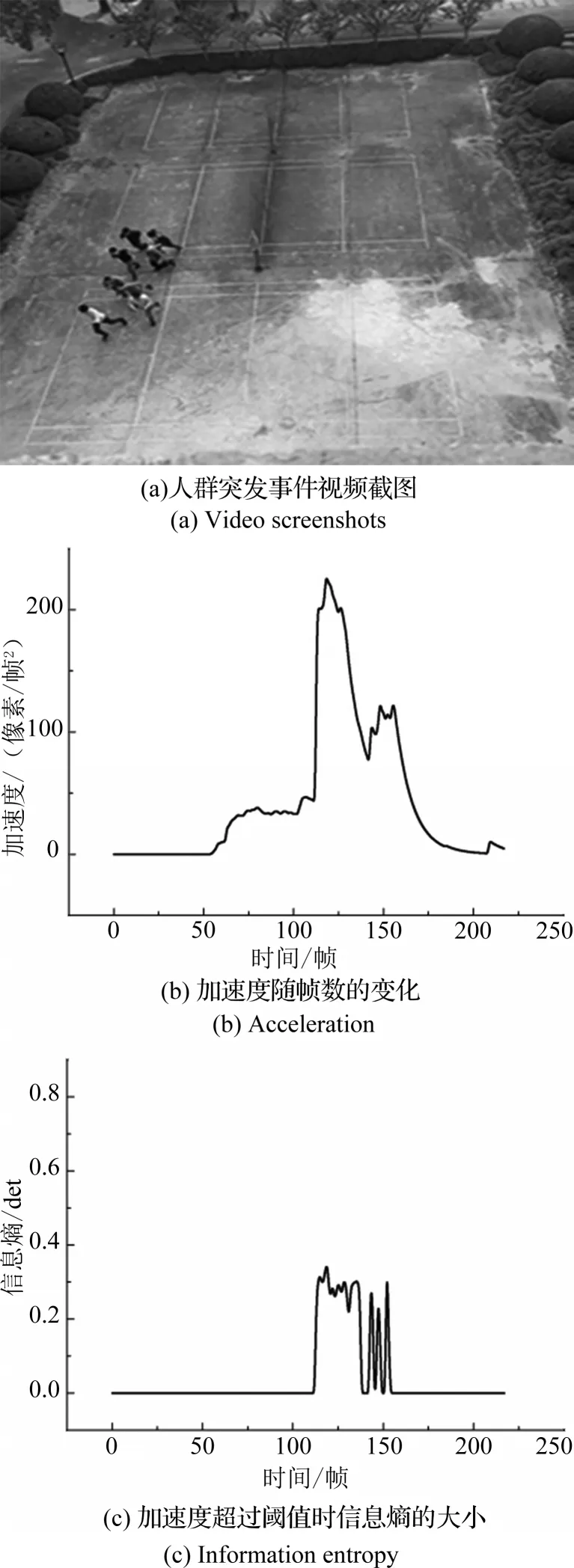
图3 自拍摄视频测试结果Fig.3 Test results of our video

图4 显示了PETS 2009数据集的测试结果，从图4（b）中可以看出，算法有效地检测出了人群突发事件，结合图 4（a）和（c）发现，第 1段和第 2段视频人群处于有序状态，第2段和第4段视频人群处于混乱状态。检测结果表明，算法能有效检测出突发事件，并判断人群处于混乱还是有序状态。

2.3 UMN数据集

UMN数据集中人群异常行为检测的部分包括公园草地、广场、室内走道3种背景的11个视频片段，分辨率为320×240。

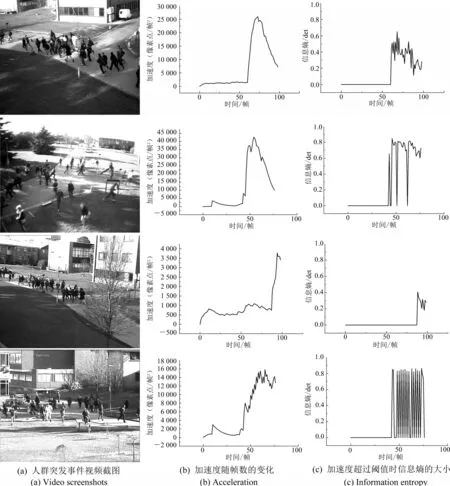
图4 PETS2009数据集测试结果Fig.4 Test results of PETS 2009 Dataset

图5 显示了UMN数据集的测试结果，从图5（b）中可以看出，算法有效检测出了人群突发事件，结合图5（a）和（c）可以发现，第1段和第2段视频人群处于混乱状态，第3段视频人群处于有序状态，检测结果与实际情况相符。

2.4 实验结果分析

2.4.1 对比图3～图5中不同背景视频的检测结果发现，在排球场、公园草地、广场、室内走道等背景中，算法能有效检测突发事件，判断人群状态。实验采用多种场景，这些场景的光照、对比度、色彩等各不相同，说明算法适用范围广。

2.4.2 实验结果对比显示，算法根据信息熵的大小判断人群的状态，有效区分人群处于混乱还是有序的状态，可为突发事件的紧急程度判断提供参考，从而有针对性地采取措施。

2.4.3 图3属于局部事件，即发生突发事件的人群只占整个画面的一部分；图5属于全局事件，发生突发事件的人群几乎占据了整个画面。从局部事件和全局事件的测试结果看，无论视频中人群的像素点占画面的小部分还是大部分，对算法均无影响，均能有效检测出突发事件，判断人群处于混乱还是有序状态。

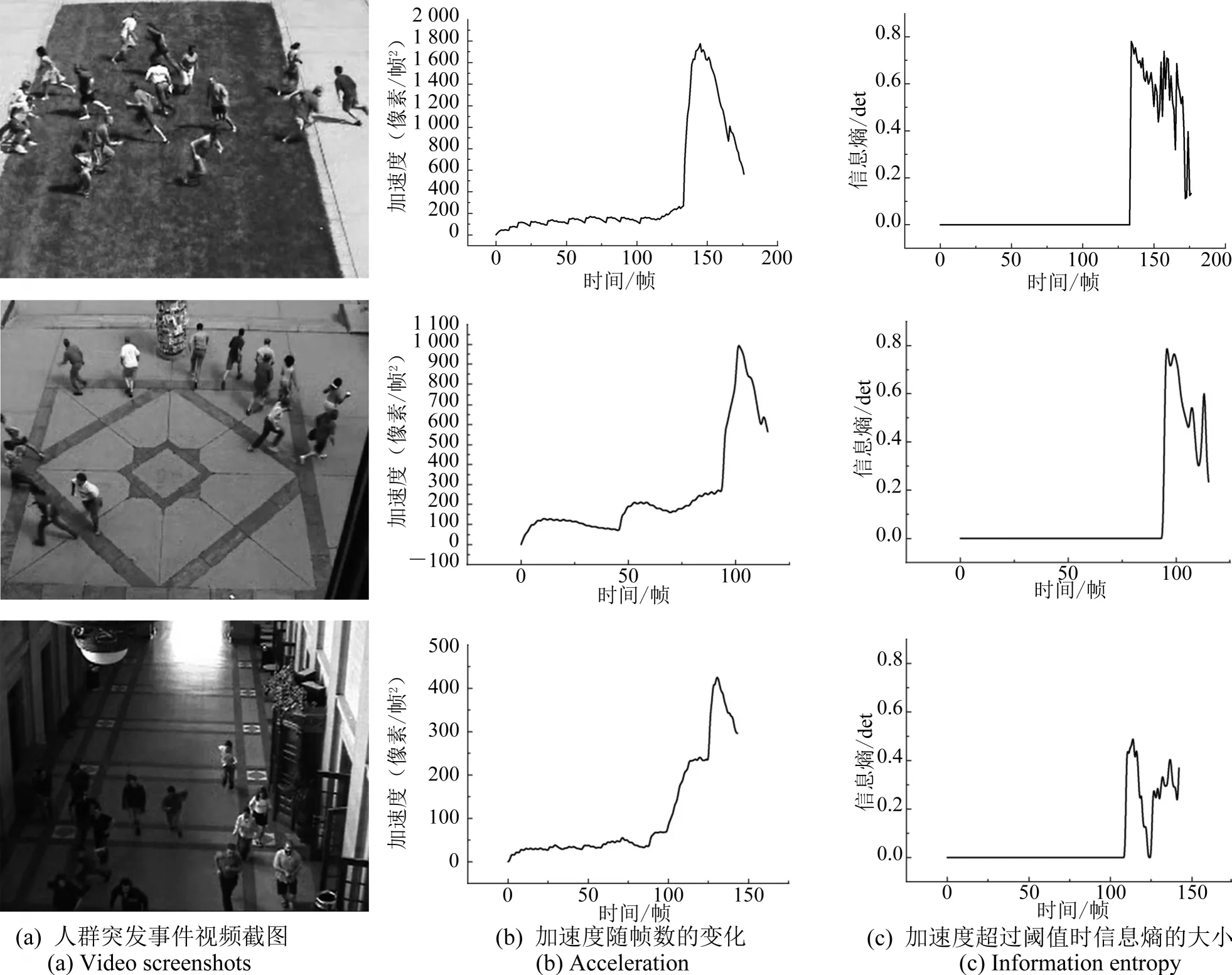
图5 UMN数据集测试结果Fig.5 Test results of UMN dataset

2.4.4 目前视频监控中常用的分辨率为QCIF（176×144）、CIF（352×288）、HALF D1（704×288）、D1（704×576）等［31-32］，测试数据集中分辨率为320×240,640×480，768×576，本方法仍能准确检测人群突发事件。

2.5 同类人群突发事件检测算法比较

国际上通常使用受试者工作特征曲线（receiver operating characteristic，ROC）反映人群突发事件检测算法的准确性和鲁棒性，本文算法的ROC曲线如图6所示。

定义ROC曲线与x轴和直线x=1围成的封闭区域面积为 AUC（area under the curve），AUC值越大，检测算法的准确性和鲁棒性越好［33］。

在众多人群异常事件检测算法的文献中，将UMN数据集［29］作为测试集，本文基于UMN数据集对不同算法的性能做对比。性能比较好的为KALTSA 等［7］结 合 histograms of oriented swarms（HOS）和 histograms of oriented gradients（HOG）进行检测的工作，以及MARSDEN等［6］通过人群聚集和冲突的特征（holistic features）检测突发事件的工作，表1为本文算法与这2种算法基于相同的UMN场景的结果。

从表1看，以上3种算法都具有较高的性能，本文算法较文献［6］算法的准确性和鲁棒性更高，较文献［7］算法性能稍逊，但费时较文献［7］少很多，在158×238分辨率下，文献［7］算法的时间是0.91 s/帧，本算法在320×240分辨率下的时间为0.03 s/帧，并且本文算法能在准确率较高的基础上区分突发事件中人群的混乱或有序状态，对事件的紧急程度做出判断。

综上所述，结合光流法与信息熵的人群突发事件检测与判断算法可有效检测突发事件，判断人群处于混乱还是有序的状态，有助于更好地获得视频中的信息。实验结果表明，该算法适用于多种不同背景的环境，适用范围广；多次实验结果与实际相符合，准确率高。

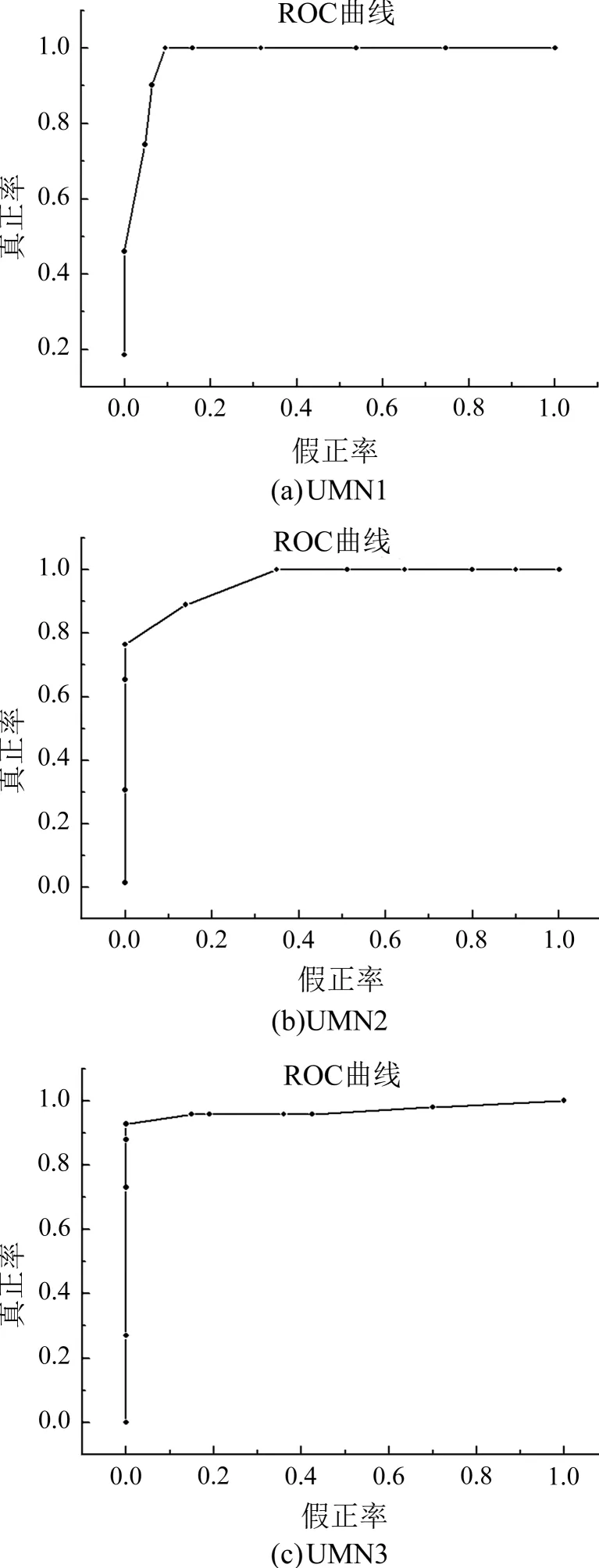
图6 UMN测试集的ROC曲线Fig.6 ROC of UMN dataset

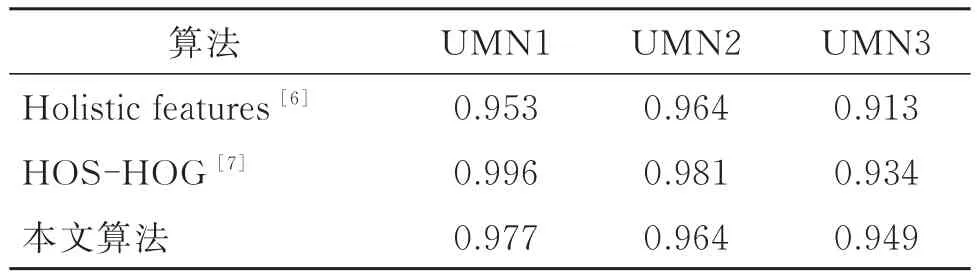
表1 不同算法AUC比较Table 1 Comparison of different algorithms

3 结 论

提出了一种结合光流法与信息熵的人群突发事件检测与判断算法。该算法将信息熵的概念与智能视频监控相结合，表征了视频中人群的混乱度。通过LK光流算法从视频中提取运动物体的特征点，得到其位置信息，由位置信息计算速度和加速度，分析运动强度，检测突发事件；根据各速度矢量的概率分布计算信息熵，由此来判断视频中的人群是混乱还是有序。与同类研究相比，因本研究将加速度与信息熵相结合来检测突发事件、判断人群状态，能更好地反映突发事件发生时人群运动状态的变化，对人群状态是混乱还是有序做了细分，有利于判断突发事件的紧急程度，从而合理配置救援资源。本算法在测试视频中AUC值平均达到0.963，当视频分辨率为 320×240、640×480、768×576时均有较高的准确性和鲁棒性。