一种基于改进Bhattacharyya距离的高斯网络协方差矩阵灵敏度分析方法

朱明敏，刘三阳

（西安电子科技大学 数学与统计学院，陕西西安710126）

随着科技、计算机技术和互联网技术的不断发展，数据量爆炸式增长。由于数据获取方式的随机性和复杂性，以及人类认识的不完全、不精确和不一致性，使得数据模式之间的关系极其复杂，存在大量的不确定性。研究不确定性问题的知识表示、推理和学习方法，从目标数据中提取潜在的可利用信息，对决策过程进行辅助支持，成了亟待解决的问题［1-4］。图模型作为概率统计与图论相结合的产物，因其较好的灵活性、简洁性以及成熟的理论，在不确定性知识的表达和推理方面具有独特优势，已成功应用于机器学习、人工智能、生物信息学、金融分析与预测等领域［5-8］。

高斯贝叶斯网络（Gaussian Bayesian networks，GNs）［5］是一种特殊的图模型，由定性和定量两部分组成，定性部分是一个有向无环图（DAG），表示变量之间的依赖结构，定量部分由分配给随机变量的高斯条件密度函数组成。从所给数据集中确定GN的结构和参数等价于估计多元正态分布的均值向量和协方差矩阵。协方差矩阵的估计往往非常困难。首先，作为估计的矩阵正定性很难保证，其次，待估参数的个数随矩阵维数成二次方增长，难以保证估计结果的精确性。另一方面，在许多实际问题中，环境变化或外部刺激往往会改变随机变量之间的条件依赖性，并可能在相应的图模型中产生重大的结构变化，导致模型参数（协方差矩阵）发生变化。因此，由数据检测其结构变化并帮助系统适应新的环境非常重要。基于此，为深入分析图结构变化的形式和特点，通常用灵敏度分析方法［9-14］来研究模型的输出如何随其结构或参数的变化而变化，其结果可作为结构或参数调整的依据，同时可用来研究模型输出对参数变化的鲁棒性。

基于以上分析，本文提出一种改进的Bhattacharyya距离［15］用于度量2个协方差矩阵之间的差异性，简称为SΣ距离，证明了该距离在正定矩阵空间中满足距离的3个性质：正定性、对称性以及三角不等性，并将SΣ距离用于GN协方差矩阵的灵敏度分析。数值实验结果表明，利用SΣ距离得到的分析结果与 KL 距离［9，16］、Bhattacharyya距离完全一致，并且由于SΣ距离满足三角不等性，大大降低了矩阵的运算量。

下文内容安排如下：第1节介绍高斯贝叶斯网络及其证据传播的基本概念；第2节给出基于SΣ距离的协方差矩阵灵敏度分析方法；第3节为数值实验；最后为结束语，同时给出了今后的研究方向。

符号约定：在论述高斯网络中的节点或概率分布中的随机变量时，大写字母X、Y、E等表示节点集合或变量集合，带下标的字母或单个字母，如Xi表示单个节点或变量，大写粗体字母X、Y、C等表示矩阵。

1 高斯网络及其证据传播

高斯网络（GN）［5，12］是一个二元组 (G,F)，G 是一个有向无环图，G中的节点与一组有序随机变量{X1,X2,…,Xn}一一对应，G中的有向边反映了变量之间的因果依赖关系；F={f1(x1|pa(x1)),…,fn(xn|pa(xn))}是所有变量的条件概率密度构成的集合。pa(xi)表示第i个变量Xi在G中的父节点集合，显然pa(xi)⊆ {X1,X2,…,Xi-1}(i≥ 2)， pa(x1)=∅。集合F定义了一个关于变量集X={X1,X2,…,Xn}上的多元正态分布N(μ,Σ)：

其中，μ表示n维均值向量，Σ表示n×n正定协方差矩阵。每个变量Xi(i=1,2,…,n)服从以下一元正态分布：

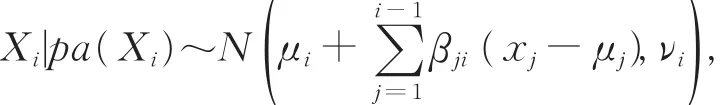
并且满足

其中，μi表示变量 Xi的均值，βji表示变量 Xi关于其父变量 Xj∈ pa(xi)的回归系数，νi表示变量 Xi在给定父变量集下的条件方差。βji实际上给出了Xi和Xj之间的因果依赖强度。若βji=0，那么在G中不存在从 Xj到 Xi的有向边。SHACHTER 等［17］给出了一种通过{νi}和{βji}计算协方差矩阵Σ的公式：

其中，D为对角矩阵，对角元素为条件方差νi，即D=diag({ν1,ν2,…,νn})，B 是以回归系数 βji(j＜i)为元素的严格上三角矩阵。

在实际问题中，当GN的结构和参数确定后，主要任务是计算给定证据变量（取值已知）条件下某些未知变量（或称为目标变量）的后验条件概率分布，这一过程称为证据传播［12］。例如，已知一个证据变量E∈X∖Xi，证据传播结束后，每个变量Xi∈X的后验边缘分布服从正态分布：

其中，μi和 μe分别表示 Xi和 E 的均值，σii和 σee分别表示Xi和E的方差，σie表示Xi和E在证据传播前的协方差。

更一般的情况：若给定一个证据变量集E=X∖Y，证据传播结束后，变量集Y⊂X在E=e条件下服从均值向量为μY|E，方差为ΣY|E的多元正态分布，

2 协方差矩阵灵敏度分析

本节首先给出一种基于Bhattacharyya距离［15］的正定矩阵度量公式，记为SΣ，并证明其在正定矩阵空间中满足距离的3个性质：对称性、正定性以及三角不等性。然后，利用SΣ对高斯网络的协方差矩阵进行灵敏度分析。

2.1 改进的Bhattacharyya距离

假设f1和f2表示参数分别为μ1,Σ1和μ2,Σ2的n元正态密度函数。μ1和μ2分别是均值向量，Σ1和Σ2分别是n×n元正定协方差矩阵，则f1和f2之间的Bhattacharyya距离可通过下式计算：

显然，Bhattacharyya距离满足距离的对称性和正定性，但不满足三角不等性。注意到式（7）右边为2项相加，第1项度量了2个均值向量μ1和μ2之间的差异，第2项给出了Σ1和Σ2之间的差异，且与均值向量 μ1和 μ2相独立。若 Σ1= Σ2，则

若 μ1= μ2，则

注意到式（8）右端取根号即可满足距离度量的3个性质：对称性、正定性、三角不等性。式（9）给出了2个正定协方差矩阵的距离度量，而协方差矩阵属于一类特殊的矩阵空间，即Riemannian流形。式（9）右端取根号，得到关于对称正定矩阵的距离度量：

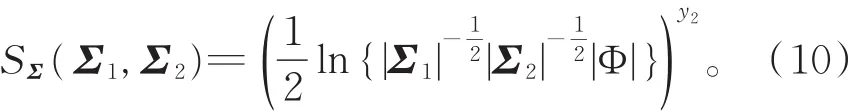
接下来，将证明SΣ(Σ1,Σ2)满足距离度量的3个性质：对称性、正定性以及三角不等性。下面先给出与证明相关的基本概念和引理。

定义1［18］设X非空，φ:X× X↦R是定义在集合X×X上的实值核。φ是正定的当且仅当对∀x,y∈ X，φ(x,y)=φ(y,x)，且对所有n∈ N,

其中{x1,x2,…,xn}⊆ X，{c1,c2,…,cn}⊆ R。

引理1［18］设X非空，φ:X× X↦R是定义在集合X×X上的实值核。φ是负定的当且仅当对所有t＞ 0,exp(-tφ)是正定的。

引理2［18］设φ:X×X→ R是负定的，则存在Hilbert空间H⊆RX和映射φ:X↦H，使得

由以上引理可得到关于SΣ的Minkowski不等式。

定理1设x,y,z∈R且x,y,z＞0。则SΣ满足三角不等式：

若x,y,z∈ Rn且xi,yi,zi＞ 0,i=1,2,…,n，则

证明先证不等式（11）。

若x,y∈ R且x,y＞ 0，则

且

由此可知，

等价于一个Gram矩阵[〈fi,fj〉]，其中

对t＞0,xi＞0是二次可积的。因此，对任意n≥1，G是对称正定的，从而核函数exp(-tφ(x,y))是正定的。故不等式（11）成立。

再证不等式（12）。

若 x,y,z∈ Rn且 xi,yi,zi＞ 0，i=1,2,…,n，则由引理2，存在Hilbert空间H ⊆ Rn和映射φ:X ↦ H，使得

因

此，对p＞ 1，有

因此，

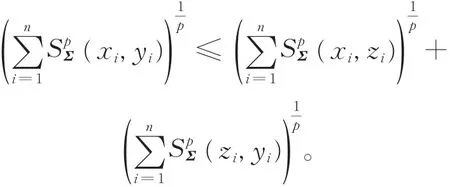
由定理1可证得SΣ(Σ1,Σ2)满足距离度量的3个性质。

定理2设X,Y,Z∈，则

证明由于X,Y,Z∈，所以，存在可逆矩阵 C 使得 CTXC=I,CTYC=D,CTZC=Dˉ，其中D和是对角矩阵，Dii,ˉii,i=1,2,…,n。

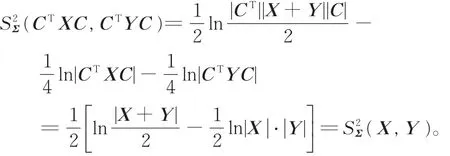
要证明 SΣ(X,Y)≤ SΣ(X,Z)+SΣ(Z,Y)，

只须证 SΣ(I,D)≤ SΣ(I,Dˉ)+SΣ(Dˉ,D)。

易知

由定理1知，当p=2时，不等式

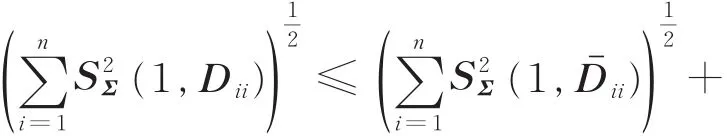
成立。结论得证。

2.2 基于SΣ距离的协方差矩阵灵敏度分析

设μ和Σ表示由统计数据或专家得到的初始模型参数，即X～N(μ,Σ)，其中

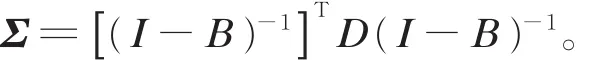
通过对矩阵B和D进行扰动来模拟环境的变化或刺激对初始模型的影响，从而得到扰动后的模型N(μ,ΣΔB

)和N(μ,ΣΔD)，ΔB和ΔD分别表示对矩阵B和D的扰动量，显然ΔB是严格的上三角矩阵，ΔD是对角矩阵。

（1）若对系数矩阵B进行扰动，扰动量为ΔB，则扰动后的模型为N(μ,ΣΔB)，

扰动前后协方差矩阵的距离为

（2）若对矩阵D进行扰动，扰动量为ΔD，则扰动后的模型为N(μ,ΣΔD)，

扰动前后协方差矩阵的距离为

（3）若在模型的扰动过程中同时伴随证据传播，设集合E表示已知证据变量集，Y=XE表示非证据变量集，由式（5）和（6）知，证据传播后的初始模型为N(μY|E,ΣY|E)；对矩阵B和D扰动后进行证据传播，得到扰动后的模型，记为 N(,)和N(,)。其中，

扰动前后协方差矩阵的距离为

注 在证据传播过程中，对协方差矩阵的扰动可能对非证据变量的均值有影响。

3 数值实验

为验证方法的有效性，本文采用文献［12］的GN进行数值实验。该网络用于评估某建筑物钢筋混凝土结构的损坏程度，包含24个高斯变量，27条有向边。其有向图结构如图1所示，有向边上的数值表示变量之间的回归系数，变量X1,X2,…,X16的条件方差为1，其余变量的条件方差为10-4，其参数设置详见文献［12］。

图1 GN有向图结构示例Fig.1 A example of GN

现假设领域专家对模型的定性部分，即网络结构意见不一致，需通过灵敏度分析对网络结构进行调整且要求对原模型的影响尽可能小。由GN的定义可知，系数矩阵B中的元素与有向图中的边是一一对应的，若βji=0，表示在有向图中不存在从Xj到Xi的有向边。因此，可通过矩阵B的扰动来研究图结构的变化。

在钢筋混凝土结构评估问题中，专家们希望找到与原模型最接近又尽可能简洁的图结构。为此，通过每次删除1条有向边后，计算删除前后对应协方差矩阵之间的SΣ距离来判断该有向边对网络结构的影响，表1给出了每删除1条边前后协方差的SΣ距离、KL距离以及Bhattacharyya距离，由表1可知，删除有向边X18→X20对原模型影响较大，删除有向边X16→X24和X15→X24对原模型几乎无影响，得到的SΣ距离与KL距离以及Bhattacharyya距离完全一致。

图2 标准化后的SΣ距离、KL距离以及Bhattacharyya距离对比Fig.2 Performance of the standardSΣKL and Bhattacharyya divergences

图2 给出了标准化后的SΣ距离、KL距离以及Bhattacharyya距离，横坐标表示依次删除的有向边序号，纵坐标表示删除每条边前后对应的协方差矩阵距离。由图2可知，当协方差矩阵之间的差异较小时，SΣ距离对有向边的影响度区分较好；当协方差矩阵之间的差异较大时，KL距离对有向边的影响度区分较好。另一方面，由于SΣ距离满足三角不等性，可直接用来判断多条边的影响度，从而避免了大量的矩阵运算。例如，要判断同时删除有向边X16→ X24和X15→ X24对网络结构的影响，设ŝ表示同时删除这2条边前后的协方差矩阵的SΣ距离，则由表1以及三角不等性知：ŝ≥0.240 370 591-0.10 547 111 且 ŝ≤ 0.240 370 591+0.10 547 111，而利用KL距离和Bhattacharyya距离判断时，无法直接使用三角不等性，需重新计算删除这2条边前后协方差矩阵之间的距离。因此，对于高维复杂问题，利用SΣ距离判断协方差矩阵之间的距离更加有效，可节省大量存储空间和计算时间。

4 结 论

高斯图模型的结构和参数学习是统计学和机器学习领域研究的热点，从所给数据集中确定GN的结构和参数等价于估计多元正态分布的均值向量和协方差矩阵。协方差矩阵的估计往往非常困难，难以保证结果的精确性。因此，常用灵敏度分析方法研究模型的结构和参数变化情况，其结果可作为结构或参数调整的依据，并可用于研究模型输出对参数变化的鲁棒性。本文基于改进的Bhattacharyya距离，提出了一种用于度量正定矩阵差异性的距离公式，证明了此距离在正定矩阵空间中满足距离的3个性质，并将其用于GN协方差矩阵的灵敏度分析。数值实验结果表明，利用此距离得到的分析结果与KL距离、Bhattacharyya距离的结果完全一致，并且由于此距离满足三角不等性，可大大降低矩阵的运算量，适用于高维复杂GN的灵敏度分析。接下来，笔者将进一步考虑将此距离公式应用于图像分类和回归。

表1 删除1条有向边后对应的KL距离、Bhattacharyya距离以及SΣ距离Table 1 The KL，Bhattacharyya andSΣdivergences after removing a directed edge