浅谈立体几何中的创新题
■河南省沈丘县第一高级中学 王 崇 王 超
纵观高考数学试题可以发现,立体几何主要考查考生的空间想象能力、计算及转换能力,以图形的分割、补形、折叠、展开、平移为依托,在图形的变式和非标准图形位置中灵活地运用概念、性质、定理解决相关问题,考查方式灵活多变。
一、立体几何中的截面问题
例1 已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则平面α截此正方体所得截面面积的最大值为( )。
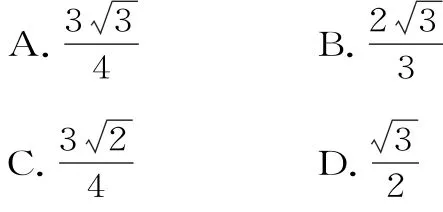
分析:本题主要考查空间直线与平面的位置关系及其所成角的问题,载体为大家最熟悉的正方体,但考查角度较新颖。利用正方体的性质,将每条棱所在直线与平面α所成角转化为共顶点的三条棱所在直线与平面α所成角是解决本题的关键,在此基础上可以利用极限思想和特殊位置的方法解决。
解法1:(直接法)平面A1C1B符合题意,如图1所示。题中的平面α可由平面A1C1B平移得到,如图2所示,六边形EFGHMN即为该截面。
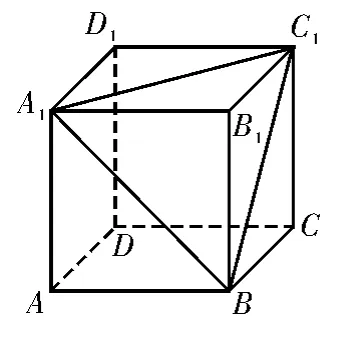
图1
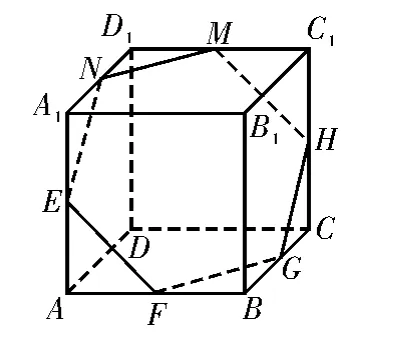
图2
设A1N=x,则有根据对称性可知,延长EN,HM相交于点P,延长EF,HG相交于点Q,如图3所示。由相似比可得,易证∠HEF= ∠EHG=60°,所以△EHQ为等边三角形。同理△EHP也为等边三角形。所以
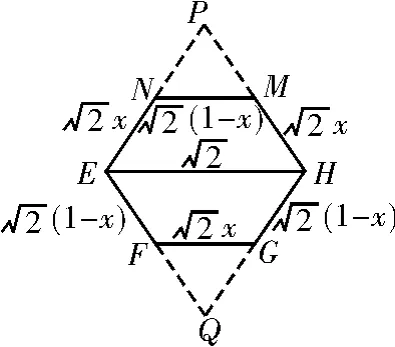
图3
解法2:(特殊位置法)由题可知,截面α应与正方体的体对角线垂直,当平面平移至截面为六边形时,此时六边形的周长恒定不变,所以当截面为正六边形时,面积最大,即
探究本题根源:在人教A版教科书《必修2》“2.2.2平面与平面平行的判定”例2及习题中出现了此题中的面与棱所成角问题,老师当时的讲解稍加延伸考生就会清楚知道截面与正方体各条棱所成的角相等,那么考生有了这样的认识之后再看到这道题时应该很容易找到切入点。
同类题型:
1.能否用一个平面去截一个正方体,使得截面为五边形?进一步,截面能否为正五边形呢?
4.2.4 胶州大白菜品牌发展的不足。胶州大白菜品牌的发展是一个长期的过程,通过建立基地,统一生产、检测等运行机制提高了产品的质量,通过申请商标及各种优秀评选提高了产品的价值,品牌胶州大白菜单位产值、利润率得到提高,品牌发展迅速。但是,胶州大白菜品牌发展过程中仍然存在一些问题,我们需要重视并加以完善。
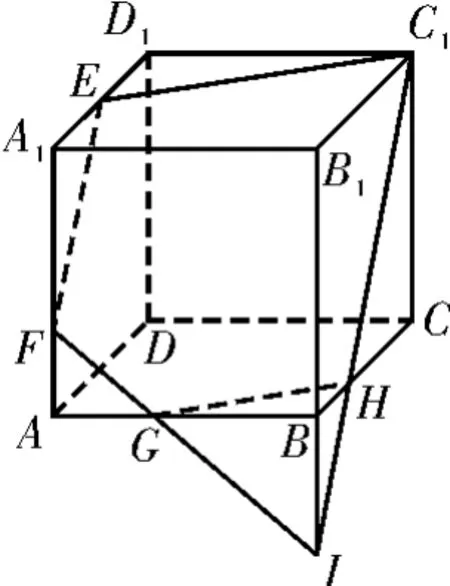
图4
解析:如图4所示,我们可以用一个平面截一个正方体ABCDA1B1C1D1,使得截面为一个凸五边形。I是B1B延长线上一点,使得IB=,E为A1D1的中点,F为AA1上的点,使得,则截面C1EFGH为过直线EF与C1I(这里EF∥C1I)的平面与正方体ABCD-A1B1C1D1相截所得的凸五边形截面。
用一个平面去截一个正方体所得截面不能是一个正五边形。事实上,若截面可以为一个正五边形,则五边形的五条边分属于此正方体的五个不同的面。我们将正方体的每两个相对的面作为一个抽屉,则上述包含正五边形的边的五个面中,必有两个面为相对的平面,它们是平行的,利用平行平面的性质,可知此五边形中有两条边是平行的。但是正五边形的五条边是彼此不平行的,矛盾。
2.正四棱锥P-ABCD的底面是边长为3的正方形,O是P在底面上的射影,PO=6,Q是AC上的一点,过Q且与PA,BD都平行的截面为五边形EFGHL,求该截面面积的最大值。
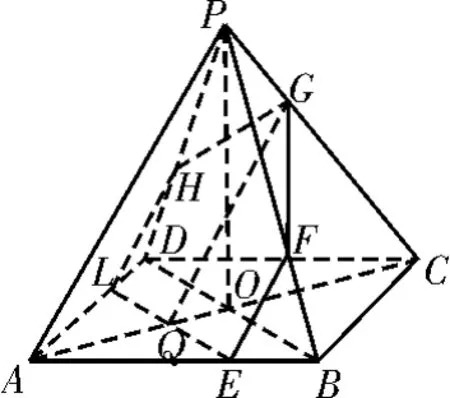
图5
解析:如图5,连接AC,BD,设截面与正四棱锥P-ABCD的底面的交线为EL,AC与EL相交于Q点,由BD∥截面EFGHL得LE∥BD,AP∥截面EFGHL,得AP∥QG,那么,EL必定分别与AB,AD相交于E,L,否则,截面将是三角形,则AP∥EF,AP∥LH,在正四棱锥P-ABCD中,BD⊥AP,由LE∥BD,AP∥QG,知∠GQE是异面直线BD与PA所成角,则QG⊥EL,所以GFEQ和GHLQ是两个全等的直角梯形。
设AE=x(0<x<3),因为AP=,由,即而,由得于是QG=所 以。所以,当x=2时,截面EFGHL的面积取得最大值9。
二、立体几何中的折叠与展开问题
例2 某圆柱的高为2,底面周长为16,其三视图如图6所示。圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在侧视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )。

图6
分析:本题主要考查空间几何体的三视图、直观图及最短路径问题。解决空间几何表面上两点间的最短路径问题的常用方法是把空间图形展为平面图形,利用两点之间线段最短进行求解。
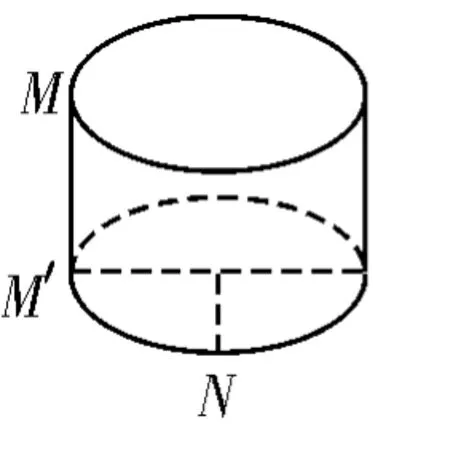
图7
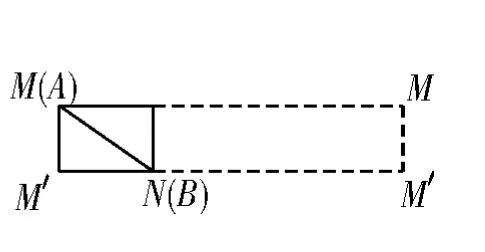
图8
解:三视图还原几何体为一圆柱,如图7,将侧面展开,如图8,则最短路径的长度为M,N连线的距离,所以故选B。
探究本题根源:在人教A版教科书《必修2》第二章小结的回顾与思考中指出“空间图形问题经常转化为平面问题。‘确定平面’是将空间问题转化为平面问题的重要条件,而这种转化又是空间图形中解决部分问题的重要思想方法”。本题既考查了三视图的知识,又考查了空间几何与平面几何的转化问题,解决此类问题常用展开的方法确定相应的平面。
1.如图9所示,一个圆台的上底半径为5,下底半径为10,母线A1A2=20。一只蚂蚁从A1A2的中点M绕圆台侧面转到下底面圆周上的点A2,求:
(1)蚂蚁爬行的最短距离;
(2)蚂蚁在爬行过程中(沿最短距离爬行),蚂蚁与上底面圆周上的点的最短距离。
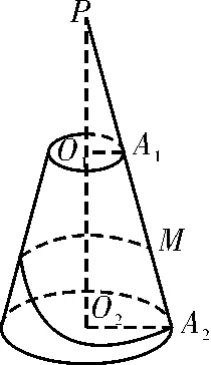
图9
解析:我们将圆台的侧面沿母线A1A2剪开,并展开为一个扇形,如图10所示。设A1A2与A1'A2'的延长线交于点P,利用△PA2O2∽△PA1O1,可知于是故A1P=20。
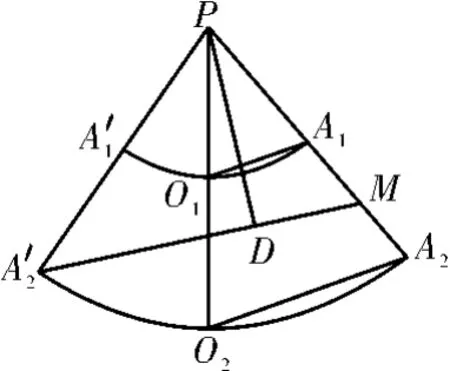
图10
(1)连接A2'M,如果A2'M与扇形A1'PA1没有交点,则线段A2'M的长度即为蚂蚁爬行的最短距离。
利用∠A2'PM为直角,可知A2'M2=A2'P2+PM2=402+302=502,故A2'M=50,这时,我们过P作PD⊥A2'M,D为垂足,则PD=,这表明A2'M与扇形A1'PA1没有交点。所以蚂蚁爬行的最小距离为50。
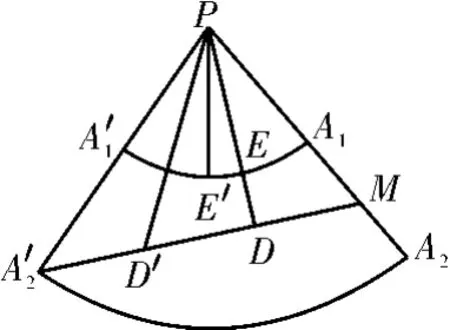
图11
(2)如图 11,设PD交弧A1'A1于点E,我们证明DE的长度即为蚂蚁在沿最短距离爬行时,与上底圆周上的点的最小距离。事实上,设D'E'为所求的最小距离,则PE'+D'E'≥PD'≥PD=PE+ED=PE'+ED,所以D'E'≥ED。这表明,所求的最小距离为ED=4。
三、立体几何中圆柱、圆锥、多面体和球的问题
例3 如图12,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切。记圆柱O1O2的体积为V1,球O的体积为的值是____。
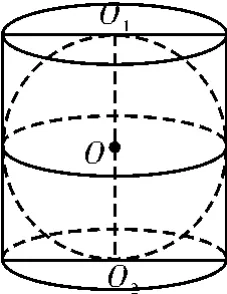
图12
解析:依题意,球O内切于圆柱O1O2,所以圆柱上下底面的半径等于球的半径,可设半径为R,而圆柱的高也等于球的直径。由圆柱体的体积公式得V1=πR2×2R=2 πR3。由球的体积公式得。所以
探究本题根源:在人教A版教科书《必修2》“1.3.2球的体积和表面积”例4中出现了圆柱的内切球和圆柱体积比值的问题,可以把题型延伸到球与多面体、圆锥、圆柱外接和内切的问题。此类题型在高考中多以填空题或选择题的形式出现,解题的关键在于抓住球心到多面体各个顶点的距离都相等,大多是把空间问题转化为平面问题进行解决。
同类题型:
1.在底面半径为2,母线长为2的圆锥内有一个高为1的内接圆柱,则该圆柱的外接球的表面积为____。
解析:圆柱内接于圆锥时,由于对称性,画出过圆锥顶点和底面直径的剖面图,如图13所示,把空间问题转化为平面问题解决。
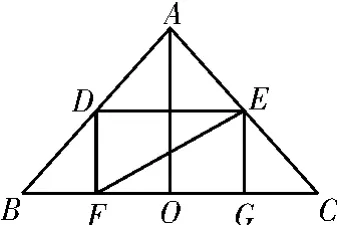
图13

