聚焦观察能力，提升思维品质

田家顺

观察能力是指对客观事物进行认识、分析、发现并抓住典型特征及实质的能力。观察能力是智力结构中的重要组成部分，是人们认识事物、掌握知识、进行思考的基本能力。《数学课程标准》提出：“学生学习数学的过程充满了观察、猜想、实验、验证、推理与交流等丰富多彩的数学活动。观察是获取数学知识的前提，不会观察就不会发现问题，更谈不上解决问题。”那么，小学数学教学中如何培养学生的观察能力呢？笔者从以下几个方面进行了探索。

一、追本溯源，探寻问题的着眼点

米山国藏说过：“在学校学的数学知识，毕业后若没什么机会去用，一两年后，很快就忘掉了。然而，不管他们从事什么工作，唯有深深铭刻在心中的数学的精神、数学的思维方法、研究方法、推理方法和看问题的着眼点等，却随时随地发生作用，使他们终身受益。”小学数学教材中，为了让孩子更好地进行感知，教材提供了大量与学生生活密切相关的材料。教师可以通过这些材料引导学生认真观察，发现事物的细节，注意到常态中呈现出来的不寻常信息，并从中洞悉事物的本质特征，揭示事物与事物之间的联系，从而提高观察的敏锐度。

案例1：“比例的认识”教学片段。

人教版教材中提供了三幅不同大小的国旗，以及国旗的长与宽的数据。

教室前的国旗：长：60cm，宽：40cm。

师：这三幅国旗有什么不同？

生：大小不同。

师：具体指哪些大小不同？

生：长不同，宽不同，面积不同。

师：那有什么是相同的呢？

生：形状相同。

师：形状相同是什么意思？

生：都是一个样子。

师：为什么你们认为这些国旗的形状是相同的？这里面到底有些什么样的数学知识呢？

教师出示每幅国旗长与宽的具体数据，让学生自由猜测，再根据自己的猜想在小组内进行研究，然后汇报。

学生在观察过程中，通常只会进行表层的感知和初步的判断。教师通过有价值的提问，引导学生在观察过程中发现素材中的相同点与不同点，从而迅速找到问题的切入点，提高观察的品质，为思考与解决问题奠定基础。

二、俯视观察，把握事物整体结构

由于人们的阅读习惯是线性的，在感知过程中，孩子的头脑中只会对前后的信息留下印记，而对整体结构缺乏感知。教师提供素材后，可先让学生以自有习惯进行线性阅读，然后有意识地对学生进行提醒，让学生将视线跳出文本，以镜头拉伸的形式，对素材进行全方位的俯视观察，从而对整体进行全面把握。这种观察角度，也有人称为“上帝视角”，有利于学生顺利发现问题，找到其中的规律。

案例2：“一个数除以小数”练习题教学片段。

6÷1.5=1.2÷1.2=49.5÷1.1=

6÷1=1.2÷1=49.5÷1=

6÷0.5=1.2÷0.8=49.5÷0.45=

学生先观察，再互相交流后汇报。

师：你发现了什么？

生1：我发现每一竖排的被除数相同。

师：我们曾经学习过把一竖排叫什么？

生1：列，我发现每列的被除数都是一样的。

生2：我发现第二行除数都是1。

师：还有发现吗？

生3：每列的除数中间都是1，上面比1大，下面比1小。

师：孩子们，在被除数相同，除数比1大或者比1小时可能会是一个什么情况呢？你们能想到吗？

生4：除以比1大的数，商要比被除数小，比如除以2，商就只有被除数的一半。

师：你真厉害，还能自己举例。除数比1小的话，可能会怎样？大家带着疑问，自己做出这些题的答案，看自己的想法是否正確。

……

学者丁祖荫曾研究：高年级儿童具有对事物进行整体感知的能力。在观察活动中，教师要尽量给学生时间，让他们由文本阅读的线性状态转变为整体感知的结构把握状态，把握观察对象的整体结构，确定所观察事物在分类体系中的位置，逐步梳理与概括，得出结论，形成良好的观察习惯。

三、探幽察微，找寻解决问题的办法

数学观察活动是运用已往经验形成的数学直觉，对观察对象进行整理甄别分类的过程。要培养良好的观察能力，需要对事物进行抽象，抽象到能进行区分彼此的相同与不同，从而达到分类研究的目的。

案例3：“鸡兔同笼”教学片段。

按照教材要求，学生在探究环节完成了用列表法解决“鸡兔同笼”问题。学生所列出的表，不仅是完成“鸡兔同笼”问题的结果，也是采用“假设法”解题的研究材料。在第一个研究的结果之上，通过反刍，认真观察研究对象，引导学生区分不同在哪，并思考：如果允许此类情况出现，会现什么结果，怎么解决。

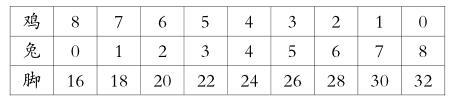
师：同学们，我们刚才通过列表法知道了鸡和兔的具体数量。请大家继续观察我们列出的表，在鸡和兔的数量上，是怎样进行列表的？

生1：鸡和兔的数量是按顺序排列的。师：是按什么顺序排列的？

生1：鸡是从多到少，兔是从少到多。

师：这样做有什么好处？

生1：不会遗漏。

师：不重复不遗漏可以让我们研究问题时非常严谨。我们可以一直排列下去吗？

生2：不可以，因为鸡和兔总共只有8只。

师：是的，这是一个限定条件。那在这8种情况下，你认为有哪些排列不妥当？为什么？

生3：鸡8只、兔0只和鸡0只、兔8只，因为题目说的是有两种动物，而这种情况只有一种动物。

师：嗯，一种情况下只有鸡，另外一种情况下只有兔。现在我们用数学中的假设法来解决这个问题。

……

在培养学生的观察能力时，教师要给学生明确的目标，让他们在纷繁复杂的观察对象中，找到合适的观察范围，避免漫无目的地看。在这个案例中，学生通过观察，对符合数学条件的与符合实际条件的进行区分，从而体悟假设法是把不可能的事进行数学上的设定，寻找引发矛盾的关键点，探究解决问题的方法。

（作者单位：常德市鼎城区永安小学）