与其“面面俱到” 不如“以点带面”——以“双曲线”复习为例

安徽省临泉田家炳实验中学 (邮编：236400)

高三第一轮复习，教师大都追求的是面面俱到，滴水不漏，把每一个“知识细节”覆盖完，这种复习策略高效吗？笔者认为未必.考虑到学生已经学习过一遍，再这样复习会感到乏味，复习效果也会打折扣.与其这样“耗”下去，不如从小处入手，以点带面，直击目标.下面以“双曲线”复习为例，谈谈看法.

1 考情目标

解析几何是高中数学重要内容之一，在高考中占有重要地位.纵观近几年的高考试题，解析几何一般设置两小一大或一小一大，分值大约17～22分.而双曲线作为一种重要的圆锥曲线，是高考的“常客”，尤其是它的两大性质——渐近线与离心率，其命题大都围绕二者展开.相对于椭圆与抛物线，考试大纲对双曲线的要求要低一些，一般是以客观题的形式出现，考查学生的逻辑推理能力和运算求解能力，从中渗透数形结合思想.

2 复习概要

2.1 扎根基础

著名心理学家奥苏贝尔曾说过：“如果我不得不把全部教育心理学还原为一条原理的话，我将会说，影响学习最重要的因素是学生已经知道了什么，根据学生的原有知识状态进行教学.”因此，回顾双曲线的渐近线与离心率，目的是激活学生原有的知识状态，构筑进一步学习的平台，为复习作好准备.尽管双曲线是一种重要的圆锥曲线，是高考的常考知识点，但是笔者仍然抛弃了“大面积撒网”这种费时费力的复习策略，从渐近线与离心率这一小处入手，引领整节内容的复习.

2.2 立足联系

高考命题注重学科的内在联系和知识的综合性，不刻意追求知识的覆盖面.而双曲线的渐近线与离心率之间通过c2=a2+b2建立联系，而明确二者的联系对缩短解题路径，优化解题思路有很大的帮助.

2.3 联通模拟

解析本题涉及椭圆、双曲线的方程与性质、直线的斜率、直线与椭圆的位置关系、垂直等知识，考查逻辑推理能力和运算求解能力，难度大，综合性强.由双曲线的渐近线与离心率的关系知，解决本题的关键是如何求渐近线的斜率.

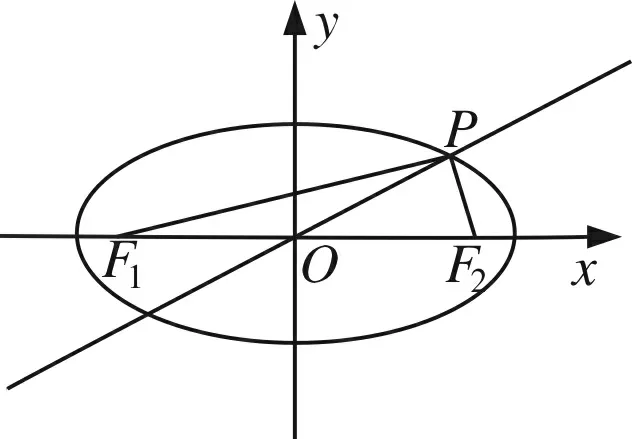
图1

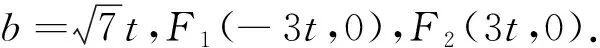
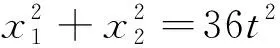
点评本题立足于椭圆，借助于垂直，分别从代数与几何的角度求出双曲线的离心率，而这两种方法的本质源于直线斜率的计算方法.本题通过双曲线的渐近线与离心率之间的关系，缩短了思维，减少了运算.

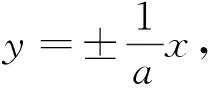
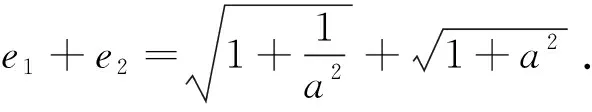
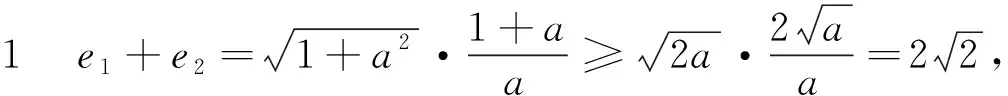
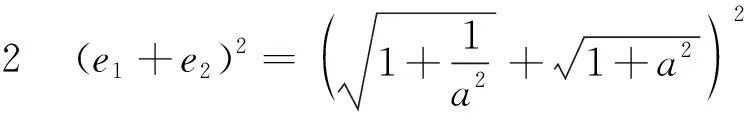
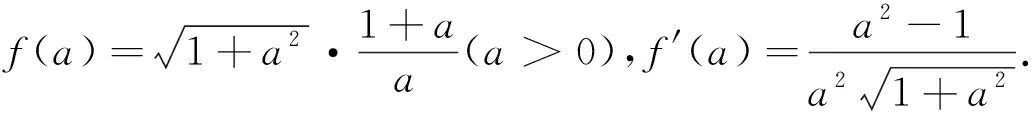
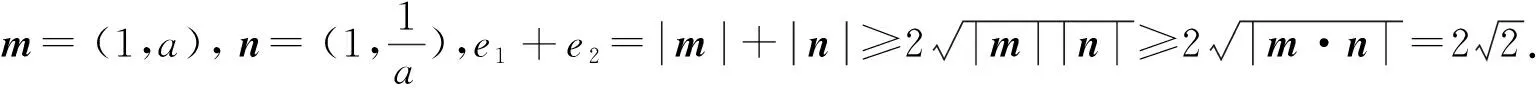
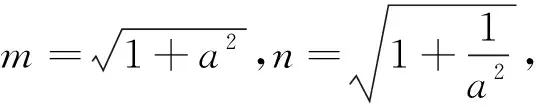
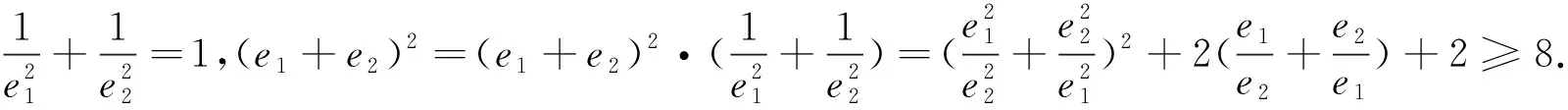
点评本题是双曲线的渐近线与离心率之间关系的直接应用，简化了思路，为求最值节省了时间与精力.又由求最值方法的多样性，培养了学生思维的灵活性，反映了命题的一般要求.

2.4 直击高考

解析本题考查双曲线的方程、顶点、渐近线以及离心率、圆的方程、直线与圆的位置关系、三角形等知识,对逻辑推理与运输求解能力有一定要求.

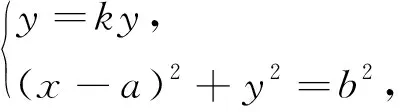
消去y得(1+k2)x2-2ax+(a2-b2)=0.

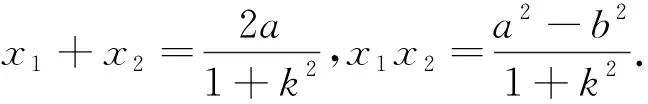
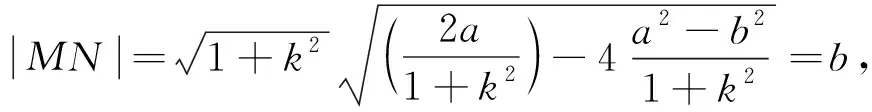
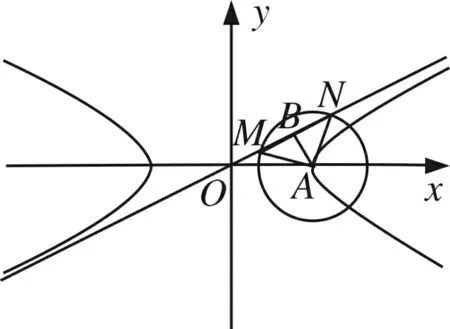
图2

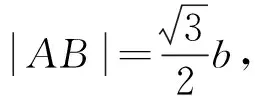
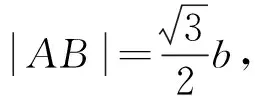
点评本题的突破口在于如何使用“∠MAN=60°”.通过圆的性质构造正三角形，建立双曲线的渐近线与离心率的联系，从而求出离心率.

解析本题考查的知识涉及双曲线方程、性质、圆以及直线与圆的位置关系、三角形等.

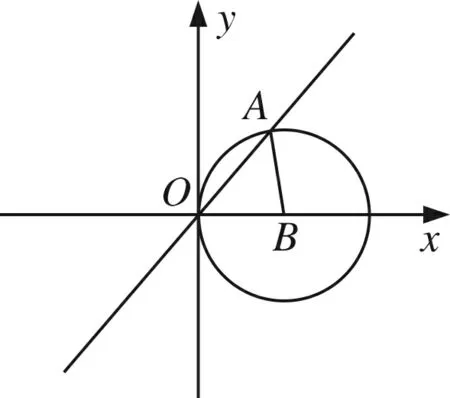
图3

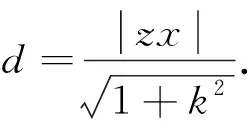
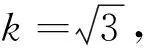
点评本题与上题相比，难度降低，若结合图形，会有助于解题.

3 反思

3.1 立足考情，有的放矢

高三复习，不仅要照顾到基础知识，也要注意知识之间的联系与综合.在具体操作中，要放弃经验至上的思想，要着眼于教材，立足考情，认真研读考试大纲与考试说明，做到心中有数，方能有的放矢.复习课不同于新课，复习课大都省略了知识生成过程，省略了概念等的归纳概括过程.复习课以学生已学为基础，如果再面面俱到、滴水不漏的展开，不仅费时费力，事倍功半，学生也容易生厌，影响学生的复习兴趣与积极性.故教师要立足考情，合理设计复习课堂，抓住内容的要点与关键点，以点带面，打造“生命课堂”.

3.2 立足联系，培养思维

《考试大纲》指出“注重学科的内在联系和知识的综合性，不刻意追求知识的覆盖面.从学科的整体高度和思维价值的高度考虑问题，在知识网络的交汇点处设计试题，使对数学基础知识的考查达到必要的深度.”[1]因此复习要立足于知识间联系，构筑知识网络.章建跃博士指出：“数学是培养思维能力的最佳载体.”而高三复习课基于知识的综合性与联系，思维量一般更大和对思维的灵活性要求也更高，因而对锤炼思维有很大的帮助，有利于培养学生的思维能力.

3.3 立足“小处”，以点带面

高三复习要巩固基础，提升能力.考虑到高三时间的紧迫性，内容的综合性，如若把复习课上成了新课，想必不利于备考，也不利于提升学生的能力.因此，教师要遵循复习课的规律，不拘泥于“细腻”，与其面面俱到，不如尝试从小处入手，以点带面，推动复习课有效开展.就像双曲线的渐近线与离心率，二者通过参数a、b、c与双曲线的方程以及其它性质建立了联系.复习不妨从二者入手，顺藤摸瓜，连带出其它知识，既省时省力，又能抓住关键，可谓一举两得.