基于频域子结构法的动量轮弹性边界微振动研究

李雄飞， 程 伟

(北京航空航天大学 航空科学与工程学院，北京 100083)

随着航天技术的不断发展，研制高精度高稳定性航天器成为当前一个重要的课题，也是航天技术发展的必然趋势，因此，在卫星的研制过程中对平台稳定性提出了越来越严格的标准[1-2]。然而，卫星在轨运行时产生的微振动会严重影响平台稳定性，从而降低卫星的指向精度和成像精度等关键性能指标[3]。卫星微振动具有幅值低和频带宽的特点，通常由其内部安装的活动部件运行时产生，比如动量轮，控制力矩陀螺，太阳翼驱动机构，制冷机等，其中，动量轮和控制力矩陀螺通常被认为是最主要的扰振源[4-5]。

动量轮常用于卫星的姿态控制，其工作原理为通过改变高速旋转飞轮的加速度产生反作用力矩。动量轮在提供控制力矩的同时，也会带来不利的振动，这些振动被称为动量轮微振动[6]。动量轮微振动主要由以下四个方面原因引起：①飞轮质量不平衡；②内部结构共振；③轴承缺陷；④电机扰动[7]。其中，飞轮质量不平衡被认为是最主要的因素，因此，动量轮微振动具有倍频谐波特性，由于飞轮支撑轴承的调制作用，动量轮微振动又具有子谐波特性[8]。动量轮在工作过程中是变速的，因此，动量轮微振动基频是变化的，且频率分布在中高频，使得对于动量轮微振动的控制和抑制十分困难。并且，动量轮微振动极易与其安装的卫星弹性界面发生结构耦合。动量轮微振动会激发出弹性安装界面的结构模态，产生较大的振动，安装界面的振动又会反过来作用于动量轮，产生更多的振动[9]。动量轮微振动与弹性界面的耦合机理较为复杂，且将进一步影响卫星的关键性能指标。因此，随着高分遥感卫星的不断发展，研究动量轮在弹性边界的耦合微振动特性意义重大。

国外对于动量轮在弹性边界的微振动进行了长期的研究，且取得了较多的成果。文献[10]采用加速度反馈法，建立了动量轮与弹性安装界面的单自由度弹簧质量模型，并对模型进行了仿真分析，分析结果表明：当动量轮模型中不考虑内部弹性，进行弹性边界耦合分析时，可将动量轮等效成刚体；当考虑内部弹性时，这种耦合分析方法会引起较大的误差。为了减小忽略动量轮内部弹性引起的误差，文献[11-13]提出了一种基于动质量测试技术的耦合分析方法，该方法引入修正项对动量轮刚性界面的测试频谱进行修正，将修正后的频谱输入到航天器传递函数模型预测其响应。其中，引入的修正项可通过动量轮界面和弹性界面的动质量测试得到。该方法在大部分频带内起到了较好的修正效果，然而，在某些频带内效果依然不好，其主要原因是动量轮界面动质量测试未能考虑飞轮陀螺效应的影响。文献[14-17]利用试验和仿真相结合的方法研究飞轮陀螺效应对耦合分析的影响，开发了一套地震微振动测量系统，应用该系统测试了动量轮在弹性安装界面的扰振，并建立了动量轮与该测试系统的理论模型，分析认为陀螺效应对耦合扰动分析具有较大的影响。国内对于动量轮在弹性界面微振动的研究相对较少。文献[18]应用动质量测试技术研究了微振动测试平台刚度对动量轮微振动测试的影响，研究表明，动质量测试与理论建模相结合的方法能较好地体现测试台刚度对测试结果的影响，对考虑耦合效应的微振动测试具有一定的借鉴意义。文献[19]提出了一种微振动源解耦加载的方法，实现了微振动源与航天器结构的解耦，该方法适用于动量轮、控制力矩陀螺等常见的微振动源加载。

本文将应用频域子结构方法研究动量轮在弹性边界的微振动特性，频域子结构方法的基本思想为综合子结构的频响函数得到整体结构的频响函数矩阵，整体结构的频响函数矩阵可用于计算其响应。在研究过程中将动量轮与弹性边界耦合振动系统划分成动量轮和弹性边界两个子结构，并分别计算两个子结构的频响函数。动量轮的频响函数通过建立其运动方程得到，弹性边界的频响函数通过有限元仿真得到。然后应用频域子结构法综合动量轮和弹性边界的频响函数得到耦合系统的频响函数矩阵，通过该频响函数矩阵进一步计算可得到耦合系统的微振动响应，最后运用数值仿真和多体动力学仿真进行了验证。本研究所得的结论为研究动量轮在弹性边界的微振动响应提供了一种新思路，对于研究航天器活动部件与弹性结构的耦合微振动特性具有一定的借鉴意义。

1 频域子结构法

早期的频域子结构方法是阻抗综合方法(IC方法)，该方法利用各个子结构的阻抗进行综合，存在对整个子结构频响函数矩阵求逆运算的问题，导致计算效率和精度不高[20]。文献[21]发展了一种在工程上广泛运用的导纳综合方法(RC方法)，该方法直接综合各个子结构的频响函数得到整体结构的频响函数矩阵，只需对界面自由度的频响函数求逆，求逆次数和维数大大减小，计算精度和效率得到较大提高。本研究应用RC方法计算动量轮-弹性边界耦合系统的频响函数矩阵，下面对RC方法进行简单推导，并引入界面坐标转换矩阵来表达不同坐标系下子结构的综合。

定义装配结构S及其划分的子结构I和子结构II，下标c代表界面坐标，i与j分别代表子结构I和子结构II的内部坐标。图1表示由子结构I和子结构II综合得到整体结构S的过程，坐标系o1x1y1z1(坐标系1)和o2x2y2z2(坐标系2)分别表示它们的局部坐标系。

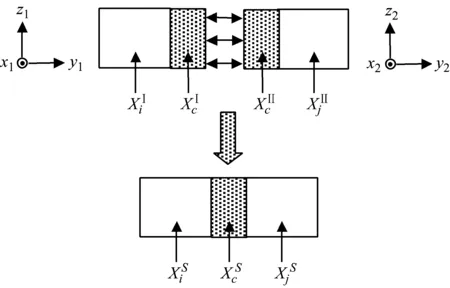
图1 两个子结构的综合过程

定义装配结构S，子结构I和子结构II的频响函数矩阵分别如下：

(1)

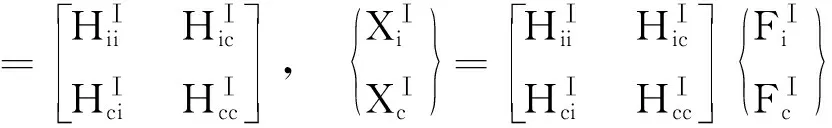
(2)

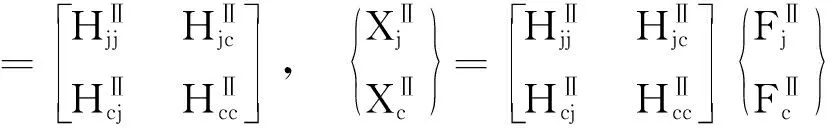
(3)

式中：H代表频响函数矩阵；X和F分别代表激励和响应向量。

RC方法的基本条件是界面位移协调性和力平衡性，当坐标系1和坐标系2不一致时，需要先将界面坐标转换成一致后才能综合。假设转换后的界面坐标均与坐标系1一致，则需要引入对子结构II界面坐标的转换矩阵，定义为C。C为子结构II和子结构I界面坐标之间的方向余弦矩阵，此时，连接处的位移协调和力平衡条件为：

(4)

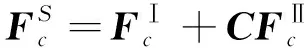
(5)

综合后，内部结点力和位移保持不变：

(6)

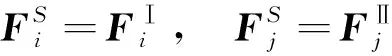
(7)

联立式(1)～式(7)可得到装配结构频响函数矩阵的表达式：

(8)

因此，将子结构的频响函数代入式(8)便可得到整体结构的频响函数矩阵。从式(8)可知，RC方法只需对界面自由度的频响函数求逆，提高了计算精度和效率，然而RC方法只适用于两个独立子结构之间的综合。下面总结RC方法的一般步骤：

1)根据需要将整体结构划分成两个独立的子结构；

2)计算子结构的频响函数矩阵和界面坐标转换矩阵；

3)将子结构的频响函数和界面坐标转换矩阵代入式(8)得到整体结构的频响函数矩阵。

2 动量轮扰振模型

2.1 建模方法及模型简化

本节应用拉格朗日方程建立动量轮的振动方程，广义形式的拉格朗日方程为[22]：

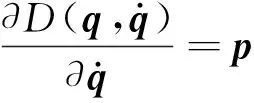
(9)

式中：向量q和p分别代表广义坐标和广义外力向量，表达式T，V和D分别表示系统的动能，势能和耗散能。

动量轮结构主要由飞轮、轴承以及框架组成。飞轮和框架之间由一对角接触球轴承支撑，运行时，飞轮绕转轴相对于框架高速转动。通常，飞轮转动频率远低于飞轮和框架的固有频率，因此飞轮和框架均可简化成6自由度刚体。参考文献[10]，中间的一对支撑轴承均可等效成具有轴向和径向刚度阻尼的线性弹簧，飞轮和框架之间可以等效成6自由度线性弹簧连接，其等效刚度和阻尼矩阵如下：

(10)

式中：kr和kz分别表示轴承的径向和轴向等效刚度；cr和cz表示它们的等效阻尼；d表示飞轮质心到轴承的距离。

基于以上简化和等效，自由状态动量轮模型可以简化成12自由度的质量-弹簧-阻尼系统，如图2所示，o0x0y0z0(坐标系0)为基座坐标系，原点o0位于飞轮和框架质心(假设飞轮和框架质心重合)。

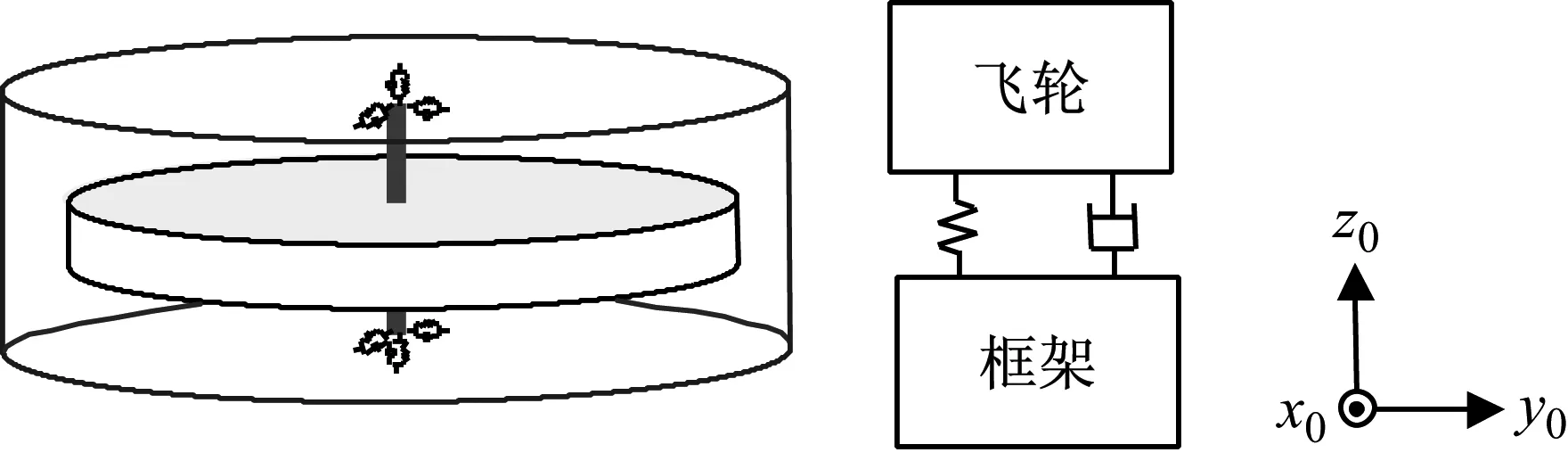
图2 动量轮简化模型

2.2 系统动能

动量轮振动系统的动能由下式决定：

(11)

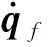
飞轮和框架的质量矩阵分别定义为：

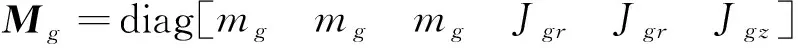
(12)

式中：mf和mg分别为飞轮和框架的质量；Jfr和Jgr分别为它们的径向惯量；Jfz和Jgz分别为它们的极向惯量。

飞轮和框架质心在坐标系o0x0y0z0中的六自由度位移向量分别定义如下：

(13)

式中：qft和qgt分别表示飞轮和框架质心处的平移位移向量，qfr和qgr表示它们的角位移向量。

对式(13)中的位移向量进行求导，可得到飞轮和框架质心在坐标系o0x0y0z0中的六自由度速度向量，分别表达如下：

(14)

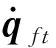
应用欧拉角表示飞轮和框架的定点转动角速度，如图3所示，三次转动的旋转角分别为β，α和γ，对应的旋转轴分别y0轴，xβ轴和zα轴，旋转后的坐标系分别为坐标系oβxβyβzβ，oαxαyαzα和oγxγyγzγ。

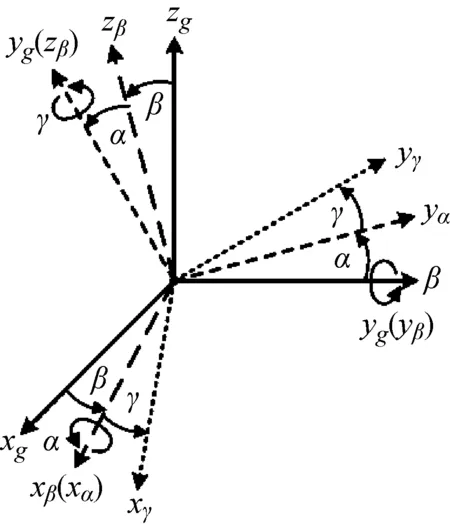
图3 欧拉角表示的飞轮和框架定点转动

由欧拉角表示三次旋转后，飞轮和框架质心处角速度向量分别在坐标系oαxαyαzα中表示如下：

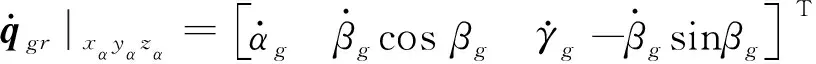
(15)

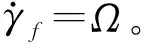
将式(12)，式(14)和式(15)代入到式(11)并整理后可得到整个系统的动能：

(16)

2.3 系统势能和耗散能

动量轮振动系统的势能和耗散能分别表示如下：

(17)

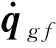
qgfx0y0z0=qg-qf

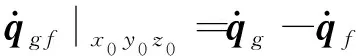
(18)

整个系统的势能和耗散能可通过式(10)，式(17)和式(18)得到，分别表示如下：

V=kr[(xf-xg)2+(yf-yg)2]+kz(zf-zg)2+

d2kr[(αf-αg)2+(βf-βg)2]

(19)

(20)

2.4 系统广义外力

定义系统的广义外力向量如下：

(21)

式中：fft和fgt分别表示作用在飞轮和框架质心处的外力向量，ffr和fgr表示力矩向量。

系统广义外力主要来源于飞轮的不平衡特性，主要包括静不平衡特性和动不平衡特性。由于转子在加工、制造和装配过程中的误差，转子的质心偏离旋转轴，转子高速旋转时，偏置质量会产生离心惯性力，从而对转子产生干扰，这种现象称之为静不平衡，如图4(a)所示。另一方面，由于转子存在一定的轴向厚度，偏置质量可能会处于垂直于转轴的不同平面内，偏置质量产生的惯性力由于不在同一个旋转平面内，从而会产生径向的惯性力矩，这种情况称之为动不平衡，如图4(b)所示。

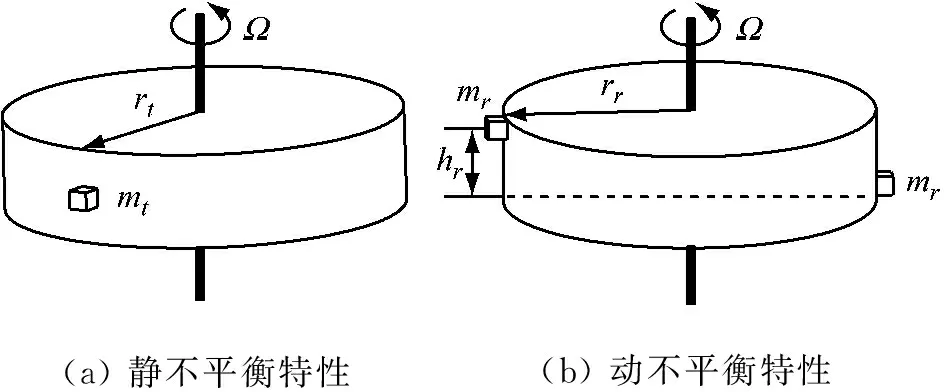
(a) 静不平衡特性(b) 动不平衡特性

图4 飞轮静不平衡和动不平衡特性

Fig.4 The static and dynamic imbalance of the flywheel

图4(a)中，mt为垂直于旋转轴同一平面内的等效偏置质量，rt为mt偏离旋转轴的距离。图4(b)中，mr为沿轴向不同平面内的等效偏置质量，rr为mr偏离旋转轴的距离。hr为两个动不平衡偏置质量的轴向距离。若转子自转角速度的大小为Ω，则由静不平衡所产生的不平衡力和动不平衡所产生的动不平衡力矩的大小分别为：

fft=[UtΩ2sin(Ωt+φt)UtΩ2cos(Ωt+φt) 0]T，

ffr=[UrΩ2sin(Ωt+φr)UrΩ2cos(Ωt+φr) 0]T

(22)

式中：Ut=mtrt和Ut=mrrrhr分别为静不平衡质量和动不平衡质量，φt和φr分别为它们的初始相位。

由于框架上没有外部激励，因此fgt和fgr均为零向量。

2.5 动量轮的振动方程

将式(16)，式(19)，式(20)和式(21)代入到式(9)中，可得到动量轮的振动方程，忽略高阶小量并整理后可以表示成如下矩阵形式：

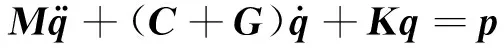
(23)

式中，M，C和K分别代表动量轮振动系统的质量，阻尼和刚度矩阵，G表示陀螺矩阵，它们的表达式分别如下：

(24)

其中，Gf为飞轮的陀螺矩阵，其具体表达式如下：

(25)

该振动系统的广义坐标向量q如下：

(26)

3 动量轮与弹性边界耦合系统的振动特性

3.1 划分子结构

图5为动量轮与弹性边界耦合系统的示意图，弹性边界由铝蜂窝夹芯板和支架组成，动量轮通过支架倾斜安装于弹性边界。为了研究耦合系统的微振动特性，可将其划分成动量轮子结构(子结构I)以及弹性界面子结构(子结构II)，其局部坐标分别为坐标系o0x0y0z0(坐标系0)和坐标系o3x3y3z3(坐标系3)。

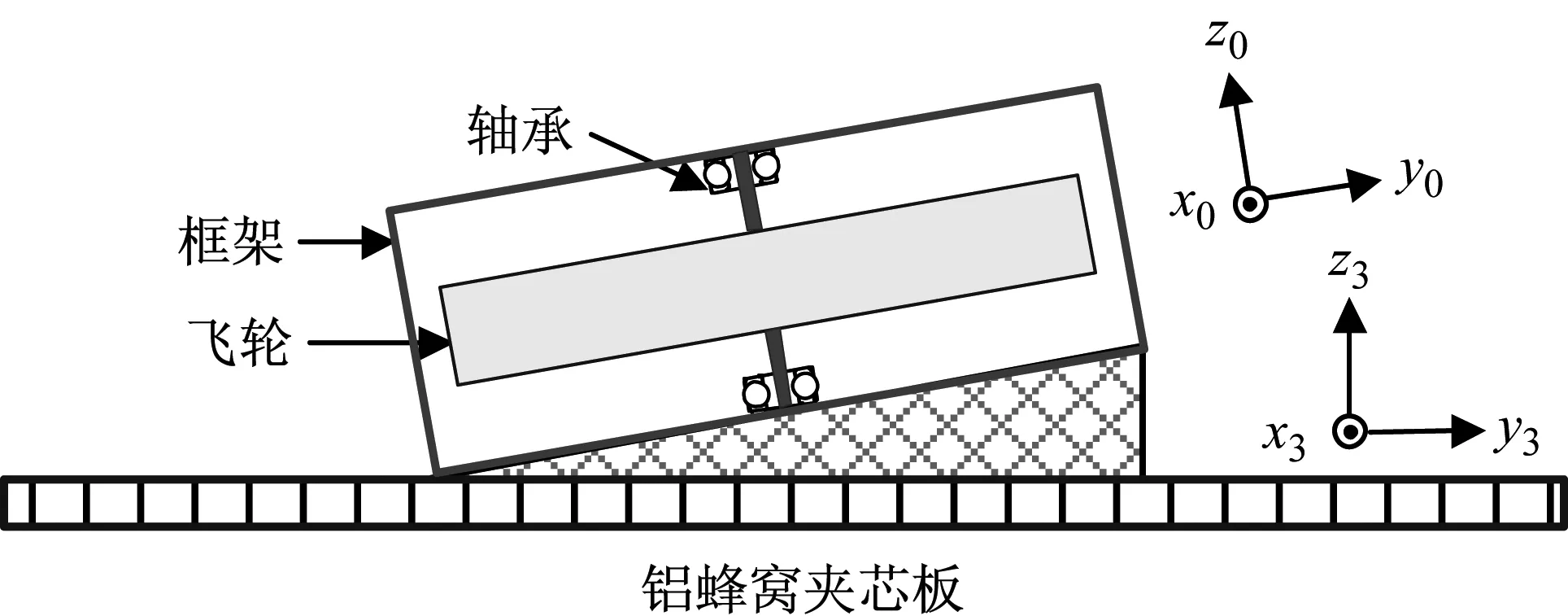
图5 耦合系统简化模型

3.2 子结构I

子结构I的频响函数可以通过其运动方程求得。子结构I的内部节点为飞轮质心，界面节点为框架底面中心，然而运动方程中广义坐标为飞轮和框架的质心，因此，引入新的广义坐标向量：

(27)

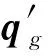
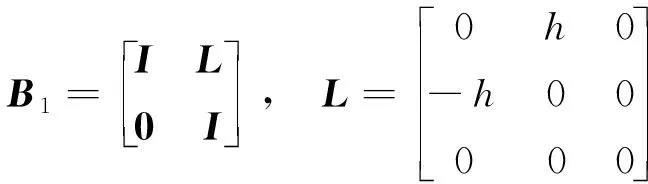
(28)

式中：h表示飞轮和框架的质心到动量轮安装点的距离，此时，广义坐标向量q1和q之间的关系如下：

(29)

对应于新的广义坐标向量，引入新的广义外力向量：

(30)

类似的，广义外力向量p1和p之间存在如下关系：

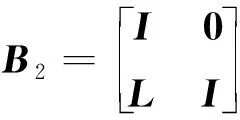
(31)

将式(29)和式(31)代入到式(23)，可以得到新的广义坐标下的运动方程：

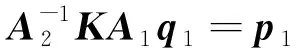
(32)

对式(32)所示子结构I的时域运动方程进行傅里叶变换，可得到其频域形式的运动方程，整理成如下形式：

ZⅠQ1(s)=P1(s)

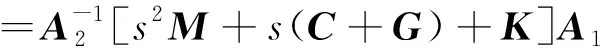
(33)

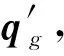
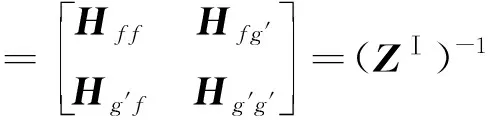
(34)

3.3 子结构II

本文研究动量轮安装点的振动特性，因此子结构II只考虑与动量轮连接处的界面坐标，其频响函数将通过子结构II的有限元模型计算得到。

子结构II由铝蜂窝夹芯板和支架组成，支架在有限元模型中等效成质点，其质量和三个方向惯量分别给定为1 kg，0.001 kg·m2，0.001 kg·m2和0.002 kg·m2；铝蜂窝夹芯板尺寸为0.8 m×0.4 m×0.03 m，其结构主要由两层铝蒙皮以及其中间的蜂窝芯子夹层组成，铝蒙皮厚度为0.3 mm。蜂窝芯子可以等效成均匀正交各向异性材料，因此整块铝蜂窝夹芯板可等效成由三层板组成的层合板[23-24]。给定符号E，G，ρ和υ分别代表弹性模量，剪切模量，密度和泊松比，铝蒙皮和蜂窝芯子材料参数，如表1所示。

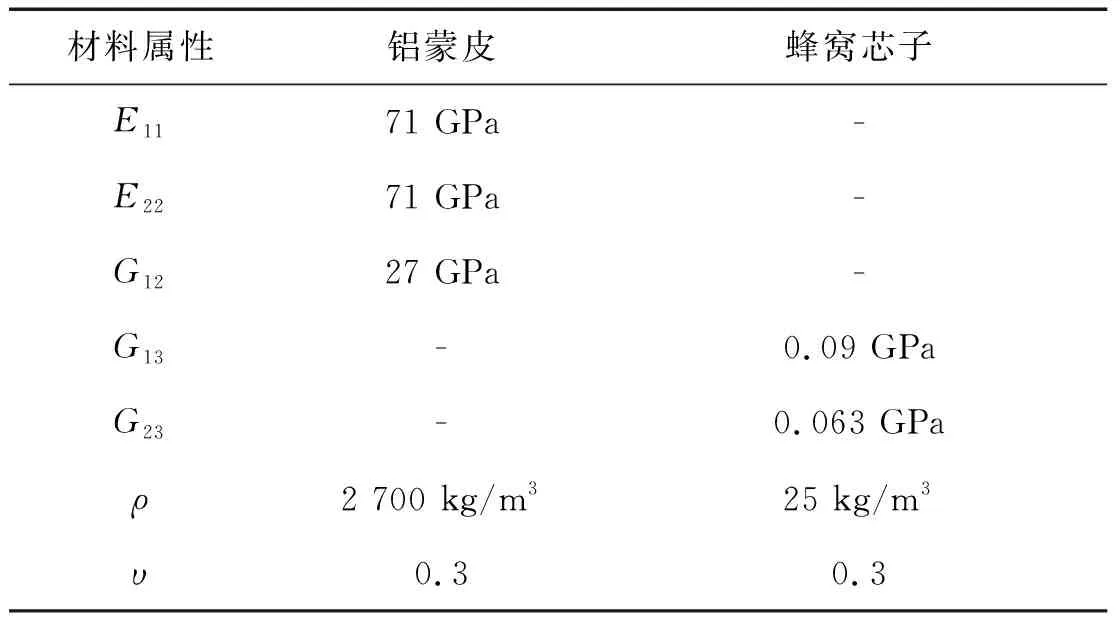
表1 铝蒙皮和蜂窝芯子的材料参数

应用商用软件PATRAN建立铝蜂窝夹芯板的有限元模型。该有限元模型四条边上的所有节点均施加六自由度位移约束，节点间距为0.1 m。动量轮支架安装在该板中心，对有限元模型进行谐响应分析，分别对中心点施加六个自由度方向的单位力/力矩求其六自由度响应，可得到该点的六自由度频响函数矩阵，表示如下：

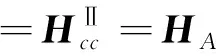
(35)

3.4 耦合系统的频响函数矩阵和响应

由于动量轮倾斜安装于弹性边界，因此子结构I和子结构II局部坐标系之间沿x轴存在夹角θ，其局部坐标系之间的角度关系如图6所示。从图6可得到子结构II和子结构I界面坐标之间的方向余弦矩阵，即耦合系统的界面坐标转换矩阵，表达式为：

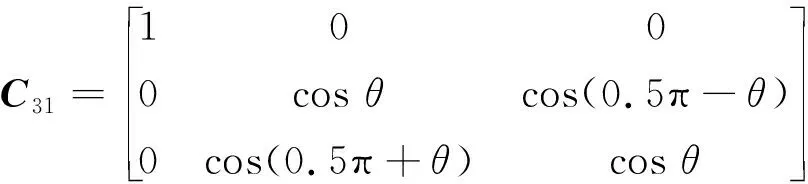
(36)

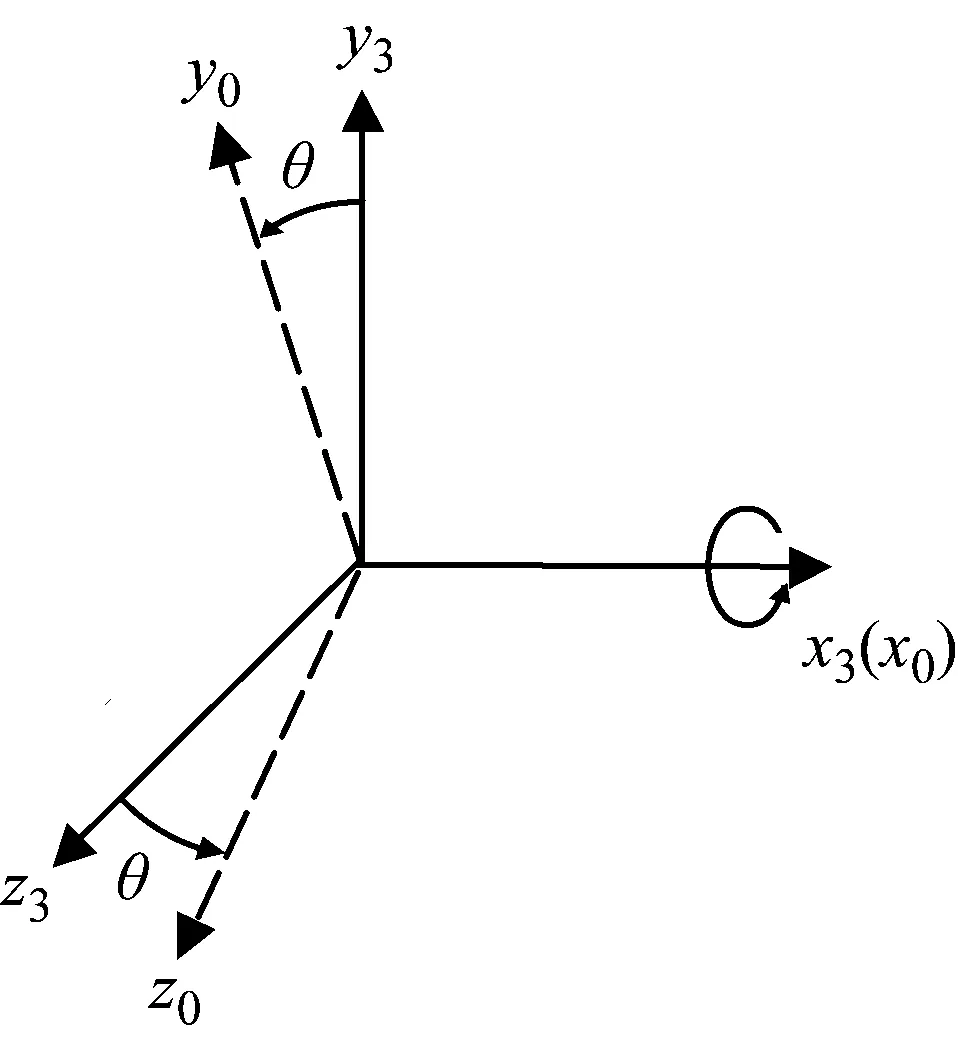
图6 局部坐标系3和0之间的角度关系

将式(34)，式(35)和式(36)代入到式(8)，可得到耦合系统的频响函数矩阵，表达式为

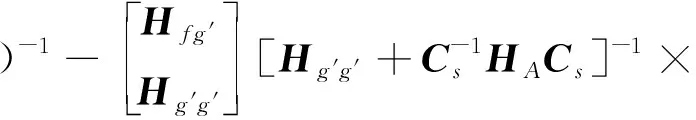
[Hg′fHg′g′]

(37)

该耦合系统中，只有飞轮上存在激励，因此耦合系统的激励在时域上可以表示为：

(38)

假设φt和φr均为0，耦合系统的激励可以表示成频域形式：

(39)

耦合系统的位移响应向量可以通过式(37)和式(39)相乘得到：

Xs(s)=HsPs(s)

(40)

将位移响应向量右边乘以s2，可得到耦合系统的加速度响应向量：

(41)

4 仿真验证

为了验证RC方法建立的耦合系统的频响函数矩阵，应用商用软件Matlab对式中所表示的动量轮安装点的加速度响应进行数值仿真，并应用多体动力学仿真进行验证。对动量轮转速稳定在Ω=k·10π rad/s(k=1，2，…，10)时进行仿真，仿真参数，如表2所示。

表2 耦合系统仿真参数

利用商用软件Adams对耦合系统进行多体动力学仿真验证，在Adams模型中，用刚体部件模拟飞轮和框架，具有柔度特征的轴承单元模拟轴承。弹性边界由PATRAN模态分析得到的弹性界面子结构的模态中性文件导入得到，不平衡特性由在飞轮上附加质量得到。采样频率和采样时间分别为2 048 Hz和16 s。后处理时，对时域形式的仿真结果进行傅里叶变换将其转换成频域形式。

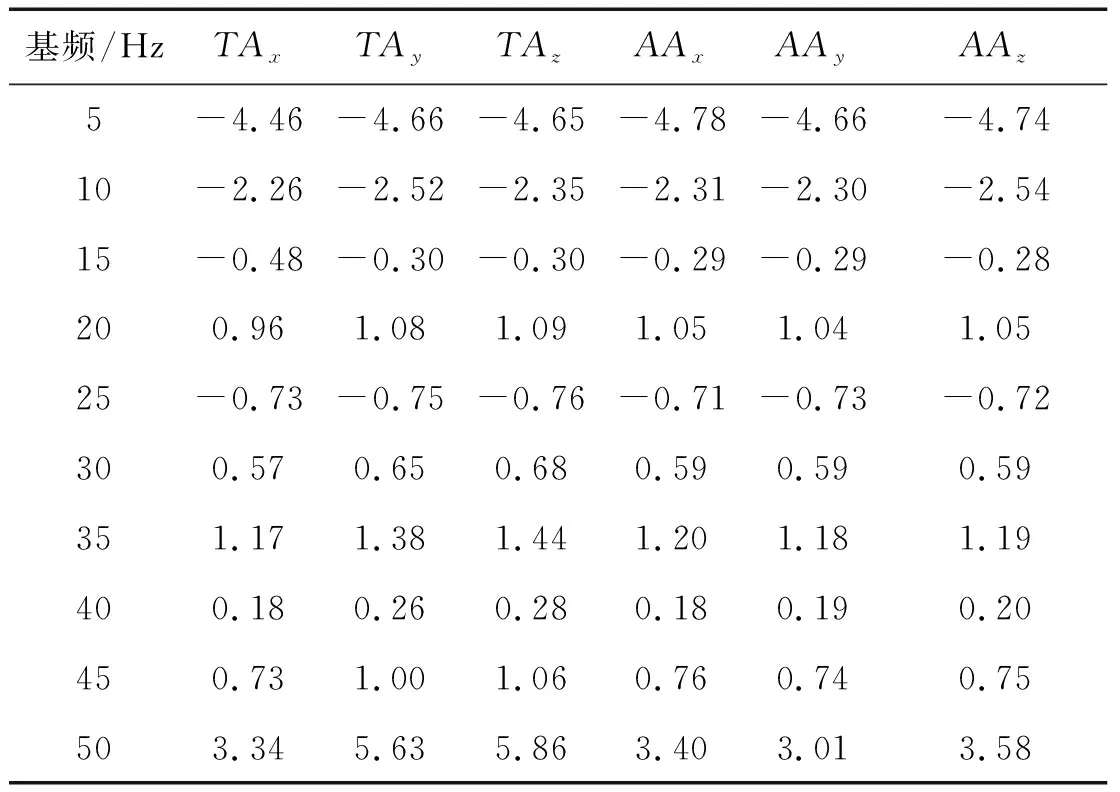
图7为Matlab和Adams仿真得到的动量轮在各个转速下平移加速度基频幅值切片对比图，图8为角加速度幅值切片对比图。从图中结果可知，动量轮加速度基频幅值随转速变大，Adams仿真和Matlab仿真结果基本一致。对仿真结果进行误差分析，如表3所示，RC方法计算得到的耦合系统响应的仿真误差在±6%以内，因此，RC方法可用来预测动量轮在弹性边界的耦合响应，且具有较高的精度。

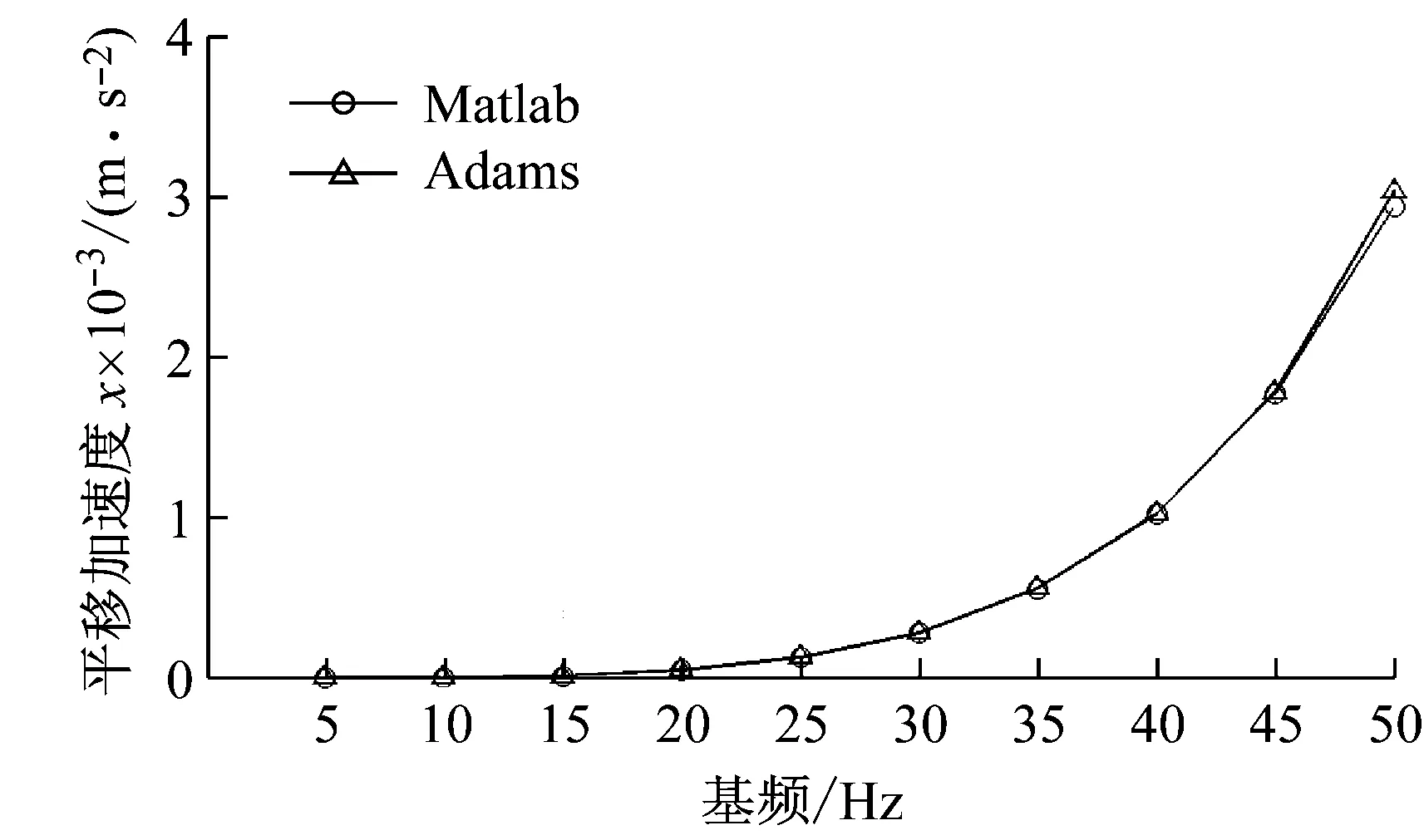
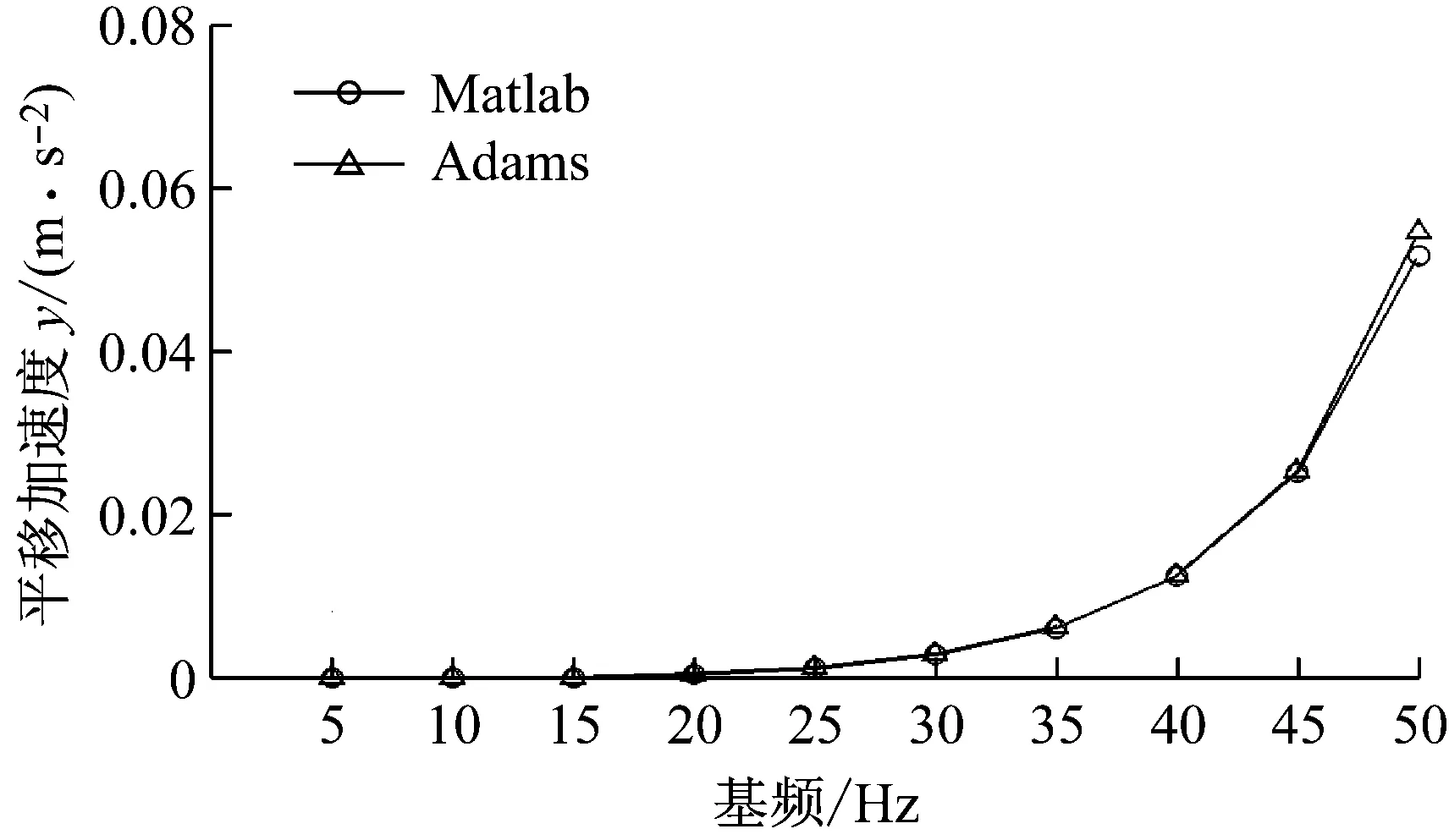
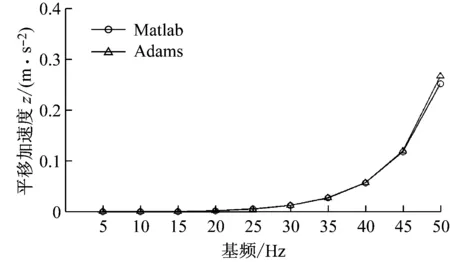
图7 Matlab和Adams平移加速度幅值仿真结果对比

5 结 论

本研究应用频域子结构法研究动量轮在弹性边界的微振动特性，采用RC方法推导了动量轮和弹性边界耦合系统的频响函数矩阵，通过该频响函数矩阵得到了耦合系统的加速度响应，并应用数值仿真和多体动力学仿真对加速度响应进行了验证，两种仿真的结果基本一致，且耦合系统响应的仿真误差在±6%以内。结果表明：频域子结构法适用于分析动量轮在弹性边界的微振动响应，并且具有较高的分析精度和计算效率。本研究所得的结论为研究动量轮在弹性边界的微振动响应提供了一种新思路，对于研究航天器活动部件与弹性结构的耦合微振动特性具有一定的借鉴意义。

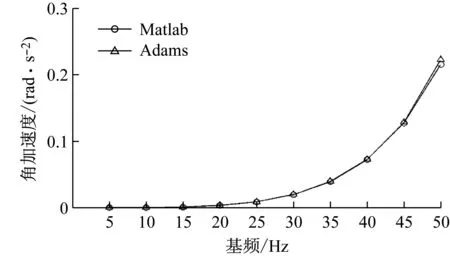
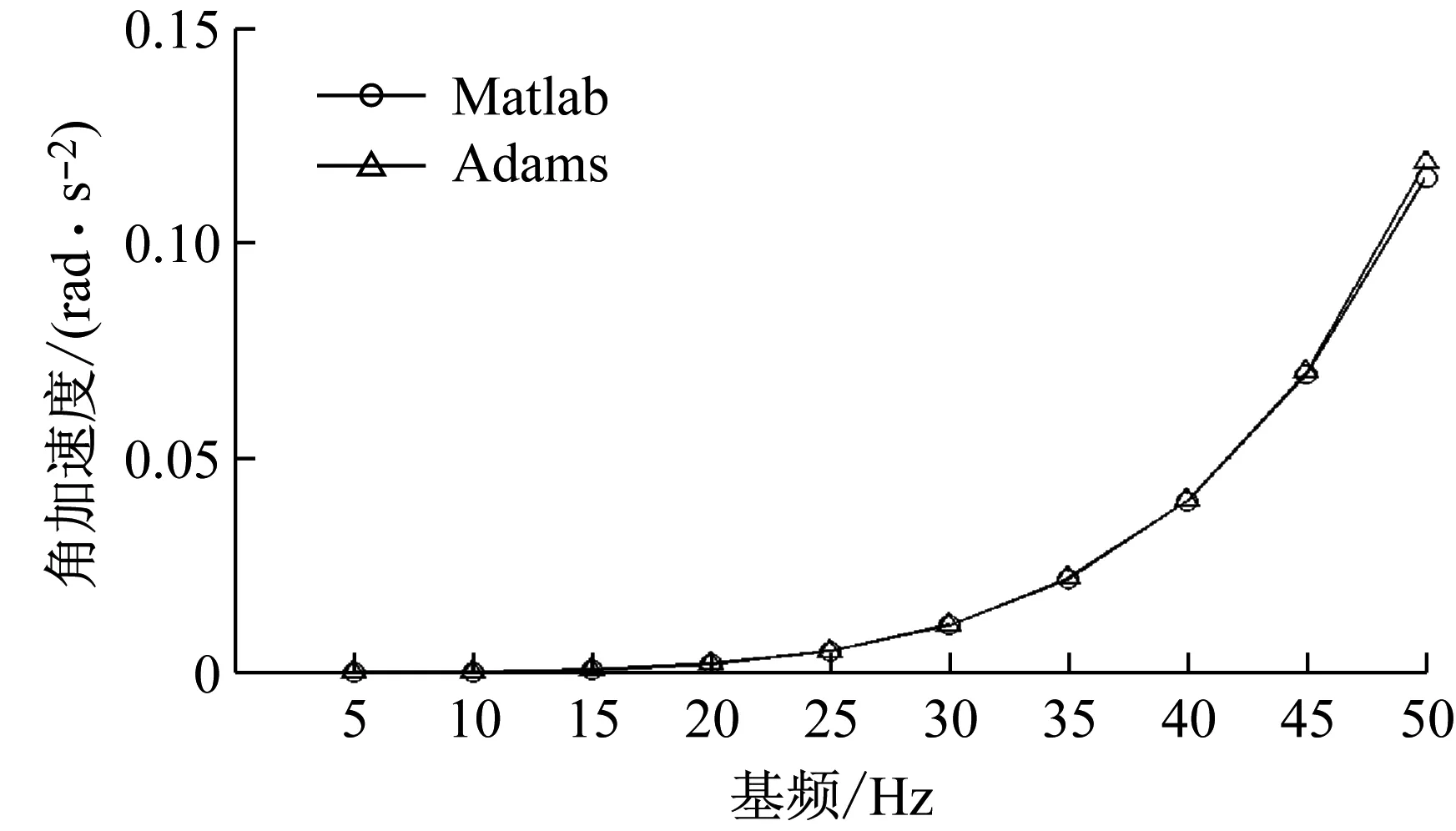
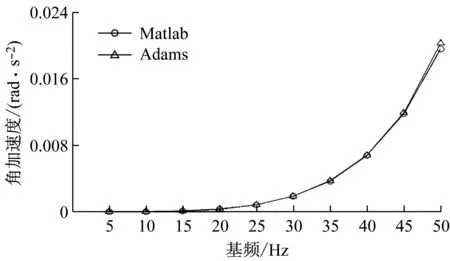
图8 Matlab和Adams角加速度幅值仿真结果对比

基频/HzTAxTAyTAzAAxAAyAAz5-4.46-4.66-4.65-4.78-4.66-4.7410-2.26-2.52-2.35-2.31-2.30-2.5415-0.48-0.30-0.30-0.29-0.29-0.28200.961.081.091.051.041.0525-0.73-0.75-0.76-0.71-0.73-0.72300.570.650.680.590.590.59351.171.381.441.201.181.19400.180.260.280.180.190.20450.731.001.060.760.740.75503.345.635.863.403.013.58