钢阻尼器考虑水平2方向变形的简化滞回模型研究

陈书娴, 周 鑫, 谢 旭

(1. 浙江大学 建筑工程学院， 杭州 310058; 2. 桐庐县交通发展集团有限公司， 桐庐 311501)

钢阻尼器具有力学性能稳定、耐久性好、维护简单、耗能效果显著、成本低等优点，是目前建筑物以及桥梁减隔震设计中较常用的减隔震装置。在结构地震反应计算中，钢阻尼器一般采用单方向力学模型[1]，不考虑其发生水平2方向变形的力学行为。但是，在曲线桥、斜桥及其他不对称桥梁中应用钢阻尼器进行减隔震设计时，即使按单方向输入地震作用，钢阻尼器也会因结构水平转动而产生2个方向的变形。因此，单方向力学模型不能准确模拟阻尼装置的力学行为。然而,目前关于钢阻尼器同时考虑水平2方向变形的简化滞回模型的研究十分少见，在结构地震反应计算中只能采用三维有限元模型考虑其不同方向变形之间的相互影响，计算效率低。

为了简化框架结构在地震作用下水平2方向的弹塑性反应计算，Wada等[2]提出了多重剪切弹簧(Multi-Shear-Spring，MSS)力学模型。该模型用多个弹塑性单向弹簧模拟结构在水平2方向变形时的力学性能。此后，一些学者基于该模型提出了适用于不同耗能构件和结构的计算方法。如Ito等[3]利用预测误差法系统识别技术提出了基于三折线滞回模型的MSS模型，以此较精确地模拟了建筑物基础隔震系统的滞回特性；藤田隆史等[4]、Yamamoto等[5-7]根据试验结果与MSS模型滞回曲线履历耗能相等的原则分别提出了适用于高阻尼橡胶支座、铅芯橡胶支座的弹簧参数计算方法；Ene等[8-9]用MSS模型模拟了由4个U型钢阻尼元件对称布置的减隔震装置整体力学特性。但是上述研究成果均仅适用于水平面内各方向变形性能相同的对象，缺乏通用性。

鉴于上述MSS模型的不足，Haso等[10]以城市建筑群的地震反应计算为目的，提出了一种扩展MSS模型。该模型通过一组刚度不等的弹簧模拟了楼层水平正交2方向的结构刚度，但其对弹簧屈服点的确定方法以及滞回本构模型没有进行深入分析，无法模拟钢阻尼器的力学特性。

钢阻尼器作为一种常用的减隔震装置，各方向的滞回特性一般存在显著差异，且其滞回模型具有钢材弹塑性性变形的基本特性。为此，本文结合钢材的弹塑性变形性能提出了一种改进的MSS(Modified Multi-Shear-Spring，MMSS)模型，用于模拟钢阻尼器在地震作用下的力学行为，为其地震反应分析提供了简便的计算方法。

1 MMSS模型

1.1 MSS力学模型

Wada等提出的MSS力学模型的构成如图1所示。该模型由n个非线性特性相同的水平弹簧径向均匀排列而成，选用双折线模型作为弹簧的滞回曲线，其荷载-位移关系为

(1)

式中：ΔfX、ΔfY为MSS模型沿X轴、Y轴的恢复力增量，ΔδX、ΔδY为其沿X轴、Y轴的位移增量，kj和φj分别为第j个弹簧的刚度和其所处位置与X轴所成的夹角。

当MSS模型发生单向变形时，虽然各弹簧的非线性参数值相同，但由于每个弹簧所处的位置的不同，使得它们达到屈服点的时刻产生差异[11]。因此，当弹簧数量n较少时，模型计算所得的滞回曲线为多折线，与真实滞回曲线之间存在偏差。这时，需要适当增加弹簧数量，以使滞回曲线变得光滑。

(a) 立体图(b) 平面图

图1 MSS力学模型示意图

Fig.1 Diagram of Multi-Shear-Spring mechanical model

1.2 MMSS模型

本文提出的改进的MSS模型(即MMSS模型)的构成如图2所示。该模型由在X、Y、45°、-45°方向的4个非线性特性不同的水平弹簧径向排列而成。由于钢阻尼器一般为单轴对称形式，因此在每个方向上仅设置一个弹簧。为了使得滞回曲线能够反映出钢材在反复荷载下的弹塑性变形性能，MMSS模型引入Menegotto-Pinto(MP)滞回模型作为各弹簧的滞回曲线，通过其与钢阻尼器多方向弹塑性变形性能一致的原则确定模型的相关参数。

以下将分别讨论弹簧的滞回曲线以及曲线各参数的确定方法。

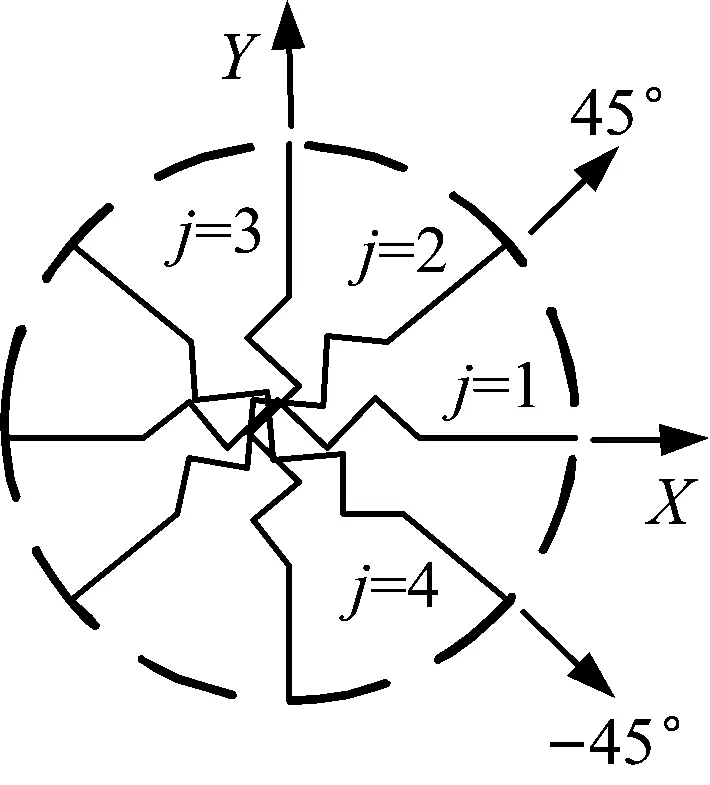
图2 MMSS模型示意图

1.2.1 滞回曲线

MP滞回模型是钢筋混凝土结构地震反应计算中常用的钢筋本构模型，能较好地反映钢材的弹塑性力学特性。该模型的荷载f和位移δ的履历关系如图3所示，其公式为[12]：

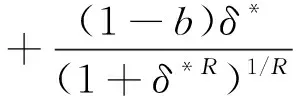
(2)

这里，

(3)

式中：(δr,fr)为荷载-位移曲线的反向加载点，(δs,fs)为弹性渐近线与屈服渐近线的交点；k1为弹簧的初始刚度；k2为弹簧的屈服后刚度；δm为加载历史中变形极大值或极小值(取决于该时刻位移增量的正负)；R0、cR1和cR2为确定曲线形状的参数；R为综合考虑R0、cR1和cR2的形状参数。

形状参数R对曲线形状的影响如图4所示[12]，其取值直接影响模型的模拟精度。

为了考虑等向强化效应，引入ΔN和ΔP对(δs,fs)

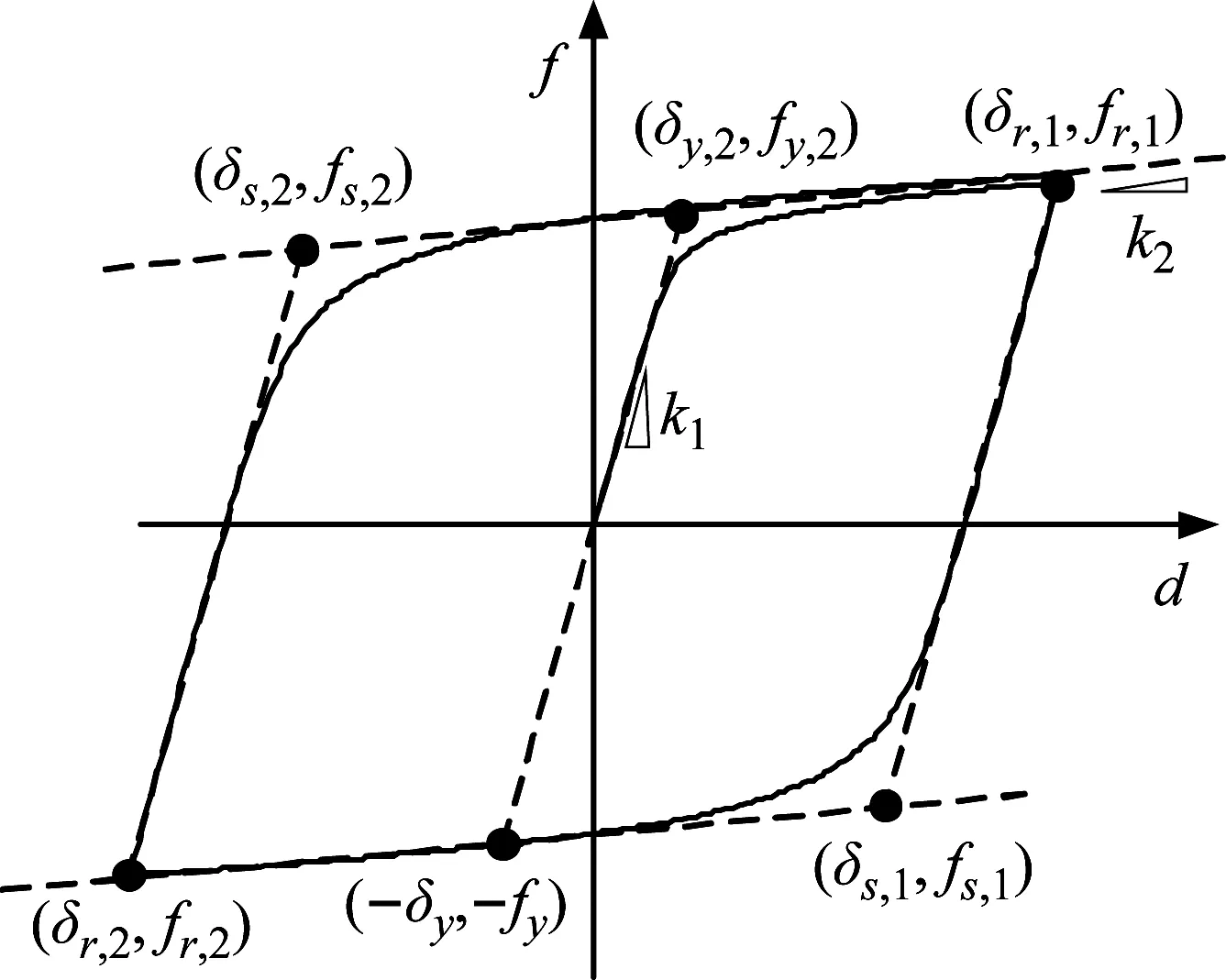
图3 MP模型的荷载-位移曲线

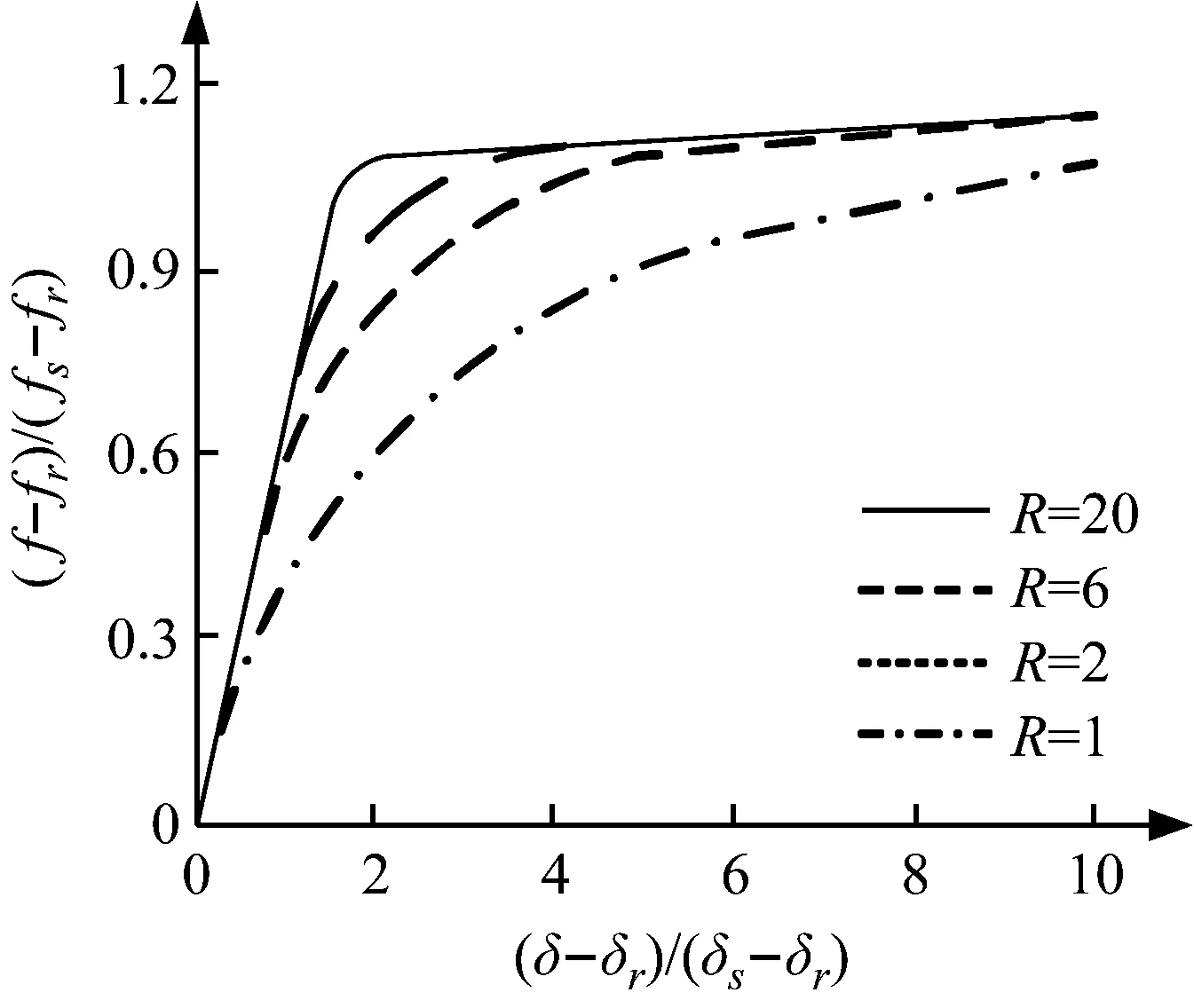
图4 参数R对曲线形状的影响

进行修正。修正规则如式(4)和式(5)所示：

(4)

(5)

将MP滞回模型作为单个弹簧的滞回曲线，需要确定其初始刚度k1、屈服点、屈服后刚度k2以及形状参数.下文将详细讨论上述参数的确定方法。

1.2.2 初始刚度及屈服点

本文中，将钢阻尼器的面内方向、面外方向、与面内成45°夹角的方向和与面内成-45°夹角的方向(顺时针为正)分别对应于MMSS模型的X、Y、45°、-45°方向(以下方向均用MMSS模型的方向标识)，则MMSS模型各弹簧的初始刚度(即图3中的k1)根据阻尼器与MMSS模型在4个方向的初始荷载-位移曲线一致确定，即：

(6)

式中:φj= (j-1) π/n，其中j=1～4；kj,1为第j个弹簧的初始刚度；KXX、KYY、KXY、KYX分别对应为阻尼器在X、Y、45°、-45°方向的初始刚度。

另外，根据力的等效关系，各弹簧的屈服力fj,y与阻尼器对应方向的屈服力fXX,y、fYY,y、fXY,y、fYX,y之间的关系如式(7)所示：

(7)

由式(7)确定了各弹簧的屈服力fj,y后，进一步可根据初始刚度和屈服力计算得到各弹簧的屈服位移δj,y。

1.2.3 屈服后参数

MMSS模型各弹簧的屈服后刚度(即图3的k2)仍可通过等刚度的原则确定，只需将式(6)中的kj,1改为kj,2、KXX～KYX改为钢阻尼器在对应方向的屈服后刚度即可。

另外，根据力的等效关系，阻尼器沿X、Y、45°、-45°方向单向加载到设计位移δd时的恢复力fXX,d、fYY,d、fXY,d、fYX,d与各方向弹簧屈服后刚度kj,2的关系如式(8)所示，由该式可计算出各弹簧达到设计位移的恢复力。

(8)

1.2.4 形状优化

为了提高MMSS模型的计算精度，在通过上述方法确定各弹簧的基本力学参数后，MP滞回模型还需要确定形状参数cR1、cR2以及R0的值。本文中，cR1、cR2根据文献[13]的建议分别取为0.925与0.15，而R0值通过优化计算得到。优化计算通过自适应遗传算法实现[14]。图5为优化计算的框图，优化目标函数为：

(9)

式中：i=1,2,3,4分别表示阻尼器在X、Y、45°、-45°变形时的滞回曲线，m表示一个滞回环的离散点数，F、F*分别表示由MMSS模型计算所得滞回曲线和钢阻尼器的实际滞回曲线。式(9)表示R0值由MMSS模型计算的滞回曲线与钢阻尼器实际滞回曲线的差异最小。

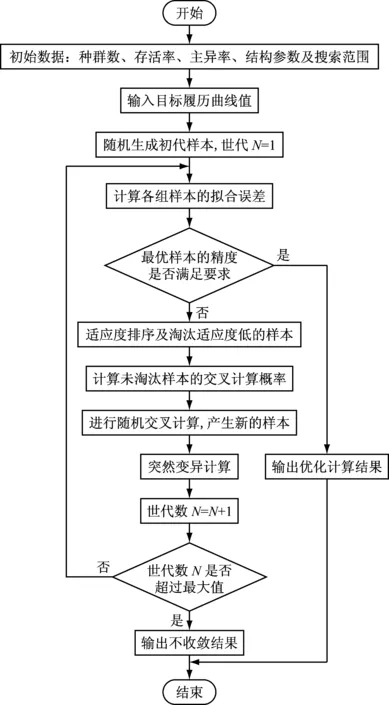
图5 基于自适应GA算法的R0优化计算程序框图

优化程序的准确性通过算例进行验证，结果如表1所示。表中，正算表示已知各弹簧的R0值求MMSS模型滞回曲线的过程，反算表示已知所拟合的目标曲线F*优化得到的各弹簧R0值。结果表明，该优化程序具有良好的逆计算能力，反算结果与精确值基本一致。

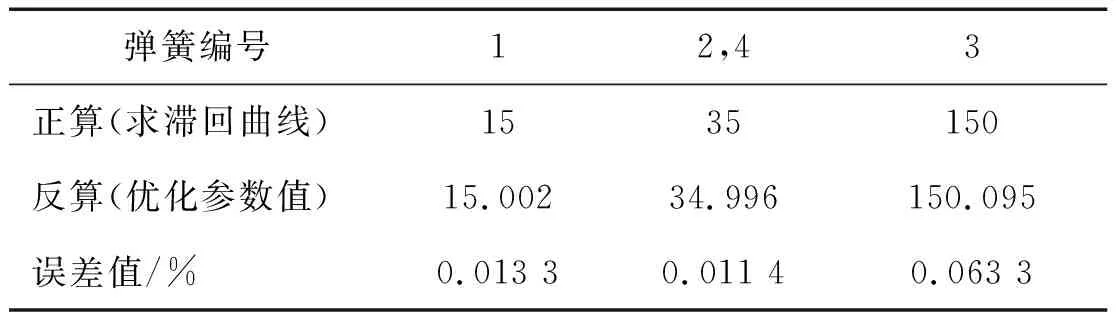
表1 程序有效性验证结果

2 有效性验证

下文将以建筑物中常用的U型钢阻尼元件为例，验证本文提出的MMSS模型的有效性。

2.1 钢阻尼器的力学性能分析

2.1.1 阻尼元件的组成及耗能特性

U型钢阻尼元件由上平直段、弯曲段和下平直段三部分组成，其构造如图6(a)所示[15]。图中，平直段末端的螺栓用于与其他构件相连。当元件发生面内方向(以下称x方向)位移时，其变形表现为平直段的拉弯和压弯；当元件发生面外方向(以下称y方向)位移时，其变形表现为弯曲段的扭转与螺栓连接位置处的剪切变形；当元件发生斜方向位移时，其变形表现为上述两个方向变形形式的耦合。阻尼元件在上述各方向的变形如图6所示，图中虚线处表示其产生塑性变形的主要位置[15]。

2.1.2 阻尼元件的力学特性

为了得到U型钢阻尼元件的力学特性，本文通过ABAQUS 6.13有限元软件对其不同方向的变形性能进行分析。有限元模型采用实体单元离散，单元类型为C3D8R，其网格划分以及几何尺寸如图7所示。图中，两处网格划分较稀段对应为施加强迫位移段和固定段，选用的几何参数为实际工程中应用较多的U型钢尺寸[8]。材料选用Q345qC，滞回本构模型采用Chaboche混合强化模型[16]，其参数如表2所示。表中，E为弹性模量，υ为泊松比，b0为双折线随动强化模型屈服后刚度与初始刚度的比值，σ|0为等效塑性应变为0时的应力，Q∝为屈服面的最大变化值，biso为屈服面随塑性应变发展变化的比率，Ckin为随动强化模型的初始值，γ为塑性变形增加时随动强化减小的比率。计算中同时考虑材料非线性和几何非线性的影响，设计位移为0.2 m。

由有限元分析结果可知，阻尼元件发生x方向变形时的最大应力出现在上、下平直段；其发生y方向变形时的最大应力出现在弯曲段以及平直段与固定段的交界位置；其沿45°和 -45° 2个方向(以下统称为斜方向)的变形性能基本一致。阻尼元件通过有限元分析得到不同方向的荷载-位移曲线如图8所示，图中，δx、δy、δ45(δ-45)分别表示在x方向、y方向以及斜方向施加的强制位移，fx、fy、f45(f-45)对应为各方向产生的恢复力。

(a) 面内变形

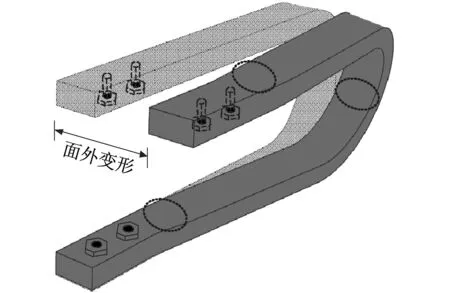
(b) 面外变形

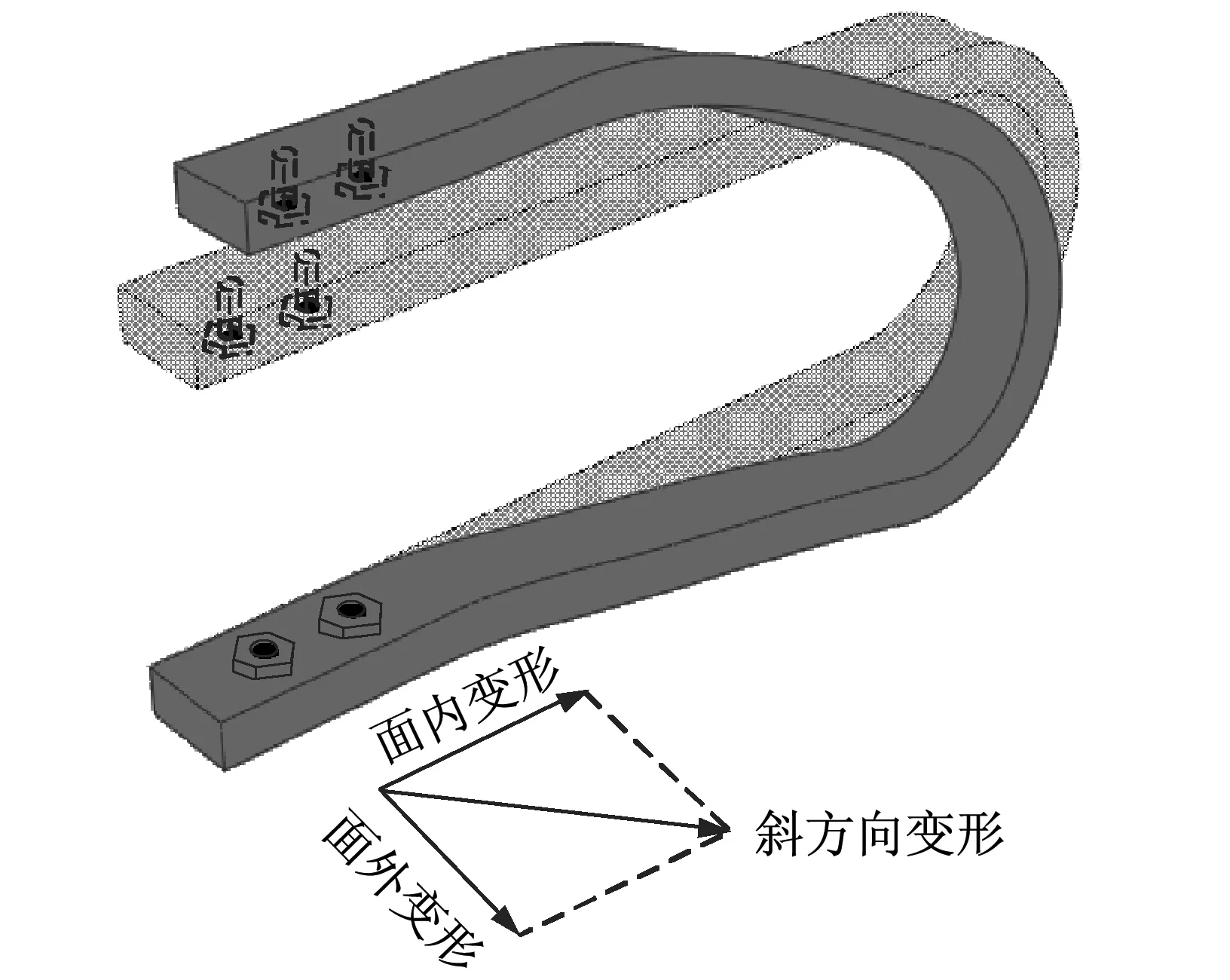
(c) 斜方向变形

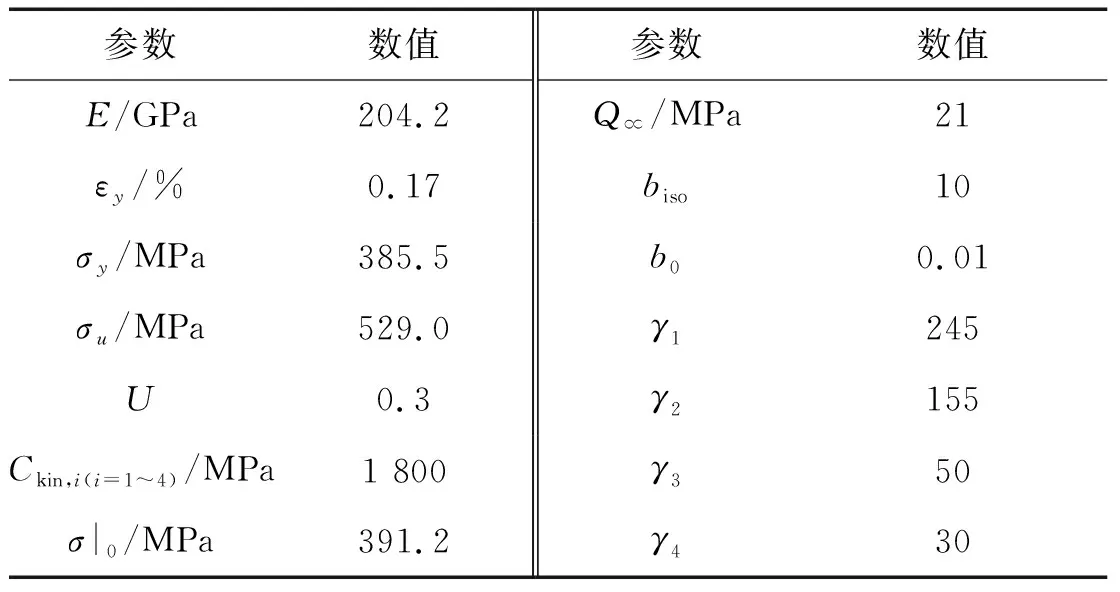
表2 Q345qC钢材的力学性能

为了分析阻尼元件在斜方向的变形性能，图8(b)中对直接在斜方向施加强制位移后分析得到的曲线与在x、y方向分别施加强制位移后合成到该方向上得到的曲线进行对比。由上述曲线结果可知，U型钢阻尼元件在不同方向变形作用下的力学特性差异显著，且由于非线性力学特性的影响，阻尼元件任一方向的荷载-位移曲线无法通过其他方向合成得到。

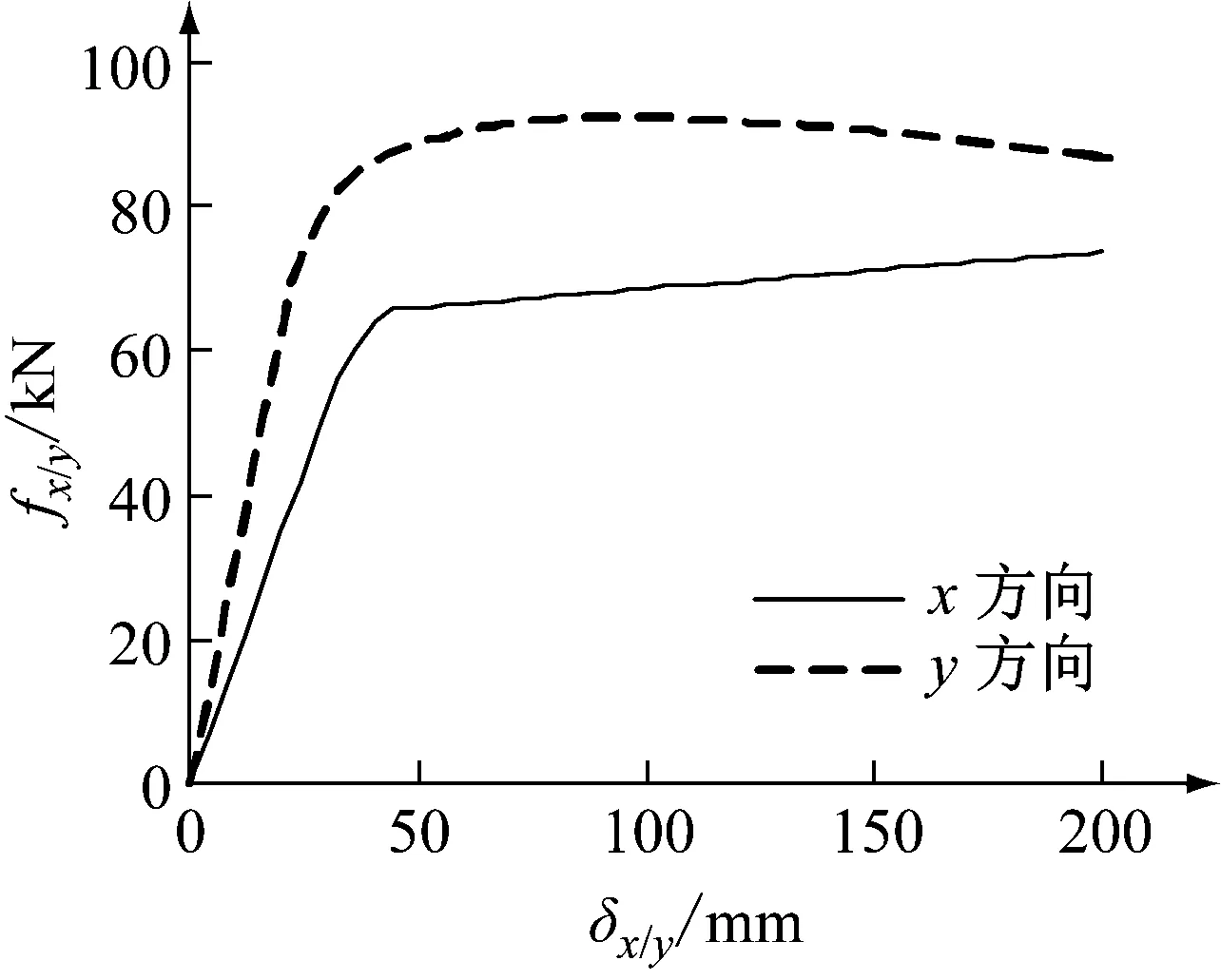
(a) x方向/y方向变形

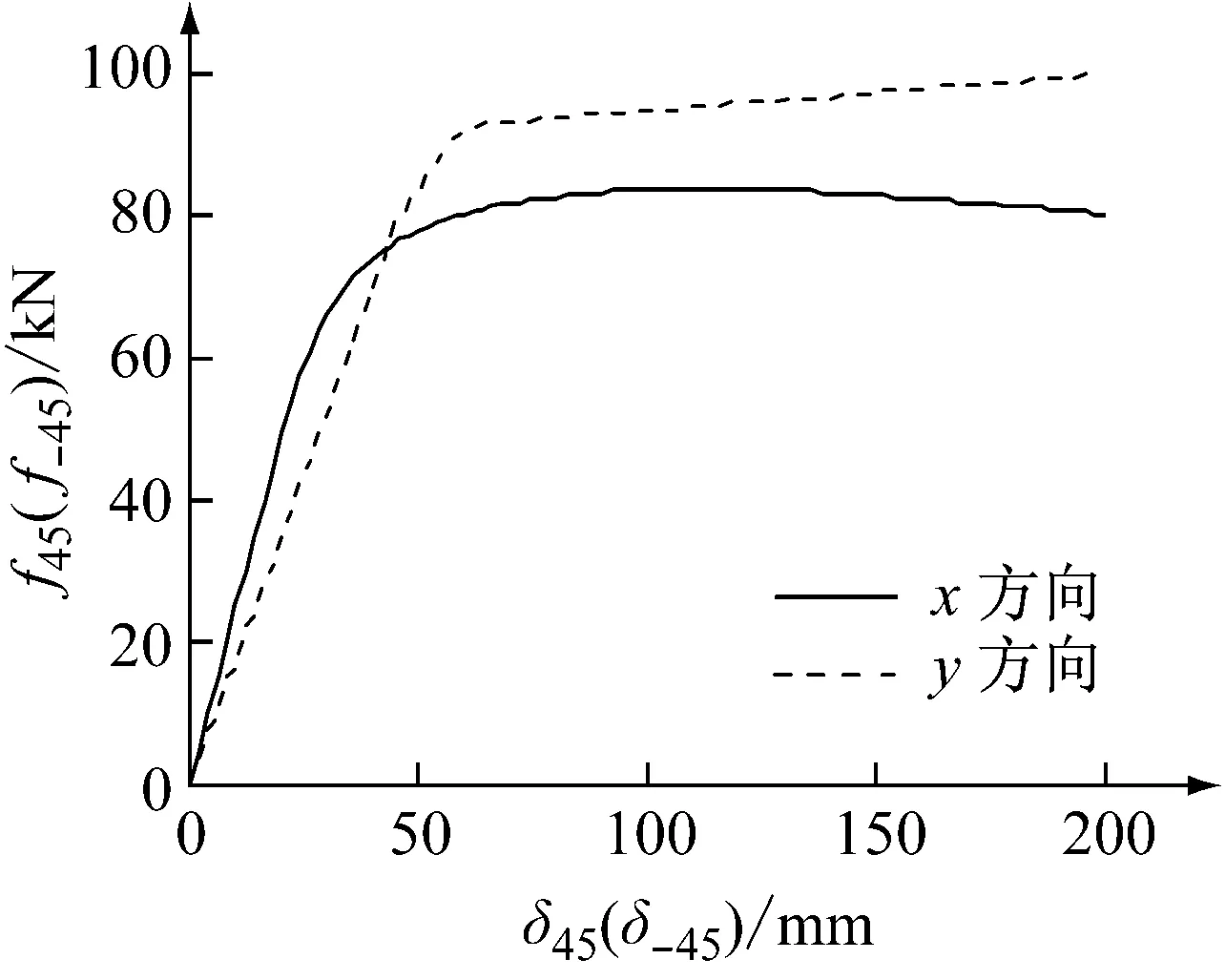
(b) 斜方向变形

2.2 参数确定

本文中，将U型钢阻尼元件的x、y、45°、-45°方向分别对应于MMSS模型的X、Y、45°、-45°方向(以下方向均用MMSS模型的方向标识)。在分析得到阻尼元件各方向的变形性能后，根据式(6)～(8)所示的弹簧基本力学参数确定方法可得到阻尼元件的各方向弹簧非线性特性值，如表3所示。

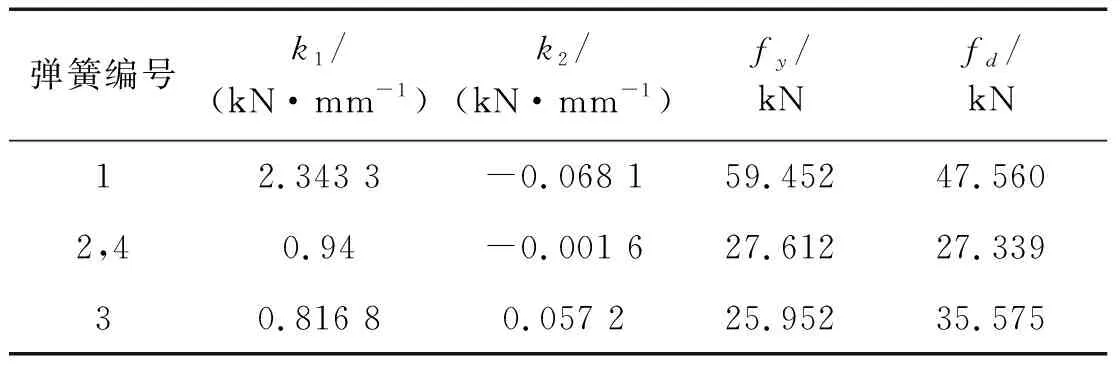
表3 弹簧非线性特性参数值

另一方面，基于式(9)所示的目标函数，利用图5所示的优化程序计算得到MMSS模型各弹簧的R0值分别为16.883、31.812、203.714、31.812，此时得到模型沿X、Y斜方向单向加载时的滞回曲线如图9所示。结果表明，MMSS模型的计算结果与目标曲线基本一致。

2.3 履历性能验证

本文选用单向循环位移、水平2方向规则循环位移以及随机位移3种加载形式，通过对U型钢阻尼元件的精细有限元模型分析结果与MMSS模型计算结果进行对比，以此来检验由上述方法确定的MMSS模型是否能够准确地模拟U型钢阻尼元件的履历性能。

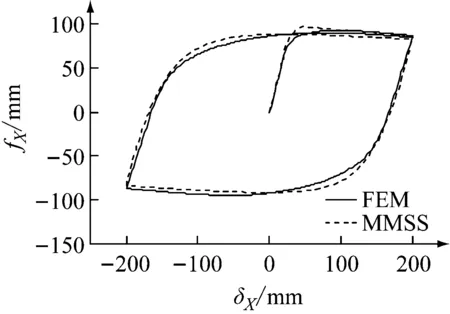
(a) X方向

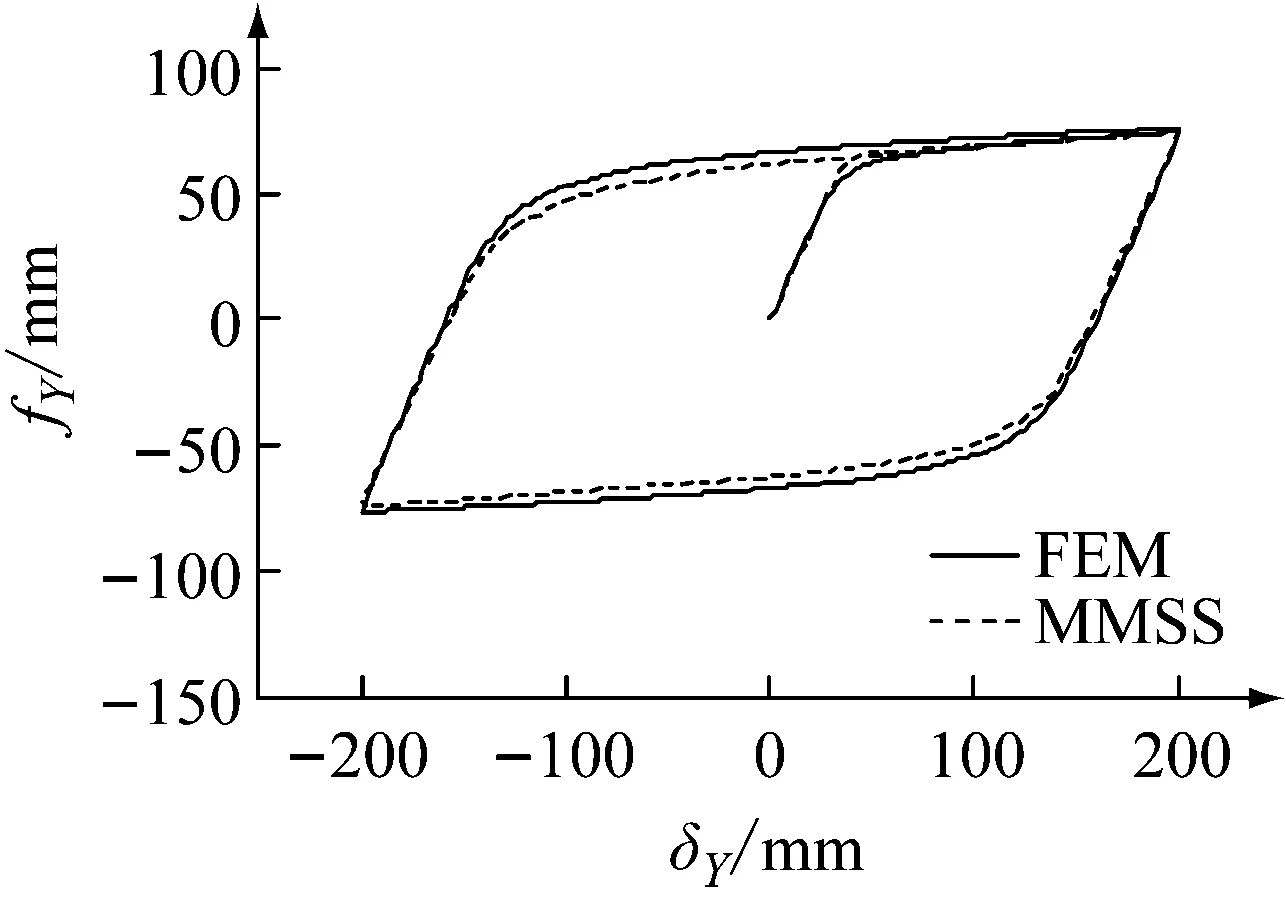
(b) Y方向

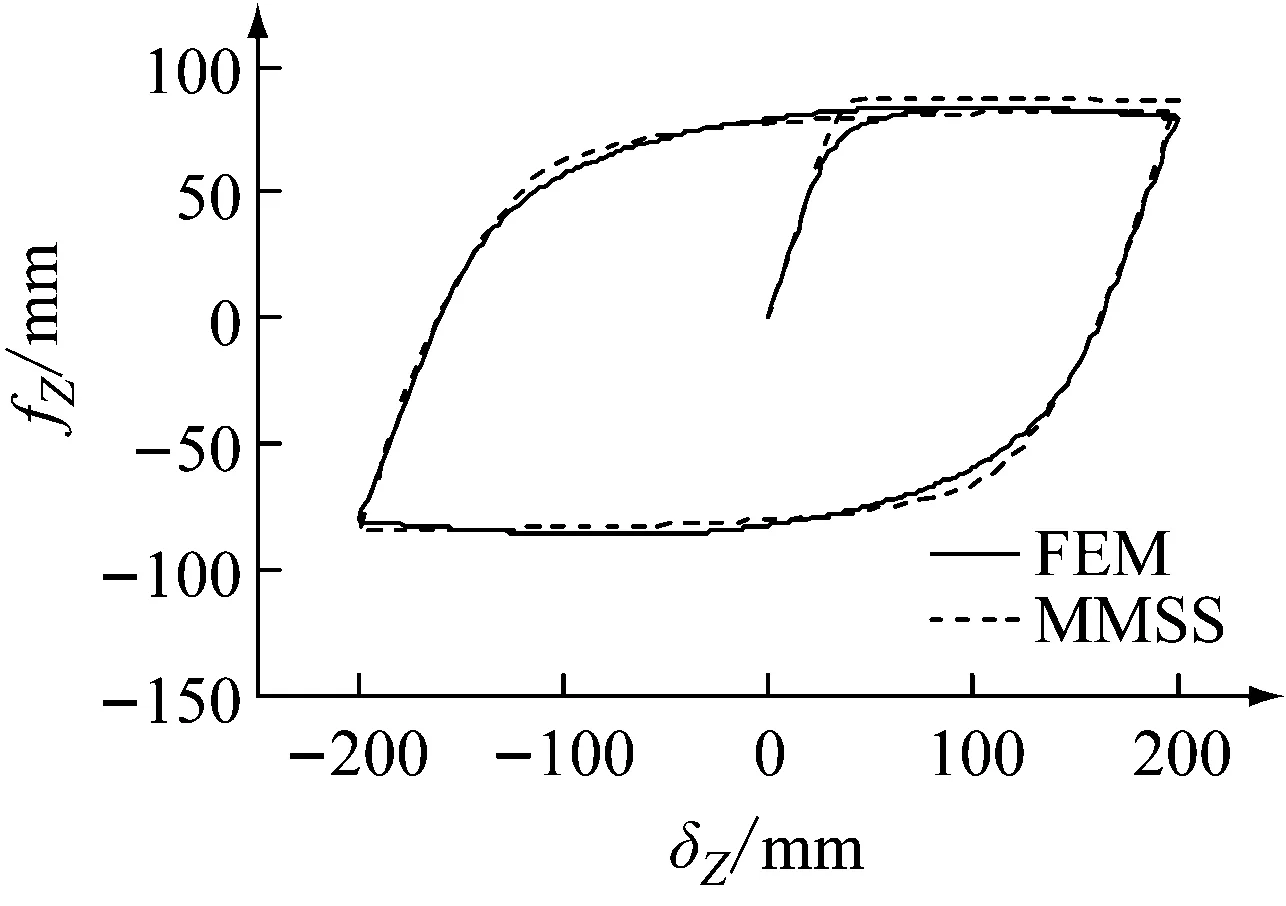
(c) 斜方向

2.3.1 单向循环位移

本文按图10所示的加载制度对阻尼元件按X、Y、22.5°、45°以及67.5°方向5个方向进行单向循环加载，图11为两种模型在对应方向的滞回曲线比较结果。结果表明，在单向循环位移加载条件下，MMSS模型能精确地模拟出钢阻尼器不同方向变形的滞回特性。

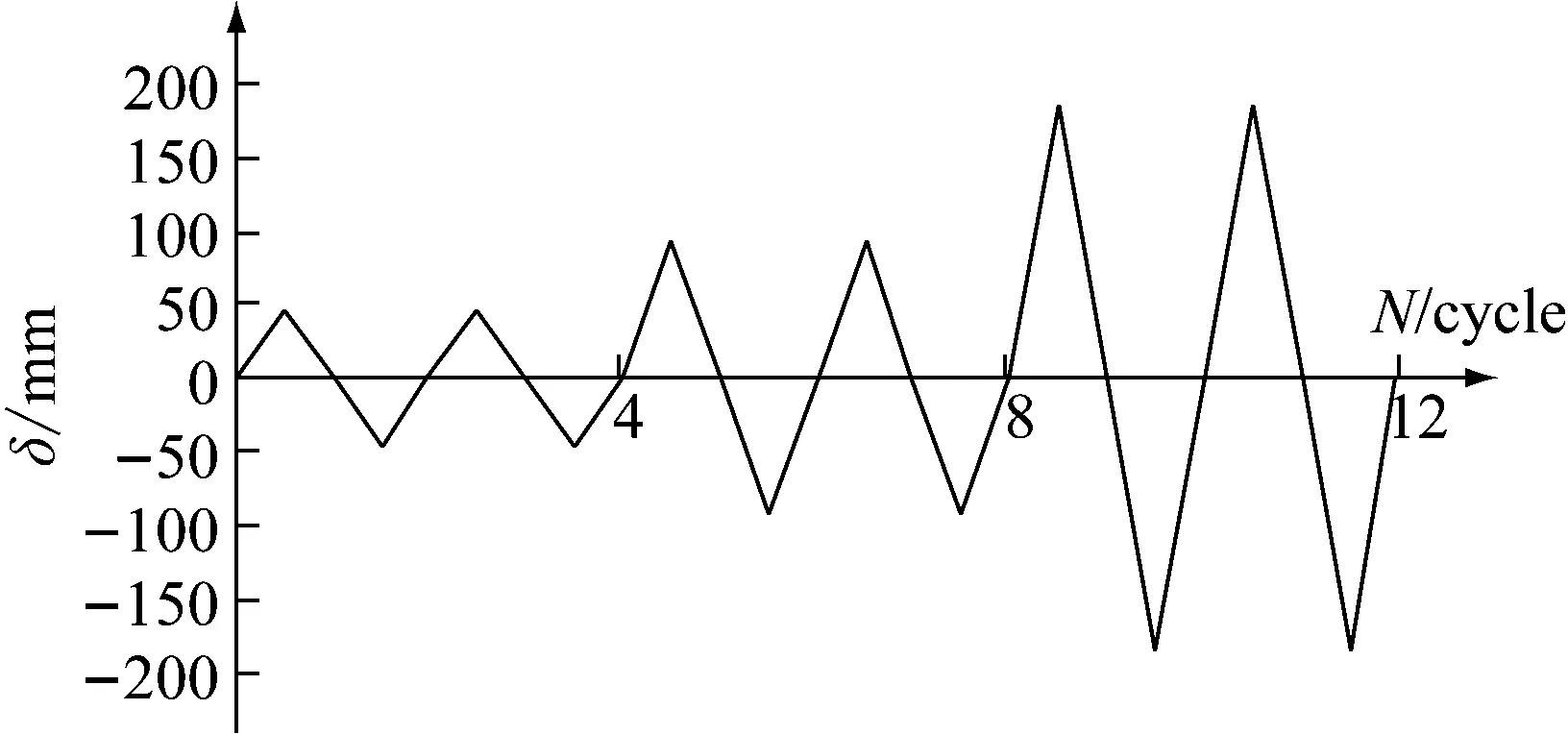
图10 单向循环位移加载制度

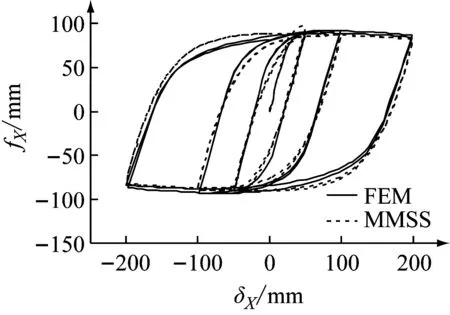
(a) X方向

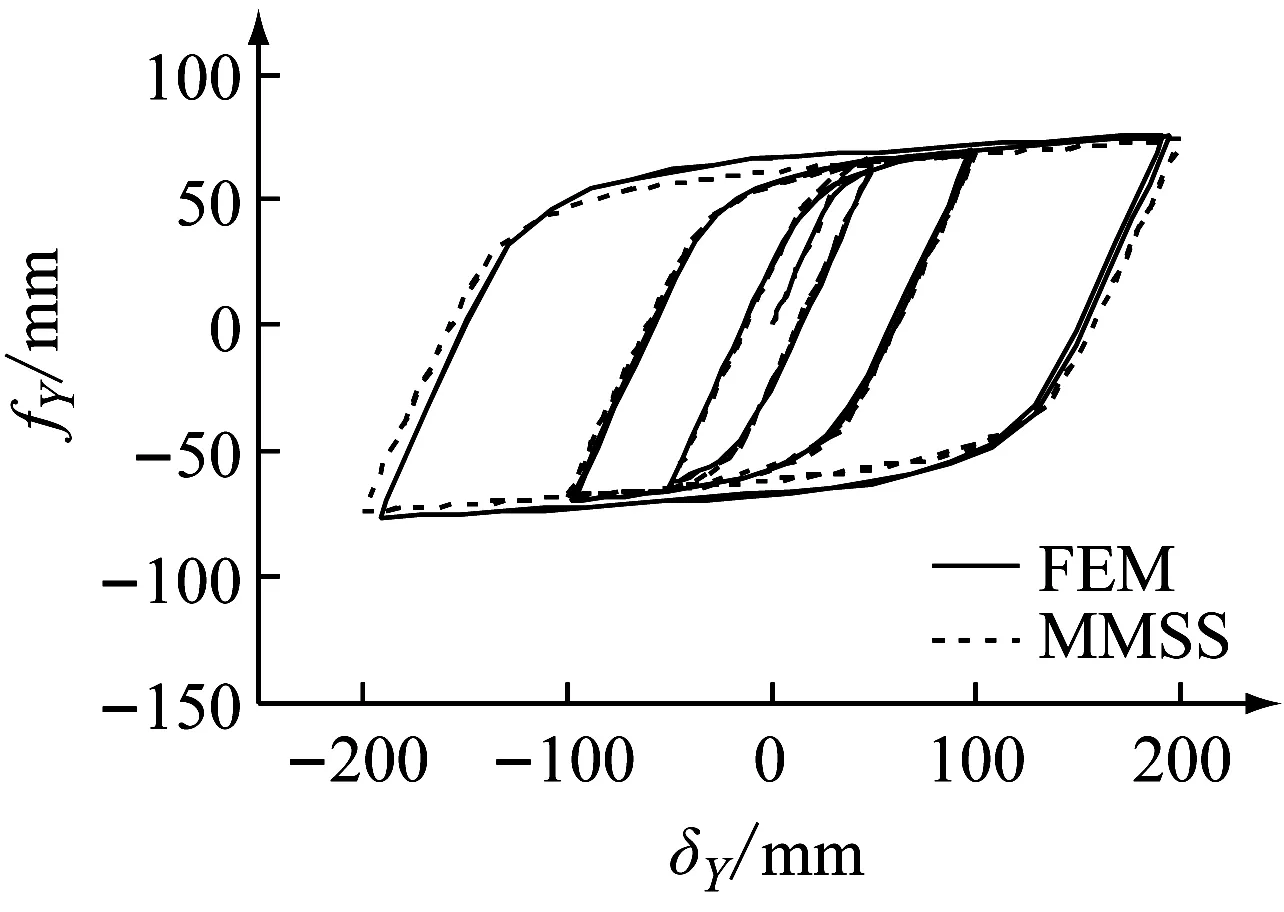
(b) Y方向

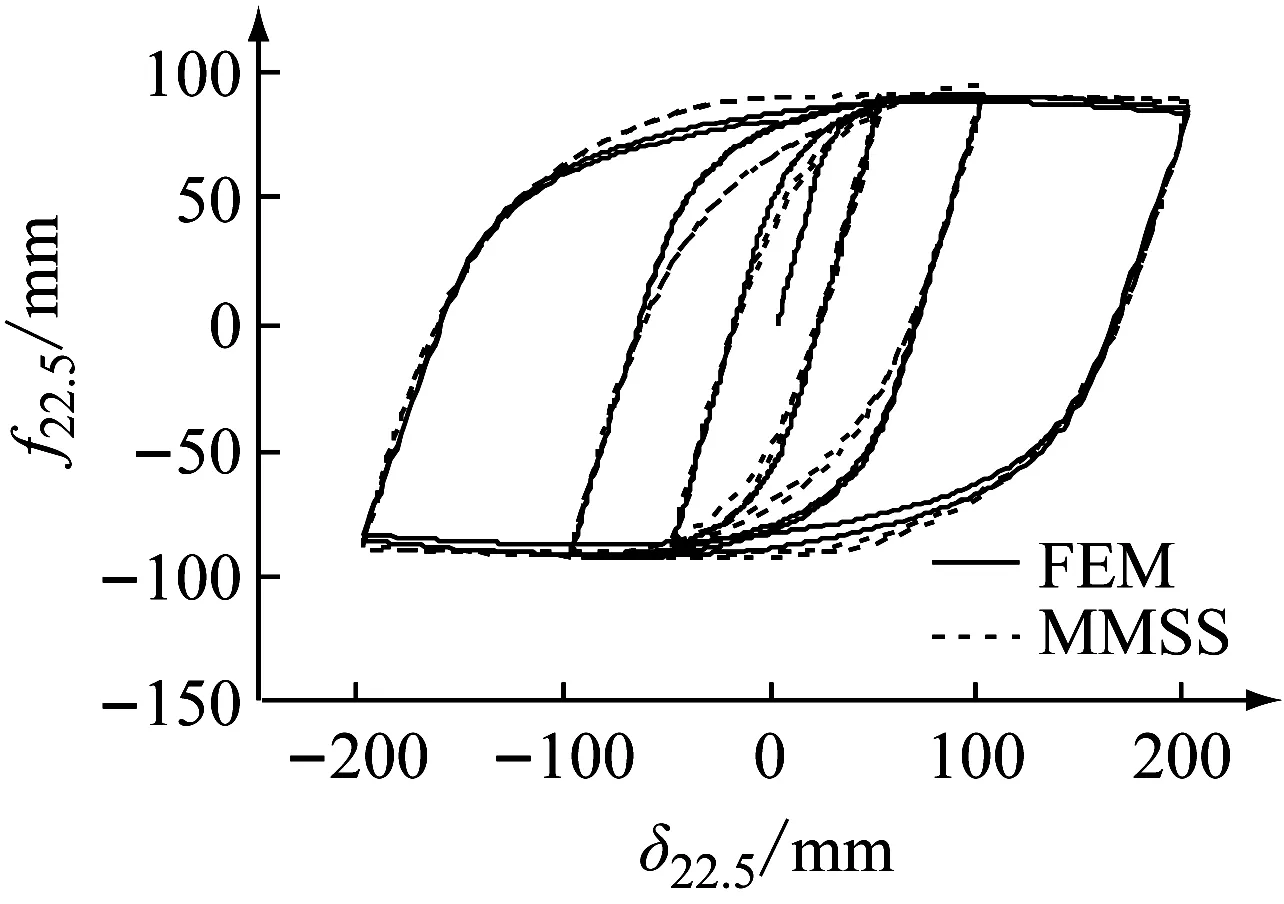
(c) 22.5°方向

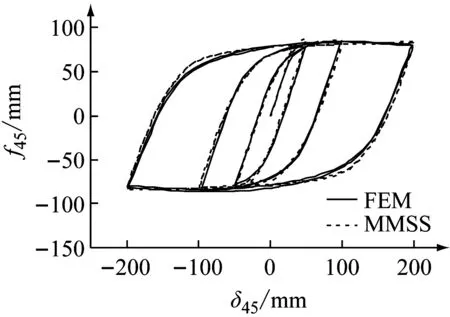
(d) 45°方向

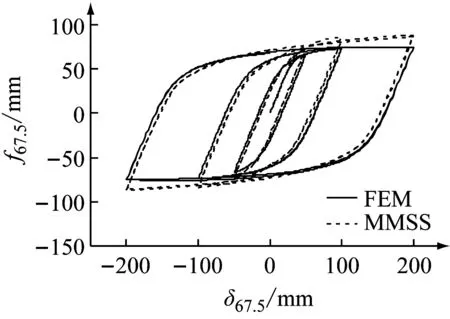
(e) 67.5°方向

2.3.2 水平2方向规则循环位移

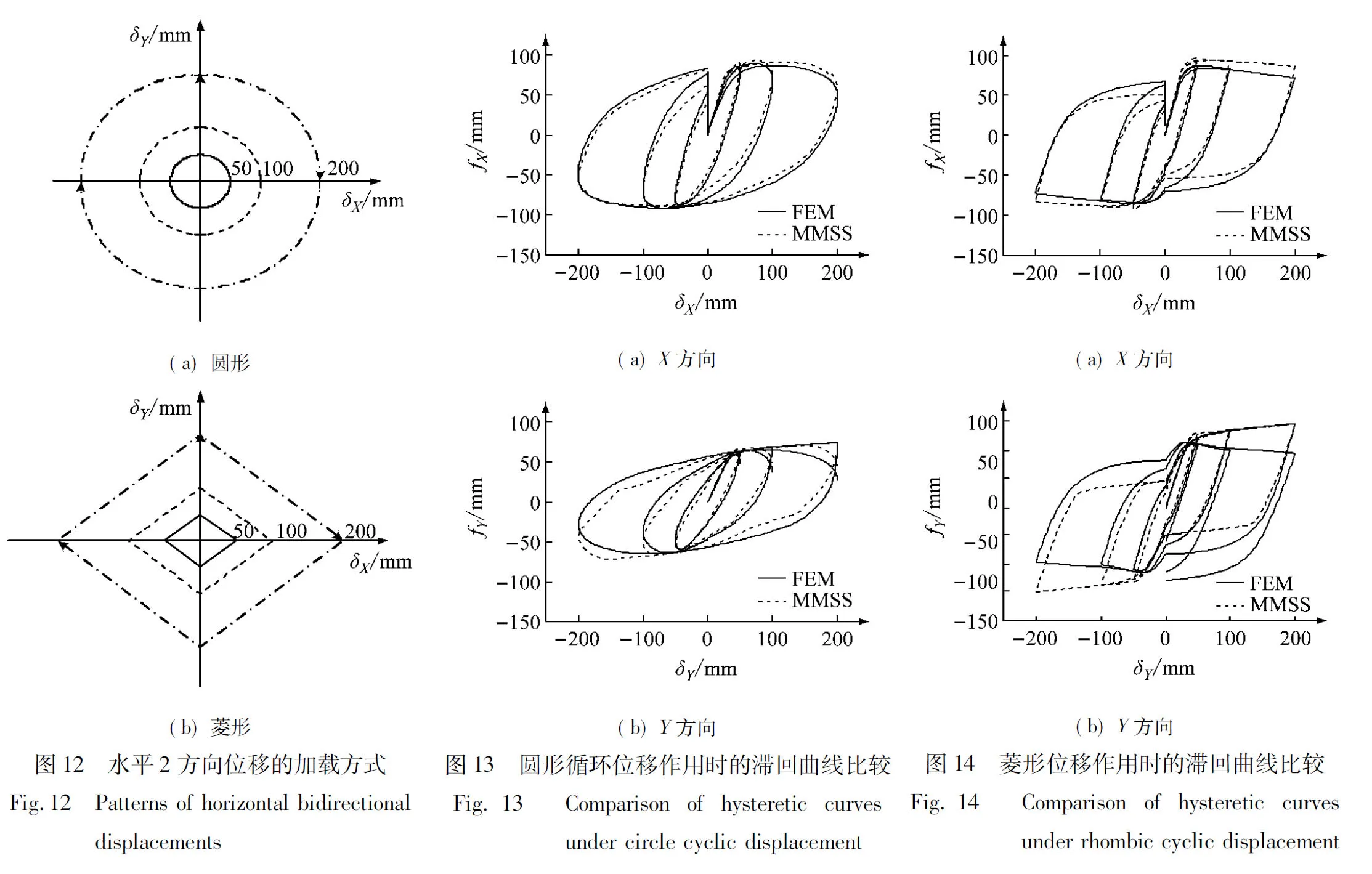
本文通过圆形和菱形两种不同形式的水平2方向规则循环位移的分析计算来进一步验证MMSS模型的有效性，具体加载方式，如图12所示。图13和图14为两种模型的滞回曲线比较结果。结果表明，MMSS模型总体上能较准确地模拟U型钢阻尼元件按圆形及菱形循环变形时的滞回性能，但与单一方向的变形相比，计算精度略有下降。

2.3.3 随机位移

实际中，地震荷载对阻尼装置的作用是非规则变化的。因此，本文通过加载如图15所示A、B两种不同形式的随机位移以验证MMSS模型在结构地震反应计算分析中的有效性。

图16和图17为两种模型在随机位移下滞回曲线的比较结果。结果表明，MMSS模型能较好地模拟出U型钢阻尼元件在A、B两种位移规律不同的随机位移下的滞回性能，说明MMSS模型具有良好的实用性。

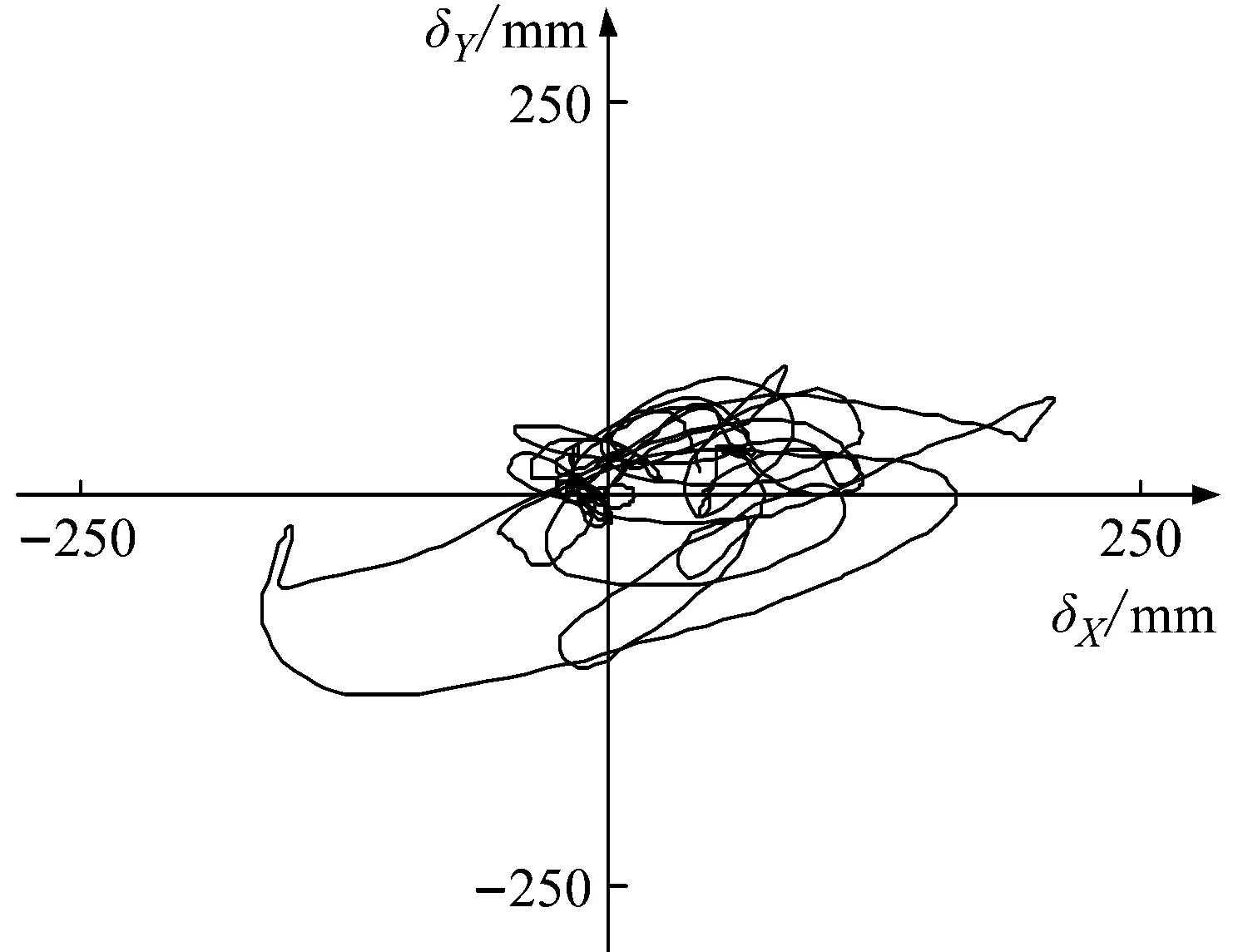
(a) 随机位移A

(b) 随机位移B

3 结 论

为了建立钢阻尼器考虑水平2方向变形的简化滞回模型，本文提出一种MMSS模型，并以建筑物和桥梁结构减隔震设计中常见的U型钢阻尼元件为例，验证了该模型的有效性。主要得到以下几点结论：

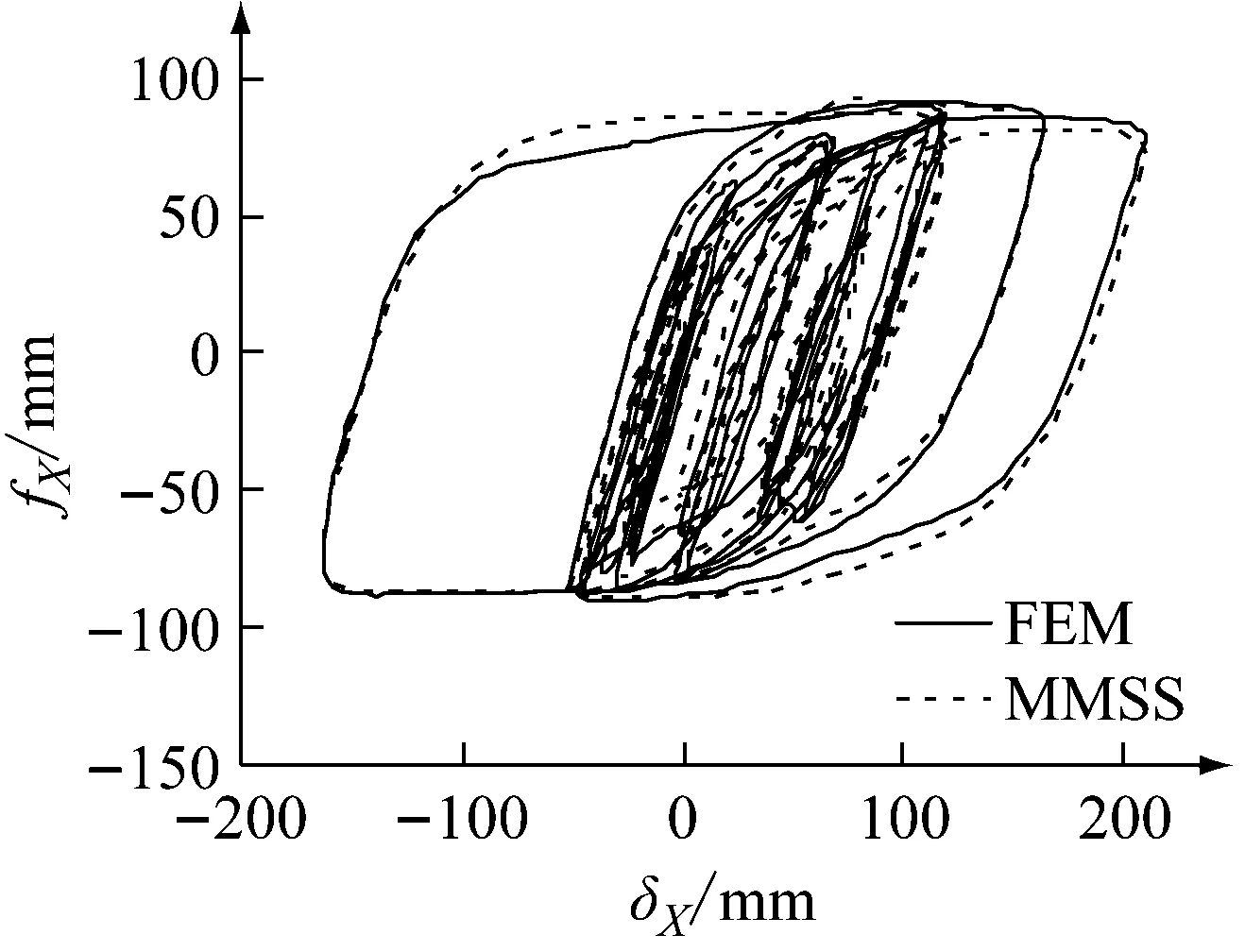
(a) X方向

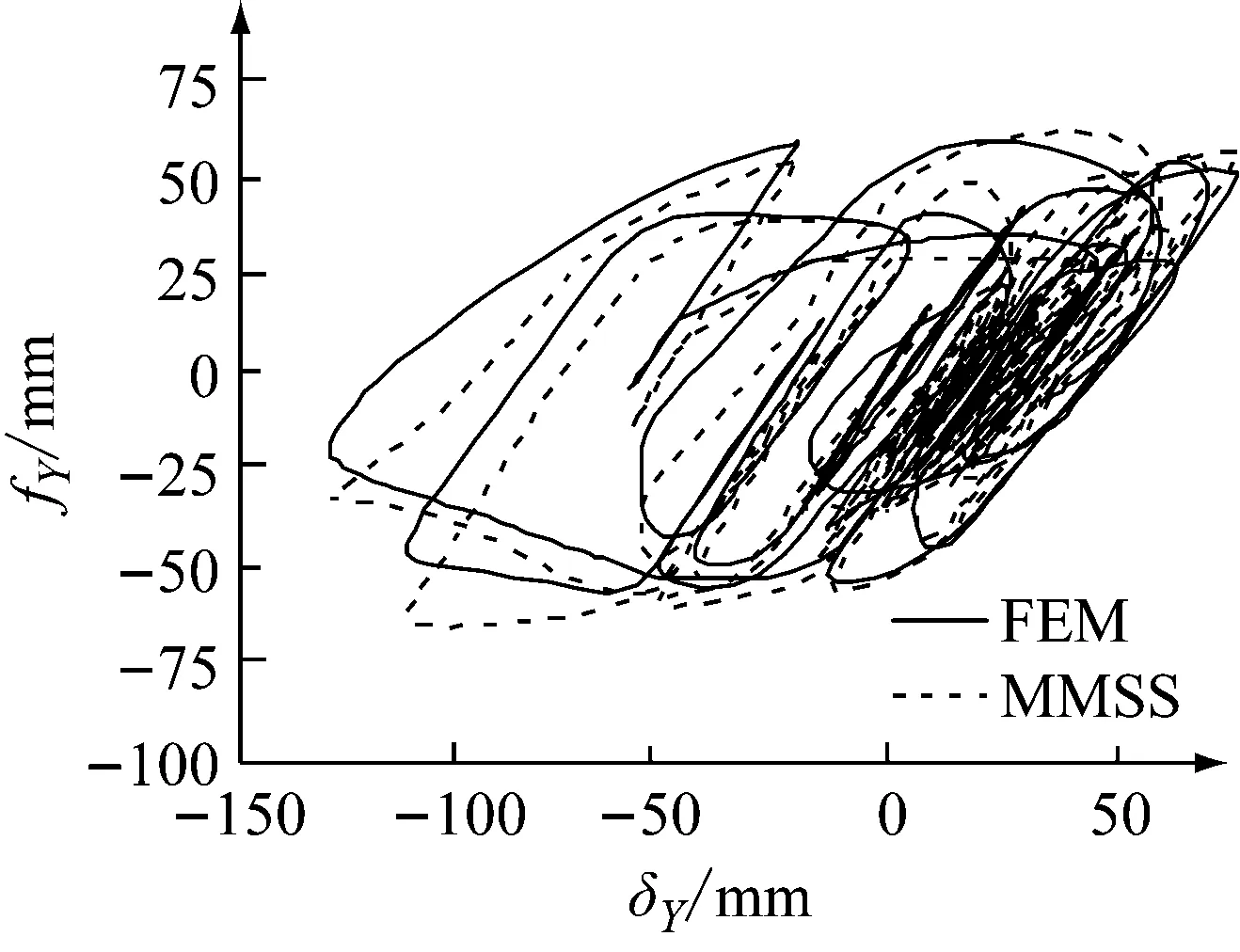
(b) Y方向

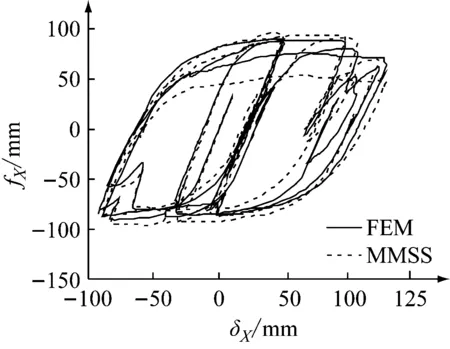
(a) X方向

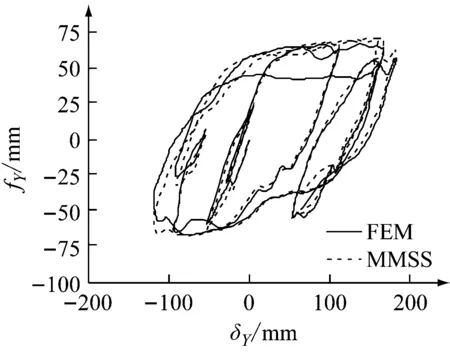
(b) Y方向

(1) 钢阻尼器在不同方向位移作用下的力学特性存在显著差异，且其在任一方向上的滞回性能不能通过其他方向合成得到。为了能准确地模拟阻尼器的变形性能，需要采用具有多方向异性特征的简化滞回模型。

(2) 根据多方向等刚度、等强度的原则提出MMSS模型中各弹簧的初始刚度、屈服点以及屈服后刚度的计算方法；通过优化算法确定MP模型的形状参数。算例结果表明，上述方式不仅具有可操作性，且计算精度较好。

(3) MMSS模型可以较准确地模拟钢阻尼元件在水平2方向变形时的力学性能，为采用钢阻尼器的地震反应分析提供了一种简便的计算方法。