一个新的超大范围混沌系统及其自适应滑模控制

徐昌彪， 钟 德， 夏 诚， 黎 周

(1.重庆邮电大学 光电工程学院，重庆 400065； 2.重庆邮电大学 通信与信息工程学院，重庆 400065)

混沌是确定性系统的内在随机性，是非线性动力学系统所特有的一种形式，并且广泛地存在于自然界诸如物理[1]、化学[2]、地质学[3]以及生物学[4]等领域。自从1963年Lorenz[5]在三维自治系统中发现了第一个混沌吸引子以来，人们不断地发现新的混沌系统，如Chen等[6]系统、Lü等[7]系统、Chua等[8]系统、Liu等[9]系统等。但大多数混沌系统的参数变化范围较小[10-14]，它们的混沌特性受到系统任意一个参数很大影响，参数的变更与误差会改变系统的动力学行为，使得系统相轨收敛于不动点，或是处于周期、拟周期甚至混沌振荡状态等。而具有超大范围混沌系统的混沌特性在某个参数的变动下始终处于混沌状态，其最大Lyapunov指数始终大于零，这使得该系统具有更丰富的动力学特性，在混沌雷达[15]，激光振荡[16]以及信息处理[17]等领域中具有重大的应用价值。

但总的来说，关于超大范围混沌系统的研究还处于起步阶段，Liu等[18]提出了一个具有较大参数范围的新型三维混沌系统，参数范围为[-100，100]。贾红艳等[19]在已有的超混沌系统研究的基础上提出了一个大范围超混沌系统，参数范围为[10，1 000]，梅蓉等[20]构建了一类新的超大范围超混沌系统，参数范围为[0，105]，但仿真只在[0，2 000]进行。

基于以上研究，本文提出了一个超大范围的混沌系统，其中参数b的取值为[0，107]，比本文中提到的其他系统的参数范围都要大。理论分析了系统的动力学特性，进行了数值仿真和电路仿真。设计了一个自适应控制器和一个自适应滑模控制器，分别用于具有未知参数混沌系统的全局稳定和给定信号的追踪与未知参数的辨识。仿真结果表明了所设计控制器的可行性和有效性。

1 新混沌系统模型与基本特性

1.1 新混沌系统模型

新混沌系统的数学模型为

(1)

式中：x，y，z为系统变量。取a=3，b=10，初值为[1，1，1]时，系统存在一个典型的吸引子，如图1所示。此时系统的三个Lyapunov指数为0.122 7，-0.001 7，-3.121 0。

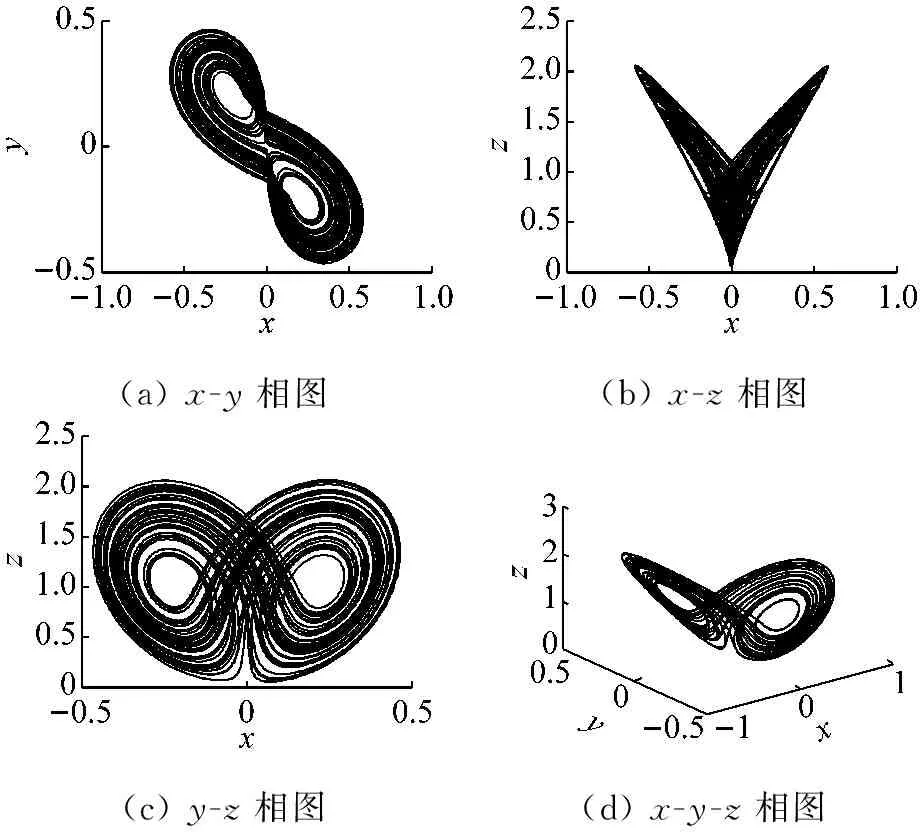
(a) x-y相图(b) x-z相图(c) y-z相图(d) x-y-z相图

图1 系统相图

Fig.1 Phase diagram of the system

1.2 对称性和不变性

系统在变换(x,y,z)→(-x,-y,z)下具有不变性，即系统关于z轴对称，且这种对称性对所有系统参数均成立。

1.3 耗散性和吸引子的存在性

根据式(1)，有

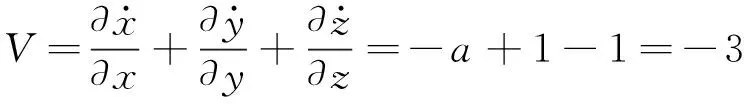
(2)

可见系统是耗散的，则系统的轨线最终会被限制在一个体积为0的极限点集上，并且它的渐近动力学行为会被固定在一个吸引子上，这说明了吸引子的存在性。

1.4 平衡点及稳定性

令式(1)的左边等于0，即

(3)

其中a=3，b=10时，系统有3个平衡点，分别为：

S1=(0,0,0)，

S2=(-0.223 6,0.223 6,1)，

S3=(0.223 6,-0.223 6,1)。

在平衡点S1=(0,0,0)处线性化系统，得其Jacobi矩阵为

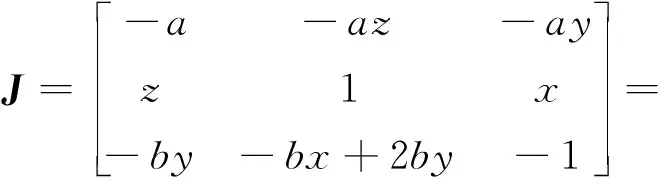
(4)

特征值方程为

|λI-J|=0

(5)

计算出特征值为λ1=-3，λ2=1，λ3=-1。由于特征值λ1和λ3是负实数，λ2是正实数，故平衡点S1是不稳定的鞍点。

同理，在平衡点S2和S3处分别线性化系统，得到它们的特征值均为λ1=-3.434 8，λ2=0.217 4+1.856 4i，λ3=0.217 4-1.856 4i。由于特征值λ1是负实数,λ2和λ3均有正实部，故平衡点S2和S3都是不稳定的鞍点。

1.5 时域波形图、频谱图以及Poincare截面图

取a=3，b=10，初值为[1，1，1], 采用四阶龙格-库塔(ODE45)算法对式(1)进行求解，可得系统状态变量x的时域波形图，如图2所示，可以看出系统为非周期系统。如图3所示，系统的功率谱是连续谱，没有明显的波峰，并且峰值连成一片，说明了系统是混沌系统。选取的Poincare截面如图4所示，可以看出Poincare截面上有一些成片的具有分形结构的密集点，吸引子的叶片清晰可见，也表明了系统具有混沌特性。

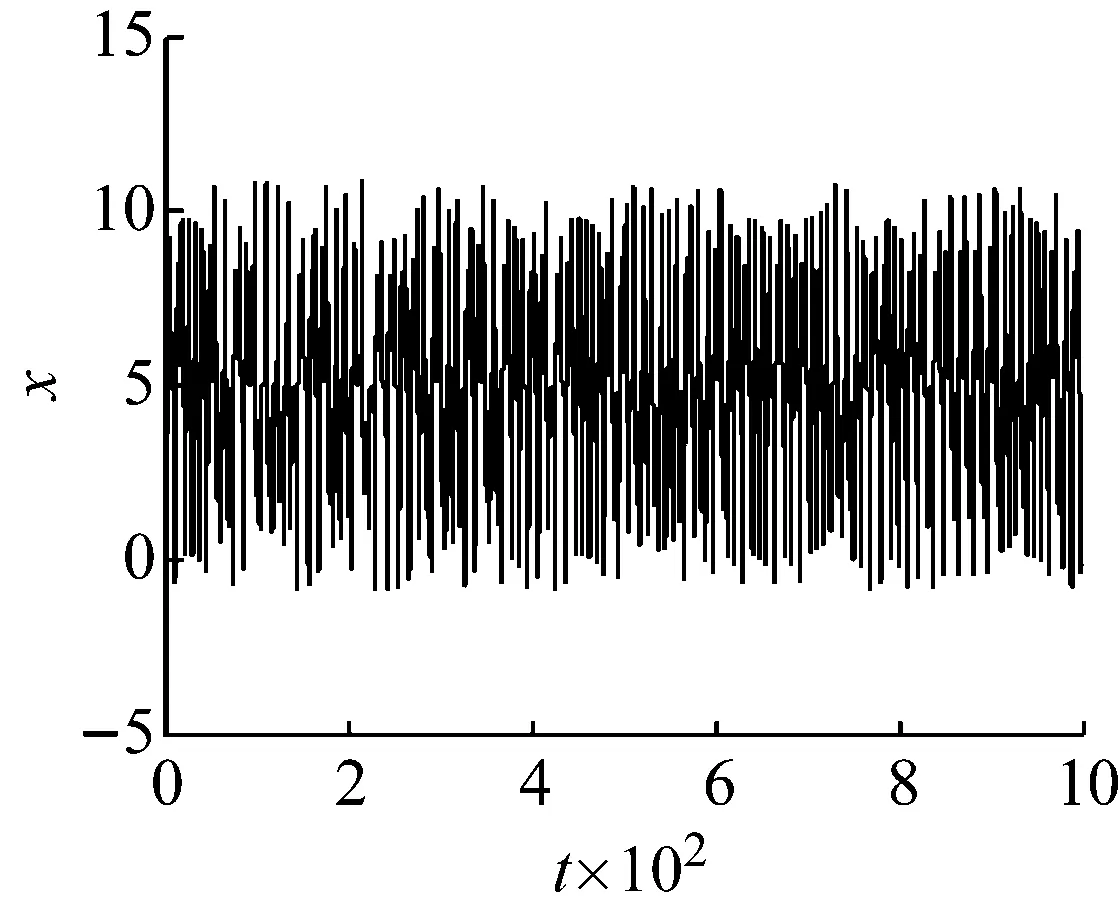
图2 状态变量的时域波形

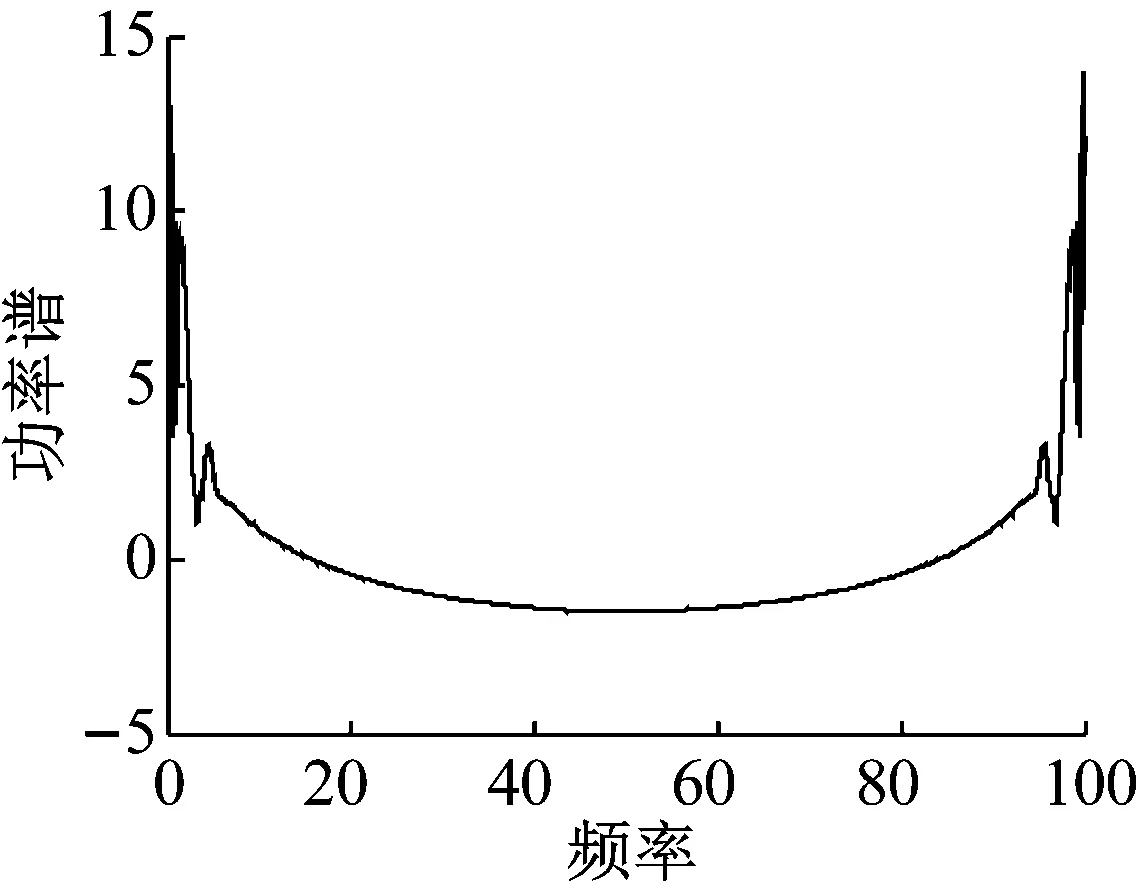
图3 系统的功率谱

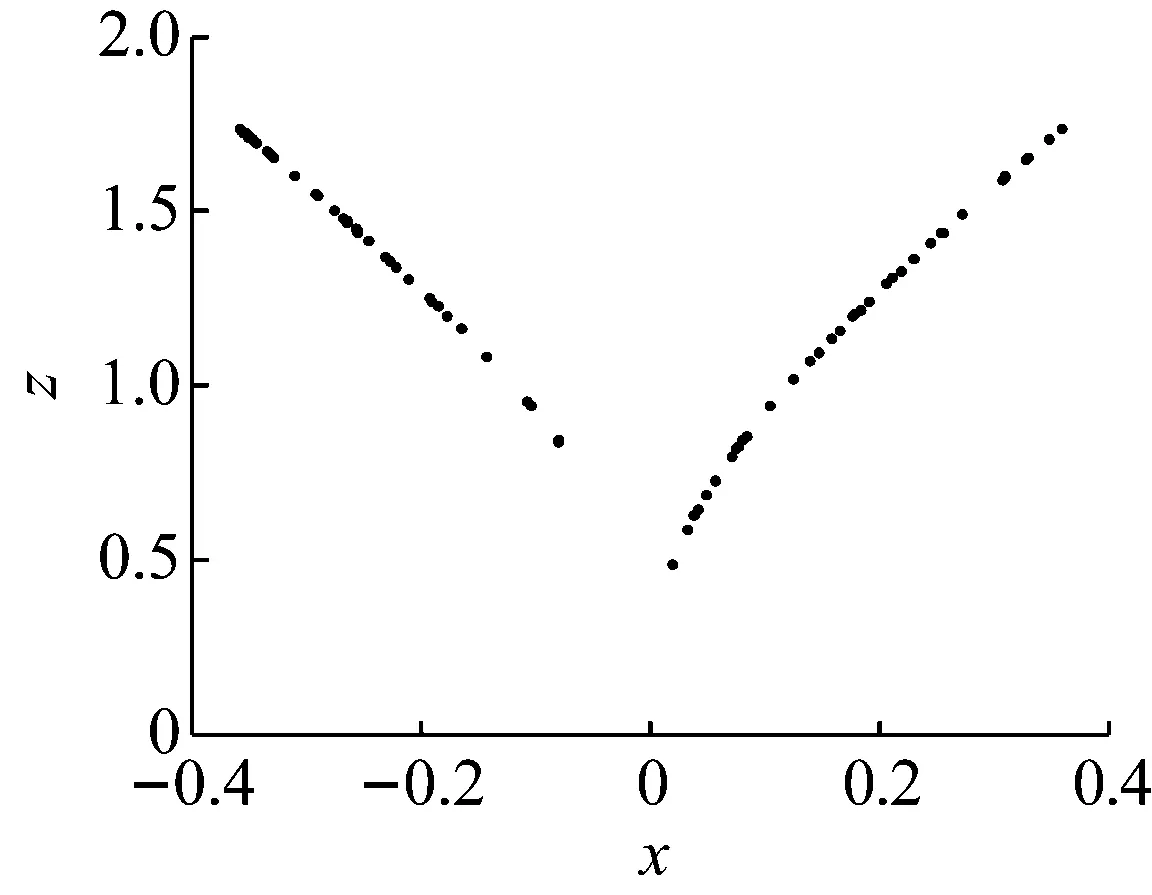
图4 系统的Poincare截面：y=0

1.6 Lyapunov指数和Lyapunov维数

采用Jacobi法计算出系统的Lyapunov指数谱如图5所示，在参数b从0～107变化时，系统的三个Lyapunov指数都趋于固定常数，为恒Lyapunov指数谱。图6为系统变量y随参数b从0～107变化时的分岔图，可以看出系统都处于混沌状态。

系统的Lyapunov维数为：

(6)

当a=3，b=10时，系统的三个Lyapunov指数分别为L1=0.122 7，L2=-0.001 7，L3=-3.121 0，故可计算出DL=2.038 8。由此可见，系统的Lyapunov维数为分数维数，验证了系统为混沌系统。

2 系统的电路仿真

采用线性电阻、电容、LM2924N运算放大器、MULTIPLIER模拟乘法器(乘法器的输出增益为0.1)，设计出系统的模拟电子电路，如图7所示。

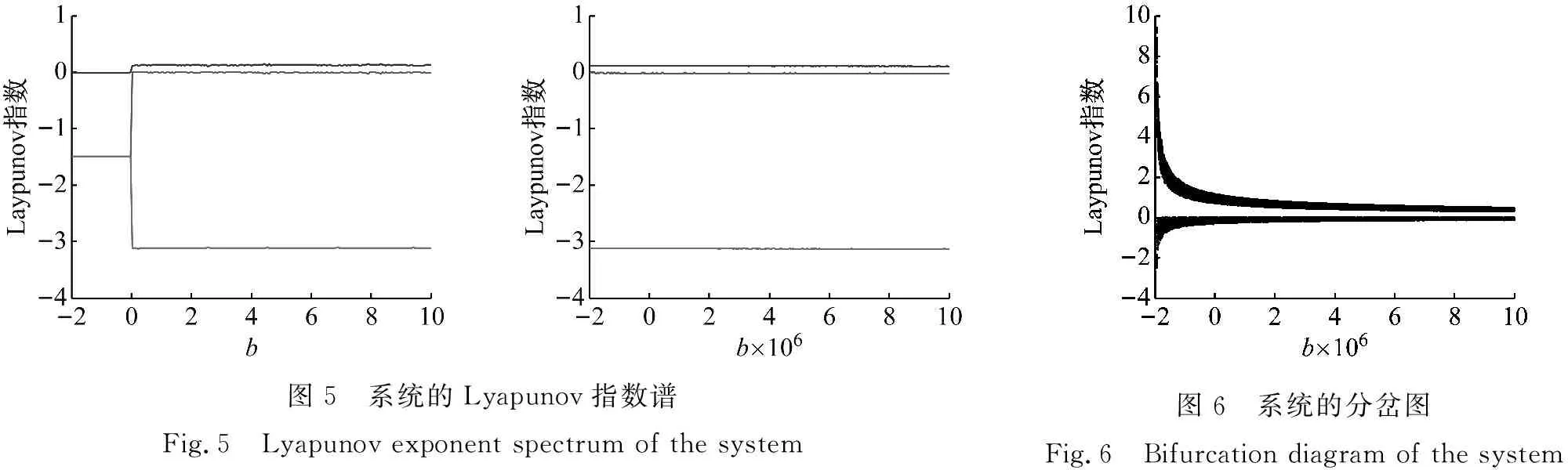
图5 系统的Lyapunov指数谱Fig.5 Lyapunov exponent spectrum of the system图6 系统的分岔图Fig.6 Bifurcation diagram of the system

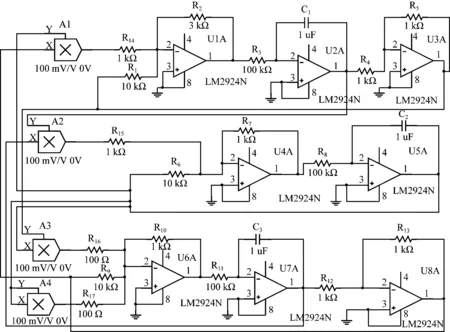
图7 电路原理图

根据系统参数以及电路理论，由乘法器的输出增益为0.1，得电路方程为：

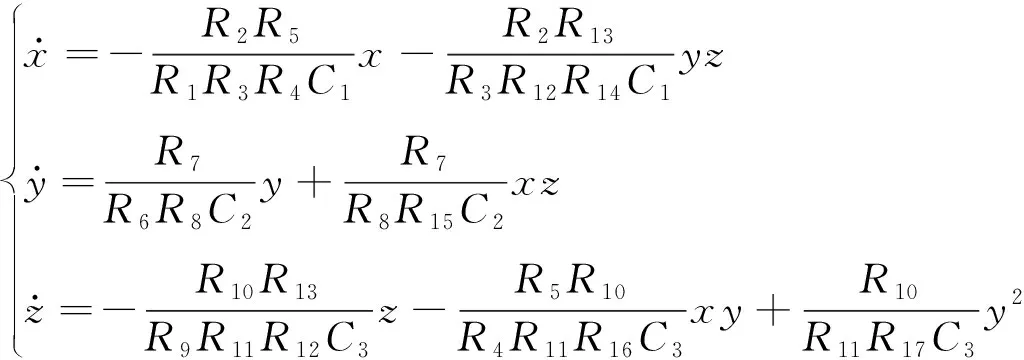
(7)

当取R1=R6=R9=10 kΩ，R3=R8=R11=100 kΩ，R2=3 kΩ，R4=R5=R7=R10=R12=R13=R14=R15=1 kΩ，R16=R17=0.1 kΩ，C1=C2=C3=1 μF时，采用Multisim软件对电路进行了仿真实验，仿真结果如图8所示，可以看出仿真实验结果与数值仿真结果是一致的。

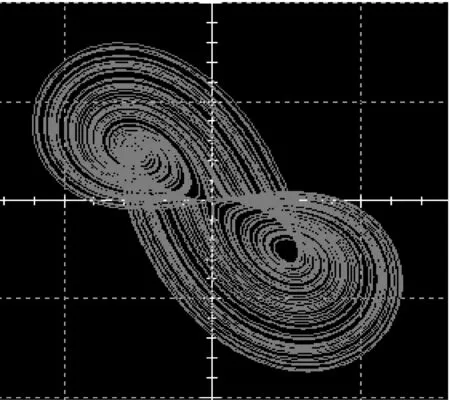
(a) x-y

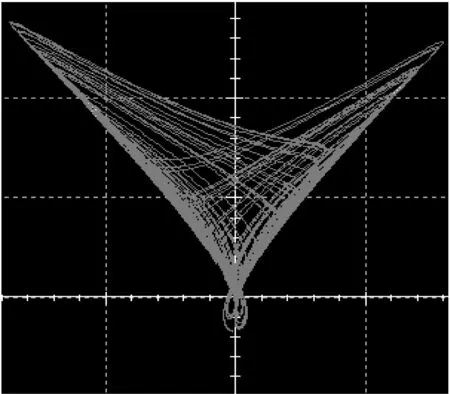
(b) x-z

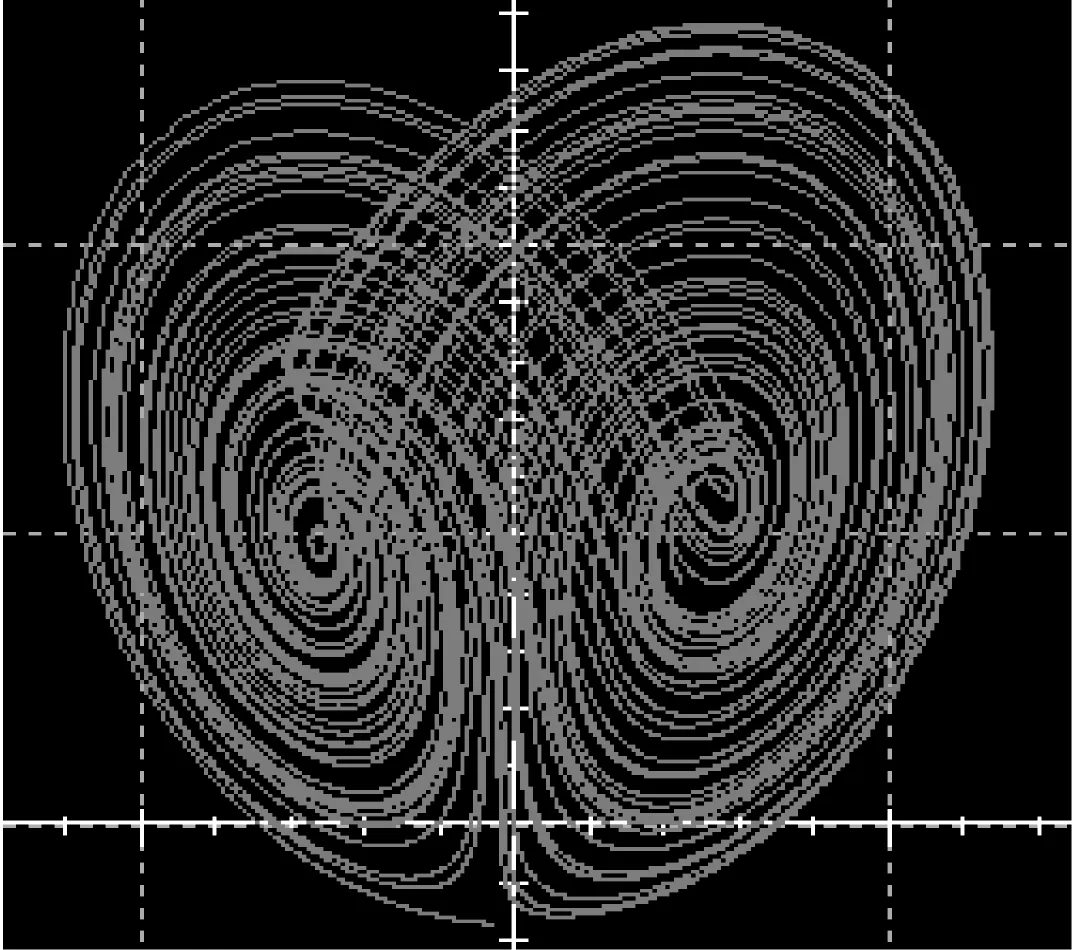
(c) y-z

3 参数未知的混沌系统的自适应控制

受控系统为

(8)

式中：x，y，z为系统变量，u1，u2，u3为自适应控制器。

设计自适应控制器为

(9)

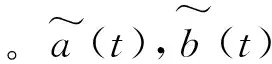
参数估计误差定义为

(10)

对式(8)求导，得

(11)

将式(9)和式(10)代入式(8)，得闭环系统

(12)

构造以下Lyapunov函数

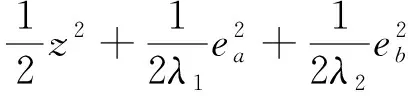
(13)

其中λ1，λ2均大于零，显然V是一个正定函数。对V求导可得

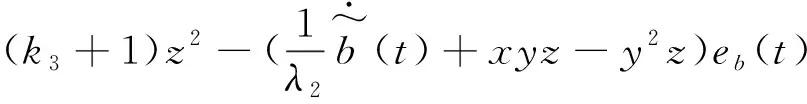
(14)

根据式(14)，设定参数更新定律如下

(15)

定理1具有未知参数的受控系统(8)通过自适应控制器(9)和参数更新定律(15)在所有初始条件下全局稳定，其中k1，k2，k3是正增益常数。

(16)

显然，式(16)是半负定的，状态变量x，y，z和参数估计误差ea(t)，eb(t)是全局有界的。

根据式(16)可得

(17)

因此，可得：

(18)

将不等式(18)两端从0到t积分，得到

(19)

根据式(19)可得x,y,z,ea,eb∈L2。

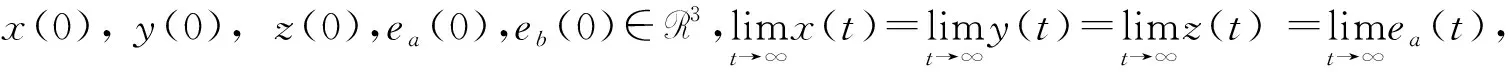
此外，由图9，10可知，在自适应控制器(9)和参数更新定律(15)的作用下受控系统(8)很快稳定到平衡点原点，并且实现了对系统未知参数的识别。

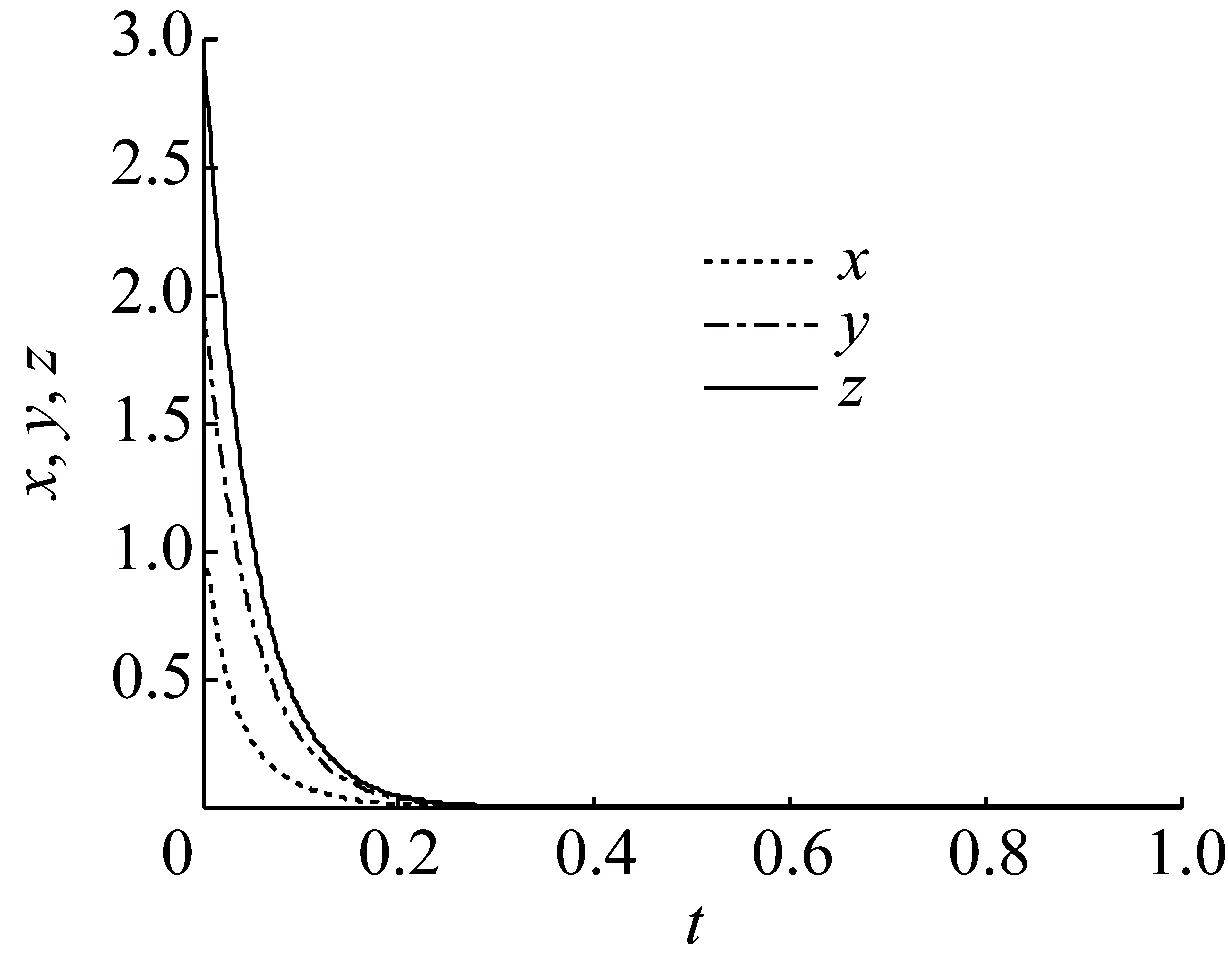
图9 受控状态x,y,z

4 参数未知的混沌系统的自适应滑模控制

考虑如下受控系统

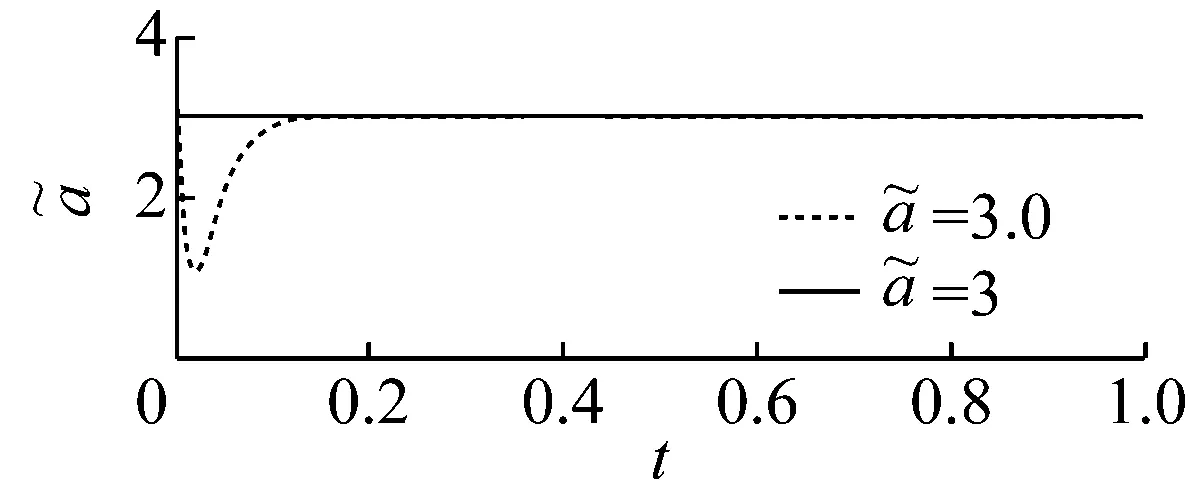
图10 参数和的收敛曲线

(20)

定义滑模函数

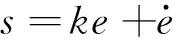
(21)

式中：r为理想位置信号，e=y-r为跟踪误差，k>0。

设计自适应控制器为

(22)

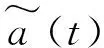
(23)

对参数估计误差(23)求导得到

(24)

定义Lyapunov函数为

(25)

对V求导，将式(22)和式(23)代入，得

(26)

取参数更新定律为

(27)

则

(28)

根据Lyapunov稳定性定理，可知受控系统式(20)的平衡状态是全局渐进稳定的。

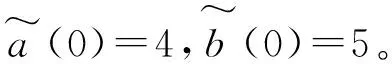
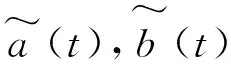
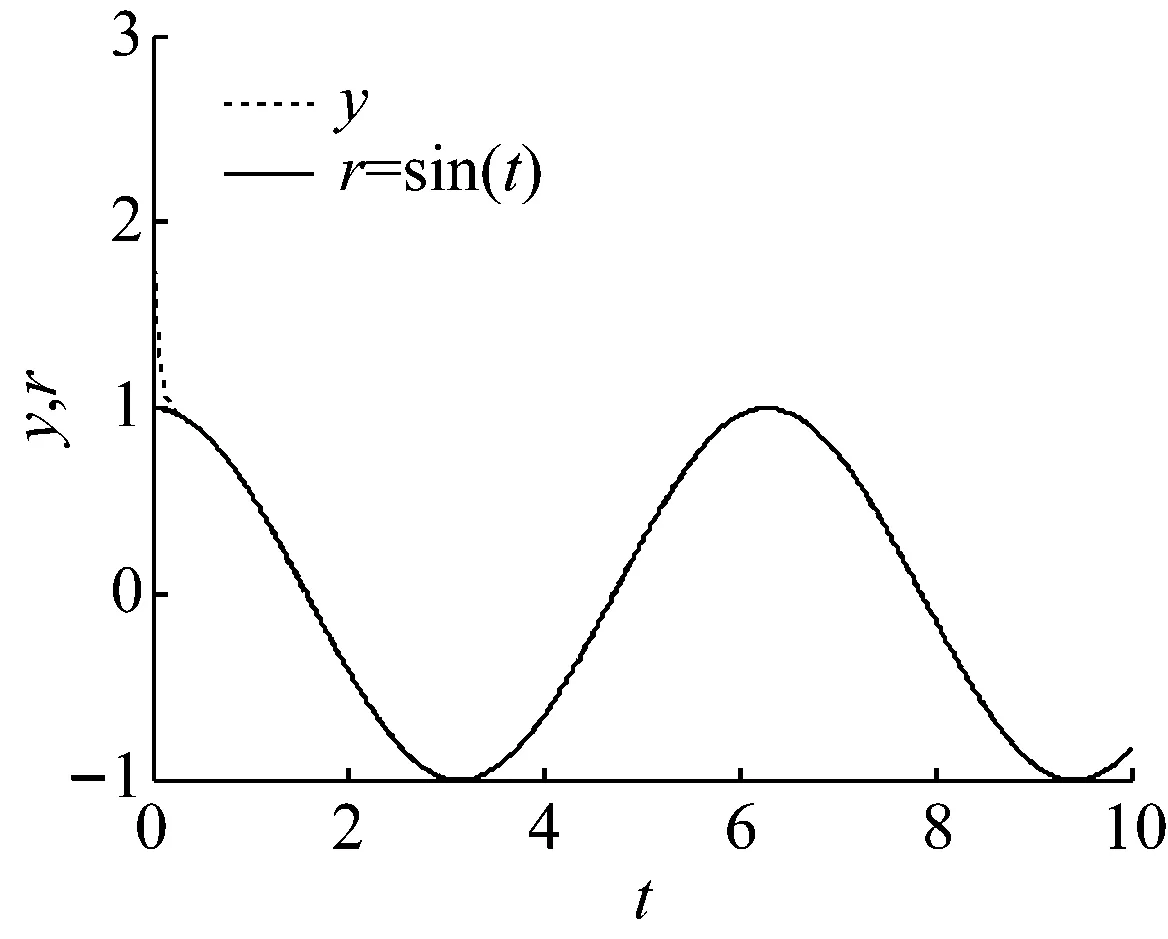
图11 跟踪sin(t)的曲线

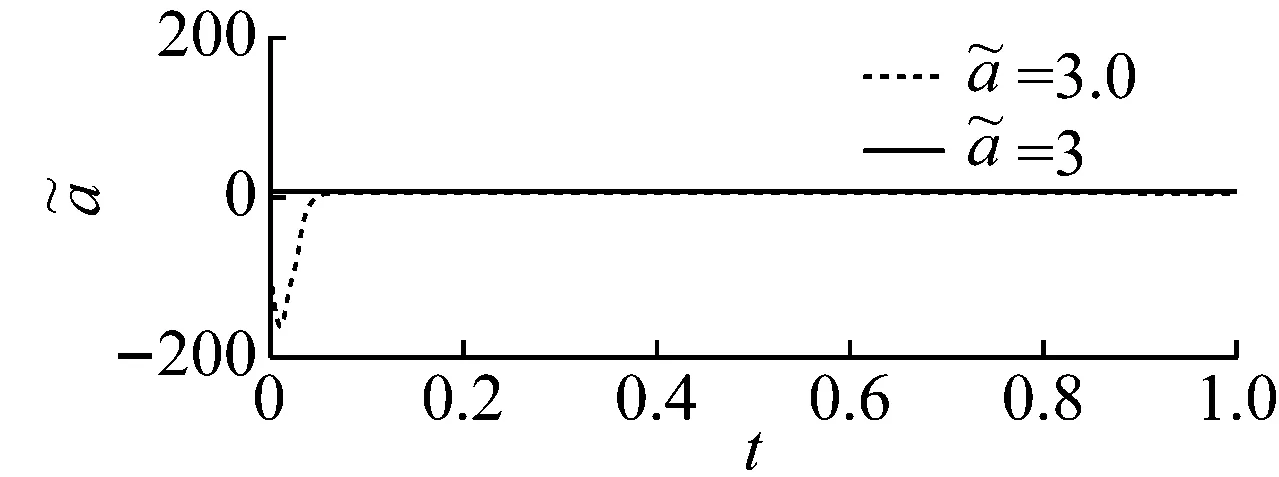
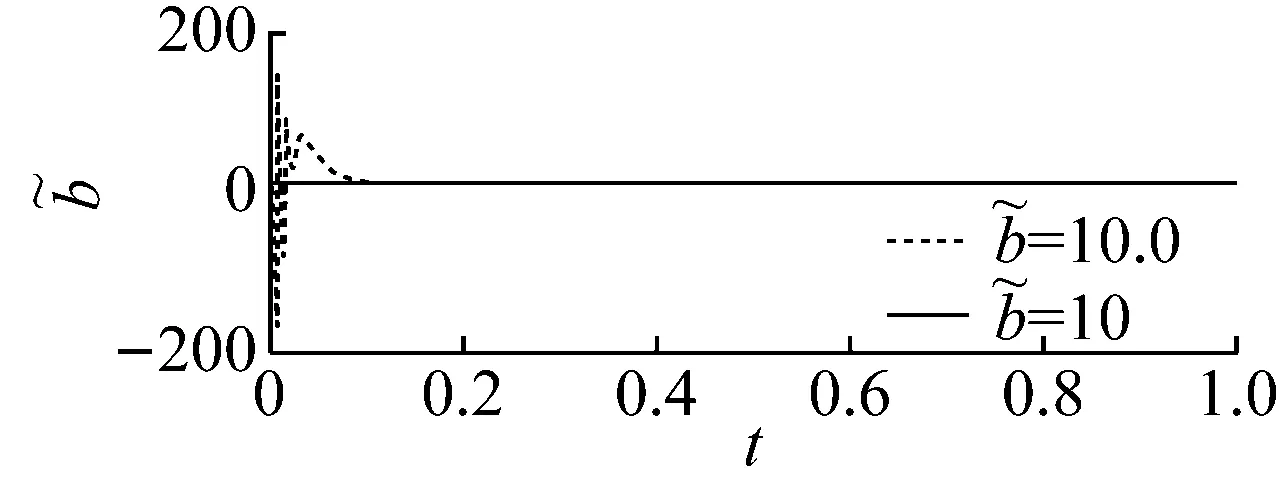
图12 参数和的收敛曲线

5 结 论

本文提出了一个超大范围的混沌系统，分析了系统的动力学特性，设计了系统的模拟电路。最后设计了一个自适应控制器和一个自适应滑模控制器，分别用于具有未知参数的混沌系统的全局稳定和给定信号的追踪与未知参数的辨识，数值仿真结果表明所设计控制器是有效的。

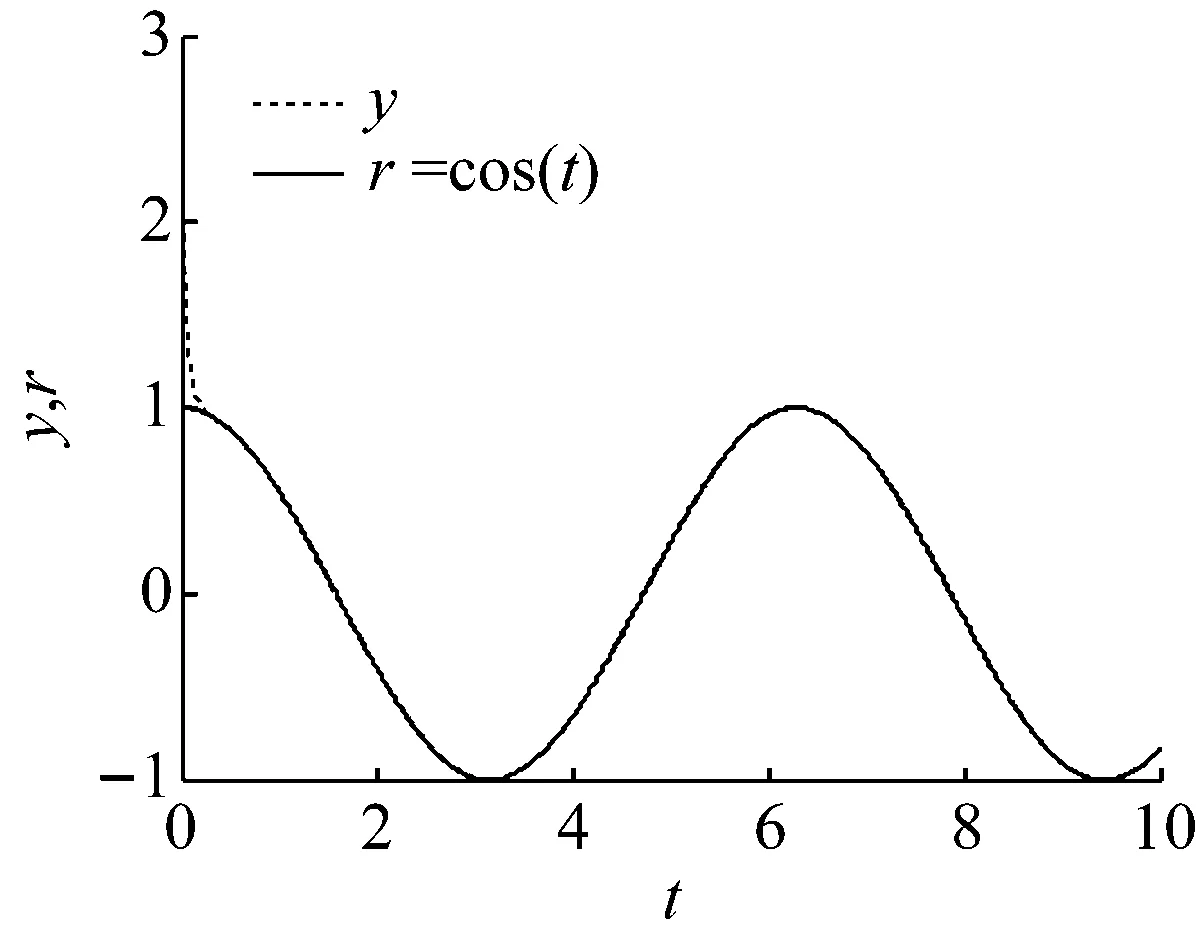
图13 跟踪cos(t)的曲线

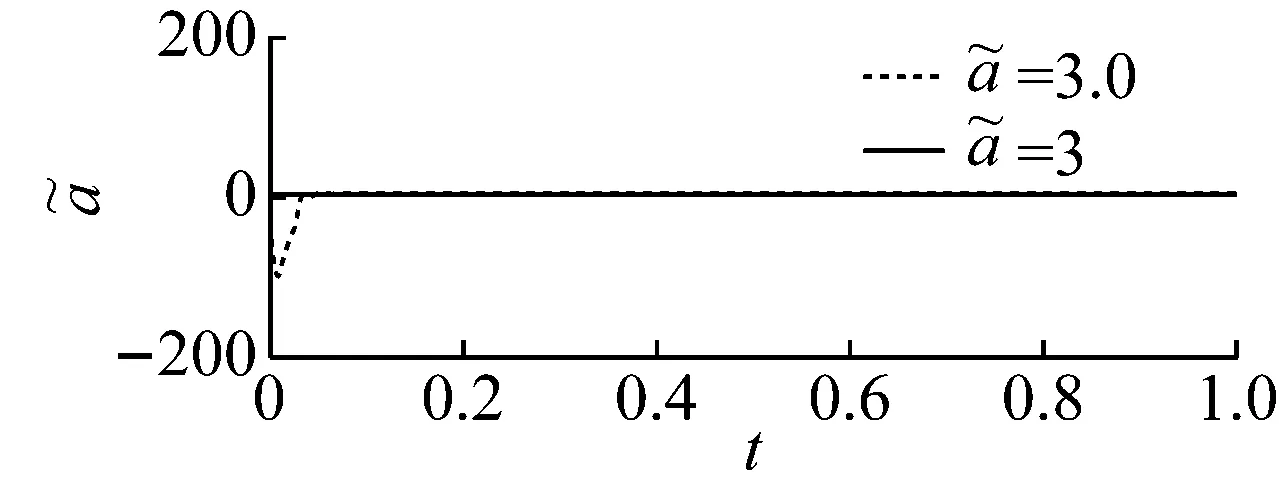
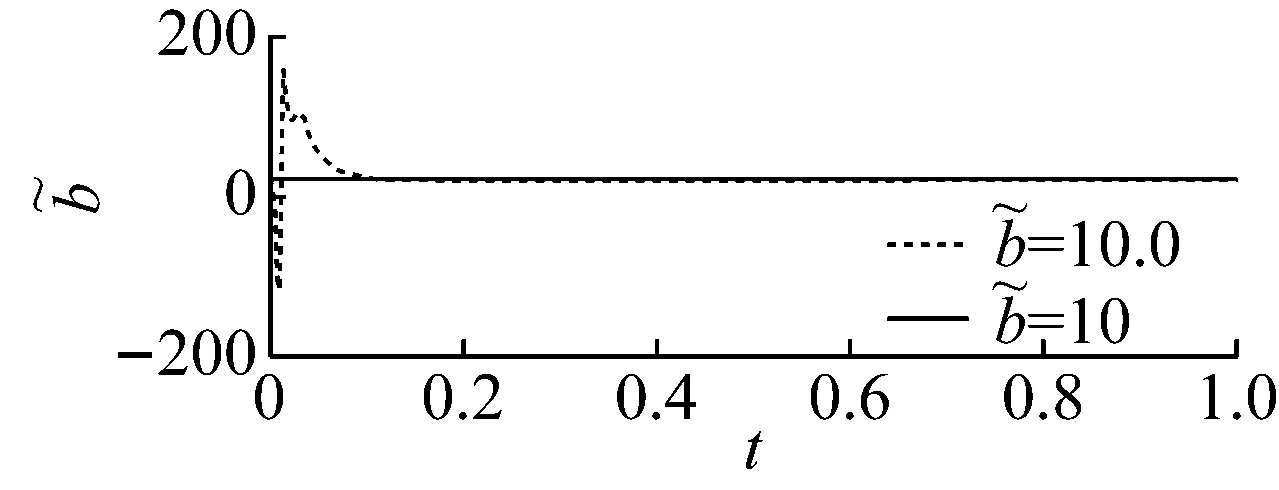
图14 参数和的收敛曲线