表层下缺陷对球-环系统的振动影响分析

张生光， 王文中

(1.中国航空发动机研究院,北京 101304；2.北京理工大学 机械与车辆学院,北京 100081)

高性能滚动轴承要求其在高速/重载等苛刻条件下长期保持高精度和工作状态稳定性，这不仅取决于轴承组件的几何精度，还取决于基体材料的组织性能及其稳定性。目前国内轴承加工的几何精度能够满足设计要求，但是长时间使用之后会导致精度缺失，原因是多方面的，其中由于轴承钢组织的不均匀性、非金属夹杂物或空穴等表层下缺陷的影响不可忽略，因此研究滚道表层下缺陷对轴承的影响十分重要。

目前很多研究者针对滚动轴承表层下缺陷进行研究，多集中在材料内部夹杂物对滚动轴承寿命或者接触压力、应力等分析上，研究了不同类型的非金属夹杂物的影响。如Ai[1]通过大量实验总结出轴承钢中夹杂物尺寸、数量以及位置分布等信息，并在此基础上研究其对滚动轴承寿命的影响。还有部分学者建立半解析模型，研究材料夹杂物对接触、润滑行为的影响，如Leroux等[2]和Zhou等[3]首先建立考虑夹杂物影响的三维接触模型，通过网格划分可模拟任意形状、尺寸及分布的夹杂物，研究了其对接触压力、表层下接触应力等的影响，并充分考虑了夹杂物质间的相互作用。张生光等[4]也在上述基础上通过半解析法研究了表层下空穴缺陷以及表面夹杂物对接触行为的影响，发现空穴以及硬质夹杂物对接触行为影响较大。

还有研究者通过理论与实验的方法研究表面缺陷对轴承振动特性的影响，目前轴承表面缺陷研究基本分为两种：一种是分布式缺陷，比如表面粗糙度、波纹度、滚动体尺寸不均等，这种缺陷通常与加工方法有关；另一种缺陷是局部式缺陷，例如裂纹、点蚀坑、滚道剥落等，这种缺陷通常是滚动轴承长时间服役后，由于疲劳而产生的。众多学者对此进行了研究。对于分布式缺陷，Yhland[5]早在1967年研究深沟球轴承波纹度测量时就指出了内外圈波纹度与振动之间的关系。随后，Mayer等[6]通过解析的方法来预测滚道偏心、滚动体尺寸不均以及轴承外圈表面波纹度等产生振动的频谱特性。Wardle[7-8]的研究从理论和实验的角度揭示了推力轴承内滚道、外滚道以及钢球波纹度对振动的影响，并且有效的验证了Yhland研究的结果。Choudhury等[9]利用理论模型预测了滚动轴承中分布式缺陷产生的振动，并且指出外圈缺陷引起的振动出现在公转频率ωc及其倍频处，而内圈缺陷引起的振动与BPFI以及轴的转动频率有关，并且振动大小与外圈缺陷引起的振动大小相当。Aktürk[10]，Harsha等[11]，Kankar等[12]也研究了滚动轴承波纹度对振动的影响，指出轴承在不同波纹度阶数时所处的运动状态以及主要振动、谐波振动所出现的频率位置，对前人的工作进行了有效的验证和补充。通过之前众多学者对滚动轴承波纹度的研究，可以看出波纹度阶数对轴承振动影响显著，通常振动出现频率与转轴频率fi、钢球公转频率fc、外圈缺陷频率BPFO和内圈缺陷频率BPFI相关。对于局部式缺陷，很多学者对此也进行了详细的研究，McFadden等[13-14]采用一串脉冲序列来模拟缺陷与轴承的碰撞激励，建立力学模型研究了单个或多个缺陷产生的振动，后来其结果由美国国家航空和宇宙航行局(National Aeronautics and Space Administration,NASA)研究人员通过非线性信号分析技术进行了实验验证[15]。Tandon等[16]也建立一个解析模型，同样采用脉冲序列模拟局部缺陷，并且考虑了脉冲持续时间、以及不同形状的脉冲序列(矩形脉冲、三角脉冲、半正弦冲击脉冲)对振动的影响，通过与实验的比较，精准地预测了轴向、径向载荷下，考虑滚动体、内外滚道局部缺陷的振动频率。Sopanen等[17-18]发展了包含局部和分布式缺陷的深沟球轴承动力学模型，其局部缺陷形状与单位阶跃函数相似，通过一个分段函数来表示，结果表明局部缺陷会在轴承缺陷频率(BPFO和BPFI)处产生较大振动。此外，Arslan等[19]，Rafsanjani等[20]，Kankar等[21]和Patel等[22]学者在滚道局部缺陷引起轴承振动方面也开展了大量研究，取得丰硕成果。但是这些研究多集中于表面缺陷的影响，只有Wang等[23]通过理论建模的方法研究了滚道内部夹杂物对轴承系统振动的影响。徐可君等[24]考虑了航空发动机中介轴承的滚动体缺陷，在滚动轴承动力学模型的基础上，通过数值仿真对比研究不同支承形式及内、外圈不同旋转方向对中介轴承振动特性的影响。剡昌锋等[25]还考虑了弹流润滑与表面局部缺陷的综合影响，建立了深沟球轴承局部缺陷的动力学模型，并通过轴承振动实验台对动力学模型进行了验证。

之前众多学者对非均质材料接触行为以及滚动轴承振动行为进行了富有成效的研究，但是尚缺少从实验角度研究表层下缺陷对轴承系统振动的影响。本文通过自主研发的球-环接触实验台模拟轴承点接触情况，并使用电涡流位移传感器直接测量钢球托架振动情况，研究表面缺陷和内部缺陷对球-环系统振动的影响。

1 球-环接触实验振动研究

由于滚动轴承中表层下缺陷难以精确定位与模拟，因此本研究采用球-环接触模型模拟滚动轴承点接触情况，揭示表层下缺陷对系统振动的影响。实验采用直径为25.4 mm的钢球与内径为100 mm铝合金圆环接触，实验分为以下三个步骤：①测量健康无缺陷的铝合金圆环与钢球接触时的振动情况；②在铝合金圆环上加工直径为1.5 mm通孔，测量通孔对球-环接触振动的影响，如图1(a)所示；③由铝合金圆环外侧向内侧加工直径为1.5 mm非通孔，其中该孔距圆环内表面非常近，但并未完全贯穿，从而模拟表层下缺陷对振动的影响，如图1(b)所示。

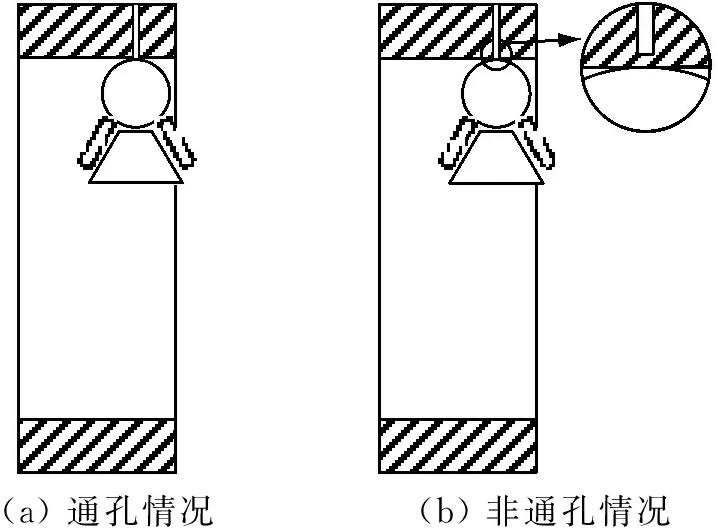
(a) 通孔情况(b) 非通孔情况

图1 通孔与非通孔位置示意图

Fig.1 Sketch maps of through-hole and non-through-hole position

1.1 实验装置

球-环振动测量实验装置如图2所示，其中图2(a)为实验系统示意图，工作原理如下所述：

伺服电机1通过联轴器2带动轴4转动，轴4通过两对背靠背角接触球轴承3支撑，轴4的另一端与圆环夹具5固结从而带动夹具5和圆环6旋转。另一方向，钢球7通过钢球托架8上的三个轴承支撑，从而可实现钢球7的定轴转动，载荷通过弹簧9拉动钢球托架8施加，加载后，铝合金圆环6可带动钢球7转动。电涡流传感器11置于钢球托架8正下方，测量其与钢球托架8之间的间隙变化即钢球7上下振动的位移，然后将数据传送至计算机10进行分析。实验台实物图如图2(b)所示。

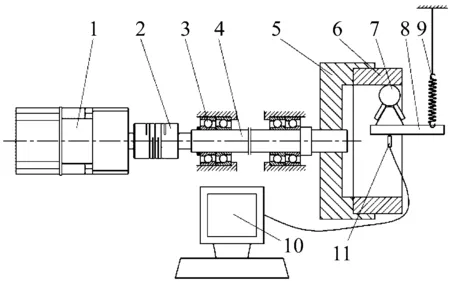
1.电机 2.联轴器 3.显示 4.轴 5.圆环夹具 6.圆环 7.钢球 8.钢球托架 9.弹簧 10.计算机 11.电涡流传感器

(a) 结构示意图

(b) 实物图

实验中位移传感器选用德国米铱公司eddyNCDT3100电涡流传感器，采样频率为14.4 kHz。电机选取三菱HC-KFS43电机，功率为400 W，伺服放大器为MR-J2S-40A。

1.2 无缺陷工况实验结果

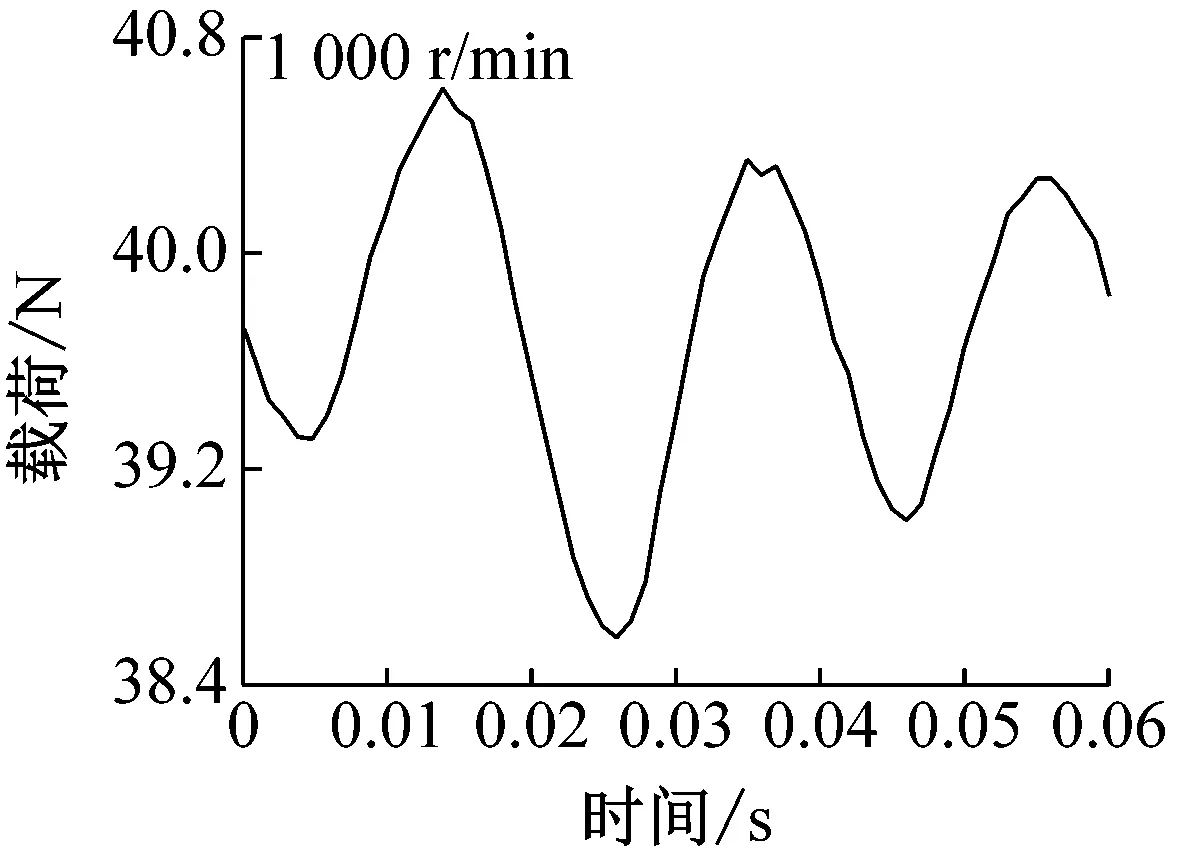
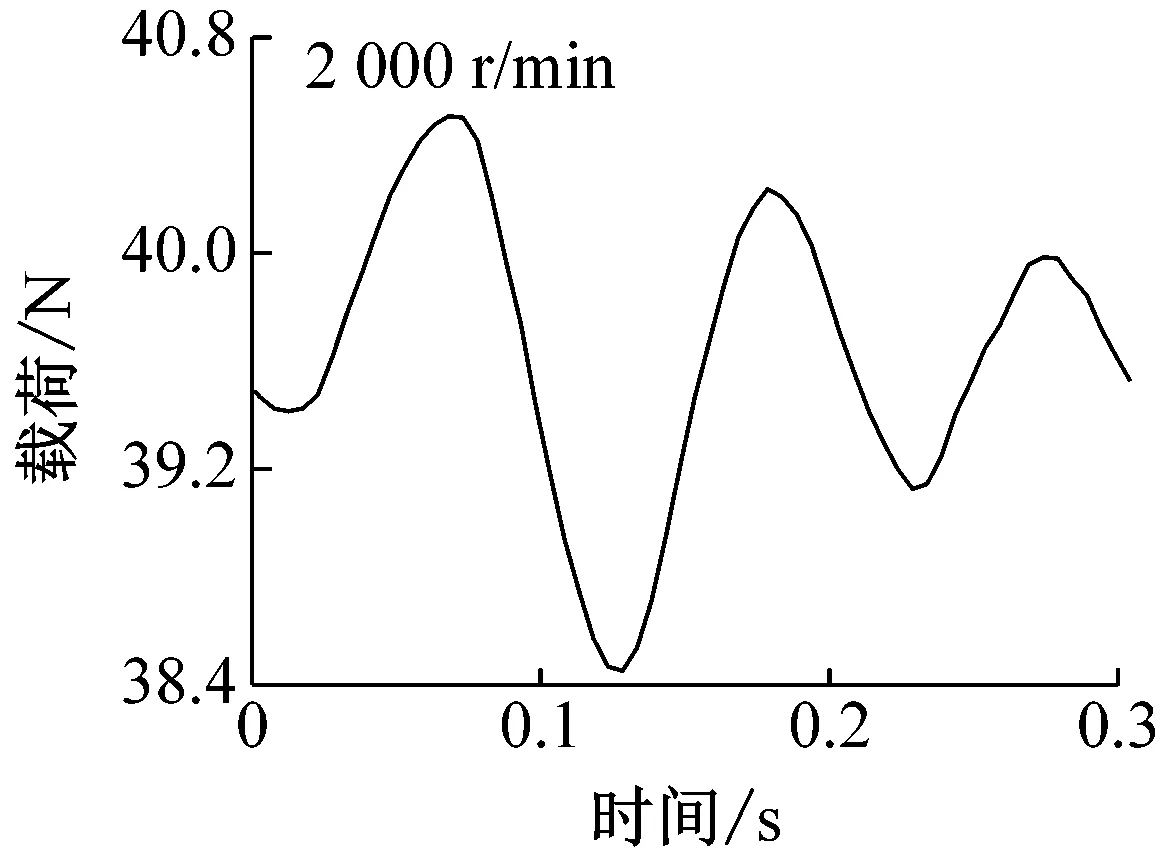
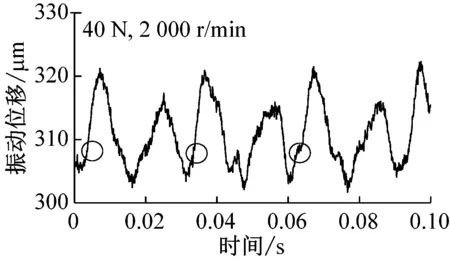
对于无缺陷的圆环，载荷为40 N时，钢球托架振动位移随时间变化结果如图3所示，此时最大赫兹接触压力为587 MPa。图中位移表示固定的电涡流传感器与钢球托架之间的间隙。由图可见，由于加工以及安装误差，圆环旋转时具有较大偏心(约为20 μm)，并且随着圆环的转动，钢球托架的振动并非严格的正余弦曲线，表明偏心情况比较复杂。转速较低时，电机振动较大，因此可见位移曲线毛刺较多，随着转速的增加，电机逐渐稳定曲线毛刺也逐渐减小。载荷变化情况如图4所示，不同转速对载荷影响相差不大；相似地，转速较高时载荷曲线较为平滑，并且载荷随时间变化规律与位移完全相反，这是由于位移较小时，位移传感器与球托之间间隙较小，二者距离较近，此时加载用的弹簧被拉伸较长，因此力传感器载荷较大，反之亦然。

1.3 圆环表面缺陷工况实验结果

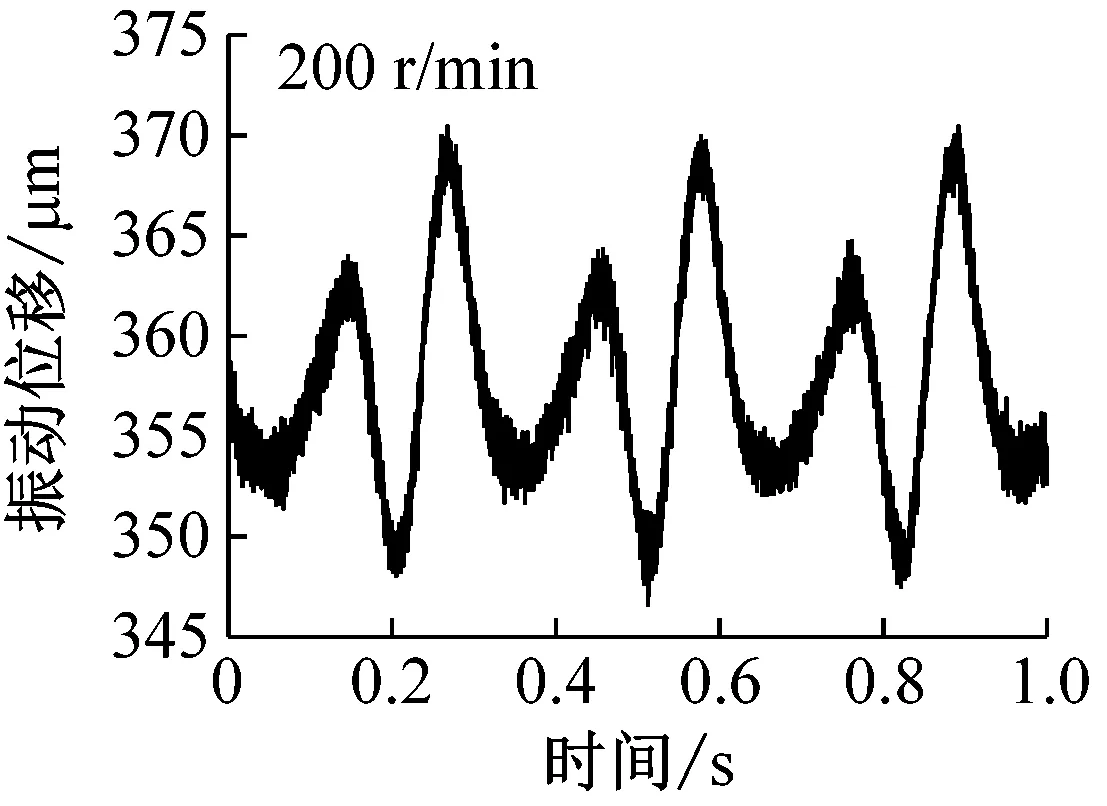
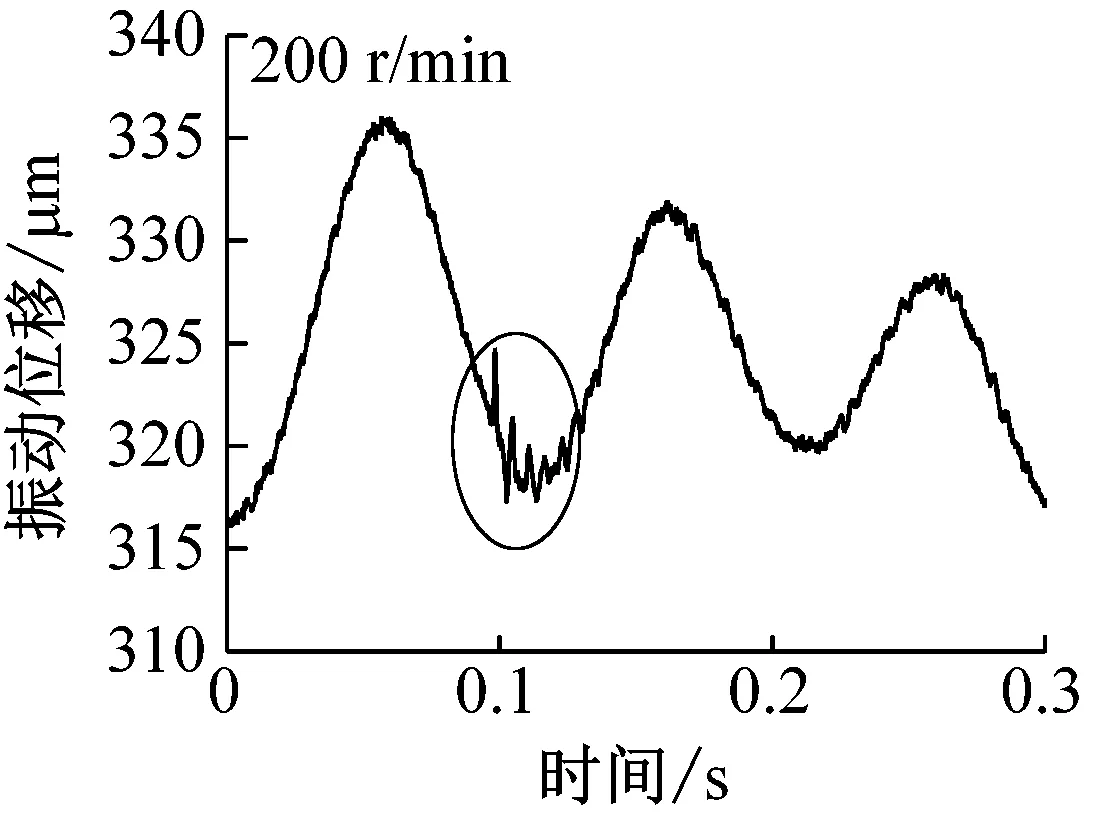
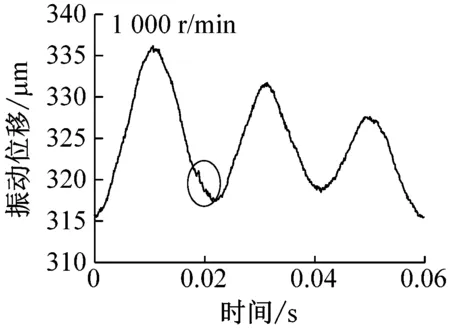
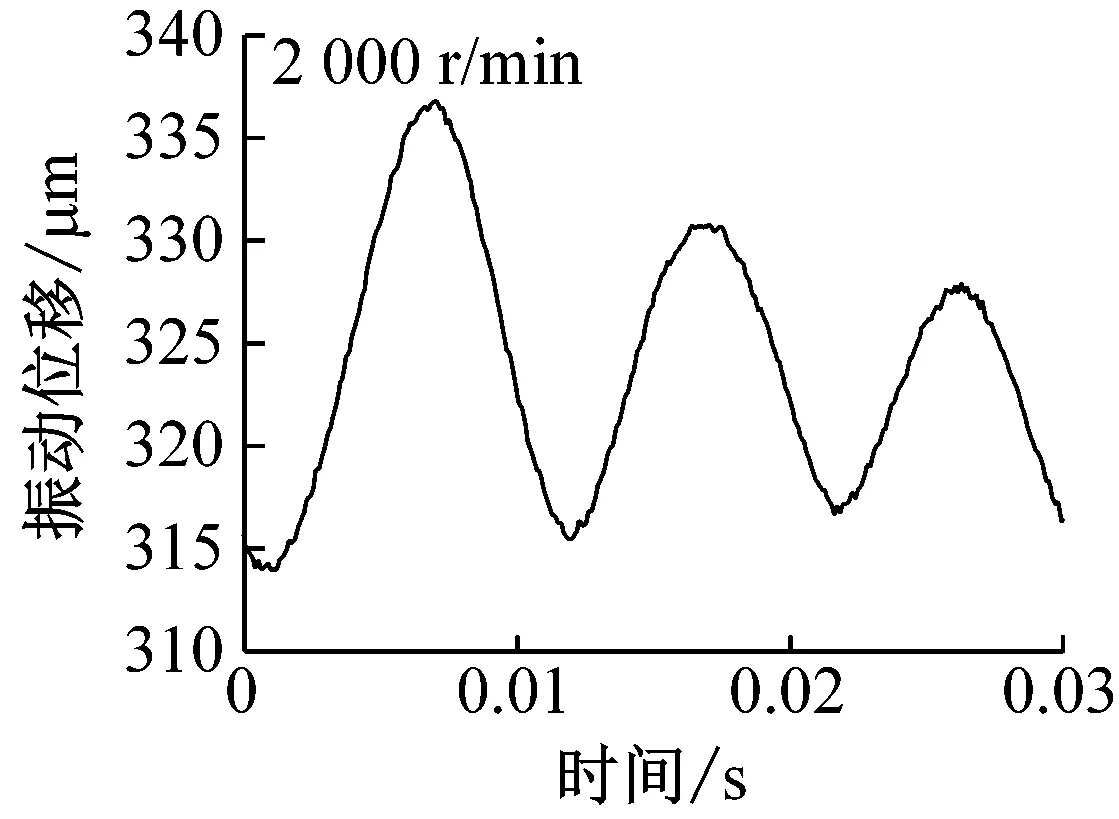
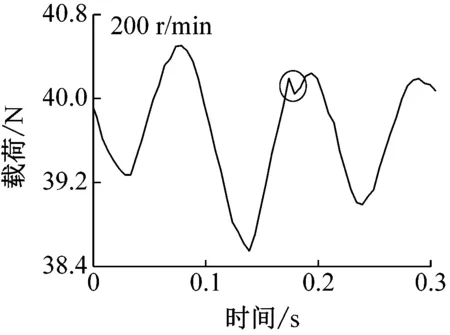
为研究表面缺陷对系统振动的影响，在铝合金圆环上加工1.5 mm通孔，使得圆环旋转时此通孔正好通过钢球，如图1(a)所示。图5和6给出了不同转速下的表面缺陷引起的振动位移和载荷变化。

(a) 转速200 r/min

(b) 转速1 000 r/min

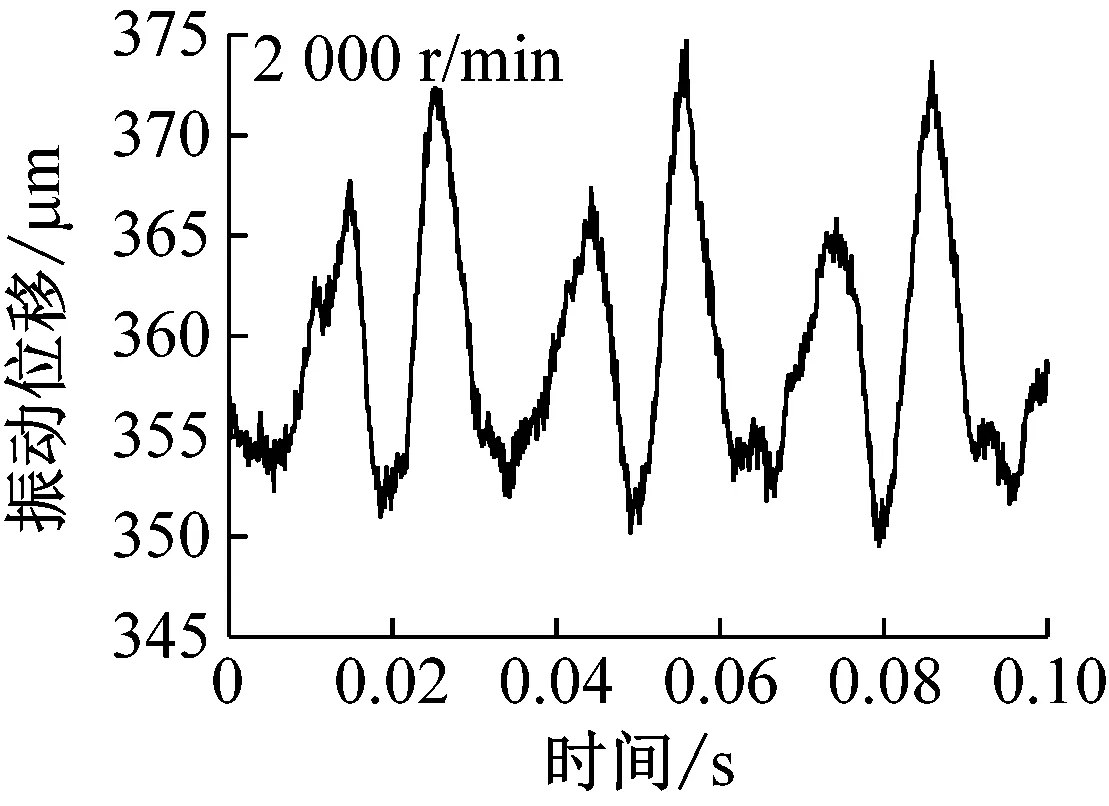
(c) 转速2 000 r/min

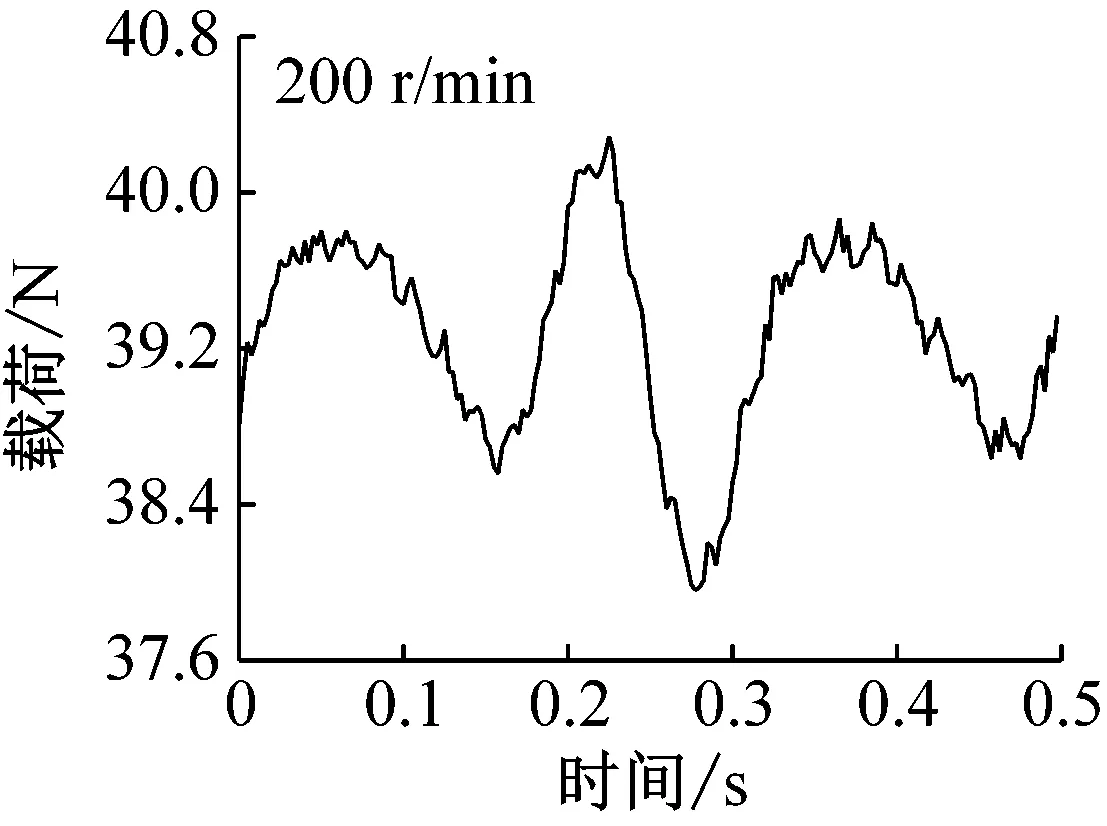
(a) 转速200 r/min

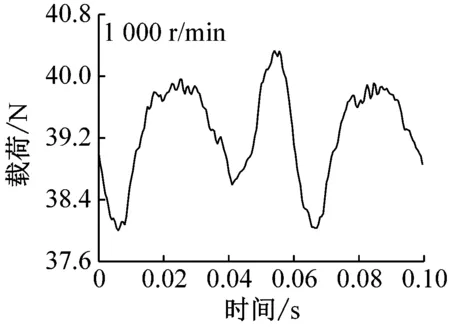
(b) 转速1 000 r/min

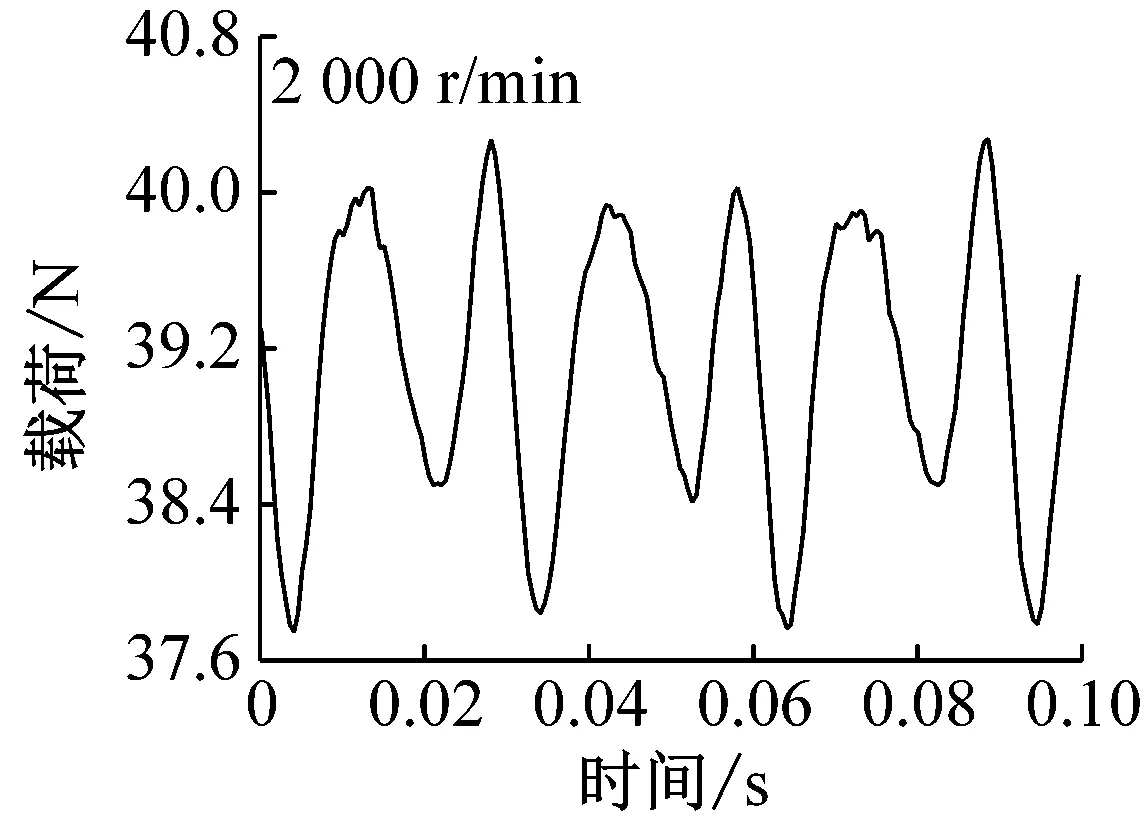
(c) 转速2 000 r/min

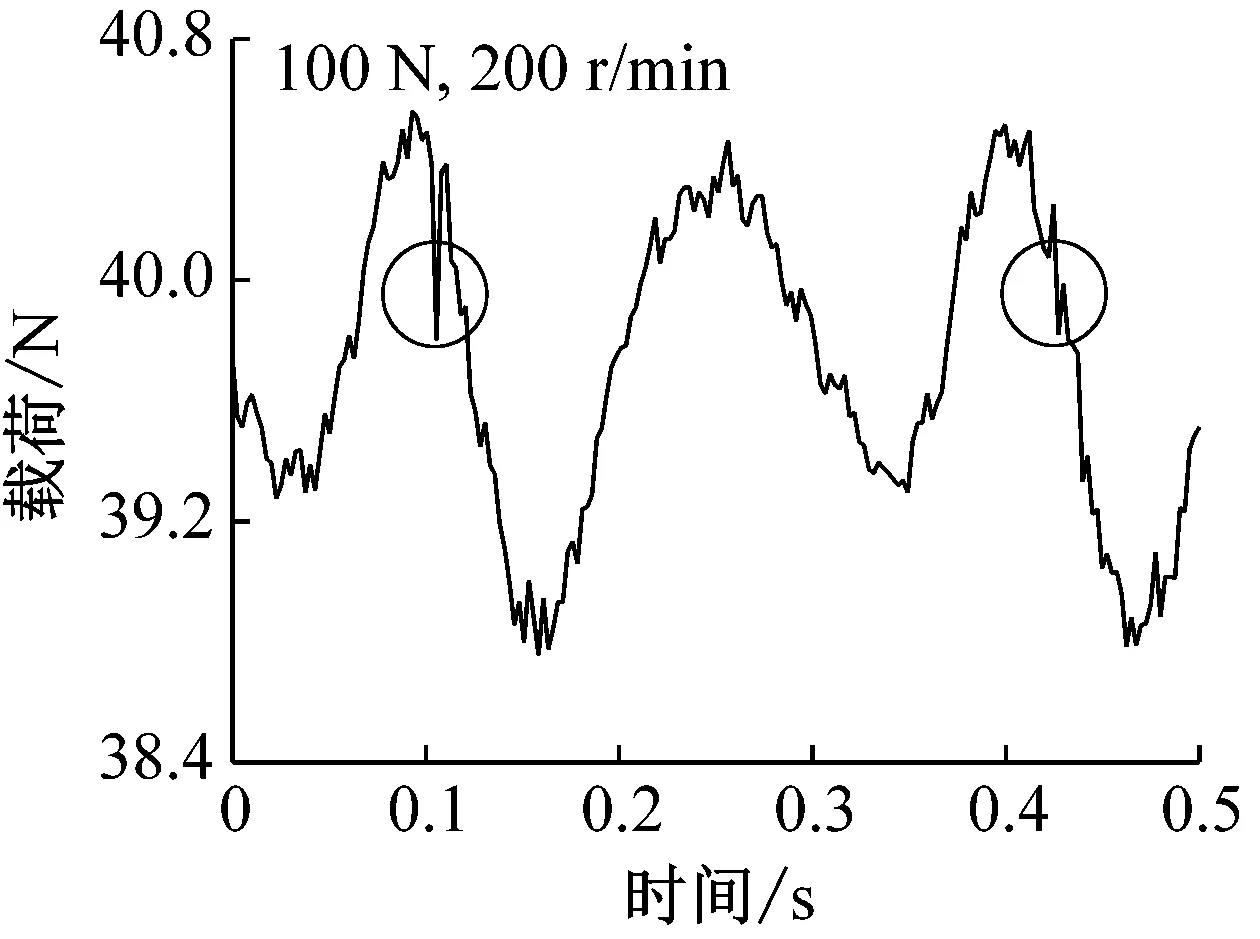
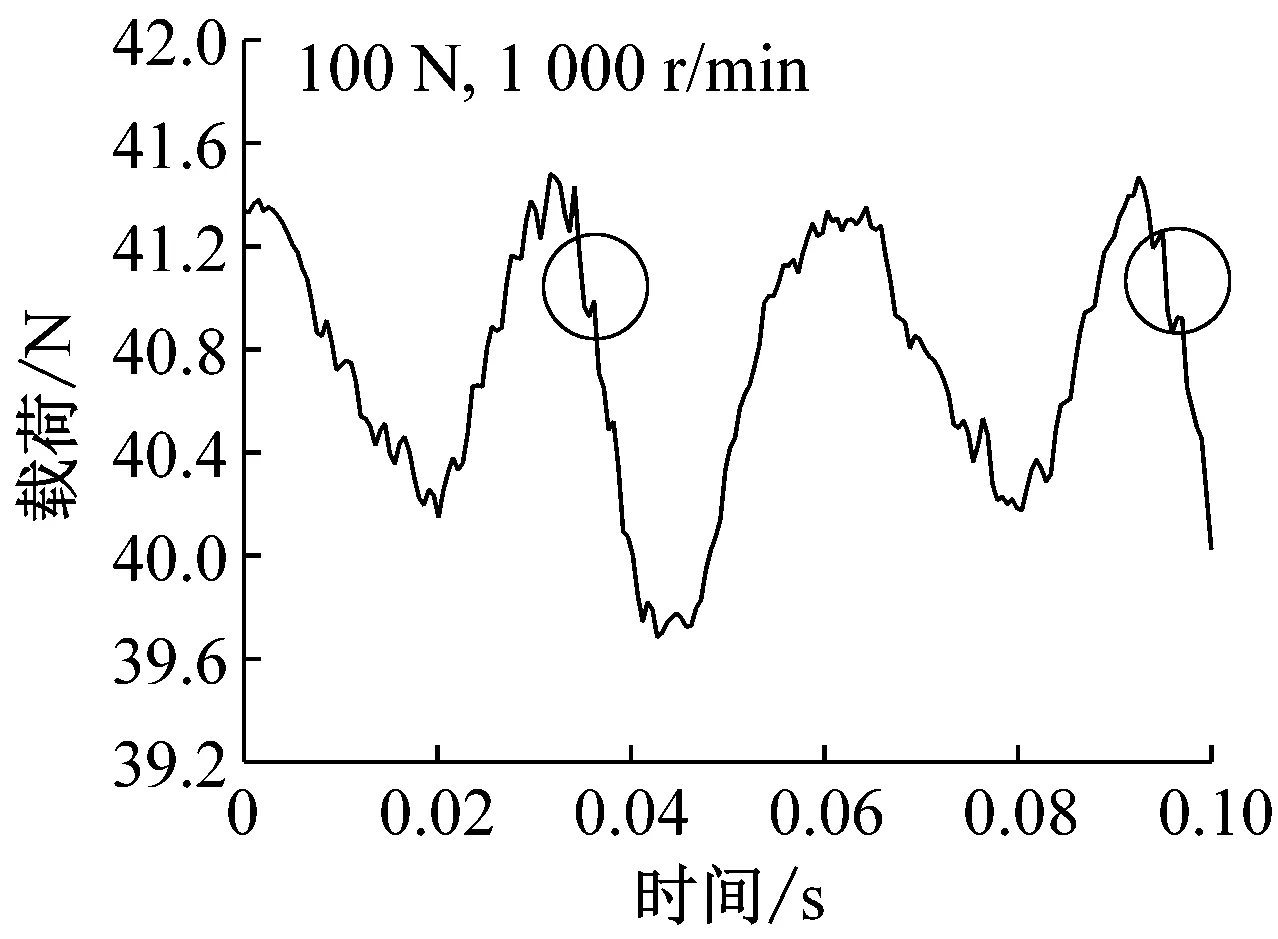
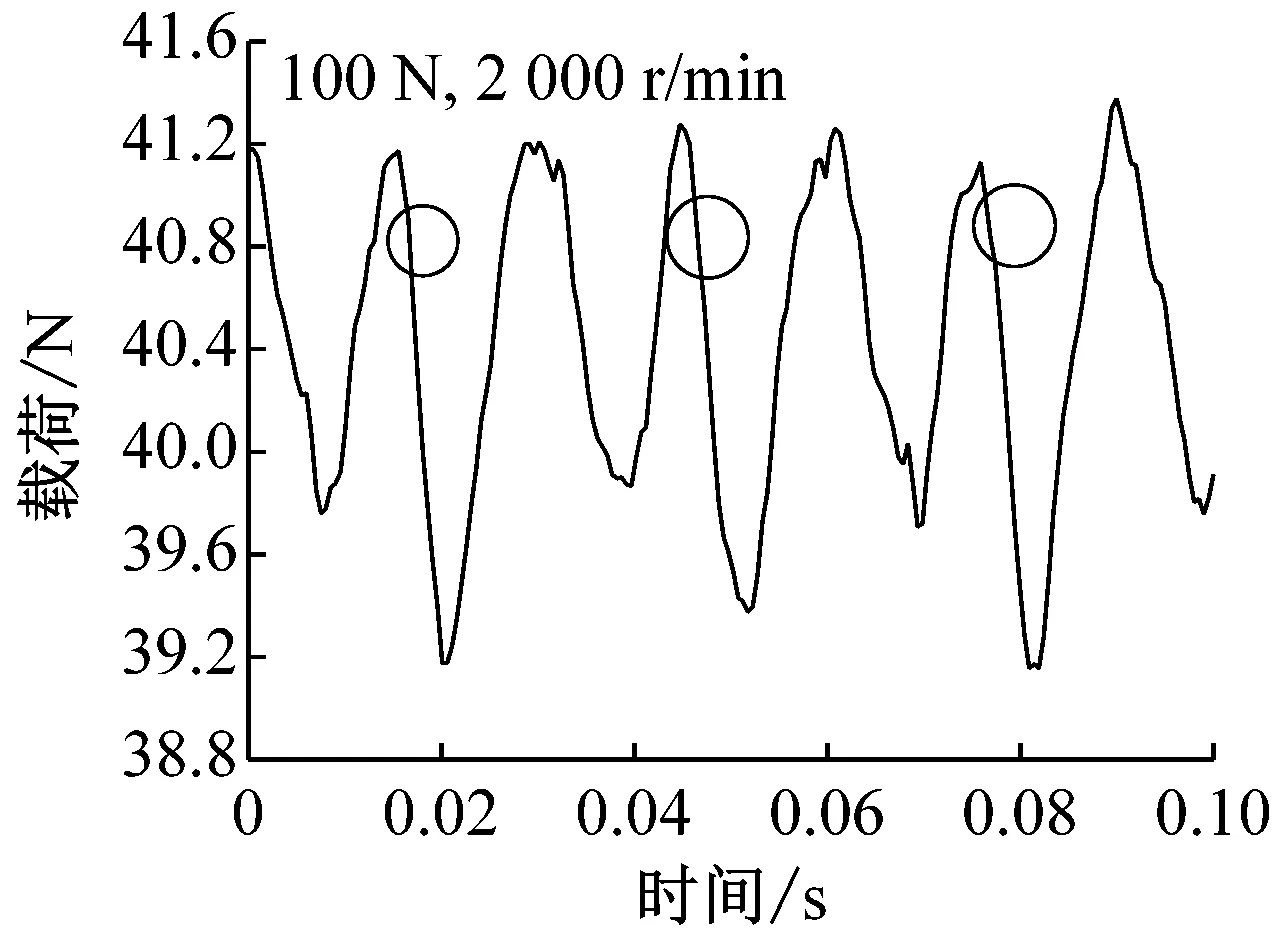
载荷40 N时，钢球托架振动位移随时间变化如图5所示。转速较小时(200 r/min)，通孔对振动的影响清晰可见，如图中圆圈部位标出。由于通孔的存在，钢球通过时具有掉进通孔内的趋势，因此钢球以及托架整体会向上移动，导致位移传感器与钢球托架距离增大，当钢球离开通孔后，由于之前掉入距离较大，随后会产生振动并逐渐衰减至平稳状态。随着转速的增加，由图可见，通孔对振动的影响变小(1 000 r/min)甚至消失(2 000 r/min)，即圆环高速旋转时，由于速度较大，通过通孔时直接跃过，最终导致高速工况下振动较小。需要指出电涡流位移传感器采样频率为14.4 kHz，当转速为2 000 r/min时，每转采样次数高达432次，对于直径为1.5 mm的通孔，不会由于采样频率不足而产生数据丢失。载荷变化情况如图6所示，由图可见，低速时，由于通孔的存在确实会对载荷产生影响，并且载荷随时间变化规律仍与位移相反，本实验所用力传感器采样频率(最高1 kHz)未能达到位移传感器精度，因此钢球离开通孔后载荷振动衰减情况没有出现，高速时，同样未能发现通孔对载荷的影响。

(a) 转速200 r/min

(b) 转速1 000 r/min

(c) 转速2 000 r/min

(a) 转速200 r/min

(b) 转速1 000 r/min

(c) 转速2 000 r/min

1.4 圆环内部缺陷工况实验结果

上述研究表明表面缺陷对球-环系统位移以及载荷均有较大影响。工程实际中缺陷也可能出现在材料内部，本节研究圆环内部缺陷对系统振动的影响，采用非通孔模拟内部缺陷，即采用工艺加工距圆环内表面很近的径向盲孔，且圆环内表面未受到损伤，但由于工艺限制，未能得到孔底部与圆环内表面的实际距离，如图1(b)所示。

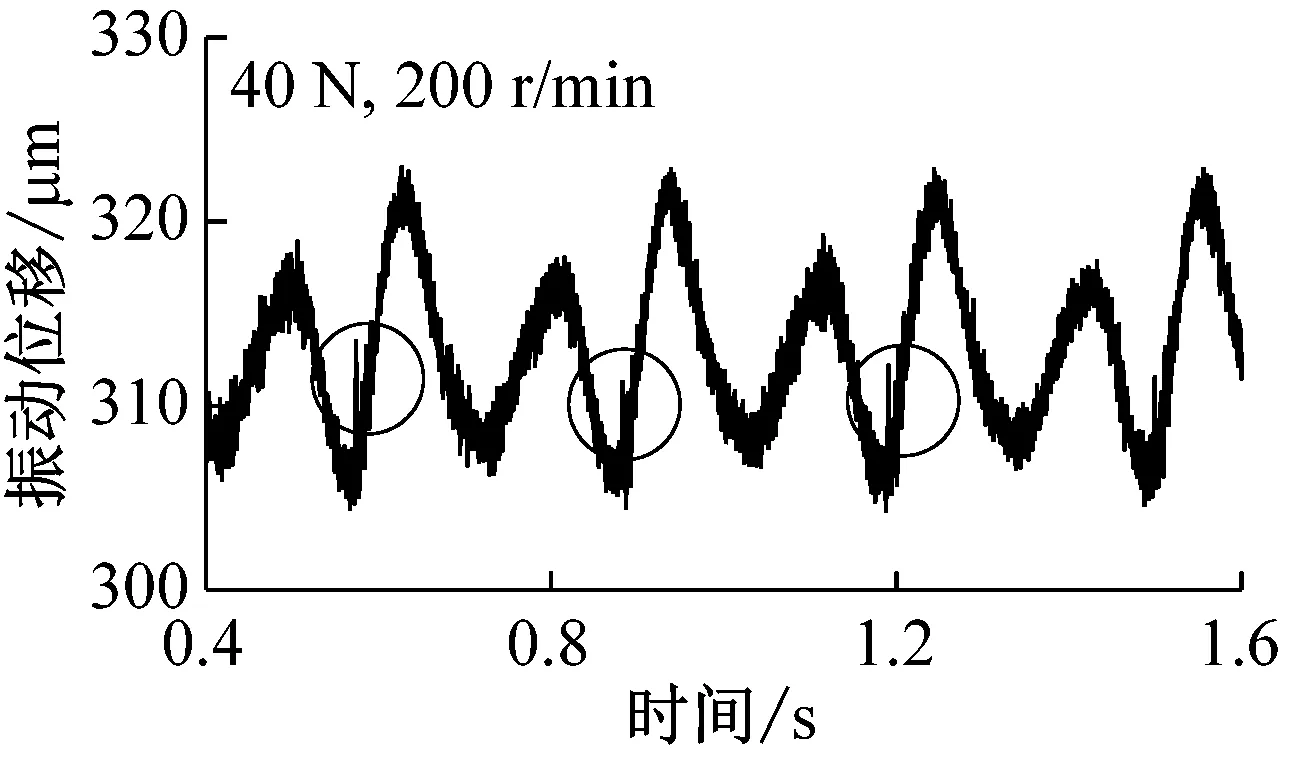
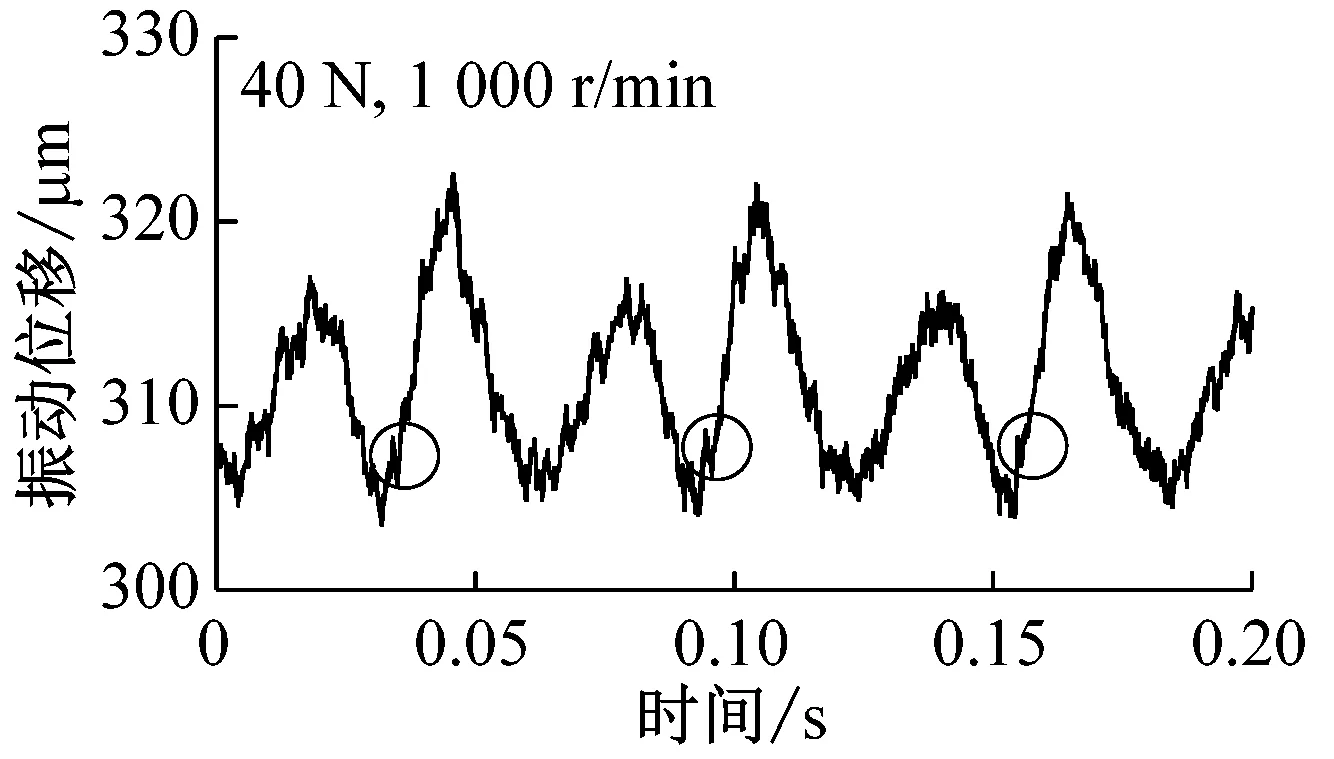
不同转速时，非通孔对位移影响如图7所示(载荷40 N)。由图可见，低转速时，内部缺陷对系统振动的影响较大，随着转速的升高，缺陷影响越来越小，与图5所示结果相似。当转速达到2 000 r/min时，圆环内部缺陷的影响几乎消失。对应的载荷测量结果如图8所示，同样低速时(如200 r/min)内部缺陷对载荷影响较大，随着转速的升高，影响逐渐减小，直至消失。

转速为100 r/min时，非通孔对球托振动影响如图9所示，低速时由于电机振动导致测量曲线具有较多毛刺。图9(a)中，载荷8 N，圆圈位置为缺陷位置，内部缺陷影响几乎不可见。随着载荷的增加，如图9(b)所示，载荷为16 N，圆圈标识位置为内部缺陷位置，虽然曲线毛刺较大，但是缺陷位置处振动明显，由此可见，表层下缺陷确实引起系统额外振动。随着载荷的进一步增加，如图9(c)和(d)所示，缺陷引起的振动更加明显，但相比于通孔影响还是较小。这一结果也与表层下空穴或杂质产生表面特征位移的计算结果一致：随着载荷的增加，杂质或空穴引起的表面特征位移逐渐增加。

(a)

(b)

(c)

(a) 转速200 r/min

(b) 转速1 000 r/min

(c) 转速2 000 r/min

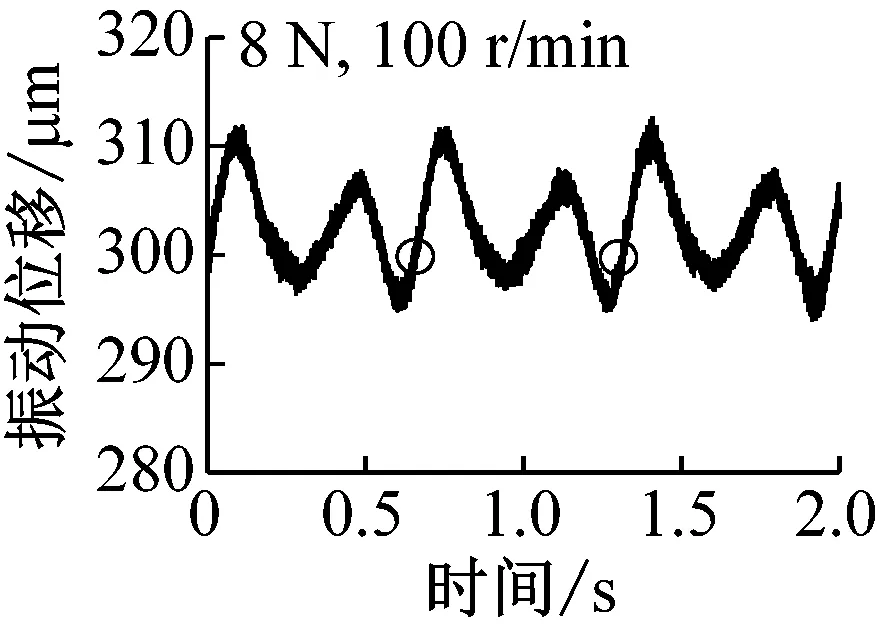
(a) 载荷8 N

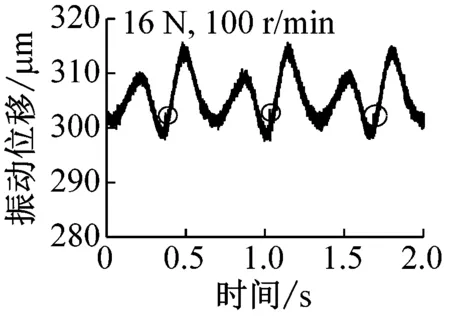
(b) 载荷16 N

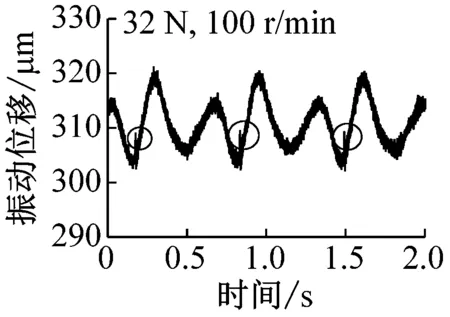
(c) 载荷32 N

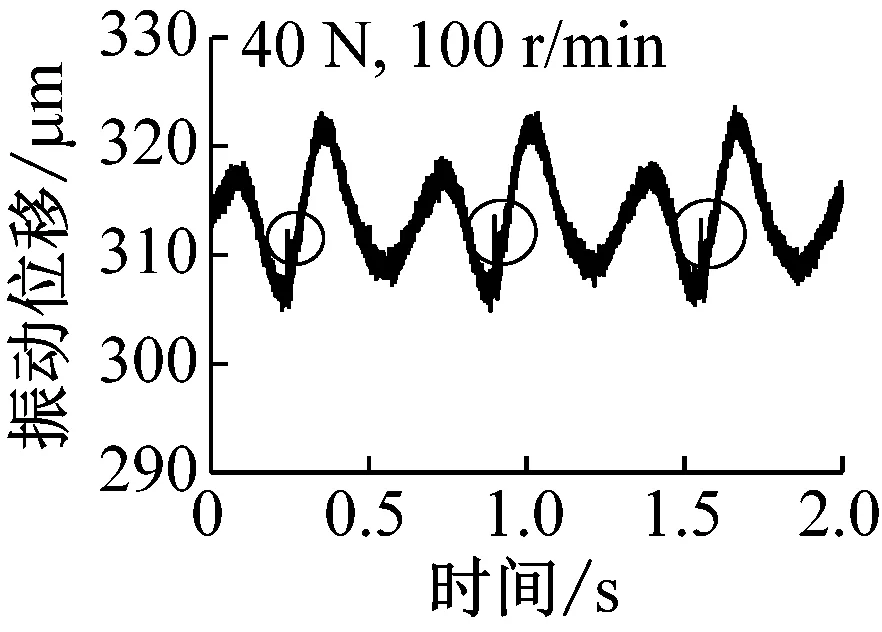
(d) 载荷40 N

综上球-环振动实验的研究，结果表明表面缺陷以及内部缺陷确实对系统位移以及载荷具有影响，并且表面缺陷影响较大。而且随着载荷的增加，内部空穴的影响逐渐增大。但是随着转速的增加，空穴影响逐渐减小，为探究其原因，下面采用理论模型分析这一情况。

2 球-环接触动力学建模分析

2.1 理论建模

由于实验模型的复杂性，本节将其简化为旋转圆环与钢球接触，载荷加载在钢球上，根据图6和图8的实验结果，由于圆环同心度误差造成的接触载荷波动为3～4 N，因此加载时直接加载正弦波动载荷以模拟圆环不同心工况。

对钢球进行运动分析，其运动控制微分方程为：

(1)

式中:m为钢球质量；c为阻尼；y为钢球竖直方向坐标，钢球与圆环刚接触时y=0；f为圆环同心度误差引起的波动载荷，根据实验结果取f=1.5 N；Qy为弹性变形引起的接触力，可通过位移载荷系数与变形的乘积求得：

Qy=Kδ1.5

(2)

式中:K为位移载荷系数，计算方法见参考文献[23]，通过计算确定K=1.633×1010N/m1.5；δ为钢球与圆环接触时的弹性变形，考虑深度为h的缺陷通过钢球时，弹性变形为：

(3)

通过四阶Runge-Kutta法对运动微分方程(1)求解可得到钢球振动的位移y以及接触载荷Qy，从而可以与前述实验结果进行对比。

2.2 计算结果

由于钢球振动位移与载荷变化相关，因此这里仅从钢球位移角度进行分析，研究不同转速情况振动衰减的原因。

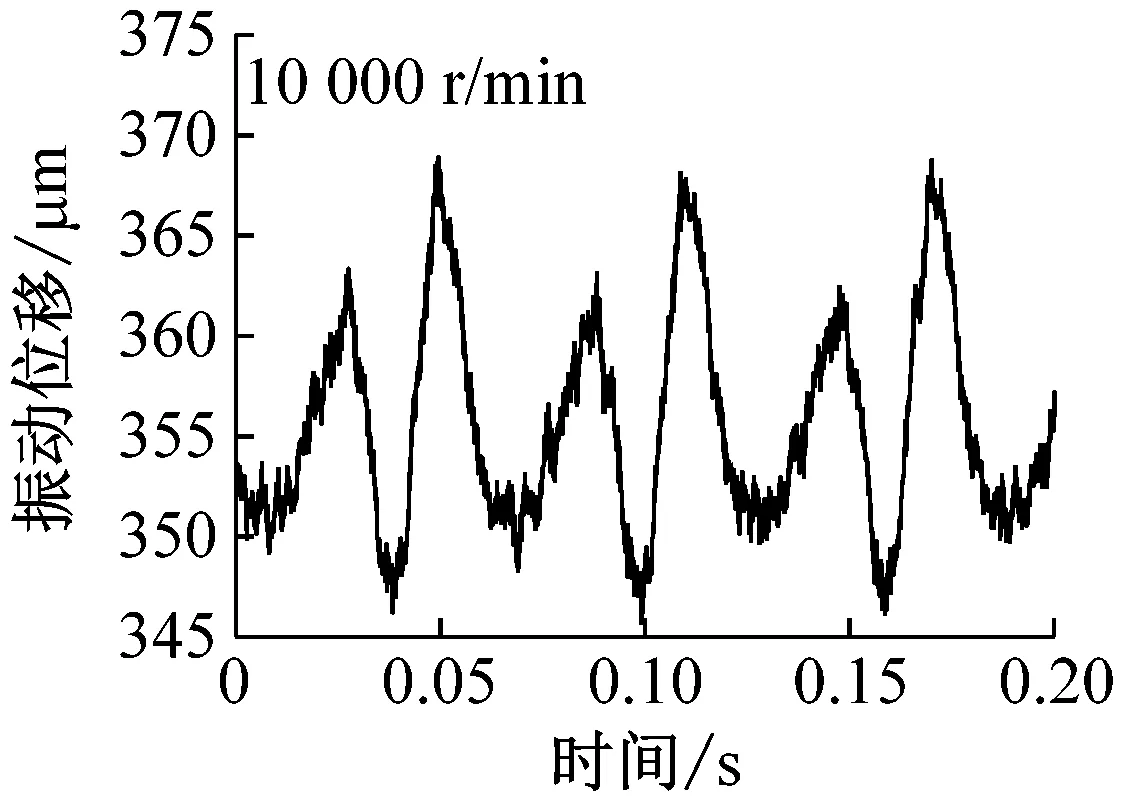
图10为不同阻尼工况下，缺陷对系统振动的影响结果，分为低速200 r/min和高速2 000 r/min两种工况。滚动轴承的阻尼可取为200 Ns/m[26]，对于球-环系统，200 Ns/m阻尼时计算结果如图10(a)所示。由图可见，低速与高速时缺陷均对系统振动影响较大，并且高速时，影响更为显著，这明显与前述实验结果相矛盾，经过分析发现，球-环实验台所用装置通过弹簧系统加载，与普通轴承系统不同，其阻尼远大于200 Ns/m，因此图10(b)和(c)还给出了更大阻尼对应的位移结果。由图可见，随着阻尼的增大，缺陷的影响逐渐减小，并且阻尼对高速工况的影响十分明显，当阻尼达到10 000 Ns/m时，高速工况下，表面缺陷的影响已经很小，而低速工况下，表面缺陷影响仍然比较明显，这与实验结果比较一致。因此，可以推断，对于前述实验结果，由于加载系统阻尼较大，高速时，缺陷引起的振动很快被阻尼吸收，因此实验结果中并未显示缺陷的影响。需要指出的是由于理论模型的简化，实验中的阻尼也并非一定为10 000 Ns/m左右，但是应远大于滚动轴承中的阻尼。

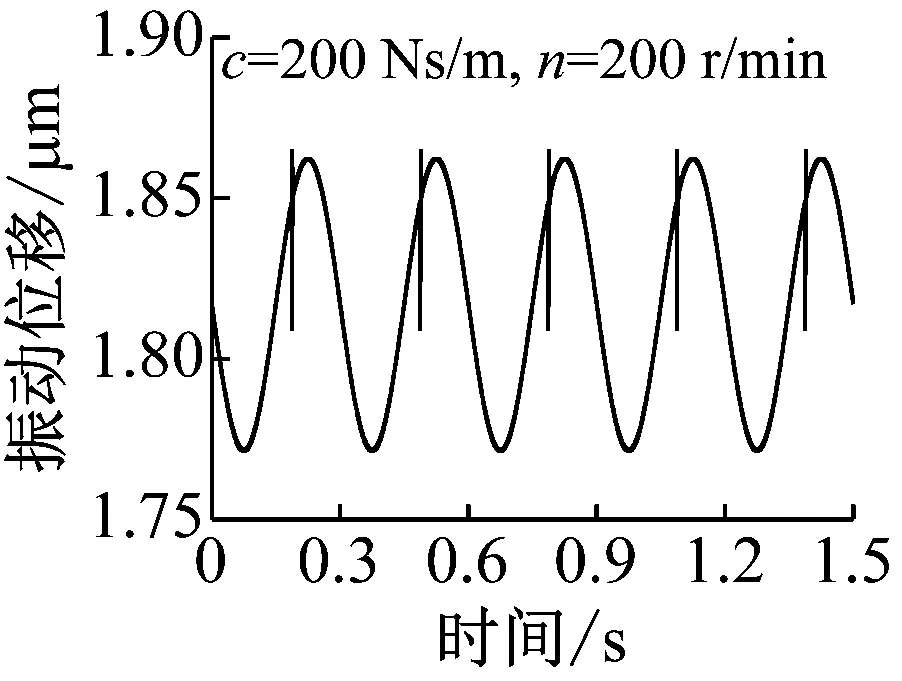
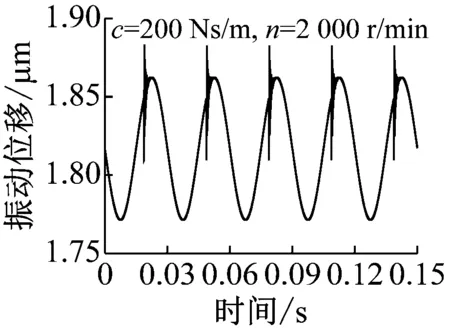
(a) 阻尼c=200 Ns/m

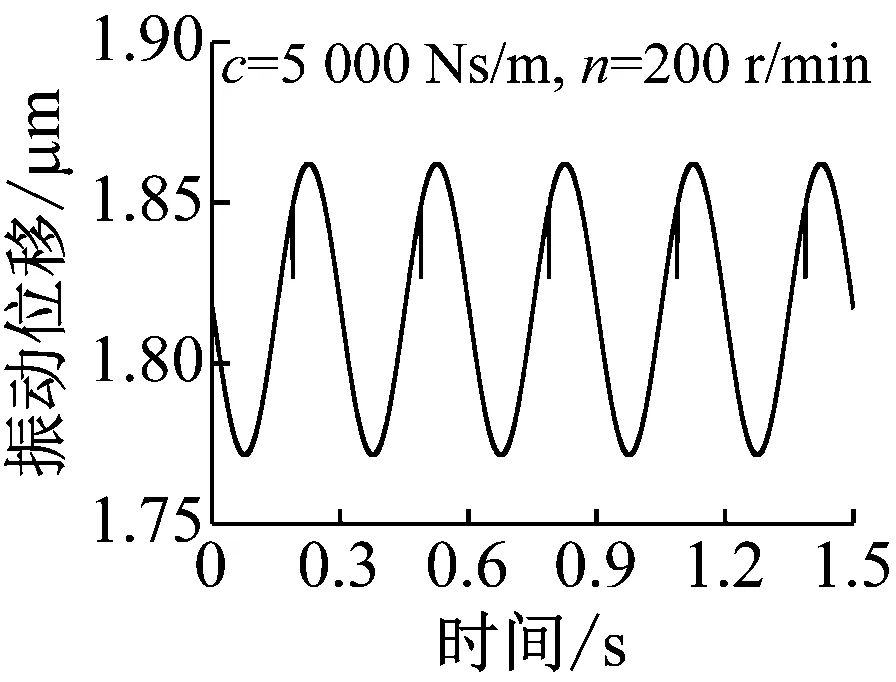
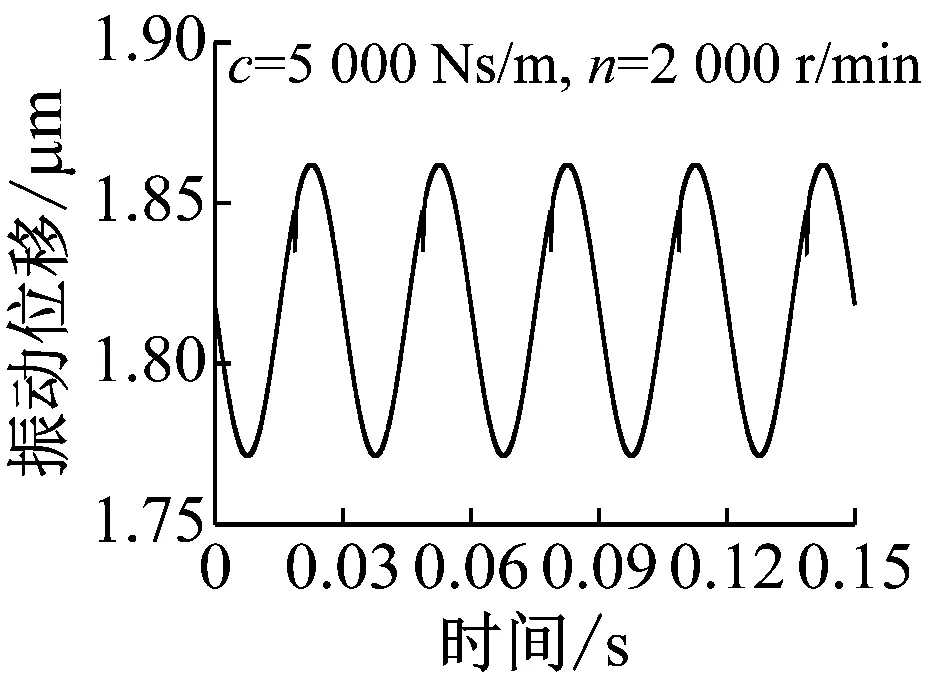
(b) 阻尼c=5 000 Ns/m

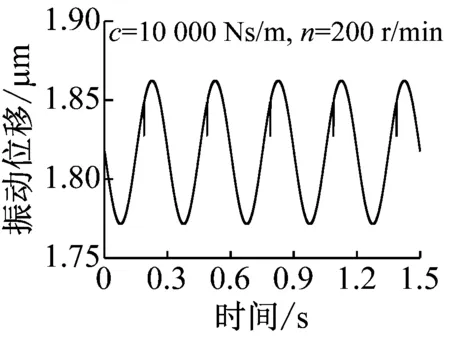
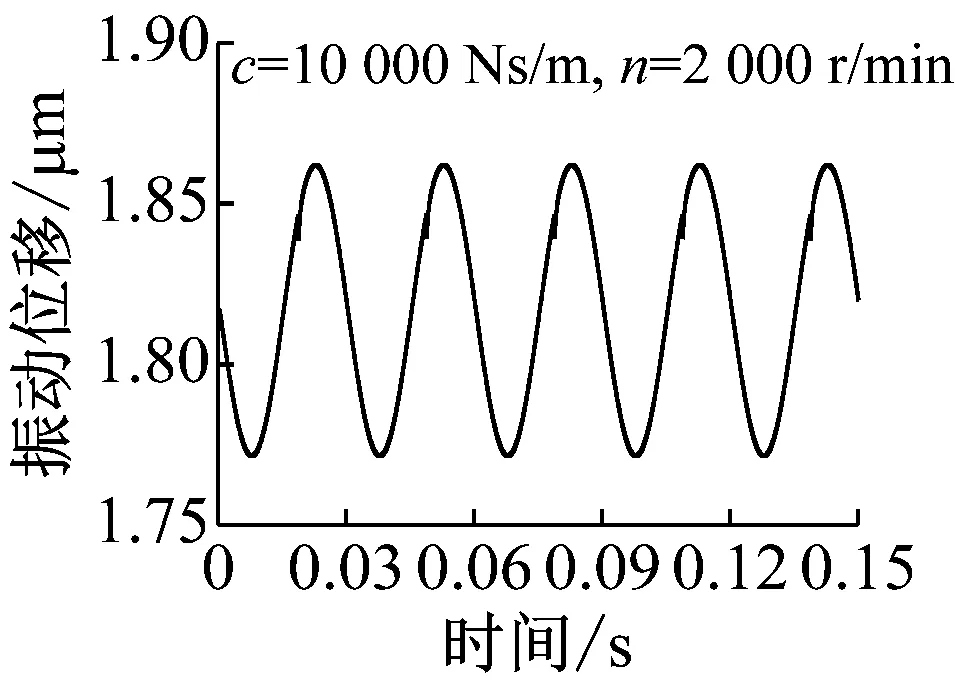
(c) 阻尼c=10 000 Ns/m

Fig.10 The effect of the defect on the vibration of ball-ring system at different damping

需要说明的是，轴承外环的厚度、非通孔的深度等参数与系统振动特性相关，本研究采用铝合金圆环进行实验和理论计算，由于加工工艺与测量技术限制，未能实验研究非通孔的深度对系统特性的影响，有待后续进一步研究；本研究中理论模拟主要为探究随着转速的增加，缺陷影响逐渐减小的原因，因此使用表面缺陷进行模拟，但是通过改变缺陷深度h还可以研究不同深度的非通孔对系统振动特性的影响。

3 结 论

通过球-环接触模型模拟滚动轴承滚动体与外滚道接触，研究表面或表层下缺陷对球-环系统振动特性的影响。实验结果表明:

(1) 表层下缺陷确实会影响系统振动行为。随着载荷增大影响逐渐增大，但是明显小于表面缺陷的影响。

(2) 缺陷的影响与系统阻尼密切相关，在高阻尼情况下，随着转速升高缺陷对系统振动影响逐渐减小。

本文结果表明由于服役过程产生或材料本身存在的缺陷不仅会影响接触性能，也会影响系统振动特性及精度保持性。