基于数学史的数学文化内涵课例分析

◎ 汪晓勤

一、引 言

《普通高中数学课程标准（2017年版）》（以下简称“《标准》”）将“四基”“四能”“核心素养”和“情感信念”列为数学课程的目标。其中，关于“情感信念”目标的表述是：“通过高中数学课程的学习，提高学习数学的兴趣，增强学好数学的自信心，养成良好的数学学习习惯；树立敢于质疑、善于思考、严谨求实的科学精神；认识数学的科学价值、应用价值、文化价值和审美价值；进一步促进学生全面、可持续发展。”［1］这里，学习兴趣、自信心、习惯、科学精神都属于数学学科德育的内涵，而数学的价值则与数学文化密切相关。

《标准》在“课程结构”中指出，“把数学文化融入课程内容中”。《标准》在“教学建议”中要求：“在整个数学教学中，教师应当有意识地结合相应的教学内容，引导学生了解数学的发展，认识数学在科学技术、社会发展中的作用，体会数学的科学价值、应用价值和文化价值，提升学生的科学精神、应用意识和文化素养。”［1］

由上述可见，提升数学文化修养，将数学文化融入数学教学，是数学课程对每一位数学教师的要求。普通高考考试大纲中对于数学文化内容的要求，又引发了中学教师对数学文化的特别关注。然而，高考题中的数学文化只充当了“标签”的角色；数学文化在中学的境遇依然是“高评价低应用”，数学文化融入数学教学的理想案例并不多见，数学文化应有的教育价值在实践中并没有得到充分体现。究其原因，是人们对数学文化的内涵还没有清晰的认识，所掌握的适合于教学的数学文化素材少之又少，对于数学文化素材的运用方式也不甚了了。

数学史是数学文化的重要组成部分。实践表明，在数学教学中，数学史可以揭示知识之谐，呈现方法之美，营造探究之乐，达成能力之助，展示文化之魅，实现德育之效［2］。但在HPM（History and Pedagogy of Mathematics）领域，迄今尚未有人对“文化之魅”的价值展开深入的分析和讨论。

本文试图根据西方学者关于数学史教育价值的讨论，结合课程标准，对课堂上基于数学史的数学文化元素进行分类，并通过HPM课例的分析，说明分类框架的适用性，为数学文化融入数学教学提供一定的参考。

二、基于数学史的数学文化内涵

根据西方学者所总结的数学史的教育价值以及课程标准所提出的数学的四类价值，我们将课堂上的数学文化内涵分成知识源流、学科联系、社会角色、审美娱乐和多元文化五个维度，具体内容见表1。

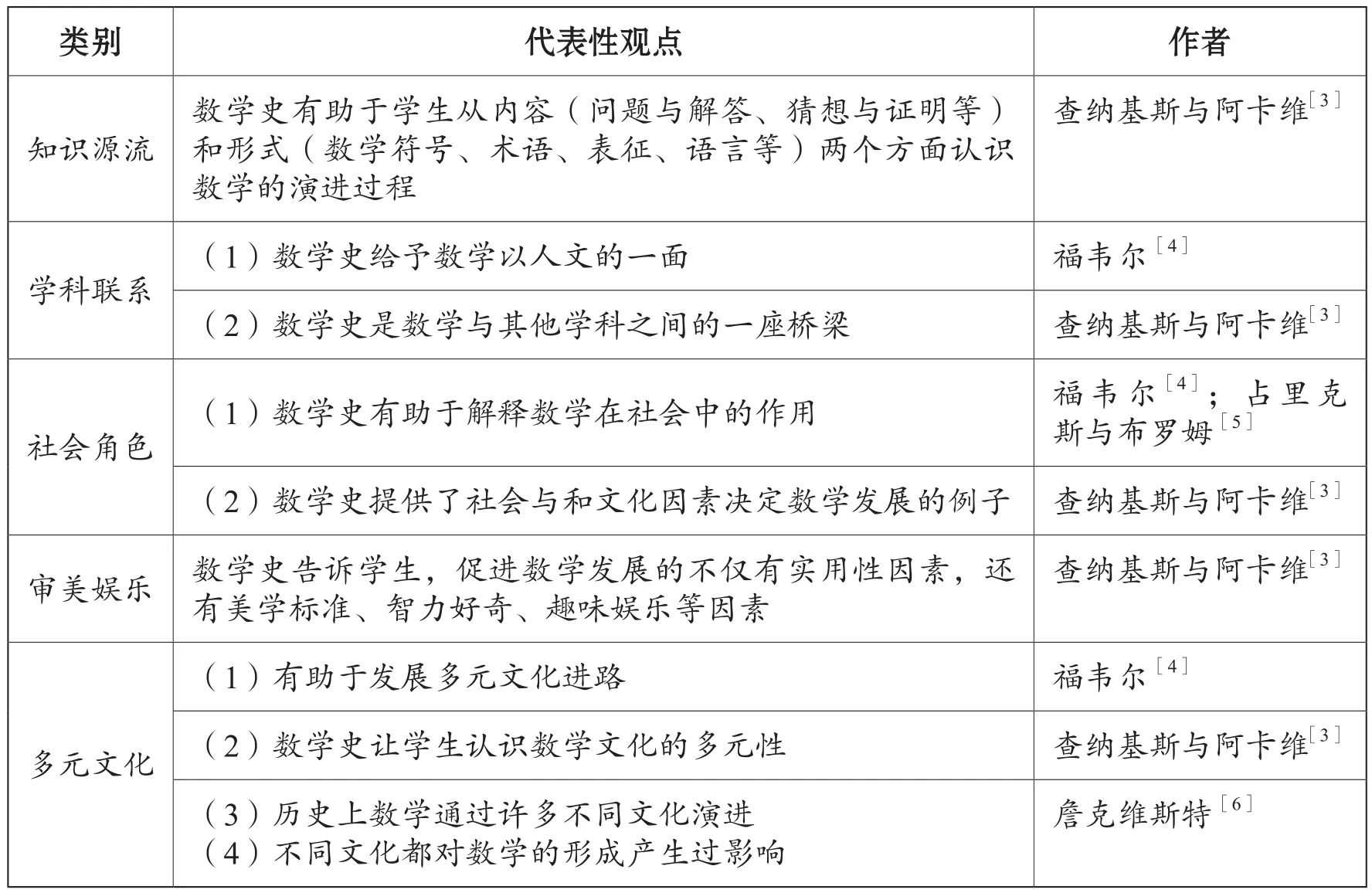
表1 基于数学史的数学文化内涵分类框架

早在19世纪以前，很多文化名人都已对数学的教育价值有过探讨［7］。图1呈现了一些主要的观点。其中，学科基础、现实应用、消遣娱乐分别对应于数学文化五个维度中的学科联系、社会角色和审美娱乐。

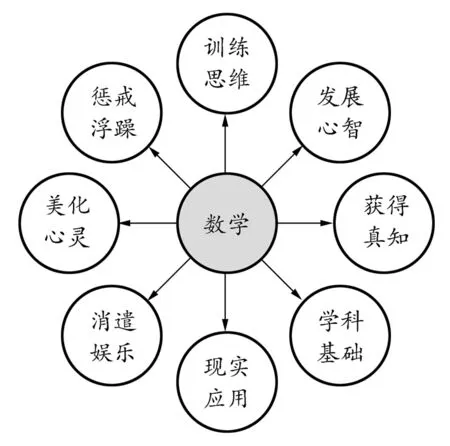
图1 数学的教育价值

五个维度在《标准》中都有涉及。“知识源流”指的是某个知识点的历史发展过程以及相关的人物、事件、思想等。《标准》在必修课的函数主题上，要求“收集函数概念的形成与发展的历史资料，撰写论文，论述函数发展的过程、重要结果、主要人物、关键事件及其对人类文明的贡献”；关于对数函数，要求“收集对数概念的形成和发展的历史资料，撰写论文，论述对数发明的过程以及对数对简化运算的作用”［1］。在必修课的代数与几何主题上，要求“收集几何发展的历史资料，撰写论文，论述几何发展的过程、重要结果、主要人物、关键事件及其对人类文明的贡献”［1］；关于数列，要求“收集我国关于数列方面的研究成果，撰写论文，论述发展的过程、重要结果、主要人物、关键事件及其对人类文明的贡献，例如，以‘杨辉三角'、《四元玉鉴》等重要成果为例”［1］。在选修课的对应主题上，也有类似要求。

“学科联系”指的是数学与其他学科之间的关联。M·克莱因曾将“文化原理”列为数学课程四大原理之一，认为数学教学中应该将数学与其他学科知识联系起来。［8］《标准》在“课程性质”中指出：“数学是自然科学的重要基础，并且在社会科学中发挥越来越大的作用。”［1］在“课程理念”中要求“注重数学文化的渗透，强调数学与生活以及其他学科的联系”［1］；在“教学建议”中要求教师“了解数学与生活、数学与其他学科的联系，创造出符合学生认知规律、有助于提升学生数学核心素养的优秀案例”［1］。

“社会角色”指的是数学对人类文明进步、社会发展所起的重要作用。《标准》在“课程性质”中称：“数学与人类生活和社会发展紧密关联……数学的应用已渗透到现代社会及人们日常生活的各个方面……数学直接为社会创造价值，推动社会生产力的发展。”［1］

“审美娱乐”指的是数学美与趣味数学。《标准》在D课程中设置了“美与数学”，包括“美与数学的简洁”“美与数学的对称”“美与数学的周期”“美与数学的和谐”等。但《标准》几乎没有涉及趣味数学。

“多元文化”指的是不同文明、不同地域在同一数学课题上的成就和贡献。《标准》在“教科书编写建议”中强调：“要把数学文化融入到数学学习内容中，充分体现数学的文化价值，体现数学对于人类文明发展的贡献。在内容中，既要结合数学史适时吸收一些体现中华民族优秀传统文化的素材；也要借鉴异域文化的优秀成分，展现高中数学教科书应有的国际视野。”［1］

三、HPM课例中的数学文化

数学文化内涵与课程标准所说的数学的四类价值之间的联系如图2所示。

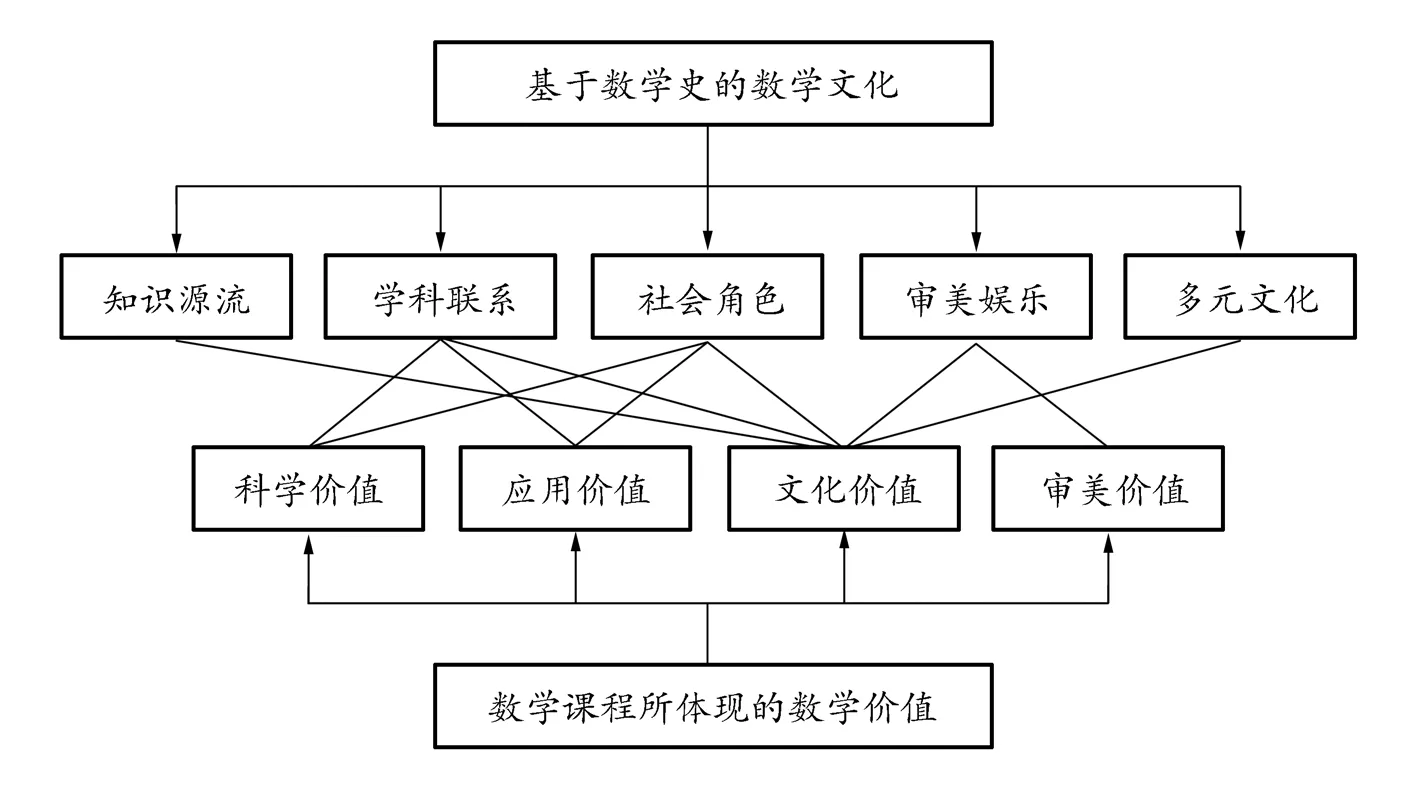
图2 数学文化各维度与数学价值的对应关系

（一）知识源流

在HPM视角下的数学教学中，教师以不同方式运用了有关的数学史料（人物、事件、概念、术语、命题、思想、方法、工具、符号等），这些课例都让学生或多或少地了解、感悟数学知识的源与流。歌德（J. W. von Goethe）云：“一门科学的历史就是这门科学本身。”［9］按照詹克维斯特（Jankvist）的“工具—目标”二元论［6］，数学史本身就是数学学习的目标之一；在课堂上追溯知识之源，是揭示数学的文化价值的重要途径之一。

课例“平方差公式”［10］展示了赵爽的几何方法和他的治学精神；课例“同底数幂的运算”［11］再现了古希腊数学家阿基米德（Archimedes）数沙的方法和他与叙拉古王子的故事；课例“全等三角形的应用”［12］融入了古希腊数学家泰勒斯（Thales）的测量方法并讲述了他的故事；课例“可化为一元一次方程的分式方程”［13］以13世纪斐波那契（L. Fibonacci）的雇工付酬问题来引入新课题；课例“一元二次方程的配方法”［14］采用了阿拉伯数学家花拉子米（al-Khwarizmi）的几何解法；课例“函数的概念”［15］追溯了“函数”概念从解析式定义到变量依赖关系定义的历程以及“函数”一词的来历，等等，这些课例往往都涉及一个人物、一个问题、一种方法、一个主题，使课堂洋溢着文化的芬芳。

（二）学科联系

数学史告诉我们，数学与人类其他知识领域（自然科学、人文与社会科学、艺术等）息息相关，数学史正是沟通数学与其他学科的一座桥梁。因此，数学与其他学科之间联系乃是课堂上数学文化的重要内涵之一。

在课例“勾股定理”［16］中，教师尝试从海涅（H. Heine）的一首诗开始：

真理，她的标志是永恒

暗昧世界始见她的光明

毕氏定理今犹在

恰似初授时的情形

缪斯女神把这光芒馈赠

毕达哥拉斯要把祭礼行

百牛烤熟又切片

难表心中感激之情

从那天起，当它们臆测

又一个真理揭开了面容

在地狱般的圈栏

暴发出一阵阵哀鸣

难阻真理发现者的暴行

毕氏让它们永不得安宁

它们瑟瑟颤抖着

绝望地闭上了眼睛

这首诗表达了诗人对弱者的同情之心，诗中的施暴者正是发现勾股定理（后人称之为“百牛定理”）的毕达哥拉斯学派。教师由此提出问题：究竟是怎样的一个几何定理，能让数学家和牛结下“千古仇怨”呢？

利用文学作品来教数学，是数学教学中体现学科联系的途径之一。体现学科联系的HPM课例富有吸引力，令人耳目一新。

（三）社会角色

数学在人类文明史上扮演着举足轻重的作用，应用的广泛性正是数学的基本特点之一。比利时-美国科学史学者萨顿（G. Sarton）甚至认为，数学史是文明史的核心。数学的“社会角色”，主要指的是数学的应用价值。

荷兰HPM学者范马南（van Maanen）曾将14世纪意大利的一个法律案例用于课堂教学［17］：如图3所示，甲、乙两块土地的主人都想获得洪水过后所产生的肥沃的淤积地，问：两人如何分配这块淤积地？意大利法律教授巴托鲁斯（Bartolus）给出了分配方案：淤积地离谁家原有土地的边界更近，就归属谁家。学生经过探究得出，图中两条边界线所构成角的平分线就是两家各得的淤积地的分界线。接着，将边界线换成圆弧以及更一般的曲线，让学生进一步探究淤积地的分配方法。这是用数学解决法律问题的例子。

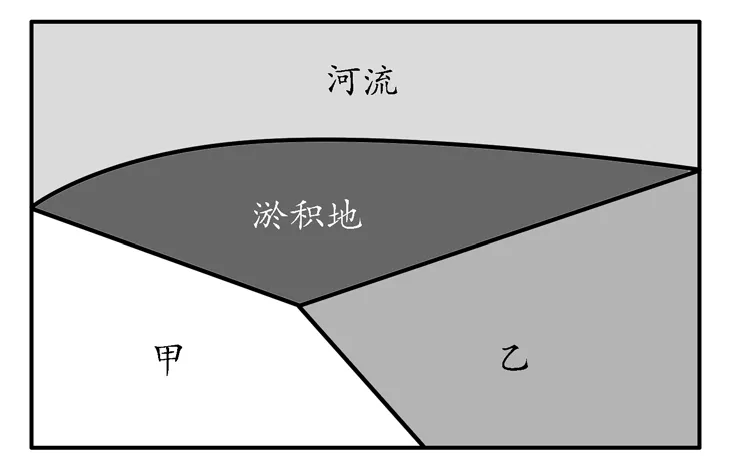
图 3 淤积地分配问题

在课例“相似三角形的应用”［18］中，教师将古希腊萨默斯隧道的设计问题用于课堂教学，深受学生的喜爱。

萨默斯隧道全长1036米，横断面宽和高均为1.8米，被誉为古代水利工程的奇迹。教师在介绍该隧道的基本信息之后，提出问题：公元前6世纪的古希腊人究竟是如何设计隧道的？他们何以能将隧道开凿得如此精准？在学生热烈讨论之后，教师揭开了隧道背后的秘密。如图4所示，隧道的北、南入口分别为A和B。从南入口B出发，在山外筑一条水平的道路BCDEFGHIJ，接近北入口，这条路由若干直线段首尾连接而成，相邻两段互相垂直。再从北入口A筑一条路AK垂直于IJ，垂足为K。过A作CB反向延长线的垂线，垂足为L，连接AB，于是得RtΔALB，利用山外路段的长度，易于算出直角边AL和BL的长度。分别在AK和BC上取点M和N，过点M作AK的垂线段MP，过点N作BC的垂线段NQ，使得PM:AM = QN:BN = AL:BL，于是 RtΔAMP、RtΔBLA、RtΔBNQ两两相似，因此，P、A、B、Q四点共线。因此，只要在P、Q两处放置标志物，南北两个工程队在开凿过程中始终能看到标志物，即能确保方向正确了。

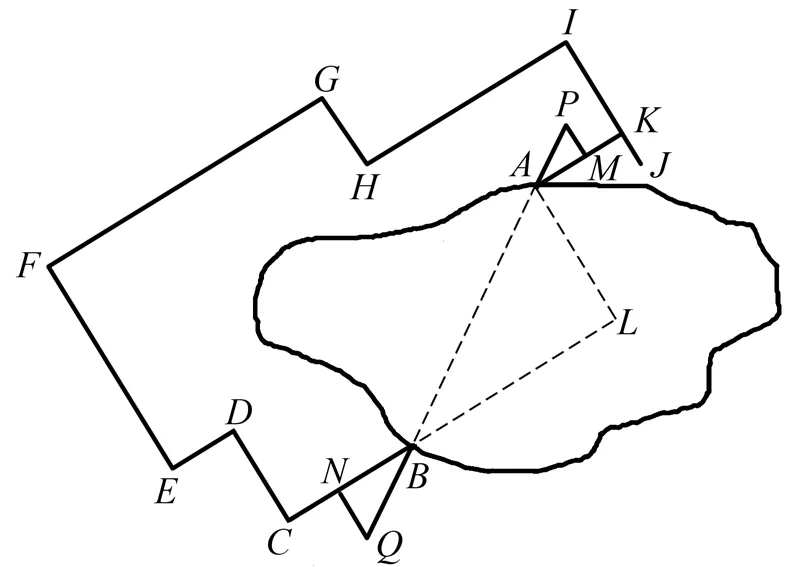
图4 古希腊数学家海伦所记载的隧道设计方法

海伦所记载的上述隧道设计方法让学生惊叹几何学的应用价值和神奇力量，真切感受到了数学与现实生活之间的密切联系，深刻体会到了数学的社会角色。

（四）审美娱乐

世界因数学而美丽，数学因教育而精彩。虽然数学美无处不在，但这种美是针对具备一定鉴赏力的学生而言的。而学生对于数学美的鉴赏，需要教师在课堂上创造机会、并给予引领。在课例“字母表示数”［19］中，教师用英国幽默作家杰罗姆（J. K. Jerome）《懒人懒办法》中的一段文字来说明字母表示数的意义：

“12世纪的青年堕入情网，你可别指望他会后退三步，凝视情人的眼睛，然后告诉他：你太美了，美得简直不像活人。他会说他要到外边去看看。倘若正好碰上那么一位仁兄，并打破他的脑袋——我指的是另外那个家伙的脑袋，这就说明他——前一个人的情人是个漂亮姑娘。但要是另一个家伙打破他的头——不是他自己的，这是你知道的，而是另一个家伙的——另一个家伙是对第二个家伙而言的，这就是说，因为事实上另一个家伙仅仅对于他来说是另一个家伙，而不是第一个家伙——好了，如果他的头被打破，那么他的女孩——不是另一个家伙的，而这个家伙——你瞧，如果A打破了B的头，那么A的情人就是一个漂亮女孩；反之，如果B打破了A的头，那么A的情人就不是个漂亮女孩，而B的情人才是。”

尽管这段文字无关数学，但从侧面展示了数学的简洁之美。而在课例“完全平方公式”中，教师介绍了古希腊数学家欧几里得（Euclid）在《几何原本》卷二中给出的命题：“任意分一线段成两段，则整段上的正方形等于两分段上的正方形与两分段所构成矩形的两倍之和。”让学生感受今日符号语言的简洁之美和对称之美。

历史上的趣味数学问题是HPM课例的重要素材。在课例“一元一次方程”中，教师运用了《希腊选集》中的丢番图的墓志铭；在课例“二元一次方程组的概念”中，教师采用了古希腊数学家欧几里得的著名趣味问题：“骡子和驴驮着酒囊行走在路上，为酒囊重量所压迫，驴痛苦地抱怨着，听到驴的怨言，骡子给她出了这样一道题：“妈妈，你为何眼泪汪汪，满腹牢骚，抱怨的应该是我才对呀！因为，如果你给我一袋酒，我负的重量就是你的2倍；若你从我这儿拿去一袋，则你我所负重量刚好相等。”好心的先生，数学大师，请你告诉我，他们所负酒囊各几袋？”

历史上的趣味问题仿佛陈年佳酿，历久弥香。学生仿佛穿越时空，与古人一起感受数学带来的愉悦。

（五）多元文化

历史上不同时空的数学家对于同一个数学主题往往都做出了各自的贡献，数学史揭示了数学文化的多元性。因此，“多元文化”构成了数学文化的重要内涵。

在课例“一次方程组的应用”［20］中，教师运用了古代中国、古巴比伦、中世纪欧洲的数学问题。学生认为，古代数学问题让他们体会到古代不同文明的数学文化，开阔了他们的视野。在课例“分数指数幂”［21］中，教师展示了14世纪法国数学家奥雷姆（N. Oresme）、16世纪荷兰数学家斯蒂文（S. Stevin）、17世纪荷兰数学家吉拉德（A. Girard）、英国数学家牛顿（I. Newton）等对分数指数幂概念和符号表达的贡献（见图5），呈现了多元文化。

图5 分数指数幂概念和符号的历史演进

四、结语

以上我们看到，数学文化内涵的五个维度——知识源流、学科联系、社会角色、审美娱乐、多元文化在HPM课例中都有体现。但在实践中，不同维度的利用并不均衡。HPM视角下的数学教学，是指以解决某个教学问题为主旨，借鉴、运用数学史的课堂教学。因此，所有的HPM课例都会涉及知识源流。HPM课例力求凸显知识的必要性，因而往往会体现数学的社会角色。但在学科联系、审美娱乐、多元文化三个维度上，已有的课例做得并不理想。无疑，要在教学中深刻、全面体现数学的科学价值、应用价值、文化价值和审美价值，优化数学史的教育价值，我们还需要在已有课例研究的基础上开展更深入、系统的数学史文献研究和实践研究。