基于G-Q的K-S异方差检验方法
张晓琴,牛建永,李顺勇
(山西大学 数学科学学院,山西 太原 030006)
0 引言
在经典的线性回归模型中,常用最小二乘估计(OLS)法对线性回归模型进行估计,从而对线性回归模型进行拟合和预测。其中,同方差性是经典线性回归模型中的一个重要假设,然而大部分线性回归模型是不满足这个假设的。当线性回归模型存在异方差时,如果仍然使用OLS估计模型的参数,将会产生一些不良后果:比如,参数的估计虽是无偏的,但不是最佳线性无偏估计;参数的显著性检验失效等。另外,若由异方差检验得出的判断出现失误还有可能会导致一定的损失。因此采取适当的方法对线性回归模型进行异方差检验就具有重要意义。
常用的检验异方差的方法有图示法、斯皮尔曼(Spearman)的秩相关系数检验[1-2]、格莱舍尔(Glejser)检验[3]、戈德菲尔德匡特(Goldfeld-Quandt)检验[4]、怀特(White)检验[5]、帕克(Park)检验[6]、布罗施帕甘戈弗雷(BPG)检验[7-8]和ARCH检验[9]等。
其中,G-Q检验是经典的异方差检验方法。但在一元线性回归模型中使用G-Q检验,通常要求误差项的方差与自变量之间存在递增或递减关系,若两者之间不具有这种关系,使用G-Q检验有可能导致错误的判断,然而这个假设条件常常被忽略;当在多元线性回归模型中若使用G-Q检验,其思想是先把多元线性回归模型的异方差检验转为对每一个一元线性回归模型分别进行G-Q检验,然后根据G-Q检验结果来判断多元线性回归模型是否存在异方差。由于多元线性回归模型并不等于多个一元线性回归模型的简单相加,因此,根据一元线性回归模型的G-Q检验结果,并不能准确判断多元线性回归模型是否存在异方差。本文针对上述现象进行了研究。
1 基本知识
1.1 异方差模型
经典线性回归模型矩阵形式为:
(1)
其中,y是n维列向量,β是p+1维向量,X是n×(p+1)列满秩矩阵,ε表示线性回归模型的随机误差项向量。
1.2 G-Q检验
由于G-Q检验多用于一元线性回归模型的异方差检验,因此,下面先基于一元线性回归模型对G-Q检验加以简单介绍,然后再介绍在多元线性回归模型中使用G-Q检验的思想。
假定一元线性回归模型为:
(2)
模型(2)满足除同方差性外的所有经典假设,而且假设模型误差项的方差与自变量之间存在递增或递减关系。
考虑如下假设检验问题:
不全相等。
(3)
经典的G-Q检验步骤[4-5]为:
① 把解释变量的n个样本观察值x1,x2,…,xn由从小到大进行排序,排序后顺序不妨记为x(1)≤x(2)≤…≤x(n),相应地,因变量的n个观察值y1,y2,…,yn排序为y(1)≤y(2)≤…≤y(n).

③ 分别对前L个观测值和后L个观测值各拟合一个线性回归方程,并计算各自的残差平方和,记为RSS1和RSS2,其中,RSS1代表由前L个观测值所拟合的线性回归模型残差平方和(小方差组),而RSS2代表由后L个观测值所拟合的线性回归模型残差平方和(大方差组),各有L-k个自由度,其中k是包括常数项在内的参数个数。
④ 构造统计量
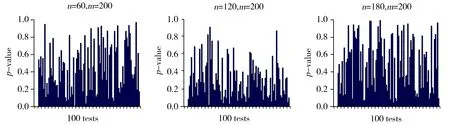
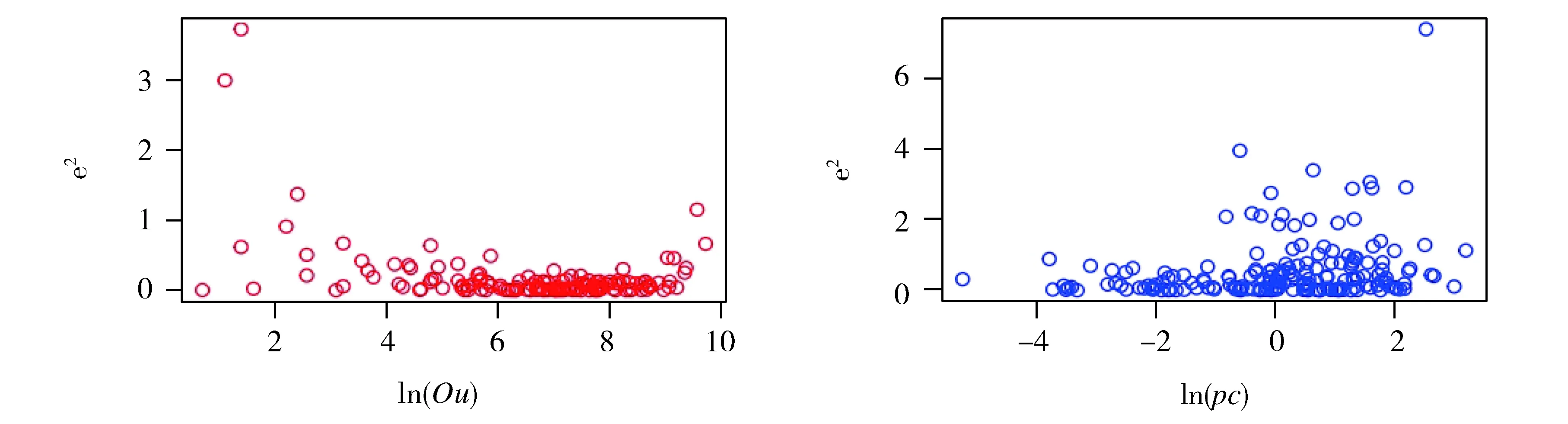
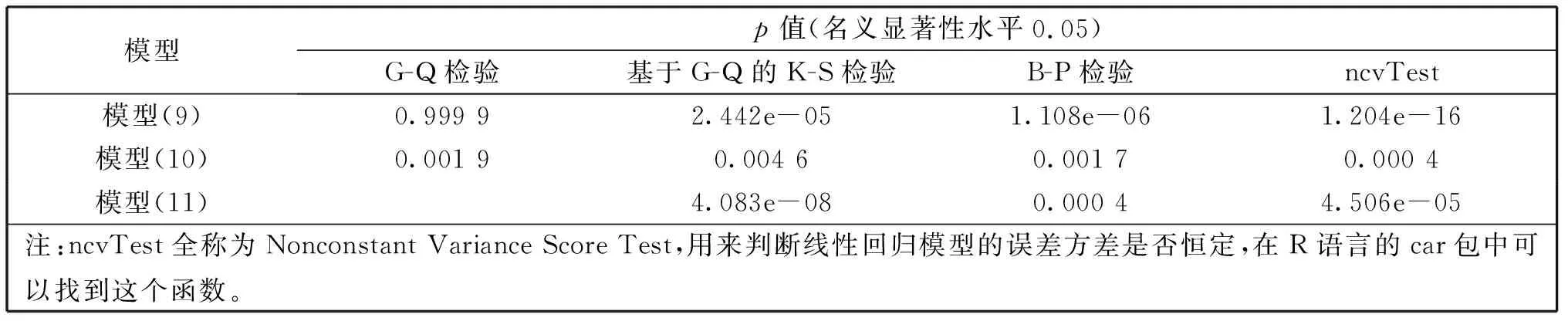
在(3)中原假设成立的条件下,统计量Fa服从自由度分别为γ1=L-k和γ2=L-k的F分布,其临界值为Fα(γ1,γ2)(α为给定显著性水平)。当Fa 当G-Q检验用在多元线性回归模型中时,其思想是先把多元线性回归模型转化为多个一元线性回归模型,并分别对其进行G-Q检验,然后根据G-Q检验结果进行判断,若所有一元线性回归模型均不存在异方差,则可以说明多元线性回归模型不存在异方差,否则存在异方差性。事实上,在多元线性回归模型的异方差检验中,并不经常使用G-Q检验。 Kolmogorov-Smirnov检验[14-20](K-S检验)是一种拟合优度检验,用来根据一个未知分布的单一随机样本,检验其分布函数是否是来自某一具体的分布。这一检验方法是以随机样本数据的经验分布函数与已知具体分布比较,若两者之间的差距不显著,则推论该样本取自某具体分布。其思想如下: 提出如下原假设和备择假设: H0:随机样本所来自的总体分布服从某具体分布VSH1:样本所来自的总体分布不服从某特定分布 F0(x)表示某具体分布的分布函数,Fn(x)表示单一随机样本的经验分布函数。设D为F0(x)与Fn(x)差距的最大值,即 当实际观测D 基于上述经典的G-Q检验思想和步骤,经典的G-Q检验法有以下不足: 在一元线性回归模型的异方差检验中,假设误差项的方差与自变量之间不存在递增或递减关系,若使用G-Q检验法对回归模型进行异方差检验,就有可能导致错误的判断。而且在多元线性回归模型的异方差检验中,进行G-Q检验是先把多元线性回归模型转化为多个一元线性回归模型,然后根据对多个一元线性回归模型进行G-Q检验的结果,来判断多元线性回归模型是否存在异方差。由于多元线性回归模型并不等同于多个一元线性回归模型的简单相加,因此,根据每一个一元线性回归模型的G-Q检验结果,并不能判断多元线性回归模型是否存在异方差,也即是在多元线性回归模型的异方差检验中,G-Q检验并不是有效的检验方法。 针对G-Q检验的局限性,本文基于G-Q检验思想,采用 K-S检验方法来进行线性回归模型的异方差检验,该方法简称为基于G-Q的K-S异方差检验。其基本原理如下:将样本量为n的样本分为两部分,两部分样本量分别为n1和n2。由模型(1)假设这两部分的回归模型矩阵形式分别为: (4) (5) (6) 重复上述过程m次,则可以得到m个随机抽样统计量Fb的样本观测值F1,F2,…,Fm。根据K-S检验,比较由样本观测值F1,F2,…,Fm形成的经验分布与自由度分别为n2-p-1和n1-p-1的F分布之间是否存在显著性差异。若两者之间存在显著性差异,则说明线性回归模型存在异方差,否则不存在异方差。 下面证明上述定理。 ni-rank(Xi)=ni-p-1. 下面给出具体的检验步骤: ③ 根据K-S检验,比较由样本观测值F1,F2,…,Fm所形成的经验分布与自由度分别为n-p-1和n-p-1 (或n-p-1和n-p)的F分布是否有显著性差异。若有显著性差异,则拒绝(3)中的原假设,否则不拒绝。 本文数值模拟分为一元和多元线性回归模型的异方差检验数值模拟两部分,下面先进行一元线性回归模型的异方差检验数值模拟,然后再进行多元线性回归模型的异方差检验数值模拟。 假设一元线性回归模型为: yi=β0+β1xi+εi,i=1,2,…,n. (7) 由于一次基于GQ的K-S检验可能具有一定的偶然性,因此,本文进行了100次基于G-Q的K-S检验,每一次检验结果均用p值表示(给定的显著性水平为0.05,下同)。情形1的模拟检验结果分别如图1至图3所示。从图中可以看出图1至图3中p值小于0.05的个数分别为3,4,3(与图1的排列顺序一致,下同);2,3,3;4,4,3,则情形1模拟检验结果说明:有95%以上的可信度可以认为,模型(7)不存在异方差;情形2的模拟检验结果p值大于0.05的个数均为0个,结果说明:有100%可信度可以认为,模型(7)存在异方差。由于情形2的模拟检验结果p值的真实值的数量级小于10-5,在图中几乎显现不出来为了节省篇幅,本文没有给出情形2下的模拟检验结果图。 注:图中横轴表示进行基于GQ的K-S检验次数100次,纵轴表示每次进行检验得出的p值,n表示原始样本容量,m表示进行200次随机抽样(下同)。Fig.1 Charts of frequency distribution of p-value in case 1 with x~N(0,9)图1 在情形1,自变量x~N(0,9)下p值的频数分布图 Fig.2 Charts of frequency distribution of p-value in case 1 with x~exp(10)图2 在情形1,自变量x~exp(10)下p值的频数分布图 Fig.3 Charts of frequency distribution of p-value in case 1 with x~U(0,10)图3 在情形1,自变量x~U(0,10)下p值的频数分布图 假设多元线性回归模型为: yi=β0+β1x1i+β2x2i+β3x3i+εi,i=1,2,…,n. (8) 这部分模拟同样进行了100次基于GQ的K-S检验,检验结果用p值表示,在情形3和情形4下的检验结果分别如图4至图6和图7至图9所示。从图中可以看出,图4至图6中p值小于0.05的个数分别为2,3,4;5,2,3;2,3,1,则情形3的模拟检验结果说明:有95%以上的可信度可以认为模型(8)不存在异方差;图7至图9中p值大于0.05的个数分别为6,0,0;2,1,0;1,2,3,则情形4的模拟检验结果说明:有94%以上的可信度可以认为,模型(8)存在异方差。 Fig.4 Charts of frequency distribution of p-value in case 3 with x1,x2,x3~exp(5)图4 在情形3,自变量x1,x2,x3~exp(5)下p值的频数分布图 Fig.5 Charts of frequency distribution of p-value in case 3 with x1,x2,x3~U(0,10)图5 在情形3,自变量x1,x2,x3~U(0,10)下p值的频数分布图 Fig.6 Charts of frequency distribution of p-value in case 3 with x1~U(0,1),x2~exp(5),x3~P(4)图6 在情形3,自变量x1~U(0,1)x2~exp(5),x3~P(4)下p值的频数分布图 Fig.7 Charts of frequency distribution of p-value in case 4 with x1,x2,x3~exp(5)图7 在情形4,自变量x1,x2,x3~exp(5)下p值的频数分布图 Fig.8 Charts of frequency distribution of p-value in case 4 with x1,x2,x3~U(0,10)图8 在情形4,自变量x1,x2,x3~U(0,10)下p值的频数分布图 注:图中出现p值为是指p值的真实值的数量级小于10-5,在图中几乎显现不出来,因此,本文为了简便起见,把结果记为0。Fig.9 Charts of frequency distribution of p-value in case 4 with x1~U(0,1)x2~exp(5),x3~P(4)图9 在情形4,自变量x1~U(0,1)x2~exp(5),x3~P(4)下p值的频数分布图 根据一元和多元线性回归模型异方差检验的大量数值模拟结果可以得出:基于G-Q的K-S异方差检验法具有一定的可行性和可靠性。 本文实证分析分为一元和多元线性回归模型异方差检验实证分析两部分。其中,第一部分为一元线性回归模型异方差检验实证分析,第二部分为多元线性回归模型异方差检验实证分析。 一元线性回归模型异方差检验实证分析采用的两个数据集分别为:Marc Nerlove 1963年论文中的Nerlove(1963)数据[21]中的ProductionsCosts (PC)和Outputs (Ou)两个变量和R语言AER包里的Journals数据中的subs (su)及price与citations的比值形成的新变量(pc)两个变量(括号里的部分为简写)。根据实际问题研究的需要,对变量PC,Ou,su和pc均取自然对数,取对数后的变量分别记作ln(PC),ln(Ou),ln(su)和ln(pc),下面分别检验如下两个线性回归模型 ln(PC)i=β0+β1ln(Ou)i+εi,i=1,2,…,145. (9) ln(su)i=β0+β1ln(pc)i+εi,i=1,2,…,180. (10) 是否存在异方差。 根据已知样本数据分别对模型(9),(10)进行线性回归,其残差平方(用e2表示)与自变量ln(Ou)和ln(pc)的散点图如图10所示。从图中可以看出,模型(9)的残差平方与自变量ln(Ou)不存在递增或递减关系(先有递减趋势,再保持稳定,后又有递增趋势);模型(10)的残差平方与自变量ln(pc)有明显的递增趋势,而且模型(9)和模型(10)均有可能存在异方差。 Fig.10 Scatter plot between independent variable and residual squares图10 残差平方与自变量的散点图 下面对模型(9),(10)分别进行统计检验,使用的检验方法有G-Q检验、基于G-Q的K-S检验、B-P检验和ncvTest检验。检验结果如图11(a),(b)和表1所示。在表1中,模型(9)与模型(10)的G-Q检验的p值分别为0.999 9(大于0.05)和0.001 9(小于0.05),则根据G-Q检验结果说明:模型(9)不存在异方差,模型(10)存在异方差;从图11(a)和(b)中可以看出,实线和虚线的趋势不一致,而且在表1中使用基于G-Q的K-S检验的p值分别为2.442e-05和0.004 6,两者均小于0.05,则根据基于G-Q的K-S检验结果说明:模型(9)和模型(10)均存在异方差。为了进一步说明异方差检验的可靠性,本文使用了B-P检验和ncvTest检验。其中,B-P检验和ncvTest检验的p值均小于0.05,说明模型(9)和模型(10)均存在异方差。 模型p值(名义显著性水平0.05) G-Q检验基于G-Q的K-S检验B-P检验ncvTest 模型(9)0.999 92.442e-051.108e-061.204e-16 模型(10)0.001 90.004 60.001 70.000 4 模型(11)4.083e-080.000 44.506e-05注:ncvTest全称为Nonconstant Variance Score Test,用来判断线性回归模型的误差方差是否恒定,在R语言的car包中可以找到这个函数。 在模型(10)中,由与G-Q检验、基于G-Q的K-S检验、B-P检验和ncvTest检验得出的结论一致,说明模型(10)存在异方差。在模型(9)中,G-Q检验与基于G-Q的K-S检验、B-P检验和ncvTest的结果不一致,而基于G-Q的K-S检验、B-P检验和ncvTest检验结果一致,则可以说明模型(9)存在异方差,而不是存在同方差。因此,在模型(9)中,若使用G-Q检验,则会做出错误的判断。 通过一元线性回归模型异方差检验实证分析表明:在一元线性回归模型异方差检验中,使用G-Q检验法需要先判断线性回归模型的残差平方和自变量之间是否具有明显的递增或递减关系。若两者之间存在这种关系才能继续使用G-Q检验法,否则会做出错误的判断。而采用基于G-Q的K-S检验则没有上述条件的制约,而且检验结果具有一定的可行性和可靠性。 多元线性回归模型异方差检验实证分析数据来自2013年中国31个省(自治区,直辖市)的居民消费水平(元),地区生产总值(亿元),现金可支配收入(元)和地区总人口(万人)等4个变量的数据[22]。记变量居民消费水平为因变量y,地区生产总值,现金可支配收入和地区总人口分别为自变量x1,x2,x3。下面检验如下线性回归模型 yi=β0+β1x1i+β2x2i+β3x3i+εi,i=1,2,…,31 (11) 是否存在异方差。 在检验前,先对数据进行标准化,消除由于量纲不同对分析所造成的误差影响。下面使用基于G-Q的K-S检验、B-P检验和ncvTest检验对模型(11)进行统计检验。检验结果如图11(c)和表1所示。在图11(c)中,实线和虚线的趋势明显不一致,而且在表1中使用基于G-Q的K-S检验法进行异方差检验的p值为4.083e-08,小于0.05,则说明模型(11)存在异方差。同时,B-P检验和ncvTest检验的p值分别为0.000 4和4.506e-05,两者均小于0.05,同样得出模型(11)存在异方差。因此,多元线性回归模型异方差检验实证结果表明:在多元线性回归模型异方差检验中,基于G-Q的K-S检验法具有一定的可行性。 根据大量数值模拟结果得出,使用基于G-Q的K-S检验法进行异方差检验具有一定的可行性,实证分析中分别以一元和多元线性回归模型为例进行了异方差检验。在一元线性回归模型中,使用G-Q检验法、基于G-Q的K-S检验法以及作为辅助检验方法的B-P检验和ncvTest检验分别进行了异方差检验,得出了若模型的误差平方与自变量不具有正(负)相关的关系,使用G-Q检验法会导致错误判断;在多元线性回归模型中,分别使用了基于G-Q的K-S检验、B-P检验和ncvTest检验对多元线性回归模型进行异方差检验,检验结果说明基于G-Q的K-S检验适用于多元线性回归模型的异方差检验。通过实证分析,表明基于G-Q的K-S检验法具有一定的可行性和可靠性。事实上,任何理论方法都不是完美的,使用该方法同其他检验方法一样也只能检验出模型是否存在异方差,仍然不能具体检验出引起异方差的自变量,因此在这方面还可以进行更深入的研究。1.3 K-S检验
2 基于G-Q的K-S异方差检验方法
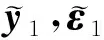




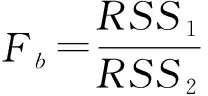
3 数值模拟和实证分析
3.1 数值模拟
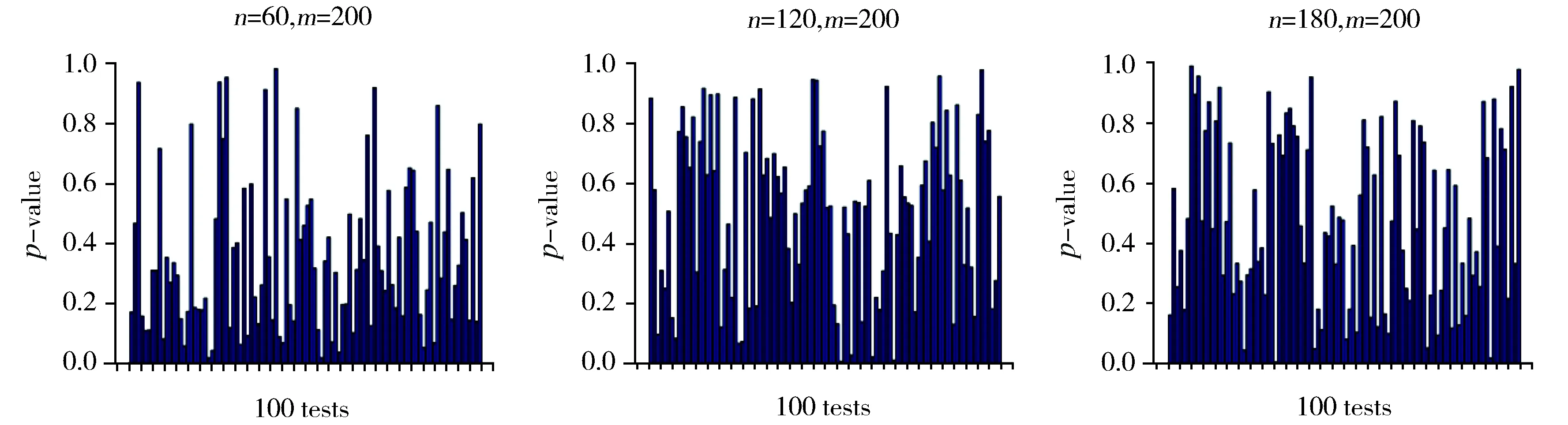
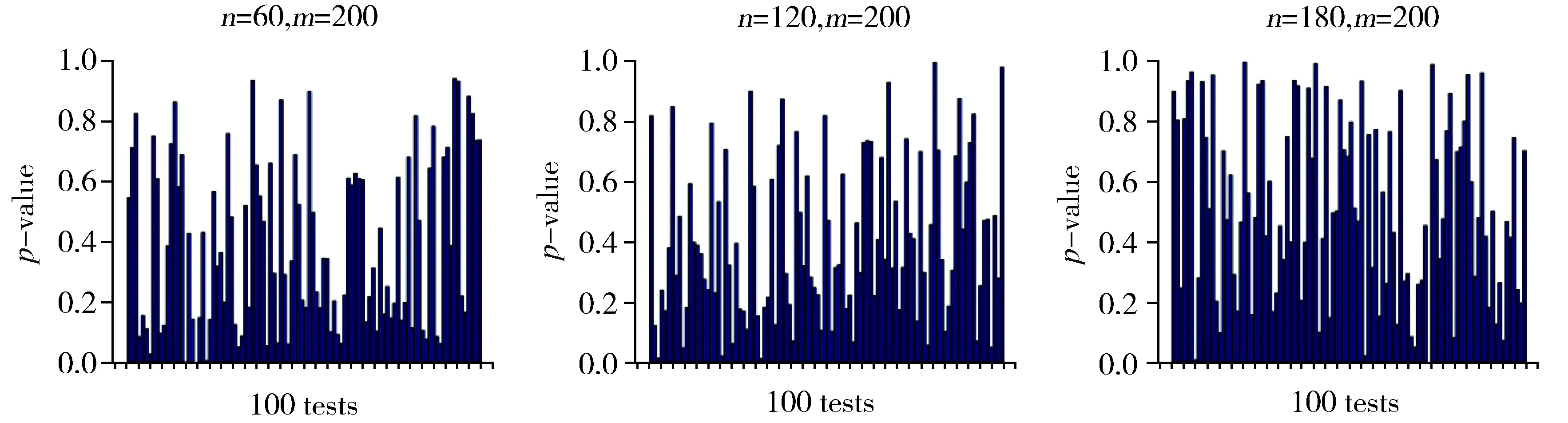
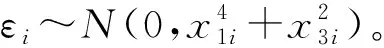





3.2 实证分析
4 结论

