基于模糊决策的非即时衰减品动态定价

王永昭

(1.安阳师范学院 数学与统计学院,河南 安阳 455000;2.天津大学 管理与经济学部,天津 300072)

0 引言

随着经济的快速发展,顾客自我意识的不断提高,需求越来越趋于个性化。同时,市场的激烈竞争使得产品更新换代越来越快,产品的生命周期越来越短。销售市场中把这种容易腐烂变质或者消费者消费偏好变化而引起销售周期缩短的产品称之为易逝品。易逝品具有较强时效性和需求波动性,已成为供应链管理研究的热门话题。然而,在实际生活中,有很多易逝品在库存初始时期(保鲜期)价值保持不变,之后才会发生衰减,称之为非即时衰减品[1]。例如某些果蔬,会在初始的一段时间内保持较高的新鲜度。如果忽略了产品非即时衰减的特性,会导致成本高估,使得零售商做出错误决策,非即时衰减品吸引了越来越多学者的关注和研究[2-4]。

定价问题是非即时衰减品的一个重要研究领域。定价作为现代企业最重要的策略之一,是企业增加收益的主要手段[5]。因此,合理定价是现代公司追求高投资回报的普遍方式。动态定价有别于传统的静态定价,是指经营者敏感地感受市场需求的波动及时调整销售价格以达到收益最大化目的。科技的飞速发展为动态定价提供了技术便利和成本优势,推动了动态定价的实践与应用。 Kincaid和Darling[6]早在1963年就开始研究易逝品连续时间的动态定价问题。Wang等[7]运用极大值原理把动态定价问题扩展到了非即时衰减品中。近年来,越来越多的研究展示了动态定价的有效性和优越性[8-9]。

企业在销售过程中往往面临着市场和消费者需求的高度不确定性,以及消费者的消费行为的复杂性,因此把这些因素考虑到定价模型中非常有必要。以往的动态定价研究中往往假设消费者满足理性人假设,例如文献[10-11],然而在实际的生活中,存在大量的非理性消费者这些很大程度上影响了企业的定价策略制定。本文参考文献[12]引入模糊函数来刻画消费者购买产品的可能性,更符合实际情况。

考虑到产品非即时衰减的特性,本文构造了基于消费者购买决策的模糊函数,针对价值判断异性的消费者,建立销售周期和初始库存确定的非即时衰减品动态定价模型。在零售商收益最大化的目标下,运用变分法求解模型,得到最优动态定价函数。最后进行了数值模拟和主要参数的灵敏度分析,得到了一些重要的管理学启示。

1 动态定价模型

1.1 模型描述

在本文考虑一个垄断的零售商在一定时间段[0,T]内销售单一非即时衰减品(如水果、农蔬产品等)的动态定价问题。此时,非即时衰减品是指在保险期内价值不变,之后随着时间价值发生衰减的产品,保鲜期td为确定常量。

为保证模型的合理性及正确性,做出如下假设:

假设1:初始库存I。在整个销售期内,零售商不存在补货行为,该批次的产品剩余量为0时即销售期结束。不同于别的商品,非即时衰减品生命周期较短,销售期末残值很小,几乎为零,所以零售商一般采取库存清空策略。

假设2:产品的成本为固定常数。为简化模型不失一般性,整个销售周期不考虑销售价格的菜单成本。非即时衰减品采摘或生产流程固定,库存运营管理体系成熟,产品成本短期内受外界影响较小,故刻画为固定常数。

假设3:参考文献[12],在整个销售期内顾客以泊松过程到达商店,平均到达率为λ(t)。

假设4:销售市场被充分细化,消费者对产品价值判断异性。假设消费者对非即时衰减品价值判断V(t)满足

(1)

其中,V为消费者保留价值,服从区间[a,b]上的既定连续分布F,密度函数为f。在[0,td]内产品价值保持不变,消费者对产品价值判断异性。在[td,T]内可以从两方面解释,一方面忽略时间因素,消费者价值判断和前一阶段一致;另一方面非即时衰减品对时间的敏感性,消费者的保留价值是随时间递减的,此处假设为指数递减[7],α为价值衰减因子,用来描述价值衰减速度。

假设5:以往研究主要集中在理性消费者做出购买决策当且仅当其能获得最大的剩余价值。然而,在实际生活中有很多非理性消费者[13]:商品的最大剩余价值大于消费者价值判断时不一定购买,只是购买的可能性会增大。为了刻画这种情况,本文参考文献[12]引入模糊函数如下,

(2)

上式刻画了消费购买产品的概率,描述了消费者的决策过程,其中p(t)为产品t时刻的价格。

1.2 模型建立

考虑消费者模糊决策过程和价值判断异性特点,在销售初期[0,td]产品销售量为

(3)

在销售第二阶段[td,T],产品销售量为

(4)

为保证库存和销售价格的非负性,需满足如下约束

Q1(t)+Q2(t)≤I，

p(t)≥0.

(5)

基于上述假设和分析,构建初始库存水平和销售周期给定情况下零售商利润J最大的最优控制模型:

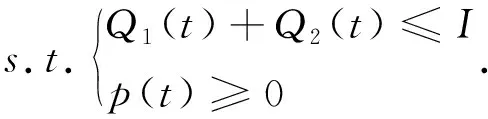
(6)

1.3 模型求解

为了得到更多的管理学启示,下面假设整个销售期消费者的平均到达率为常数λ。原问题的求解可看作泛函求极值问题,由于原问题可分为[0,td]和[td,T]时间段定价问题,且这两个阶段定价相互独立,因此原问题转换为这两个阶段的约束条件不变的最优控制问题。

(7a)

(7b)

利用变分法,分别构造拉格朗日函数为

(8a)

(8b)

其中,μ1,μ2为拉格朗日乘子。因此,欧拉方程可表示为

(9)

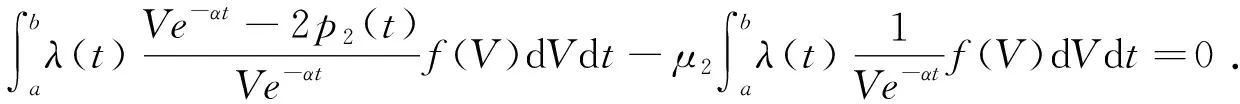
(10)

分别计算得

(11)

(12)

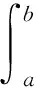
为了求解最优定价,可将原始不等约束简化为

Q1(t)=w,Q2(t)=I0-w.

(13)

其中,w为待定的第一阶段销售量。I0满足下式

(14)

将式(9)、(10)代入以上约束条件可得

(15)

(16)

其中,A=(eα(T-td)-1)/α.

将上式代入式(11)和(12),易得

(17)

(18)

以上可以看出,在第一阶段由于产品处于保鲜期,零售商采取了静态定价策略;然而,当第二阶段产品价值开始衰减,则采用动态定价策略来保持利润。

同时注意到,第一阶段的销售量w取不同值,产品在两个阶段的价格是不一样的。因此,为了求解最优的w,将式(17),(18)代入式(6),并求导可得

(19)

结合上式和式(17)、(18)代入总利润函数,并对其求导,可得

(20)

将上式代入式(17)、(18),得到最优定价策略:

当I<λT/2时

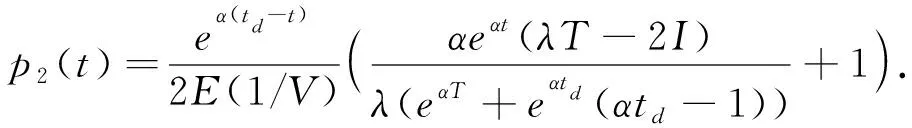
(21)

当I≥λT/2时

(22)

以上可以看出,在第一阶段产品的非即时衰减的特性使得第一阶段采取静态定价策略,而第二阶段采取动态定价策略,结合(21)和(22)式可以发现产品定价遵循阈值策略,当初始库存较低时,定价与顾客平均到达率、衰减因子、保鲜期长度和销售周期有关;而当初始库存很高时,定价仅与衰减因子、保鲜期长度有关。

2 数值分析

通过数值算例对价值衰减因子α,产品保鲜期td,初始库存量I,产品销售周期T等主要参数进行灵敏度分析。

参考文献[5]将该定价模型的基本参数设定为:I=100;λ=10;a=110;α=0.05;b=90;td=20;T=90;

考虑价值衰减因子的变化,得到如图1所示的连续价格曲线。可以看出,在保鲜期内零售商采取静态定价策略,这是由于在库存容量相对充足的条件下,产品价值并未发生变化使得顾客对产品的价值期望不变,为了增加销量,零售商不会轻易变动价格。而保鲜期过后,产品价值成指数下降趋势,为了使价格合理地匹配不断衰减的产品价值,满足消费者预期,零售商采取了动态的降价销售策略。随着衰减因子的不断变大,产品的衰减速度逐渐加快,产品在整个销售期内的价格越来越低,容易发现产品的销售总利润也将会降低。因此,企业可以通过增加产品保鲜方面的投入,如建设冷库,改用冷链运输等措施,降低产品衰减速度来提高利润。

图2描述了保鲜期的变化对产品定价的影响,从图中容易发现随着保鲜期的延长,两阶段的价格均有所上升,这是由于随着产品保持初始价值的时间变长,零售商进行高价销售的时间延长,进而销售利润提高,这在计算结果里也得到了验证。因此,对于采购非即时衰减品时,如水果等,应该选择品相和新鲜度较好的产品,这与实际情况吻合。

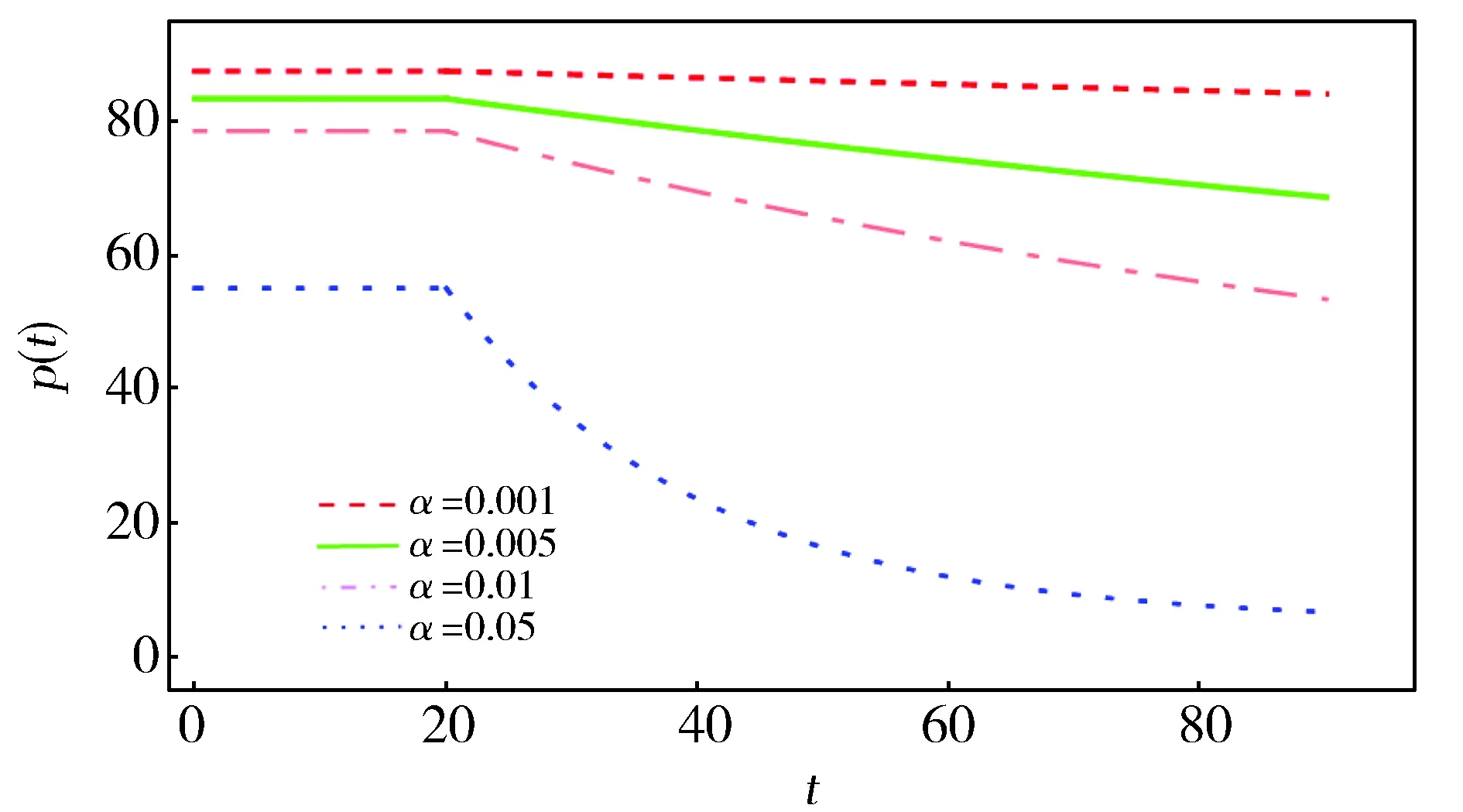
Fig.1 Optimal pricing changes with different attenuation factor图1 最优定价随衰减因子变化图

Fig.2 Optimal pricing changes with different fresh time图2 最优定价随保鲜期变化图

图3展示了不同的初始库存情况下零售商的定价策略,随着初始库存的增大,企业面临有限期内销售完产品的压力,采取了撇脂定价策略以保证利润最大化。但是当库存满足I≥λT/2时,即大于等于450时,零售商的定价策略不变,这时产品到销售期末会有部分剩余,这是因为如果要把所有产品销售完就必须进一步降低价格,进而总利润将会下降。

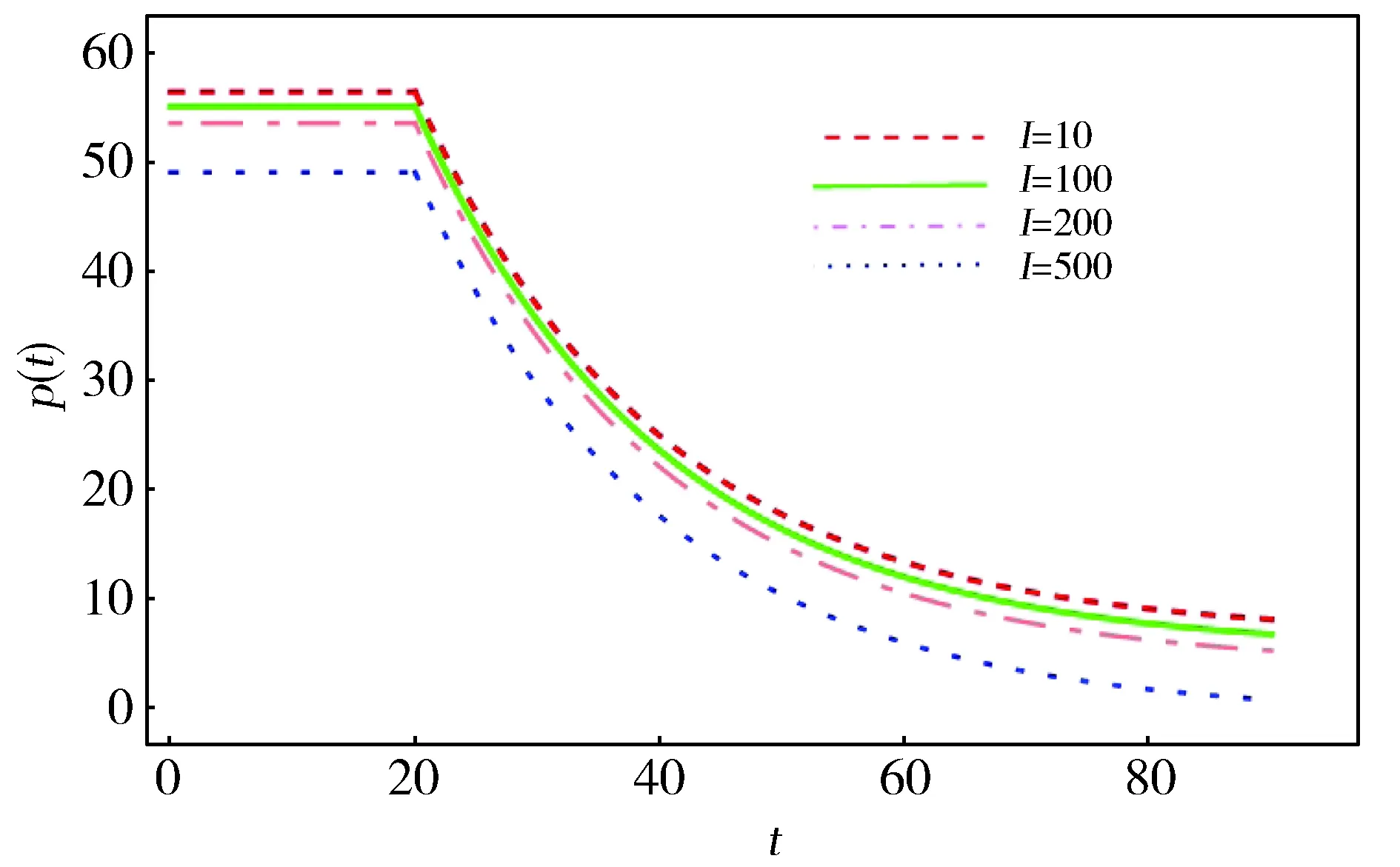
Fig.3 Optimal pricing changes with different inventory图3 最优定价随库存变化图

Fig.4 Optimal pricing changes with different sales cycle图4 最优定价随销售周期变化图

图4是零售商定价策略随销售周期变化图。从图中可以看出,随着销售周期的延长,整个周期的价格呈现整体下降趋势,这是因为零售商有了更大的定价空间。当销售周期较短,且满足I≥λT/2时,即使销售周期改变,第一阶段的定价策略完全一致,第二阶段定价也相同,只是销售时间不同。

3 结论

针对产品价值判断异性且购买产品时采取模糊决策的消费者,本文研究了非即时衰减品的最优定价问题。考虑到销售量存在的约束,建立了以零售商总利润最大化为目标的最优控制模型,并运用变分法求得产品的最优动态定价策略。结果表明:由于产品的非即时衰减特性,零售商会采取两阶段的定价模式,其中第一阶段是静态定价,第二阶段采取动态定价策略;由于产品价值的衰减,价格函数为递减函数,与实际情况相符;随着衰减因子的增大或保鲜期的缩短,最优定价都会相应下降,这就要求零售商要加大保鲜投入延缓产品价值衰减速度。

为了使模型更贴近实际情况,本文考虑了产品价值非即时衰减特性对定价的影响,在之后的研究中还可以引入更多的实际因素,如:企业的保鲜努力水平[14]、消费者对产品的偏好[15-16]、品牌忠诚度对产品定价的影响[17-18]等,以及考虑供应商补货的多周期销售问题同样值得深入探讨。