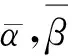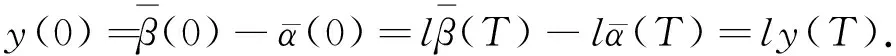一阶非瞬时脉冲微分方程边值问题

姚美萍,胡静

(山西大学 数学科学学院,山西 太原 030006)

近年来,脉冲微分方程理论已成为一个重要的研究领域[1-4]。非瞬时脉冲微分方程作为一类新型脉冲理论,自2013年由Hernndez和O’Regan在文献[5]中首次提出并给出相关理论后,文献[6-12]及其参考文献研究了非瞬时脉冲微分方程解的存在性理论。单调迭代技术结合上下解方法是研究微分方程解的存在性的一个重要工具,近年来一直被学者们所关注[13-17]。但将单调迭代技术应用到非瞬时脉冲微分方程解的存在研究相对较少[18-19]。本文考虑了一阶非瞬时脉冲微分方程边值问题。

(1)

其中,fk∈C((sk,tk+1]×R,R),k=0,1,…,p,φk∈C((tk,sk]×R×R,R),k=1,2,…,p,0=s00和T∈R.

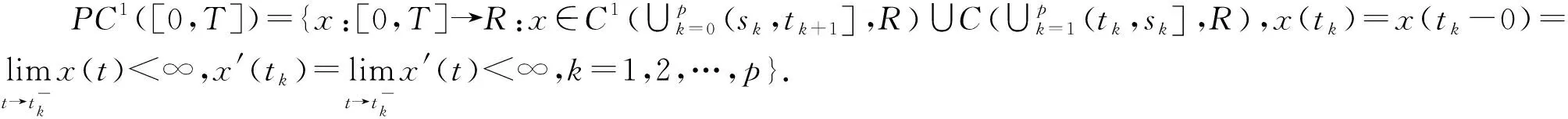
定义1 称α(t)是问题(1)的一个下解。若α∈PC1([0,T])且满足

若上述不等式反号,可定义问题(1)的一个上解。

考虑线性非瞬时脉冲微分方程边值问题

(2)

其中Mk∈R,l>0,σk∈C((sk,tk+1],R),k=0,1,…,p,Lk,Kk,φk∈C((tk,sk],R),k=1,2,…,p.

其中0≤s≤t≤T,i≤k,k=0,1,…,p+1和i=1,2,…,p+1.

由分析技巧,可得如下关于问题(2)解的存在唯一性结论。

引理1 当le-MpTG1,p(sp,0)≠1时,问题(2)存在唯一解。

证明首先由归纳法可知脉冲微分方程

(3)

在初始条件m(0)=m0下有唯一解m(t)如下

(4)

因此

结合边界条件m(0)=lm(T)以及le-MpTG1,p(sp,0)≠1,有

将m0代入(4),即可知问题(2)有唯一解存在。引理证毕。

注1 引理1证明中的表达式(4)给出了非瞬时脉冲微分方程初值问题解的统一表达式,而在已有非瞬时脉冲微分方程的相关文献中只是给出了解在每个小区间上的表达式,并且每个小区间上解的表达式依赖于解在前一个小区间上的值。

引理2 假设m∈PC1([0,T])且满足

其中Mk∈R,l>0,Kk∈C((tk,sk],(-∞,1)),Lk∈C((tk,sk],R+).若

le-MpTG1,p(sp,0)<1

(5)

则m(t)≤0,t∈[0,T].

证明令方程(3)中的σk(t)≤0,φk(t)≤0,则由(4)式可知方程(3)的解m(t)有如下估计

m(t)≤m(0)e-MktG1,k(sk,0).

(6)

结合m(0)≤lm(T),有

由条件(5)可知m(0)≤0.进一步由(6)可得m(t)≤0,t∈[0,T].引理证毕。

方便起见,列出以下所需条件。

(H1) 函数α,β∈PC1([0,T])分别是问题(1)的下解和上解且α(t)≤β(t),t∈[0,T].

(H2) 对k=0,1,…,p,函数fk∈C((sk,tk+1]×R,R)且存在常数Mk>0使得

fk(t,x)-fk(t,y)≤-Mk(x-y),

α(t)≤x≤y≤β(t),t∈(sk,tk+1],k=0,1,…,p.

(H3) 对k=1,2,…,p,函数φk∈C((tk,sk]×R×R,R)且存在Kk∈C((tk,sk],(-∞,1)),Lk∈C((tk,sk],R+)使得

φk(t,x1,y1)-φk(t,x2,y2)≤Lk(t)(x1-x2)+Kk(t)(y1-y2),

α(tk-0)≤x1≤x2≤β(tk-0),α(t)≤y1≤y2≤β(t),t∈(tk,sk],k=1,2,…,p.

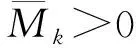
α(t)≤x≤y≤β(t),t∈(sk,tk+1],k=0,1,…,p.

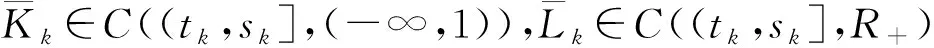
α(tk-0)≤x1≤x2≤β(tk-0),α(t)≤y1≤y2≤β(t),t∈(tk,sk],k=1,2,…,p.

定理1 假设(H1)-(H3)和(5)成立,则存在单调迭代序列{αn(t)},{βn(t)}在[α,β]分别一致收敛于问题(1)的极小解和极大解。

证明对任何函数η∈PC1([0,T]),我们考虑问题(2),其中

由引理1可知问题(2)有一个唯一解m存在。

定义算子Φ:PC1([0,T])→PC1([0,T])为Φη=m.则Φ有下面的性质。

(i)α≤Φα和Φβ≤β.

(ii)Φ在[α,β]是不递减的。即若η1≤η2,η1,η2∈[α,β],则Φη1≤Φη2.

首先证明(i),设α1=Φα,y=α-α1.则

-Mky(t),t∈(sk,tk+1],k=0,1,…,p,

y(t)=α(t)-α1(t)≤φk(t,α(t),α(tk-0))-Lk(t)α1(tk-0)-

Kk(t)α1(t)+Lk(t)α(tk-0)+Kk(t)α(t)-φk(t,α(t),α(tk-0))≤

Lk(t)y(tk-0)+Kk(t)y(t),t∈(tk,sk],k=1,2,…,p,

y(0)=α(0)-α1(0)≤lα(T)-lα1(T)=ly(T).

由引理2,我们有y(t)≤0,t∈[0,T],从而α(t)≤(Φα)(t),t∈[0,T]. 因此,α≤Φα. 类似地可以得到Φβ≤β.

其次证明(ii).令u1=Φη1,u2=Φη2和y=u1-u2,结合(H2),(H3).我们有

-Mky(t),t∈(sk,tk+1],k=0,1,…,p,

y(t)=u1(t)-u2(t)=Lk(t)[u1(tk-0)-η1(tk-0)]+

Kk(t)[u1(t)-η1(t)]+φk(t,η1(t),η1(tk-0))-

Lk(t)[u2(tk-0)-η2(tk-0)]-Kk(t)[u2(t)-η2(t)]-φk(t,η2(t),η2(tk-0))≤

Lk(t)y(tk-0)+Kk(t)y(t),t∈(tk,sk],k=1,2,…,p,

y(0)=u1(0)-u2(0)=lu1(T)-lu2(T)=ly(T).

由引理2,我们有y(t)≤0,t∈[0,T]. 因此,Φη1≤Φη2.

定义函数序列{αn(t)},{βn(t)}为Φαn=αn+1,Φβn=βn+1,n=0,1,…,其中α0=α,β0=β. 由性质(i)和(ii),我们可以得到

α0≤α1≤…≤αn≤…≤βn≤…≤β1≤β0.

假设对某个n,有αn≤x≤βn. 令y=αn+1-x,则我们可得

y′(t)=-Mk[αn+1(t)-αn(t)]+fk(t,αn(t))-fk(t,x(t))≤

-Mky(t),t∈(sk,tk+1],k=0,1,…,p,

y(t)=Lk(t)[αn+1(tk-0)-αn(tk-0)]+Kk(t)[αn+1(t)-αn(t)]+

φk(t,αn(t),αn(tk-0))-φk(t,x(t),x(tk-0))≤

Lk(t)y(tk-0)+Kk(t)y(t),t∈(tk,sk],k=1,2,…,p,

y(0)=αn+1(0)-x(0)=lαn+1(T)-lx(T)=ly(T).