高斯态的量子相干度量

王洋洋,齐霄霏

(山西大学 数学科学学院,山西 太原 030006)

0 引言

(C1)C(ρ)≥0;C(ρ)=0当且仅当ρ∈I;

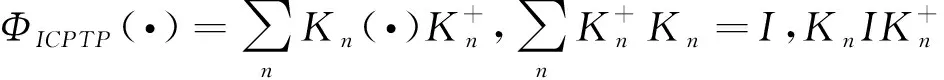
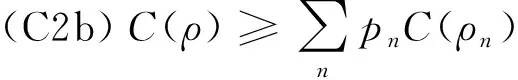
文献[4]也给出了一些相干度量,例如由l1-范数、相对熵、迹范数、保真度等诱导的相干度量。随后许多学者开始进行量子相干各个方面的研究,详见文献[5-10]。近来,文献[11]把相干度量理论推广到了无限维上。

高斯态是无限维系统中连续变量系统上一类重要的量子态。对任意n-模量子态ρ,其特性函数χ(z)定义为:

χ(z)=Τr(ρW(z)),z∈R2n

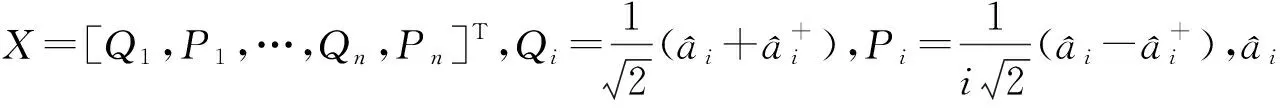
进一步,如果ρ的特性函数χ(z)可以写成如下形式:

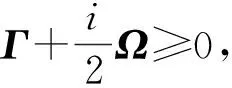
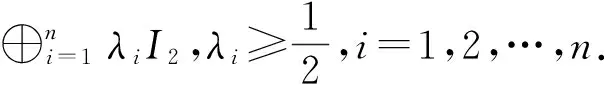
文献[14]利用Uhlmann保真度刻画了高斯态的量子相干性。对任意单模高斯态ρ,其量子相干性CBu(ρ)定义为:

(1)

本文的目的是试图给出CBu的一个上、下界,从而获得量CBu的一些性质特征。

1 主要结果

设H是任意维Hilbert空间。对任意量子态ρ,σ∈S(H),其sub-保真度E与super-保真度G分别定义为:

(2)

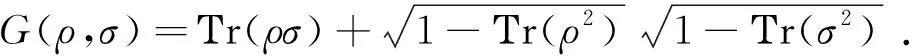
(3)

易证E与G有很好的性质,譬如:

(i) 对称性:E(ρ,σ)=E(σ,ρ),G(ρ,σ)=G(σ,ρ);

(ii) 有界性:0≤E(ρ,σ)≤1,0≤G(ρ,σ)≤1 并且G(ρ,σ)=1当且仅当ρ=σ;

(iii) 酉不变性:E(ρ,σ)=E(UρU+,UσU+),G(ρ,σ)=G(UρU+,UσU+)对任意酉算子U成立；

(iv)E(ρ,σ)≤F(ρ,σ)≤G(ρ,σ).

关于二者更多性质,参见文献[15-17]及里面的参考文献。

现在,利用E与G我们可以定义两个新的相干度量。

定义1 令H是任意维复Hilbert空间.对任意量子态ρ∈S(H),定义如下两个量:

其中I表示非相干态全体。

利用定义1、等式(1)与性质(i)-(iv),显然有CE(ρ)≥CBu(ρ)≥CG(ρ); 0≤CE(ρ)≤1,0≤CG(ρ)≤1;CG(ρ)=0蕴含ρ为非相干态。

下面我们将限制在高斯态上讨论CE与CG的性质,进而获得CBu的结构性质。

首先给出CE与CG的计算公式。

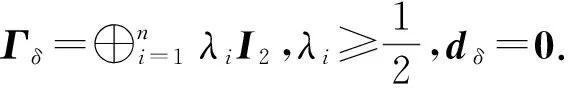
其中Γρ,Γσ与dρ,dσ分别为ρ与σ的相关矩阵与均值向量,Δd=dρ-dσ.则由上式可得

(4)

与

(5)

此外,由文献[16]有

(6)

综合等式 (2)-(6),即得

CE(ρ)=1-

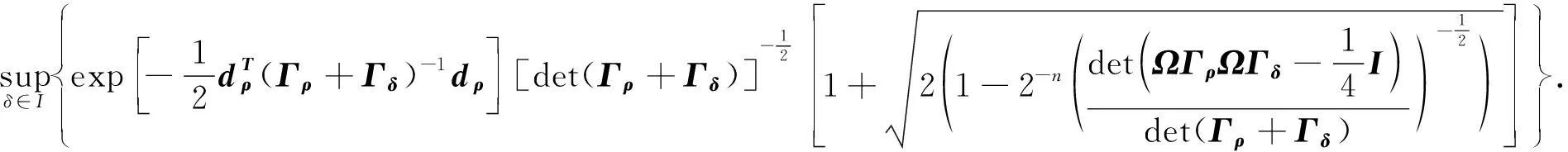
(7)

和

(8)

对于高斯纯态,我们有下面的命题成立。

命题1 对任意n模高斯纯态|Ψ〉〈Ψ|,我们有

CE(|Ψ〉〈Ψ|)=CBu(|Ψ〉〈Ψ|)=CG(|Ψ〉〈Ψ|).

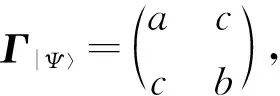
证明对任意n模高斯纯态|Ψ〉〈Ψ|,由定义得

CE(|Ψ〉〈Ψ|)≥CBu(|Ψ〉〈Ψ|)≥CG(|Ψ〉〈Ψ|),故

CE(|Ψ〉〈Ψ|)=CBu(|Ψ〉〈Ψ|)=CG(|Ψ〉〈Ψ|).

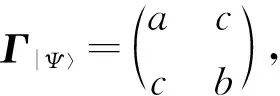
对于任意单模高斯态,我们有:

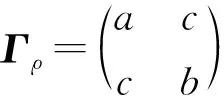
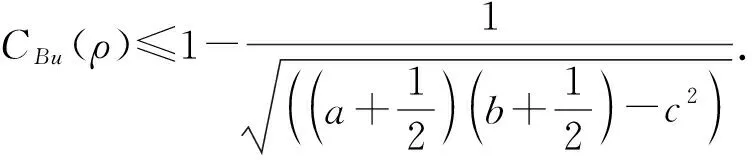
(9)

由于Γρ是实正定矩阵,因此存在正交矩阵U与正数x1,x2使得Γρ=Udiag(x1,x2)UT其中diag(x1,x2)表示对角线元素为x1,x2,其他元素为零的2阶矩阵。再记Udρ=(d1,d2)T. 因此等式(9)可化为

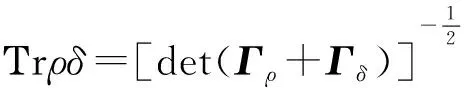
证毕。

最后,给出相关矩阵是标准形式的双模高斯态的CBu的上下界。

假设ρ是任意双模高斯态,若其相关矩阵具有如下形式:

(10)

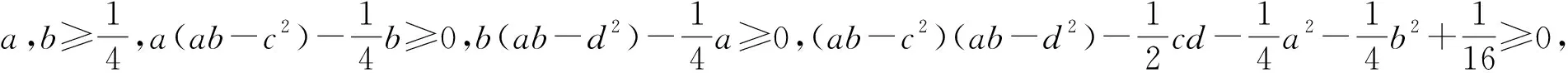
命题3 假设ρ是双模高斯态,其均值向量为0且相关矩阵Γρ具有形如等式(10)的标准形式。下列表述成立:

(ii) 若ρ是非纯态,则下列不等式成立:

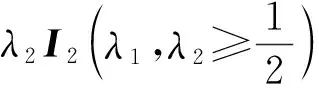
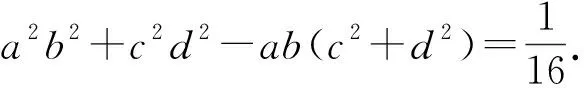
容易验证

若ρ是非纯态,因dρ=0,再次利用等式(7),得到

另一方面,由等式(2)即有

证毕。