火箭弹电动舵机模糊单神经元PID控制算法

孙建飞，辛长范

（中北大学机电工程学院，太原030051）

随着高新技术的发展和为满足现代战争局部化的需求，精确打击能力和控制智能化正在引入制导弹药导航与控制中。现代智能火箭弹制导系统的主要控制形式是：采用精确导引和智能控制技术，在弹的飞行过程中能够实时测量弹与理想弹道的误差，并通过弹上的控制执行机构及时修正实际弹道，最终达到精确打击目标的目的[1]。舵机系统是火箭弹飞行控制的执行机构，控制弹的飞行很大程度上就落实到舵机的控制上。因此，舵片的位置能否在其控制系统下快速准确响应和超调是否较小，这成为制导弹药能否精确制导的重要指标[2]。

对于智能火箭弹，其飞行环境复杂多变，使得弹箭舵机伺服系统动静态特性实时变动。如果火箭弹在常规PID 控制下，其控制参数在几乎整个控制飞行进行中变化缓慢，这样会造成精度低和抗干扰性较差等缺点[3]。随着计算机技术的发展，出现了专家PID控制器，这种控制器必须精确地确定对象模型和对长期实践经验的控制规则模型化，但是对于操作者经验不易精确描述，控制过程中各种信号量以及评价指标不易定量表示，专家PID 方法受到限制。模糊理论是解决这一问题的有效途径[4]，把规则条件和操作用模糊集表示，并把这些模糊控制规则以及有关信息作为知识存入计算机知识库中，然后计算机根据控制系统的实际响应情况，应用模糊推理即可实现自动对PID参数的最佳调整。模糊PID控制能够很好地适应被控对象非线性和环境时变性，具有较强的稳定性，因而其算法更加符合舵机的控制需求。

但是，模糊数学的建立有着对大量控制经验的要求[5]，并在输入、输出上难免受到其论域范围有限和模糊子集划分欠妥的影响，导致模糊控制的响应慢，超调量大。对于这些问题，需要对传统模糊PID 进行相应的改进，以更好地满足智能火箭弹对舵机控制高标准的要求。

根据上述分析，在此提出模糊单神经元PID控制，将模糊推理与单神经元算法融合之后，再利用PID 控制输出，以2种算法的优劣互补为思路，设计出一种能快速精确响应的智能PID 控制器，提高了舵机控制系统的控制精度、稳定性和抗干扰能力。

1 制导火箭弹舵机系统建模

1.1 舵机系统的工作原理

弹体在大气飞行的过程中，为达到弹最终控制在预定弹道下飞行的目的，一般需要修改弹体周围的空气动力，来改变弹的受力情况[6]。

可控火箭弹是通过舵片的偏转改变弹体所受到的导转力矩、升力和阻力，从而改变对自身的控制力[7]。在飞行控制阶段中，弹载计算机会接收并处理弹体的位置和姿态信息，最后输出所需的舵偏角指令，输出的舵偏角指令经过功率放大电路形成可驱动电机转动的电压，电机的转动通过齿轮组的减速最终作用在舵片上，舵片位置再通过传感器反馈给控制系统，最终完成对舵机的控制[8]。所以，对于舵偏指令，舵机系统需要作出快速和准确的响应，并且要做到超调量较小，才能使火箭弹能够稳定在理想弹道下飞行。

1.2 舵机系统的结构

可控火箭弹舵机系统主要组成有：控制器、信号功率放大器、直流伺服电机、减速器和舵偏角传感器。功率放大器是由脉宽调制器以及开关控制电路等部分组成；直流伺服电机分为有刷直流电动机和无刷直流电动机，一般在军工上采用无刷直流电机，减速器一般采用齿轮组合机构[9]。

1.3 舵机系统模型建立

1.3.1 无刷直流电机建模

电动机是舵机的核心动力执行元件，无刷直流电机主要由定子和转子组成，系统选用星型三相六状态无刷直流电机[10]。

三相无刷直流电机定子电压方程为：

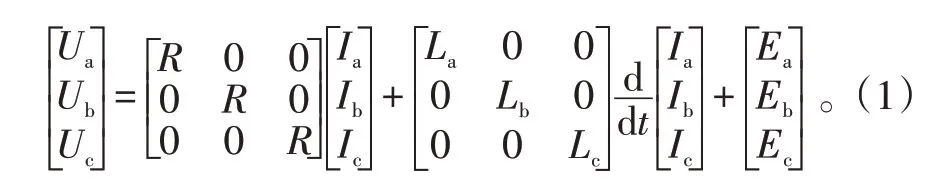
式（1）中：L为定子绕组电感；E表示绕组电动势；I表示绕组电流；U表示电压；t表示时间；R为电阻。

通过等效电路法将电机电路简化，可以得到简化后的电压方程为：

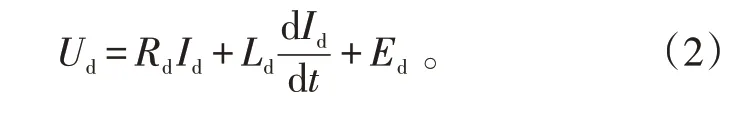
感应电动势方程为：

负载电机转矩方程为：

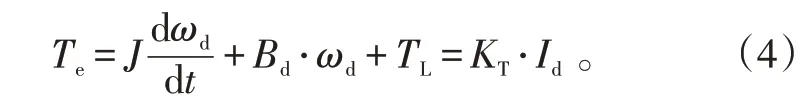
式（2）～（4）中：Ud表示电源电压；Rd表示回路总电阻；Id表示电枢电流；Ed表示感应电动势；Ld表示总电感；TL为电机负载转矩；ωd为电机机械角速度；Te为负载转矩；J为定子的转动惯量；KT为转矩系数；Bd为摩擦阻力因素[11]。

由此建立有负载转矩的无刷直流电机模型，其系统结构如图1所示，图中θd为电机输出转角。

图1 有负载转矩的无刷直流电机系统结构Fig.1 Brushless DC motor system structure with load torque

1.3.2 舵面动力模型建立

由舵片旋转产生的力矩为铰链力矩，即流过舵面的气流对舵轴形成的空气动力矩[12]，计算公式为：

式（5）中：TH为铰链力矩；ρ为空气密度；v为弹的空速；St为舵面面积；bt为舵面压心与弹轴距离；mh为铰链力矩系数导数；θt为舵偏角。

舵片偏转角为：

舵偏角传感器的角度转化式为：

式（7）中：uf为传感器信号；N为减速器传动比；Kf传感器角度转换比[13]。

1.3.3 舵机系统整体模型

根据舵机系统的组成和功能，将电机系统设计为电流环、转速环和位置环三闭环系统模型，最终舵机系统建立的模型如图2 所示。电流环和转速环为内环，模拟实时的电机电流和转速；外环为位置环，响应舵偏指令yd，精准控制舵机位置[14]。

图2 电动舵机系统Fig.2 Electric steering gear system

2 模糊单神经元PID控制器

2.1 智能控制器整体设定

此智能PID 控制器位于位置控制环，控制器结构主要是：以模糊PID控制为主框架，引入结构较为简单的单神经元在线修改部分参数；然后，将输出的比例系数kp、积分系数ki和微分系数kd传送到PID控制器中；最终，由PID 的输出控制目标对象，其结构原理如图3所示。

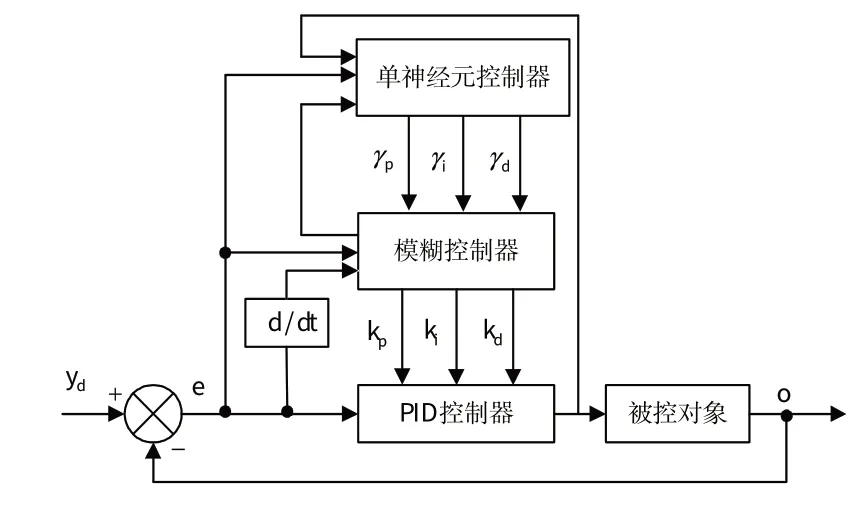
图3 模糊单神经元PID控制器Fig.3 Fuzzy single neuron PID controller

2.2 智能控制算法

2.2.1 输入变量模糊化

首先，根据模糊控制器输入变量的变化范围定义模糊集上的论域：

误差e和误差变化率δ的模糊子集为：

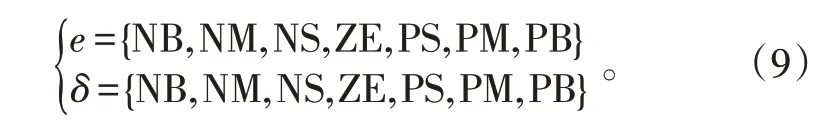
子集元素分别代表“负大”“负中”“负小”“零”“正小”“正中”和“正大”[15]。

输入模糊化就是对输入尺度变换，使变量适应在设定的论域中，设误差e和误差变化率δ的变换系数为γe、γδ，则模糊化后的值分别为γee和γδδ。比例系数调节量Δkp、积分系数调节量Δki和微分系数调节量Δkd的模糊子集均服从正态分布，e、δ的隶属度函数图见图4，因而可得出模糊子集的隶属度[16]。Δkp、Δki、Δkd的论域分别设为[- 3,3] 、[- 1,1] 和[- 1,1] 。

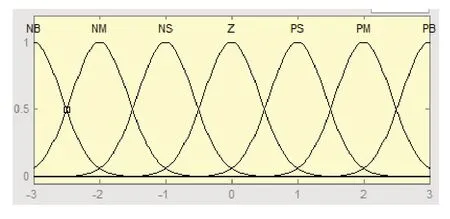
图4 e、δ 隶属度函数图Fig.4 Membership function graph of e and δ

2.2.2 模糊规则设置

模糊PID 控制以误差e和误差变化率δ作为输入，利用模糊控制规则在线对PID参数进行修改，以满足不同时刻的e和δ对PID参数自整定要求。

离散型PID控制算法为：

式（10）中：u(k)为PID输出；e(k)为误差；k为采样序号；T为采样时间。

再考虑kp、ki和kd的作用：

1）比例系数kp的作用是加快系统响应速度，提高系统调节精度。

2）积分系数ki可消除系统稳态误差。

3）微分系数kd可改善系统的动态特性，抑制误差的扩大，对误差变化作出预报，缩小控制量动态振荡。

制定规则：在电动舵机执行偏转命令开始阶段，增大比例系数取值，减小微分系数；在后期则相应地减小比例和微分系数的作用，扩大积分系数[17]。由此建立输入、输出的模糊规则表，见表1。

表1 模糊规则表Tab.1 Fuzzy rule list

由表1 和隶属函数可得出输出模糊子集的隶属度，再利用重心法进行反模糊化得到模糊控制器输出，计算式分别如下：

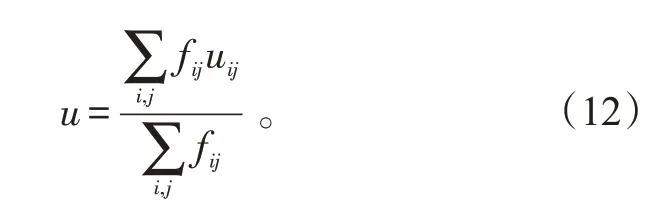
式（11）、（12）中：μi(e)、μ（jδ）分别为e、δ的隶属度；fij为输出参数的隶属度；u为模糊控制器输出；uij为所隶属模糊子集，其值由模糊规则表确定。

2.2.3 模糊输出参数

模糊控制输出参数为：

式（13）～（15）中：Δkp(0)、Δki(0)、Δkd(0)为PID 控制参数初值；γp(j)、γi(j)、γd(j)为模糊输出的修正参数的比例系数；γp(0)、γi(0)、γd(0)为比例系数的初值。

比例系数的确定直接影响着PID 控制性能，传统模糊PID的比例系数是根据经验所得[18]。

2.2.4 比例系数的单神经元自整定法

根据有监督Hebb 学习规则，设计有自学习能力的单神经元自适应系数调整器[19]，其结构如图5所示。

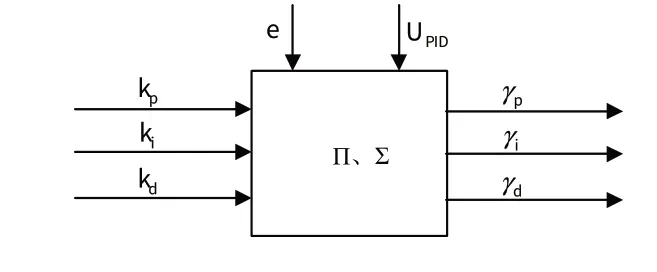
图5 单神经元结构图Fig.5 Structure diagram of single neuron

具体算法为：

式（16）～（18）中：ηp、ηi和ηd分别为比例、积分、微分的学习系数；UPID为PID控制器的输出。

3 仿真分析

通过Matlab-Simulink 工具建立火箭弹舵机控制系统仿真模型。选用的无刷直流电机参数：额定电压36 V，额定电流6.7 A，电枢回路总电阻0.78 Ω，电枢回路总电感1.25×10-3H，转矩系数0.097N ⋅m/A，反电动势系数7.3V/krpm，机械时间常数4.33×10-3s[20]，功率放大系数5，减速器传动比为210，γp、γi和γd初值分别为4、0.5 和0.25，学习系数ηp、ηi、ηd分别为0.4、0.015、0.1。

针对控制系统输入阶跃信号和正弦信号的响应和静动态特性来做仿真验证，模型中的电流环和速度环封装于舵机伺服系统中，系统仿真结构如图6所示，并得到仿真结果如图7～10所示。

在实验验证中，分别输入幅值为0.4、0.5、0.6的阶跃信号和振幅为1的正弦信号，并收集输出结果，观察对比2个控制器的控制性能，整理得出表2。

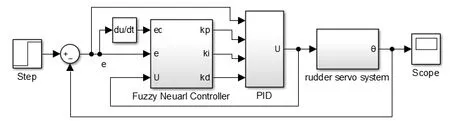
图6 系统仿真结构Fig.6 System simulation architecture

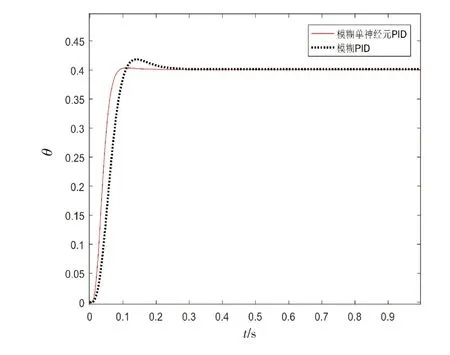
图7 幅值为0.4的阶跃响应Fig.7 Step response with amplitude of 0.4

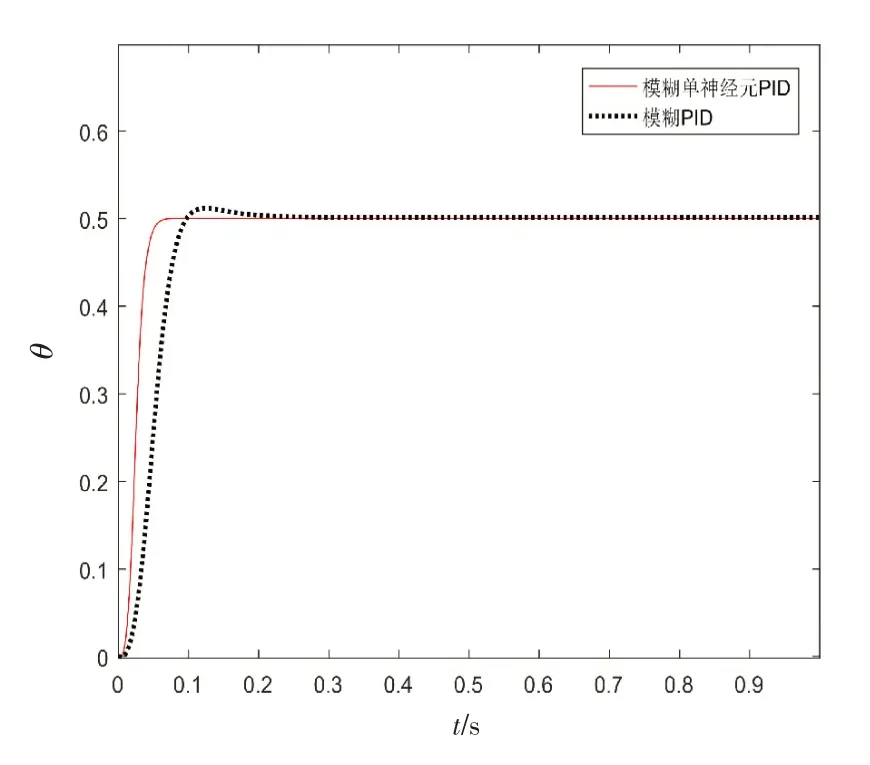
图8 幅值为0.5的阶跃响应Fig.8 Step response with amplitude of 0.5

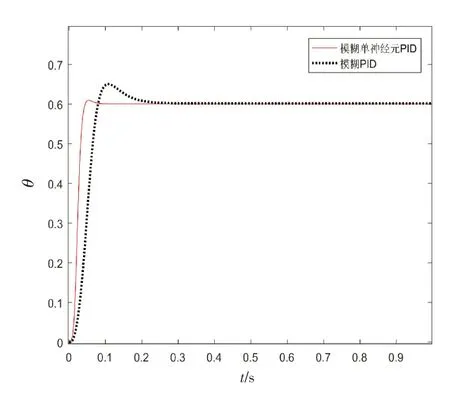
图9 幅值为0.6的阶跃响应Fig.9 Step response with amplitude of 0.6

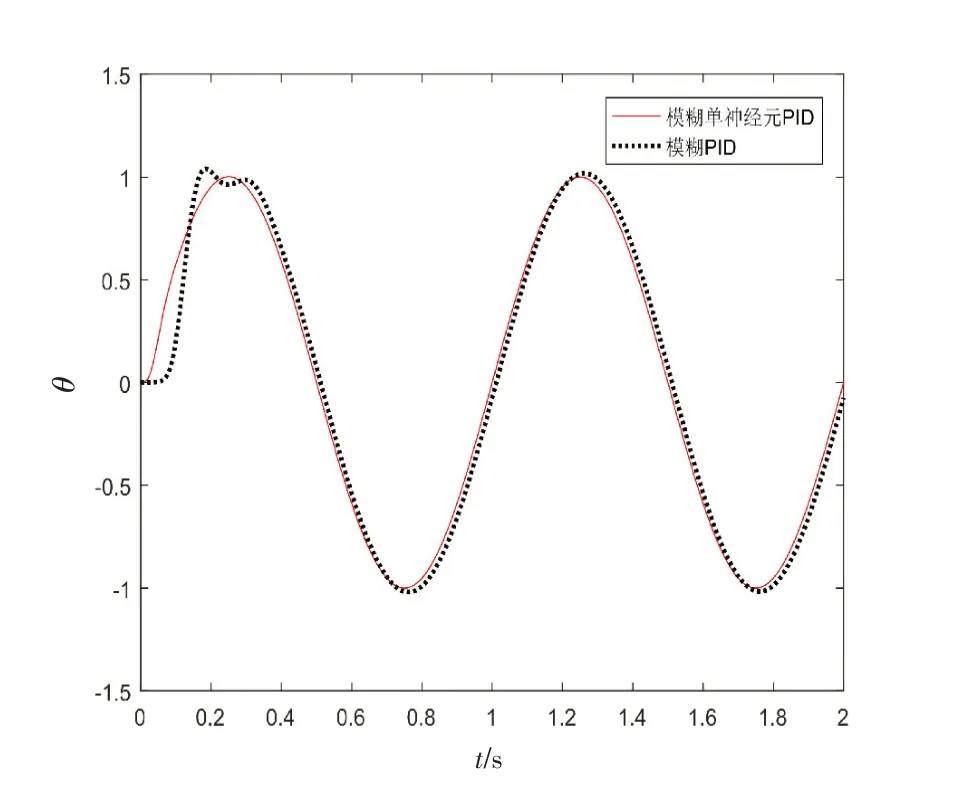
图10 振幅为1的正弦跟随Fig.10 Sinusoidal tracking of amplitude 1

表2 控制器的性能指标Tab.2 Performance indicators of the controller

综合上述结果和分析得出：模糊单神经元PID 相比传统模糊PID阶跃响应速度要快，超调量明显缩小，动态时间缩短0.1 s 左右；在正弦跟随方面减小了4 ms的跟随滞后，舵偏角的最大误差也明显减小。由此可见，模糊单神经元PID控制算法改进了传统模糊PID，能够快速、准确、稳定地控制、执行舵偏指令，符合火箭弹弹道修正对舵机控制的要求。

4 结束语

本文研究了火箭弹电动舵机的模糊单神经元PID控制算法。首先，对火箭弹舵机系统进行建模；再立足于模糊推理和Hebb学习规则设计了参数自整定的模糊单神经元PID控制算法；最后，经仿真验证，模糊单神经元PID 控制相比传统模糊PID 控制，其信号响应的动态特性和跟踪性能均得到改善，并且降低了模糊控制对经验积累的要求，在提高舵面控制的快速性和准确性的同时，使得控制器的设计得到简化。