利用神经网络的海杂波幅度分布参数估计方法

王国庆，王朝铺，刘传辉，刘宁波，丁 昊

（1.海军航空大学，山东烟台264001；2.北京理工大学计算机学院，北京100081）

对海探测雷达面临复杂的探测背景，其接收的回波信号中除了感兴趣的目标回波外，通常还包含海杂波等[1]。海杂波功率水平通常较高，伴有显著的非高斯、非平稳特性，易受各种复杂、多变因素的影响，已成为影响雷达探测性能的主要制约因素之一[1-2]。基于此，国内外学者提出了一系列模型进行海杂波特性认知，其中，幅度分布模型是较为重要的一种类型，其建模精度对统计类信号处理算法的设计与优化具有重要的理论和实践指导意义。瑞利模型是较早应用的统计模型之一，主要适用于中等或较高掠射角条件下低分辨率雷达海杂波的幅度分布建模。随着分辨率的提高，海杂波统计分布通常偏离瑞利模型，表现为尖峰和拖尾的增强，在小擦地角时更为明显[3]。为了提高理论模型与实测数据的吻合程度，一些双参数或三参数非高斯模型[4]，如对数正态、韦布尔、K、GK（GeneralizedK-distribution）等分布模型，在海杂波幅度分布建模中得到应用[5]。不同雷达参数及海洋环境参数条件下海杂波幅度分布特性存在较大差异，且不同模型在动态范围、拖尾程度上各异。因此，目前不存在一个通用的模型形式来概括已有的幅度分布模型[6-8]。

在模型形式给定的前提下，如何利用实测数据有效估计出模型参数是建模阶段须要解决的另一重要理论问题，且参数估计性能直接关乎模型的建模精度。目前，公开文献中主要采用的参数估计方法有最大似然估计方法、矩估计方法和数值优化方法，这些方法均以传统数理统计方法为理论基础，单次估计对样本的需求量大，不利于海杂波模型参数的在线实时估计，而且在多参数条件下，通过统计优化方法得到的估计结果容易陷入局部最优解，导致建模准确度下降。

为解决传统数理统计参数估计方法的非实时性和局限性问题，本文尝试将深度神经网络模型应用于海杂波幅度分布模型参数估计领域。近年来，深度学习理论在雷达领域得到了广泛的应用，它是一种高效的智能化信号处理方法，主要优势在于，通过组合低层特征形成更加抽象的高层表示属性类别或特征，以发现数据的分布式特征表示。通过低维的特征组合，可以形成不同的高维特征，最终形成不同的类别或高阶函数。相比起以往的浅层神经网络，深度学习具有更优的泛化能力、鲁棒性，以及更高的准确率，并且适用范围更广，实时性好。借助这种优势，深度学习理论在雷达目标分类识别方面比常规技术具有显著的性能改善[9-16]。然而，其在参数估计的应用方面尚属空白，实际上，对于特定的理论分布模型，参数估计问题可以抽象为复杂的非线性优化问题，而深度学习理论在解决该类问题上具有明显的技术优势。基于这种考虑，本文构建了具备高精度参数估计能力的深度神经网络模型，通过选取合理的深度神经网络结构并训练深度学习模型，使其通过自主学习的形式具备多参数估计能力，并利用仿真数据和X波段实测海杂波数据进行了性能验证。

本文给出的深度神经网络模型还可进一步扩展应用于海杂波的多普勒谱模型、空间相关模型等多参数模型参数估计领域，并有望取得更加优异的估计性能。

1 深度神经网络模型

神经网络是一种模拟动物神经网络行为特征，进行分布式并行信息处理的算法数学模型[17]。目前，多层前馈神经网络（Back Propagation，BP 神经网络）应用最为广泛，其网络的学习过程分为两部分，分别是信号的前向传导和误差的反向传播，即误差输出时按从输入到输出的方向进行，而调整权值时从输出到输入的方向进行反向更正。信号前向传导时，输入的信息通过输入层与权值作用，传播到隐含层；之后，同样与权值作用在此传播到输出层，计算期望输出与实际输出的误差；然后，进入误差反向传导的过程。误差反向传导，将最终误差通过隐含层反向传导至输入层，将总体误差分摊给各层的所有节点，进而调整各单元的权值，使误差沿梯度方向下降，经过反复学习与调整，得到误差最优值。一个4 层前馈神经网络如图1 所示，其包含输入层、两层隐含层和输出层，各层之间节点完全连接[18]。

图1 4层前馈神经网络Fig.1 Four-layer feedforward neural network

设神经网络的输入数据X格式为[x1,x2,…,xn] ，用Wki表示从前一层第k个节点到后一层第i个节点的权值，则各层之间的权值Wi表达式为：

为了在神经网络中加入非线性元素，采用ReLU（修正线性单元）作为激活函数，其表达式为：

于是得到第l层第i个单元的输出O(1)

i为：

单个样本的loss采用均方误差，其表达式为：

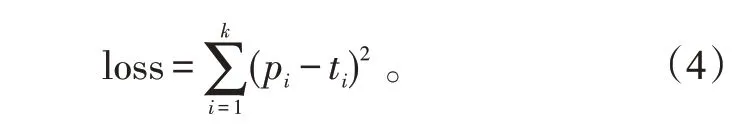
式（4）中：pi为样本预测值；ti为样本真实值；k为输出层神经元数。

2 基于深度神经网络的仿真海杂波数据多参数估计技术

采用全连接神经网络，将经过处理的海杂波数据（仿真数据）作为输入数据，经过多层全连接神经网络，获得海杂波模型影响参数；再将参数代入海杂波模型，作为代价函数反馈，进行反向传播，调整权重，重新输入海杂波数据训练计算，拟合程度越高，证明数据越符合该模型，直到获得较为理想的参数为止，并估算出海杂波模型的参数；最后，计算理论模型与经验拟合结果之间的误差。其流程图如图2所示。

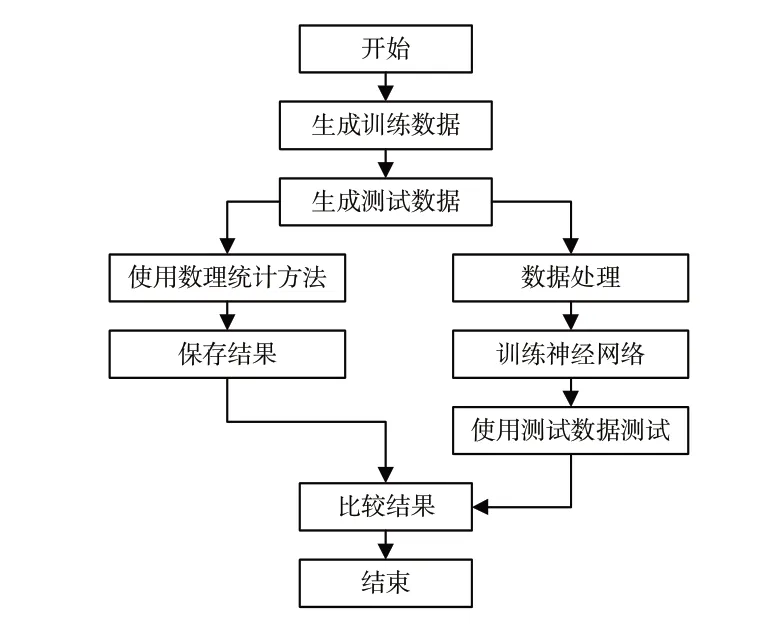
图2 模拟数据参数估计流程图Fig.2 Parameter estimation flow chart of the simulated data

1）构建数据集，生成参数指定的预训练数据，用于训练神经网络，并生成参数和格式同训练数据的预测试数据用于测试神经网络，用来比较神经网络和数理统计方法的估计结果差值。

2）对生成的预训练数据和预测试数据进行处理，采用直方图统计法，选取合适的区间大小和总体的数值范围，将处理之后的数据作为训练和测试的数据。

3）对所有预测试数据使用数理统计方法进行参数估计，估计每条数据的形状参数和尺度参数作为最终的比较结果之一，称为数理统计方法估计结果。

4）训练神经网络，输入经过处理的训练数据进行训练。一个网络训练一个参数，训练多个网络对应多个参数。得到与参数一一对应训练好的网络模型。

5）对训练好的网络模型进行测试，输入测试数据，得到神经网络估计结果，与数理统计方法估计结果进行比较，采用每个样本标签的平均偏差进行评估，偏差公式为：

式（5）中：n为数据的总数；Li为估计结果；Li,label为实际标签（为产生数据时的参数）。

3 基于深度神经网络的真实海杂波数据多参数估计技术

因为真实的海杂波数据不存在真实的标签，无法进行有监督学习，本文提出了使用仿真数据进行训练神经网络模型，使用真实的海杂波数据进行测试的方法。其操作流程图如图3所示。

图3 真实海杂波数据参数估计技术流程图Fig.3 Parameter estimation flow chart of the real sea clutter data

1）选取一种合适的数理统计估计的方法，对真实海杂波数据进行估计，得到数理统计方法估计结果。

2）选取测试参数，去除数理统计估计方法得到的参数中过大或者过小的结果，选取一个数据的分布参数范围，使该范围内存在较多的真实数据，并以此范围作为测试范围。选取参数范围时要考虑训练时间等问题，不能选取参数范围过大。否则，会出现过多不同参数组合的训练数据，或者训练参数离散化后跨度过大，导致神经网络拟合效果下降。

3）将选取的参数范围离散化，划分成多个均匀分布的数值，并按照这些离散的数值生成对应的仿真预训练数据。该步骤须要注意的是，如果要估计多个参数，应使用多个参数不同数值的组合训练网络，以使网络拥有对1 个参数的估计不受其他参数影响的效果。

4）选取合适的数值范围和区间长度，对预训练数据（仿真数据）和真实数据使用直方图统计法进行处理。

5）使用训练数据（仿真数据）训练神经网络。训练完成后，对真实数据进行预测，得到神经网络对真实数据的估测结果，并计算其卡方检验值。将神经网络的结果卡方值同数理统计方法估计结果的卡方检验值进行比较，验证算法的优劣。

4 实验及结果分析

为了验证算法的有效性，分别采用产生的模拟海杂波数据和真实海杂波数据进行参数估计实验。实验使用TensorFlow 深度学习框架构建深层全连接神经网络，与典型的对数正态分布和K 分布进行比较。

对数正态分布、K 分布是较为常用的非高斯幅度分布模型。其中，对数正态分布模型的概率密度函数（Probability Density Function，PDF）为：

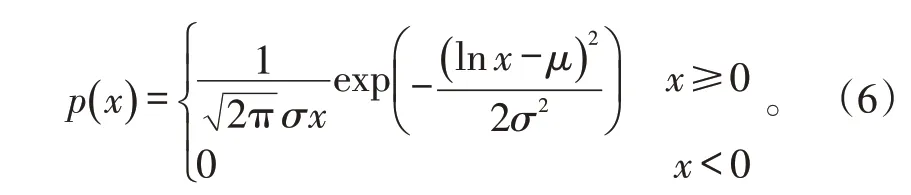
式（6）中：μ是尺度参数，表示分布的中位数；σ是形状参数，表示分布的倾斜程度。

模型的参数估计方法为：

K 分布模型的概率密度函数表达式为：

式（9）中：v为形状参数，表示海杂波的拖尾程度；b为尺度参数，与海杂波功率水平有关；Kv-1(⋅)为v-1 阶第二类修正Bessel函数。

K 分布的累积概率分布函数为：

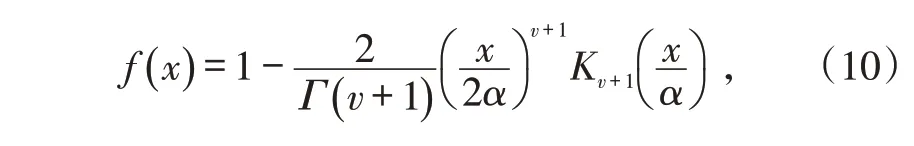
其n阶矩为：

由于K 分布不是初等函数，ML（Maximum Likehood）方法很难处理。对K 分布参数估计已提出多种方法。本文主要采用基于二阶和四阶矩的矩估计方法。

对于K 分布的矩，可以得到比值

是一个只与形状参数有关的量，由此方程就可得到v的估计，再代入任何一个矩中就得到α的估计。基于二阶和四阶矩的方法，取m=2 可得到求v的解析式：

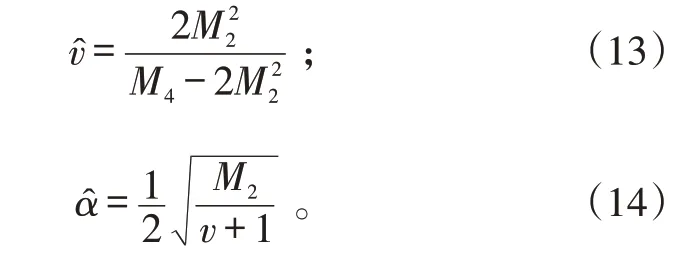
这种方法不需要数值求解，计算简单，是最常用的方法。但由于使用了较高阶的矩，对数据要求较高，如要求杂噪比高、样本数多等。

4.1 数据预处理

雷达数据的原始格式为数值形式，其单个位置的数据与最终估计的参数结果基本没有关联，且原始数据中包含低质量的样本（如对数正态分布数据中的小概率样本），训练神经网络直接对原始数据集的拟合效果不理想。为了提高参数估计的准确度，本文采用直方图统计的方法处理数据，按照原始数据的数值范围将之划分到处理后数据新位置。其总体思想是：一条符合某种概率分布的数据有多维，每一维的数值大小集中分布在一个范围内，且分布在这个范围内的数据基本决定这个数据的分布类型和参数，是适合用于训练神经网络的有效数值，如图4所示，服从这一参数的数据呈现对数正态分布，每一维数值集中在0～5 范围之内，只有个别维度数值大于5。故如果将原始数据处理为图中的柱状形式，这样的数据形式，每一个位置的数据都直接与最终的估计参数相联系，原始数据的概率分布没有改变，但增加了数据的价值密度，并且易于神经网络的训练。

概率也可用某一数值范围内数据出现的频数表示。为了筛选适合用于训练神经网络的有效数据，并更好体现该数据样本的数值分布特点，故将数据样本中的数值分布用柱状图表示。处理方法为：首先，选取一个合适的长度数值范围，保证此范围内包含大部分数据，在图4中，可以选取0～5的范围；然后，选取一个合适的区间长度，将预设数值范围按该长度划分为多个区间。单个区间长度不宜过大，这样会导致大量数据分布在同一个分组中，使模型精度下降。区间长度也不宜过小，过小会导致有的区间不存在数据，导致神经网络对该模型的拟合效果变差。所以应选择一个折中精度和准度的区间大小，将选取的范围划分为许多长度相同的区间，作为分割标准，按照图4，可以选取0.01作为区间长度。最后，将真实数据按照数值大小划分到各个区间中，每个分组上的数字表示在此分组数值范围内的数据个数，如一个数据包含1 000维，其中在0～0.01范围中有2维，则处理后数据的第0个位置的大小为2。同理，如在0.01～0.02 范围中有5维，则处理后数据第1个位置为5，以此类推。将处理后的数据作为最终的训练数据（输入）。处理方法如图5所示。

图4 对数正态分布柱形图与分布曲线Fig.4 Log-normal distribution histogram and distribution curve

图5 直方图统计法Fig.5 Histogram statistics method

这里以对数正态分布为例，不使用直方图统计法直接将原始数据放入神经网络进行训练，得到的测试结果如图6 a）所示；将原始数据使用直方图统计法处理之后再进行训练，得到的测试结果如图6 b）所示。

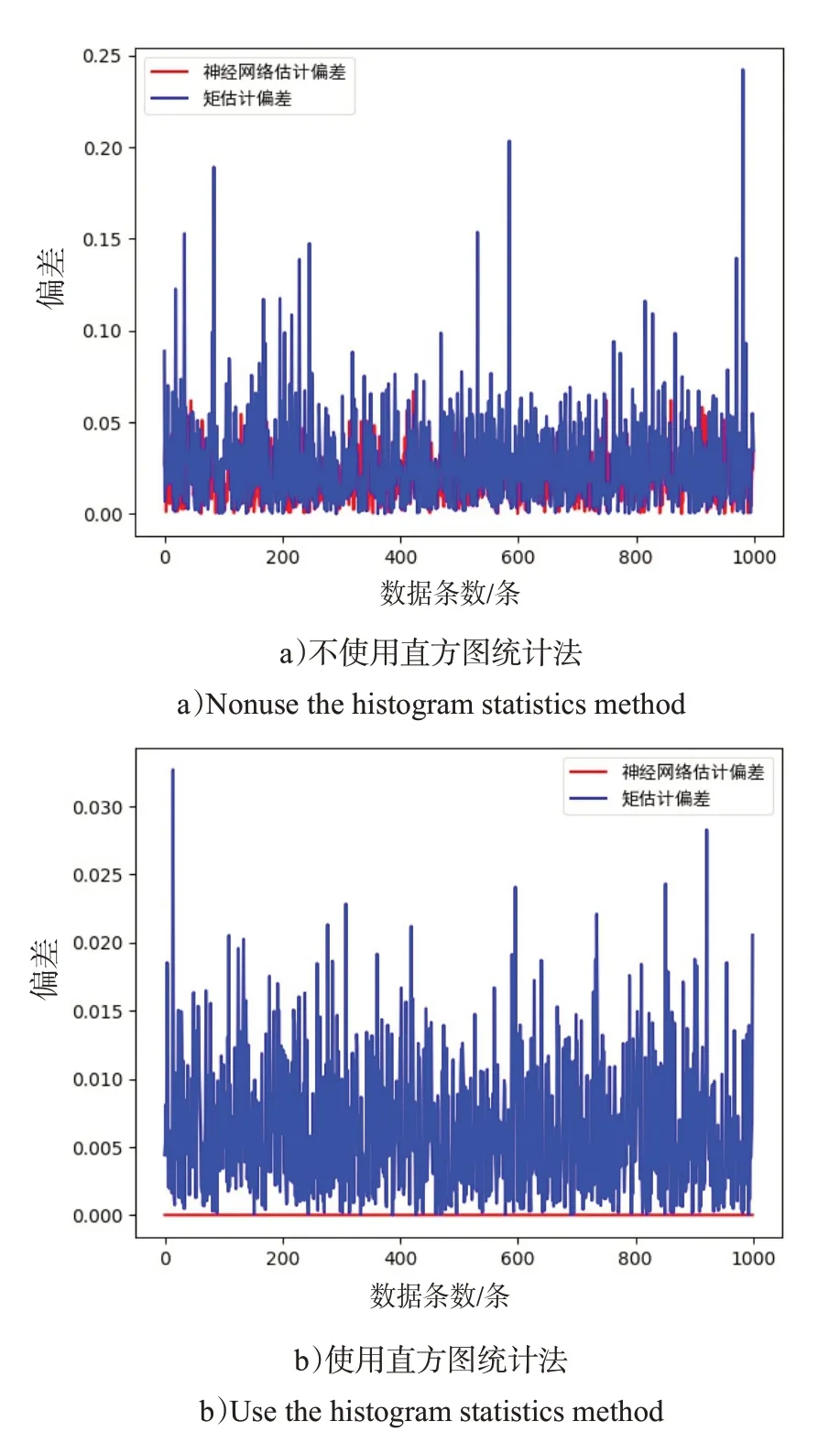
图6 参数估计的偏差比较Fig.6 Deviation comparison of parameter estimation

可以看出，使用没有经过直方图统计法的数据进行训练测试的神经网络对分布的拟合能力较弱，基本与矩估计方法持平。使用直方图统计法后的数据进行训练测试的神经网络对分布的拟合能力较强，在置信度超过98%的情况下优于矩估计方法。

4.2 仿真海杂波数据参数估计结果与分析

分别以对数正态分布和K 分布为例，在不同参数条件下产生仿真数据，通过训练对应的全连接神经网络进行参数估计，并与已有参数估计方法进行性能对比分析。所使用的神经网络为2 个4 层深度网络，其输入层均为1 000 个神经元，2 层隐藏层均各1 000 个神经元，输出层均1个神经元。针对每个参数，分别训练其对应的神经网络。神经网络结构如图7所示。

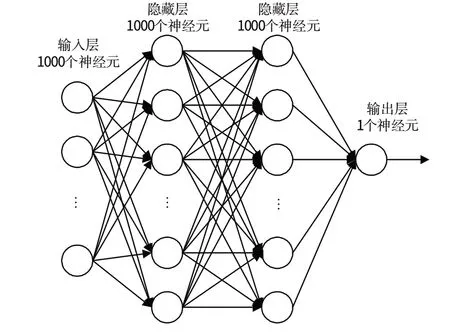
图7 神经网络形状Fig.7 Neural networks shape

4.2.1 对数正态分布参数估计结果分析

假定对数正态分布的尺度参数为-0.1，并在仿真时固定不变，形状参数分别为0.1、0.6、1.1 和1.6。在不同参数组合条件下各产生2 000 组仿真数据，每组2 048 维，每次训练50 条数据，共训练100 000 次。采用直方图统计法将2 048 维原始数据处理为512维，处理范围为0～5.12。测试数据400 组，每种参数100组，2 048 维，使用直方图统计法处理为512 维。采用相对偏差对参数估计精度进行定量度量，并与最大似然估计方法进行对比，得到的结果见表1。神经网络估计优于最大似然估计的置信度统计结果如表2 所示。通过对比可以看出，相比于传统的最大似然估计方法，基于神经网络估计方法的精度明显改善，且神经网络估计优于最大似然估计置信度可达97%以上。

4.2.2 K 分布参数估计结果分析

进一步以K 分布为例进行分析，假定尺度参数为1.0，形状参数分别为0.5、1.0、1.5和2.0，产生仿真数据的方法同上。与神经网络参数估计方法进行对比的已有参数估计方法为二阶/四阶矩方法，在表3、4 中，分别给出了相对偏差和置信度的对比结果，可以看出，对于K 分布，采用神经网络方法得到的参数估计结果明显在精度上优于传统的二阶/四阶矩估计。

表1 对数正态分布参数估计偏差对比Tab.1 Parameter estimation deviations comparison of log-normal distribution

表2 神经网络估计优于最大似然估计置信度Tab.2 Neural network estimation better than maximum likelihood estimation confidence

表3 K 分布参数估计偏差对比Tab.3 K-distribution parameter estimation deviation comparison

表4 神经网络估计优于二阶四阶矩估计置信度Tab.4 Neural network estimation better than second-order fourth-order moment estimation confidence

4.3 真实海杂波数据参数估计结果与分析

实验采用1993 年的IPIX 雷达数据进行参数估计。IPIX 雷达数据为131 072 维，单条数据分段符合某一概率分布，故对数据进行拆分。

经过测试，选择2 000 作为分组长度，选取数据分布参数集中的范围，设定K 分布形状参数为0.3～0.7，尺度参数为0.8～1.3，作为数据产生和训练范围。按照此范围共生成30种参数组合的训练数据，31 200 条数据，每条2 000 维。然后通过直方图统计法，选取数值范围0～4，区间长度0.01，得到溢出0～4 数值范围的数据为0.3%。使用4层的全连接神经网络进行训练，其形状同图7所示的网络，但输入层为400个神经元。

对比其结果与矩估计结果的优劣，使用卡方检验值作为评价标准，对包括神经网络方法在内的3 种方法进行比较，直观的结果如图8所示。

可以直接观察到，神经网络估计对真实分布的拟合情况优于K 分布的二阶四阶矩估计和对数正态分布估计得到结果。

对选取的97条测试数据进行卡方检验，对比对数正态分布矩估计和K 分布的二阶四阶矩估计，神经网络优于对数正态矩估计84 条，置信度87.5%，神经网络优于K 分布矩估计74 条，神经网络以76.29%的置信度优于矩估计。66 条数据神经网络估计优于K 分布矩估计5%以上，置信度68.75%。其结果如图9所示。

图8 IPIX雷达数据3种估计方法结果比较Fig.8 Comparison of three estimation methods based on the measured data of the IPIX radar

图9 数理统计与神经网络方法参数估计的卡方检验值比较Fig.9 Comparison of Chi-square test values between mathematical statistics and neural network method on parameter estimation

5 结论

本文针对传统方法进行的海杂波参数估计的问题（陷入局部最优解、缺乏实时性等），提出了一种基于深度神经网络的参数估计方法。针对神经网络对概率分布的原始数据拟合较差的问题，采用直方图统计法，降低了数据维度，增强了数据关联，增加了数据的价值密度。为了解决真实海杂波数据没有准确标签的问题，本文提出了采用仿真数据代替真实数据训练神经网络的办法。分别对仿真数据和真实数据进行了测试，对于仿真数据，本文方法优于传统估计方法（如最大似然估计和矩估计），置信度可达95%以上，对于IPIX 雷达实测海杂波数据，在置信度为76%的情况下优于传统的数理统计方法。