基于量测一致性的分布式多传感器多目标跟踪算法

邓 露，崔世麒

（1.92074部队，浙江宁波315000；2.海军航空大学，山东烟台264001）

多目标跟踪过程中，数据互联是将量测与目标航迹正确配对，以便后续滤波过程中能利用正确量测更新对应目标的估计值，避免因量测的错误互联导致目标状态估计精度下降。经典的多目标数据互联方法包括最近邻域算法、概率最近邻域算法、概率数据互联算法、联合概率数据互联算法、综合概率数据互联算法、多假设跟踪算法、最优贝叶斯算法等。其中，最近邻域算法和概率最近邻域算法的计算过程相对简单，计算量小，其他算法的计算过程相对复杂，计算耗时很大。但是前2种方法的跟踪精度相对其他算法有所下降，尤其是在高杂波密度和密集目标情况下，算法性能的区别比较明显[1-2]。

Kuo Chu C 等[3]将集中式结构下的JPDA 方法扩展到了分布式无线传感器网络（Wireless Sensor Network，WSN）中，并实现了多目标跟踪。以SCKF[4]的信息形式为基础，文献[5]提出了一种平方根容积信息一致性滤波器，通过JPDA 和信息量的适当加权降低虚假量测对跟踪的影响。文献[6]针对JPDA不能直接用于多传感器对多目标的跟踪，以极大似然估计完成了对来自多传感器的测量集合进行同源最优分划。文献[7]针对单传感器跟踪系统的缺陷，解决了多传感器多目标跟踪的数据关联问题。文献[8]将PF应用到传感器网络中，使得跟踪系统能解决非线性非高斯模型下的问题，并采用JPDA 的Monte Carlo实现完成数据互联。文献[9]将自适应分配算法和动态权值分配算法结合，以解决融合航迹误差低和不稳定性问题。文献[10]提出了基于高斯混合PHD 的多目标多传感器跟踪算法。文献[11]基于FISST 理论，构建一种反馈式多传感器PHD 融合跟踪框架。吴鑫辉等[12]以PHD滤波算法为基础，针对多传感器共同探测区域和盲区的情况，将PHD 推广到多传感器系统中，并提出了异步传感器丢失航迹的解决方案。Kamal A T推导出JPDA 的信息形式，并结合到信息一致性滤波算法中，解决了基于信息一致性的分布式WSN 跟踪多目标时的数据互联问题[13]。

上述算法都是用JPDA 或PHD 来完成数据互联，但这类算法计算复杂，所需的计算量大，且目标数量较多时容易出现数据组合爆炸。WSN 节点均为搭载有限设备和电源的小型传感器，需要完成信息获取、信息处理、通信等各项任务，因而传感器节点能分配给数据互联环节的计算负荷很少。考虑节约传感器资源并避免出现复杂数据组合，计算量最小的最近邻域算法更适合处理传感器网络中的数据互联问题[14]。

针对多目标分布式一致性跟踪问题，本文采用最近邻域关联方法实现网络中多传感器的数据互联，考虑最近邻域方法易受杂波影响从而误判杂波为量测的情况，对节点量测实施一致性迭代，进而提出基于量测一致性的分布式多传感器多目标跟踪算法（Distributed multi- sensor multi- target tracking algorithm based on measurement consistency，MC-DMMTA）。

1 问题描述

跟踪任务中，多个目标的运动状态一般是独立的。若跟踪场景中有t个目标，假设它们的状态方程为：

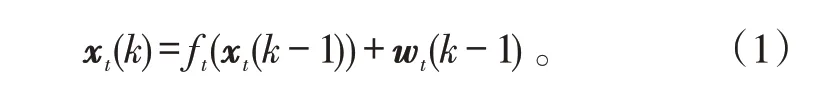
式（1）中：xt(k)表示k时刻目标t的状态；ft()是目标t的状态转移函数，在线性系统中用状态转移矩阵Ft来表示。假设所有目标的过程噪声符合零均值高斯分布，wt(k-1)～N(0,Qt(k-1))。

多传感器网络探测目标时，由于传感器观测性能的差异，其接收到的回波通常是不一样的，用z̑i(k)表示k时刻传感器i接收到的回波，其中包含多个目标的真实量测和杂波。每个目标的真实量测需要借助数据互联方法来判定。

如果一个WSN 由n个传感器构成，假设WSN 跟踪t个目标的量测方程为：

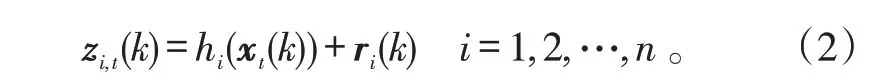
式（2）中：zi,t(k)表示k时刻传感器i对目标t的量测；hi()⋅是传感器i的量测转移函数，在线性系统中用量测转移矩阵Hi来表示。假设传感器i的量测噪声符合零均值高斯分布，ri(k)～N(0,Ri(k))。

2 基于量测一致性的分布式多传感器多目标跟踪算法

2.1 最近邻域算法确定量测

WSN跟踪多目标时，首先须要解决的问题依然是数据互联问题。解决数据互联问题旨在达到2 个目标：①在多个回波中找出真实量测（或是最接近真实量测的回波）；②确定量测与目标航迹之间的正确配对关系。

以下推导过程中，网络中各个传感器的运算是一样的，不妨用下标i来表示传感器i，i=1,2,…,n。

根据上一时刻的各个目标滤波结果或是已确定的各个目标最后一个航迹点预测本时刻状态：

式（3）～（5）中：x̂i,t(k-1)为上一时刻（k-1 时刻）传感器i中目标t的状态估计；x̂i,t(k|k-1)为本时刻（k时刻）传感器i中目标t的状态预测估计；Pi,t(k-1)为上时刻传感器i中目标t的状态协方差，Pi,t(k|k-1)为本时刻传感器i中目标t的状态预测协方差；zi,t(k|k-1)为本时刻传感器i中目标t的预测量测。

确定量测之前，由跟踪门初步筛选出部分回波成为候选回波，以限定下一步判定过程中的回波数量[15]。各个目标跟踪门的中心分别位于各被跟踪目标的预测位置zi,t(k|k-1)，跟踪门的大小由各自的新息协方差Si,t(k)来确定，需要确保有一定的概率接收到正确回波。

根据常用的椭圆（球）波门规则，当回波z̑i(k)满足下式时，认为该回波位于目标t跟踪门之内，于是将其选定为候选回波。式（7）中，γ由χ2分布表获得，会对真实量测落入椭圆（球）波门的概率产生影响，详情见文献[16]。

筛选所有回波，确定候选回波的集合之后，从候选回波中选取和波门中心统计距离最小的回波作为目标量测。

最近邻域法中的统计距离是新息加权范数：

根据式（8）计算各候选回波统计距离，各目标的候选回波分别比较后，便可确定目标t的量测zi,t(k)。

2.2 基于局部平均的量测一致性

最近邻域算法只需要计算出候选回波的统计距离，再比较大小确定目标量测，其简单的判断过程所花费的计算量也是相当小的。然而，简单的判断过程中能采取的判定依据是非常有限的。因此，判定出正确量测的概率较复杂判断过程会有所下降。对于最近邻域算法来说，最容易影响它判定正确量测的是数据互联中的杂波。当存在杂波（或其他目标的量测）离波门中心的统计距离小于真实量测离波门中心的统计距离，而且其被选定为候选回波时，最近邻域算法就会将该杂波确定为目标量测。错误量测会严重影响后续滤波过程，降低自身传感器估计精度，进而通过信息交流影响网络中其他传感器的估计性能，导致整个传感器网络目标跟踪效果不佳[17-18]。

本节利用传感器网络中多个传感器的探测信息减少错误量测对跟踪过程的不良影响。错误量测对滤波过程的影响在于，错误量测会给予预测值一个错误的修正从而增大状态估计值相对于真实状态的偏差。考虑各传感器对同一目标t刚确定量测的情景，此时WSN中有多个量测，每个量测都可能是错误的，网络中各传感器均发送自身量测值zi,t(k)，并接收邻居节点的量测值zj,t(k)，j∈Ni（Ni为零距界点集合）。与常用一致性迭代不同的是，本算法所采取的一致性协议为局部平均，传感器网络量测信息交互之后，进行局部平均，即求自身量测和邻居节点量测的平均值。对同一目标来说，多个杂波之间是没有任何关联的，而不同传感器的真实量测之间存在关联。若多个量测全为杂波，其均值是最接近波门中心（预测值）的，此时以保守方式来削弱杂波对预测值的修正。若多个量测中部分为杂波，部分为真实量测，真实量测之间因为存在关联性而差距较小，这些真实量测的值分布得更加集中，而杂波之间没有关联，分布得很分散。此时的均值为更加接近真实量测的值。若多个量测均为真实量测，分布式WSN 中的局部平均能发挥和一致性迭代相似的作用。

由上述分析可知，网络中各传感器量测信息交互之后，采用局部平均的方式能很好地抑制多种量测情况下错误量测对状态估计过程的影响。为进一步加强抑制效果，对此过程进行L1次迭代：

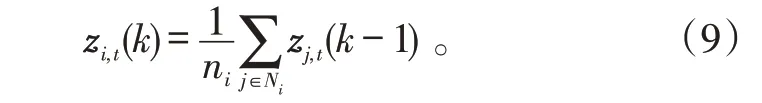
经过此量测一致性迭代，能够得到比较准确的目标t量测，解决了杂波干扰下的数据互联问题。

2.3 基于局部平均的信息一致性

算法的滤波过程基于文献[5]的信息一致性，在完成量测一致性迭代之后，利用最终的量测值更新信息矩阵和信息向量：

式（10）、（11）中：n是网络中传感器的数量；和分别表示传感器i中目标t的信息矩阵和信息向量。

与上一节做同样考虑，为抑制杂波形成的错误量测对滤波过程的干扰，对信息矩阵和信息向量做一致性迭代时，亦采用局部平均作为一致性协议。对信息矩阵和信息向量做L2次一致性迭代：

最后，用信息矩阵和信息向量求得状态估计值和状态估计协方差：

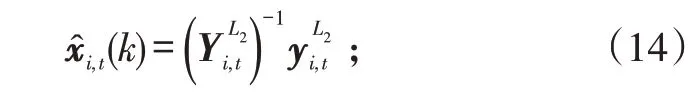
3 仿真实验与结果分析

3.1 仿真实验设置

为验证算法的有效性并对比其性能，设置传感器网络跟踪多目标的实验，3 个目标在同一块区域内匀速运动，它们的运动互不影响，但存在航迹交叉。选取基于最近邻域的信息加权一致性滤波算法[19]（Information weighted consensus filters and their application in distributed camera networks，DN-IWCF）作为对比算法，2 种算法的区别仅在于是否实施量测一致性和局部平均，从而可以充分体现本文所提方法在杂波干扰下的优越性能。

为避免实验的偶然性，得到客观的实验结果，在目标真实运动不变的前提下，用随机Monte Carlo循环求平均的方法获取实验中各项性能指标的均值，设置Monte Carlo循环次数为100次。

图1 多目标运动轨迹Fig.1 Motion trajectory of multi-target

3.2 仿真结果及分析

图2～4分别展示了传感器网络在2种算法的作用下跟踪多个目标的位置误差、速度误差和不一致程度。相应地，表1～3用数据准确说明了3个目标3种误差各自的平均情况。

综合实验效果图和实验数据，在杂波干扰下的简单运动目标跟踪任务中，本文所提算法MC-DMMTA对3 个目标的跟踪精度和一致性程度都要优于DNIWCF，特别是一致性程度有明显改善。2种算法的主要区别在于MC-DMMTA通过量测一致性减少了错误量测导致的跟踪性能下降，而DN-IWCF 易受杂波干扰。可以得出，本文所提出的MC-DMMTA 能非常有效地抑制杂波对传感器网络跟踪性能的影响。

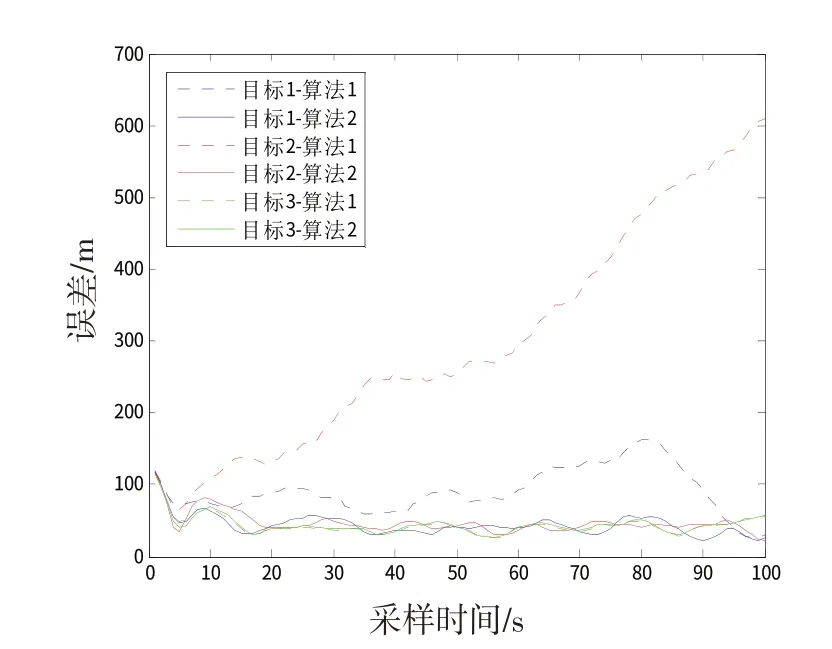
图2 多目标跟踪位置误差Fig.2 Position error of multi-target tracking

表1 2种算法的位置误差Tab.1 Position errors of the two algorithms

图3 多目标跟踪速度误差Fig.3 Multi-target tracking speed error

表2 2种算法的速度误差Tab.2 Speed errors of the two algorithms

图4 多目标跟踪不一致程度Fig.4 Inconsistency of multi-target tracking

表3 2种算法的不一致程度Tab.3 Inconsistency between two algorithms

4 总结

本文探究了基于WSN的分布式一致性跟踪中的多目标跟踪问题。在采用简易数据互联方法的基础上，针对传感器网络跟踪多目标过程中数据互联易受杂波影响，从而误判杂波为量测的情况，对网络中各传感器当前时刻确定的量测做一致性迭代。通过局部平均交互所有量测信息，利用多传感器中正确量测的关联性削弱可能出现的错误量测，对预测值的错误修正，保证后续滤波过程中的估计精度。提出了基于量测一致性的分布式多传感器多目标跟踪方法，设置了杂波干扰下的传感器网络多目标跟踪实验，对比了NN-IWCF 与MC-DMMTA 的跟踪性能。实验结果表明：MC-DMMTA 能有效抑制因误判产生的错误量测对跟踪过程的干扰，可以实现良好的传感器网络跟踪精度和估计信息一致性。