培养质疑习惯，从不盲信中考题开始

■叶新和

（作者单位：江苏省泰州市高港区教师发展中心）

教师具有良好的质疑习惯，是培养学生质疑习惯的基础和前提。培养教师的质疑习惯可以从不盲信中考题开始。

中考题都是优秀试题吗？我们不妨来看看某地的一道中考试题：

如图1，在△ABC中，点D在边BC上，∠ABC∶∠ACB∶∠ADB=1∶2∶3，⊙O是△ABD的外接圆。

（1）求证：AC是⊙O的切线；

（2）当BD 是⊙O 的直径时（如图2），求∠CAD的度数。

图1

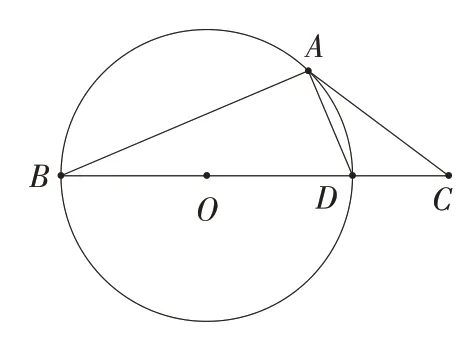
图2

某杂志上一篇文章的解答思路为：

（1）若AC是⊙O的切线，则其应与过切点的直径垂直。过AC与⊙O的交点作一条“直径”，证明该直径与AC垂直即可。

由此，如图3，连接AO并延长，交⊙O于点M，则AM 为⊙O 的直径，连接DM。由已知条件得出∠ABC=∠CAD。由直径所对的圆周角为直角得出∠ADM=90°，证出∠AMD=∠ABC=∠CAD，得出MA⊥AC，即可得出结论。

图3

（2）因为BD 是直径，可知其所对的圆周角∠BAD=90°，再根据∠ABC∶∠ACB∶∠ADB=1∶2∶3，得出∠ABC=22.5°，利用（1）的结果得出∠ABC=∠CAD，从而得出本小题的结论。

仔细分析该思路，发现存在两个问题：

一是该思路中有一个“回路”。即第二小题在求∠ABC的度数后，∠ADB与∠ACB的度数也出来了，直接利用内外角的关系即可求出∠CAD的度数（∠CAD=∠ADB－∠ACB=22.5°），该解答跟第一小题毫无关系。

二是第一小题的解答并不容易。因为由条件“∠ABC∶∠ACB∶∠ADB=1∶2∶3”，能够得到的数量关系比较多，可以有：①∠ACB=2∠ABC；②∠ADB=3∠ABC；③∠ACB∶∠ADB=2∶3；④∠ADB=∠ABC+∠ACB等。能够建立的数量关系越多，解答者越容易无所适从。

将第二小题解答中的“回路”去掉后，第一小题不容易解答显得更为突出。

一、学生试答实验

第一小题解答不容易的判断是否正确？下面的实验比较有说服力。笔者做了一个实验：将原试题拆分为两道试题，与原试题一起，每题都分别让好、中、差3个层次的学生来完成，每个层次选3人，同一层次学生的数学水平尽可能相当。第一题用时10分钟，第二题用时6分钟，第三题用时5分钟。

题目1：上述中考试题。

题目2：如图1（见上页），在△ABC 中，点D在边BC 上，∠ABC∶∠ACB∶∠ADB=1∶2∶3，⊙O 是△ABD的外接圆。求证：AC是⊙O的切线。

题目3：如图2（见上页），在△ABC 中，点D在边BC 上，∠ABC∶∠ACB∶∠ADB=1∶2∶3，⊙O 是△ABD 的外接圆。当BD 是⊙O 的直径时，求∠CAD 的度数。

实验结果如下：

第一题有2 人解答正确；有1 人第一小题解答正确（篇幅15行），第二小题没有做完；有1人第一小题空着，第二小题解答正确（利用内外角的关系解答的）。

第二题只有1人解答正确。

第三题有6 人解答正确；有1 人思路正确，但中间过程计算错误。

二、实验结果说明

从学生解答的正确率来看，第三题明显高于第二题，这说明原题中第二小题远比第一小题要简单得多。此外，在第一题的解答中，有学生利用内外角关系来求解第二小题，而将第一小题空着，据此也能得出同样结论。

综上，可以看出，试题的效度、区分度有问题。第一小题的难度远高于第二小题的难度，命题者考查的意图其实没有达到，试题的有效性难以令人满意。

三、盲信考题带来的问题

中考是指挥棒。若对本题持欣赏态度，更大的问题可能在于对今后教学的不良影响。从前面分析可以看出，解答本题的关键在于解答好第一小题。那么，从一线教师的角度，如何来提高学生得分率呢？可以想象，跟学生讲了弦切角定理（由AC 为切线，得∠ABC=∠CAD）及其逆定理（由∠ABC=∠CAD，得AC 为切线）之后，如果教师再告诉学生：一般来说，由圆中角的数量关系来证明切线，通常用弦切角定理的逆定理来解决，那么对于中等程度的学生而言，本题能够很快得到解决。

然而，弦切角定理及其逆定理是数学课程标准中删去的内容。一般来说，各地的中考考试说明上都会要求不超标，对于课程标准删去的内容，教师坚决不讲。

就上题而言，如果教师严格按照考试说明来教学，会吃亏，讲了课标中删去的内容能够“沾光”。如此一来，严格按照课标、教材与中考考试说明的要求来进行教学的教师估计将越来越少，慢慢就变成上有政策、下有对策，从而导致相关政策的公信力将不复存在。