阅读中学习新知 理解中解决问题——由数学阅读理解型考题引发的思考

■张建良

（作者单位：江苏省常熟市兴隆中学）

阅读是自我发现的过程，也是自我学习的过程。初中阶段是人生阅读素养发展和提升的关键期。帮助提高初中生的阅读素养水平不仅要在语文学科中推进，也需要其他学科跟进，通过跨学科的阅读进一步提升学生的综合阅读理解能力。那么如何在数学学科中指导学生进行数学阅读？如何建设适合学生的数学阅读课程？本文基于这些思考，借助阅读理解型考题，思考如何进行数学阅读教学和数学阅读课程建设。

一、考查学生学习新概念，运用新知识的能力

有类新概念与初中学习过的知识有着紧密的关联或者是自然的延伸，题中出现的新概念也是今后学生在高中阶段将要学习的内容。这类阅读理解题的考查目的是让学生在有限时间内自学一个新概念，从对新概念的理解到运用，其过程恰好考查了学生自主学习和运用新概念的能力。下面的试题就是以初中知识中的指数运算为出发点引出新概念——对数。

例1（2018·四川自贡）阅读理解：对数的创始人是苏格兰数学家纳皮尔（1550年-1617年），纳皮尔发明对数是在指数书写方式之前，直到18 世纪瑞士数学家欧拉（1707 年-1783 年）才发现指数与对数之间的联系。

对数的定义：一般地，若ax=N（a〉0，a≠1），那么x叫做以a为底N的对数，记作：x=logaN。比如指数式24=16 可以转化为4=log216，对数式2=log525可以转化为52=25。

我们根据对数的定义可得到对数的一个性质：log（aM·N）=logaM+logaN（a〉0，a≠1，M〉0，NN〉=0a）n；，理∴由M·如N下=a：m·设anl=oagmaM+n，=由m，对l og数aN的=n定，则义M得amm+，n=log（aM·N），又∵m+n=logaM+logaN，∴log（aM·N）=logaM+logaN。解决以下问题：

（1）将指数43=64转化为对数式________；

（3）拓展运用：计算log32+log36-log34= ____。

解答这个新概念型阅读理解题，学生首先要关注指数运算与对数运算之间的关系，求对数可以转化为求“指数”，特别需要学生在对数和指数之间来回切换。第（1）小题答案为3=log464。其次还要正确理解对数性质的证明过程，从同底数幂相乘出发完成第（2）小题的证明。若要完成第（3）小题，学生还需要对公式从右到左方向去运用，考查学生逆向思维水平，计算结果为1。

该考题不但考查了学生的数学理解能力，而且也考查了运用新知识的思维水平。从另一个侧面检测了教师在平时的教学中有没有对学生的自学能力培养落实到位，学生如果平时没有阅读数学教材的习惯，那么遇到此类阅读理解题将会无所适从。为此，让学生自学，让学生独思，让学生讨论，应成为数学课堂教学中的关键场景。同时这类考题还让学生了解了对数的由来，感受到一些数学史。

为此，在阅读教学中，教师应指导学生主动划出暂时不理解的内容，再去复读、分析、理解，促进学生对新的数学符号、术语及其含义的正确理解。同时，在平时的阅读教学过程中，让学生多一点对教材中数学概念的阅读和交流，有意识地增强课内阅读频率，提高思维敏锐度，提高阅读的速度和质量。

二、考查学生学习新定义、解决新问题的能力

有类考题虽没有教科书式的数学概念表述，但会用数学符号创设新的数学表达式，给出新定义。这类阅读题考查了学生能否迅速抓住新数学符号的表达含义，考查了学生对新信息的提炼和加工转化能力。由于学生第一次见到这类新定义题目，不仅要求学生对数学符号了如指掌，也要求其对数学表达式的结构、运算等有清晰的理解。阅读时学生要明白新出现的知识和已知知识之间的联系是什么，特别要理解题中所举例子的解答过程，它将成为自我解决问题过程中被模仿的对象。只有当学生对所给的阅读材料全面深刻理解后，才能完成后面所有要回答的问题。

例2（2018·四川内江）阅读理解：对于三个数a，b，c，用M{a，b，c}表示这三个数的中位数，用max{a，b，c}表示这三个数中的最大数，例如：

M{-2，-1，0}=-1，max{-2，-1，0}=0，max{-2，-1，

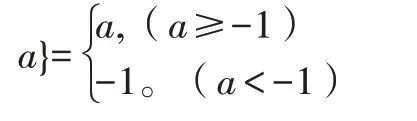
解决问题：

（1）填空：M{sin45°，cos60°，tan60°}= ____，如果max{3，5-3x，2x-6}=3，则x的取值范围为___；

（2）如果2·M{2，x+2，x+4}=max{2，x+2，x+4}，求x的值；

（3）如果M{9，x2，3x-2}=max{9，x2，3x-2}，求x的值。

这样的阅读理解考题——新定义型，专注于考查学生的数学符号意识和对所举例子的阅读理解能力。阅读过程中，一是要理解题中名词“中位数”“最大数”；二是要观察两个数学新符号：M{ }，max{ }；三是要观察所举例题max{-2，-1，0}和max{-2，-1，a}中的一个“0”变为“a”所引起的结论变化。这时学生必须自觉地提出问题：为什么此时最大数会出现两个答案？进一步获得一个重要信息，就是对a与-1要进行大小比较，这进一步考查了学生分类讨论的意识。学生同时利用题中的特殊情形启动思维，再在一般情形中深化理解。

这样的考题，促使教师在阅读教学中，要多引导学生理解文字说明和符号表达，多与题中的信息进行交流，其过程是一次不断自问自答的过程，然后筛选出有用的信息去解决新问题。当然阅读同样的信息，对于不同的学生，不同的方法，效果完全不同，其差距的根本在于一个学生是否真正理解并获取了正确信息，是否重新组织、存储并转化了信息。因此学生要提升阅读水平，必须不断渗透问题意识。阅读质量的高低关键还在于自我提问的质量。

三、阅读理解型考题引出的教学思考

1.通过数学阅读素材的收集，建设初中数学阅读课程。

数学阅读材料应紧扣有关知识点，短小精悍，集知识性、科学性、趣味性、教育性于一体，可涉及数学史料、数学家的故事、数学轶闻、自然科学等多方面知识，是对教材教学内容的延伸和扩展，不仅丰富了教学内容，开阔了学生视野，而且也利于提升学生的数学核心素养。

为了了解目前数学阅读情况，笔者曾对两个班级学生进行一次问卷调查，其中一个多选题为：你在数学阅读方面遇到了哪些困难？

A.学习任务重，没时间；B.基础知识不牢固，没底气；C.不爱看书，没习惯；D.数学内容读不懂，没办法；E.找不到感兴趣的数学读物，没推荐；F.阅读方法不正确，没方法。

统计结果表明，选择E 选项的人数最多，接近80%，两个班的选择人数比较一致。由此看出，为学生建设数学阅读的相关课程显得极为必要。在教学中利用阅读课程资源让学生进行学习，可促进学生独立思考问题、提出问题。教师除了自己创建一些课外阅读课程资源外，也要充分利用好教材上的阅读资源。教材中的“阅读”内容更多展示了对当前所学知识的扩充和补充。比如苏科版初中数学教材中就安排了“谈一谈”“阅读”和“读一读”等内容，为学生阅读提供了有效灵活的素材。这些阅读材料是对本章相关知识背景的延伸和补充。但对于这些内容的阅读，有时师生就采用扫描式阅读，即在一定的时间范围内，尽快地看一遍，阅读的目的大多设定为拓展一下学生的知识面，激发一下学生的数学兴趣而已，这样的数学阅读也只是一次简单的了解而已，并不能提升学生数学阅读的水平。当然，教材不是阅读的全部，要想从阅读中获得更高的价值或回报，我们还需多做数学阅读课程的建设，设计一条阅读路径及与其相匹配的课程内容，尤其可以通过积累微课和阅读理解型考题，获得适合学生数学阅读的内容素材，让学生从视频和考题中给出的一个个设问中学会理解运用新概念，积累如何在阅读中理解数学概念的方法，实现以题促读，以读促学。

2.通过数学阅读方法的训练，培养学生对信息的转化能力。

数学阅读是指从公式、图形、符号、文字等数学材料中提取信息并加工的过程。在这个过程中，需要身体各个感官的全面参与，通过眼睛捕获信息，大脑进行精加工完成阅读理解过程。数学阅读过程中，由于数学语言的抽象性，要求阅读者有较强的逻辑推理能力，数学语言的严谨性要求阅读者将口、手、脑同步使用，数学阅读者不但要读文字、图表、数学符号，而且要能够对文字、图形、符号进行及时转换。在阅读过程中，学生要不断地提出“为什么”，以此推动问题导读。没有问题的阅读只是一次扫描式的阅读，有阅读行为而无理解和收获。因此阅读者在看材料时要会提出问题，还要对所阅读的内容进行推理、归纳等。在数学阅读中，可以将阅读理解看作阅读分析，通过分析获得真正的理解。阅读教学中教师要注重创设学生阅读交流的平台，让每一位学生在小组内进行交流，相互介绍阅读的方法与疑问，教师再加以引导和点拨。在学生相互交流与教师的点拨中不断提升学生阅读理解水平，实现以议促读，以读促思。

数学阅读教学关键在于引导学生主动提出问题和自我思考问题。例如现在正在阅读的这个内容到底讲什么？有什么地方不能理解？阅读的内容与自己脑子里的原有的知识有什么样的联系和变化等。其实不管选择哪种方式进行阅读学习，只有跟学生的原有知识结构和理解能力连接起来，才有意义和价值。因此，如果要获得超越一般阅读的阅读层次，那么学生在整个阅读的过程中就要不断地进行自我提问，再通过反复咀嚼和消化，这一段阅读内容才能转化为学生自己的理解。基于此，在数学教学中教师首先要重视利用教材、微课和试题等内容来建设适合初中生阅读的课程，通过课程建设推进学生数学阅读素养的提升；其次，阅读时教师要有方法指导，在阅读过程中让学生有意识地关注问题的收集、分析和归纳，不断提高阅读过程中思维的敏锐度和深度。一个良好的阅读习惯，将会使学生各方面的素养得以提升。