基于闪烁现象的旋翼微动特征提取方法
(空军预警学院, 湖北武汉 430019)
0 引言
武装直升机由于其本身独特的优点,已经成为了现代空袭作战中的“杀手锏”,而直升机旋翼作为典型的微动目标,已经受到国内外学者的广泛研究[1-6]。文献[7-8]通过电磁仿真和实测数据指出旋翼目标回波中存在闪烁现象,但是当前窄带雷达对旋翼特征进行提取主要是在旋翼回波不发生闪烁情况下进行的[9-13],如时频分析方法[9]、正交匹配追踪算法[9]、Hough变换法[9]、高阶矩函数分析法[10-11]以及函数构建法[12]和自相关法[13]。其中正交匹配追踪算法、高阶矩函数分析法需要用到回波的相位信息,而Hough变换存在着计算量大,无法快速进行转速估计,函数构建法虽然计算量较小,但是在旋翼散射点均匀分布时会失效,而自相关法必须在叶片个数已知的情况下才能准确估计旋翼转速。因此,大部分现有的旋翼目标特征提取方法并不符合旋翼回波中存在闪烁的实际,闪烁情况下的旋翼目标特征提取方法仍需进一步研究。
针对上述问题,本文提出了基于闪烁现象的旋翼微动特征提取方法,根据旋翼回波中闪烁的时域特点和时频域特点,通过自相关处理估计出回波的闪烁间周期,利用时频分析和骨架提取方法判断叶片的奇偶数及估计旋翼目标的最大微多普勒频率,然后通过闪烁周期与叶片数和转速的关系,估计出目标转速的多种可能值,并同时计算不同转速情况下的叶片尺寸估计值,然后通过先验区间对转速和尺寸的估计值进行初步选择,利用选择结果对信号在相同噪声大小的情况下进行重构,将重构信号能量与原始信号能量最接近的估计值作为最终的特征提取结果,进而完成对闪烁条件下旋翼微动特征的提取。
1 旋翼微动目标信号建模分析
基于窄带雷达,在观测时间较短的情况下,旋翼目标不会出现距离单元走动,若观测时间较长,旋翼目标出现距离单元走动现象,此时对旋翼目标进行运动补偿后,旋翼目标的运动状态可等效为悬停状态[14]。为简化分析,假设目标与雷达处于同一个平面,如图1所示,雷达到旋翼目标旋转中心的距离为RC,假设旋翼微动目标为散射点模型,旋翼某一个叶片上的散射点P到旋翼中心的距离为r(0≤r≤l,l为旋翼叶片长度),P点到雷达的距离为RP,同时P点以角速度ω绕旋转中心C旋转,初始时刻P点的初始旋转角为θ。

图1 旋翼目标模型
旋翼目标经过脉冲压缩后的视频回波信号为[15]
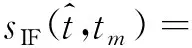
(1)

Rij(tm)=RC+rijcos(2πfrottm+θij)
(2)
式中,rij为叶片上各散射点到旋转中心的长度,frot为旋翼目标的转动频率,θij为叶片上各散射点的初始相位。
由式(1)、式(2)可知,散射点的微多普勒呈现余弦函数形式,而余弦函数的周期与旋翼旋转周期是一致的。且不同叶片上散射点引起的微多普勒曲线有着不同的初相,而同一叶片散射点初相是一致的,差异在于多普勒频率峰值大小的不同,旋翼目标瞬时微多普勒频率为
(3)
当旋翼目标处于悬停状态时,从推力平衡性考虑,多个旋翼叶片的转速是相同的,转速误差不会超过1 r/min,表明此时旋翼回波只有一个调制周期特征[17]。理论和实际都证明,当雷达视线方向与旋翼叶片垂直时,回波的幅度最强,当偏离垂直方向时,回波的幅度锐减,从而形成闪烁现象[7-8]。
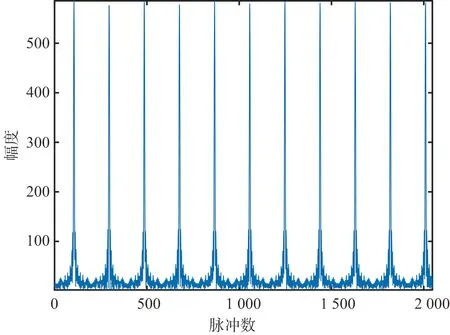
图2 时域闪烁现象示意图
当旋翼叶片采用式(1)所示的散射点模型时,还需要满足单个叶片上的散射点间隔小于波长的一半,否则不会出现闪烁现象[6]。当出现闪烁时,其闪烁脉冲信号的形状是由慢时间轴上的sinc函数给定的,其脉冲闪烁周期Tint[18]满足
(4)
由于旋翼目标产生的这种具有周期性的闪烁脉冲信号,可以将慢时间维的旋翼目标回波信号看作周期平稳或循环平稳信号,这种特征为旋翼目标的检测与特征提取提供了有利条件。
2 旋翼目标微动特征提取
本文提出的基于闪烁现象的旋翼微动特征提取方法共分四步:第一步是寻找含有旋翼目标信号的单个距离单元,对其进行傅里叶变换估计出旋翼目标的闪烁周期;第二步是利用时频分析和图像骨架[3]提取的方法估计出目标的最大瞬时多普勒频率以及旋翼目标叶片的奇偶数;第三步是利用前两步的结果,找出叶片数、转动频率和尺寸三者可能的组合;第四步是估计出回波信号中噪声的功率,利用第三步的结果对回波进行重构,并在重构信号中添加与回波中相同功率大小的噪声,然后对比原始回波信号与重构信号的能量,能量最接近的重构信号所包含的特征即为旋翼目标的特征。
2.1 闪烁周期估计方法
在窄带雷达回波中,旋翼目标不会出现距离单元走动,那么含有旋翼目标信号的通常只有一个距离单元,在噪声中寻找到这个距离单元是本文的基本前提。因此,本文利用能量门限选择该距离单元,门限η定义如下:
(5)
式中,Ed表示第d个距离单元的能量,Em表示所有距离单元的平均能量。当某个距离单元的能量低于门限η,则表示该距离单元只包含噪声,当能量高于门限η,则表示该距离单元是旋翼目标所在的距离单元。对该距离单元进行自相关处理,表达式可写为
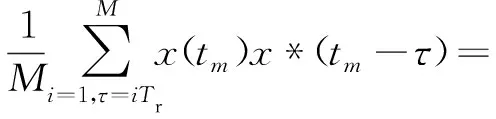

(6)
式中,s(tm)为旋翼目标的回波方位向信号,n(tm)为噪声,x(tm)=s(tm)+n(tm),从式中可以看出进行自相关处理后噪声的幅度变为原来的1/M,能够有效地提升回波的信噪比,使用该方法估计闪烁周期具有良好的抗噪性能。此时闪烁周期为
(7)
式中,τ1为R(τ)取最大值时的时延值,τ2为R(τ)取次最大值时的时延值。
2.2 最大微多普勒频率估计方法
采用局部分析方法即时频分析来对旋翼目标所在的距离单元进行处理,可以得到其慢时间与微多普勒频率的关系。STFT是最常用的基于匹配滤波的时频分析方法,当STFT选取的窗函数为高斯窗时,称之为Gabor变换,根据测不准原理,Gabor变换具有最佳的时频分辨率。
对式(1)进行Gabor变换可以得到微动目标信号的时频图,其表达式[9]为
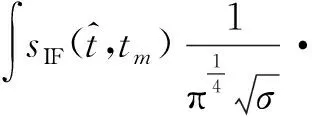
(8)
对具有时域闪烁现象的旋翼微动回波信号进行时频分析,同样会在时频域出现闪烁现象,且闪烁的峰值对应旋翼目标的最大微多普勒频率。时频闪烁示意图如图3所示。
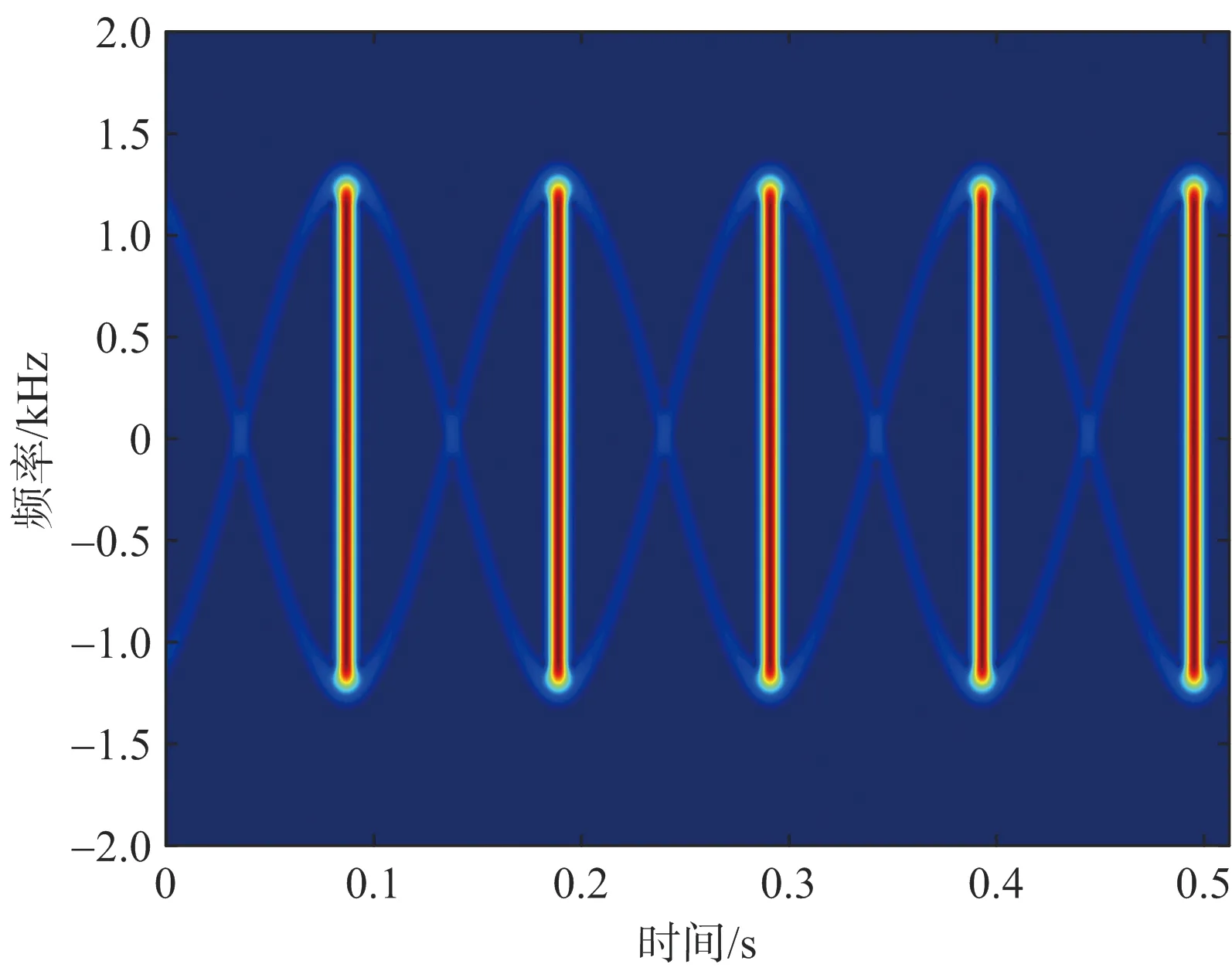
(a) 偶叶片

(b) 奇叶片图3 时频闪烁现象示意图
由于时频分析受到其分辨率的影响,直接提取参数的误差较大,为了减少后续处理的运算量以及提高参数提取的准确度,从图像域的角度出发,对时频图图像进行阈值处理、平滑处理和二值化处理,而后提取出闪烁位置的时频曲线骨架,此时的图像矩阵中只包含“0”和“1”两个值,其中“1”出现的位置即为时频曲线的骨架,此时可以通过时频图骨架准确提取出微动目标的最大瞬时微动频率,并且通过判断闪烁在正负频率图像上是否对称来估计旋翼目标叶片的奇偶数,若正频率图像与负频率图像对称,即可判断为旋翼目标的叶片数为偶数,若不对称,则为奇数。
热点分析法属于局部自相关分析方法,根据在一定分析规模内的所有要素,计算每个要素统计值,得到每个要素的z值和p值[35],通过热点分析,可以识别出老年人口高、低值在空间上聚类的区域,公式如下[31]:
在估计出旋翼叶片的奇偶数后,可以进一步估计得到目标的尺寸:
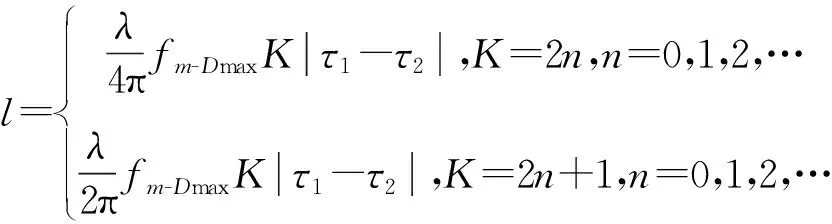
(9)
估计得到尺寸之后,可以完整地得到关于叶片尺寸、转动频率以及叶片数的多种组合,这些组合具有相同的时域闪烁和时频域闪烁特征,根据现有公开资料[19-20],直升机旋翼的叶片数基本是 2~8个,叶片的尺寸处于5~12 m,旋翼转动频率在3~7 Hz之间。利用这个先验条件,对多种可能组合进行初步的筛选,可以得到符合实际情况的几种组合,如图4所示,当叶片数为偶数时,相同闪烁频率情况下,最多只有3种可能的转动频率,并分别对应不同叶片数,当叶片数为奇数时,最多只有2种可能的转动频率。因此,经筛选后可能组合最多只有3个。

(a) 偶叶片
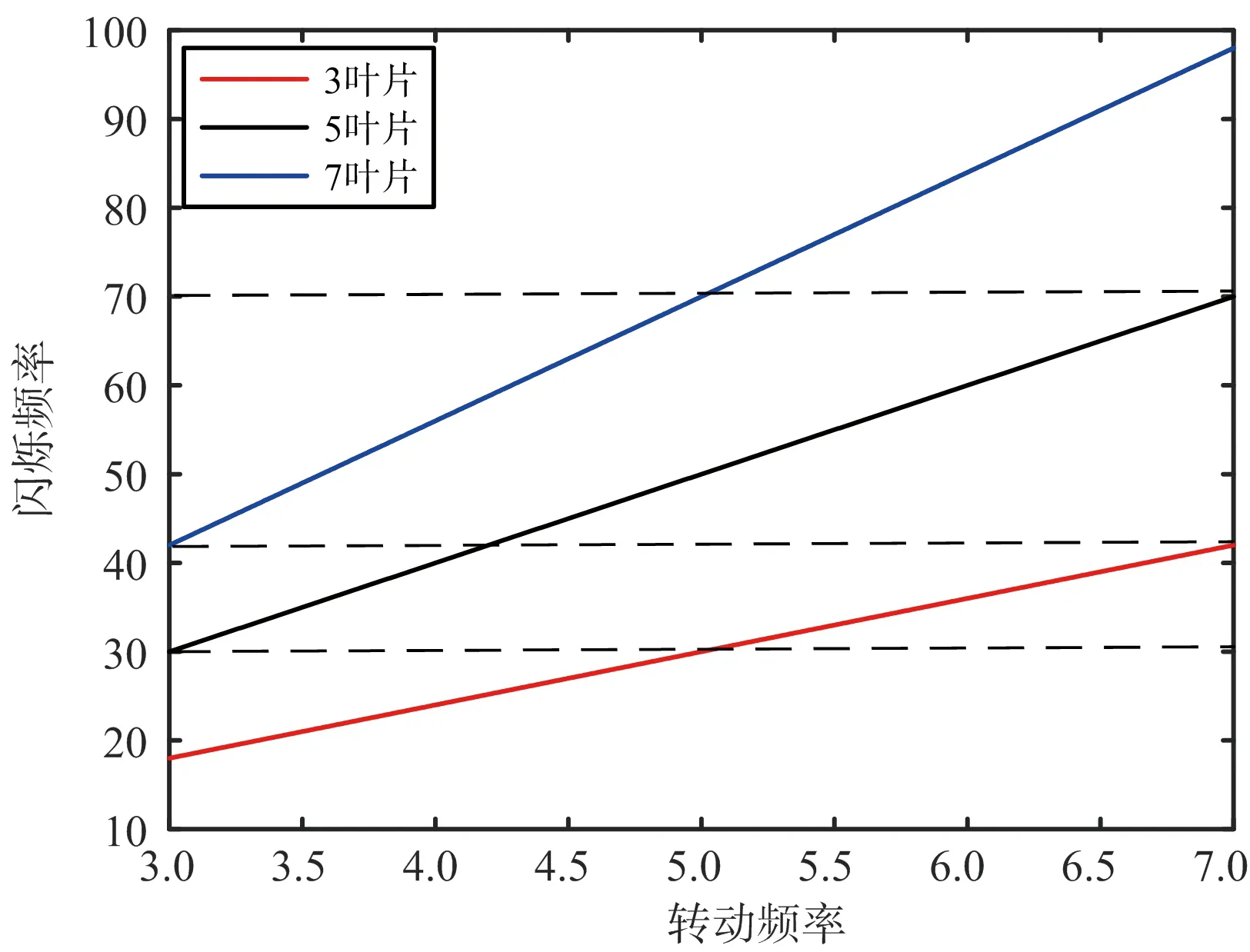
(b) 奇叶片图4 多值区间
2.3 信号重构方法
利用式(5)中得到的门限η,选择出只包含噪声的距离单元,计算这些距离单元内噪声的平均功率:

(10)
式中,M为脉冲数,Dn为只包含噪声的距离单元,Sn为这Dn个距离单元的噪声。
在估计出回波信号中噪声的平均功率后,将2.2节初步估计得到的关于叶片尺寸、转动频率以及叶片数的多种组合作为先验知识,利用式(1)对不同组合的回波进行时域重构,且添加噪声功率的大小与真实回波信号中包含的噪声功率大小保持一致,此时重构信号表达式可写为

(11)

对信号在相同噪声功率大小下进行重构后,由于这些重构后的信号具有相同的时域闪烁和时频域闪烁特征,所以依然无法找出目标组合,但是由于每个组合中的叶片数是不相同的,若每个散射点反射系数相同,散射点间隔d=λ/3(一定会出现闪烁现象),其时域回波的能量是不相同的,因此,可以根据重构信号能量与回波信号能量的相似程度来准确估计叶片数目,从而找出目标组合。
基于闪烁现象的旋翼微动特征提取方法具体流程如图5所示。

图5 算法流程图
3 仿真分析
为了更加清晰得到本文方法对微动目标转动频率(frot=ω/2π)、尺寸和叶片数的提取,仿真选择了几种典型直升机的真实数据作为目标参数,仿真信噪比为脉压后10 dB。为了满足方位向采样条件PRF=4ωl/λ,以及在观测时间内至少获得2次时域闪烁,仿真参数设置如表1所示,目标参数如表2所示。

表1 仿真参数

表2 目标参数

(a) 时域闪烁结果

(b) 自相关处理结果

(c) 时频域闪烁结果

(d) 骨架提取结果图6 AH-1W特征提取结果
利用AH-1W直升机真实参数进行仿真,其仿真结果如图6所示。从图6(a)可以看出,此时回波中出现了明显的时域闪烁现象,对其进行自相关处理结果如图6(b)所示,根据图6(b)中峰值位置与次峰值位置的时延可以估计出此时闪烁间隔为0.102 s,对其进行时频分析可以得到图6(c)所示结果,其闪烁出现的位置与时域闪烁位置相同。与图3不同的是,由于在回波中添加了噪声,能够体现出叶片数量的正弦调制曲线完全被淹没在了噪声背景中,因此此时无法直接从曲线的条数对叶片数进行直观的判断,对图6(c)所示结果进行骨架提取得到图6(d)所示结果,此时可以判断此时旋翼叶片数量为偶数并估计出目标最大瞬时微多普勒频率为1 488.4 Hz。根据闪烁间隔、叶片数(偶叶片数只考虑2,4,6,8个)与闪烁周期的关系,可以得到闪烁周期可能值为0.204 3 s,0.408 5 s,0.612 7 s,0.817 0 s,那么对应的转速可能值为4.896 0 Hz,2.448 0 Hz,1.632 0 Hz,1.224 0 Hz,根据式(9)可以计算出目标尺寸可能值为7.238 0 m,14.476 0 m,21.713 9 m,28.951 9 m,此时通过判断叶片尺寸和旋翼转速是否满足设置区间来对可能值进行筛选,符合区间仅有一组值,叶片长度为7.238 0 m,旋翼转速为4.896 0 Hz,叶片数为2个。由于符合设置区间的仅有一组数据,因此不需要利用估计值对信号进行重构来进一步进行判断,此时尺寸估计误差为0.849%,转速估计误差为0.082%。
利用SA341直升机真实参数进行仿真,其仿真结果如图7所示。根据图7(b)中峰值位置与次峰值位置的时延可以估计出此时闪烁间隔为0.028 s,从图7(d)可看出,此时旋翼叶片数量为奇数并估计出目标最大瞬时微多普勒频率为1 306.6 Hz,根据闪烁间隔、叶片数(奇叶片数只考虑3,5,7个)与闪烁周期的关系,可以得到闪烁周期可能值为0.168 s,0.280 s,0.392 s,那么对应的转速可能值为5.952 4 Hz,3.571 4 Hz,2.551 0 Hz,根据式(3)可以计算出目标尺寸可能值为5.240 5 m,8.734 2 m,12.227 9 m,此时通过判断叶片尺寸和旋翼转速是否满足设置区间来对可能值进行筛选,符合区间有两组估计组,叶片长度为5.240 5 m,旋翼转速为5.952 4 Hz,叶片数为3个以及叶片长度为8.734 2 m,旋翼转速为3.571 4 Hz,叶片数为5个。由于符合设置区间的有两组数据,还需要进行进一步的筛选,因此分别利用两组估计值对信号进行重构,重构信号的能量与原始回波的能量相近的一组估计值即为目标特征的估计值。第一组估计值重构信号与原信号能量偏差为4.96%,第二组估计值重构信号与原信号能量偏差为176.66%,因此选择第一组估计值作为输出,此时与真实参数相比,尺寸估计误差为0.181%,转速估计误差为0.793%。

(a) 时域闪烁结果

(b) 自相关处理结果

(c) 时频域闪烁结果

(d) 骨架提取结果图7 SA341特征提取结果
由于其余3种直升机特征提取的仿真方法相同,仅仅只有仿真参数设置的不同,为简化分析,5种直升机的参数估计结果如表3所示,估计误差如表4所示。

表3 参数估计结果
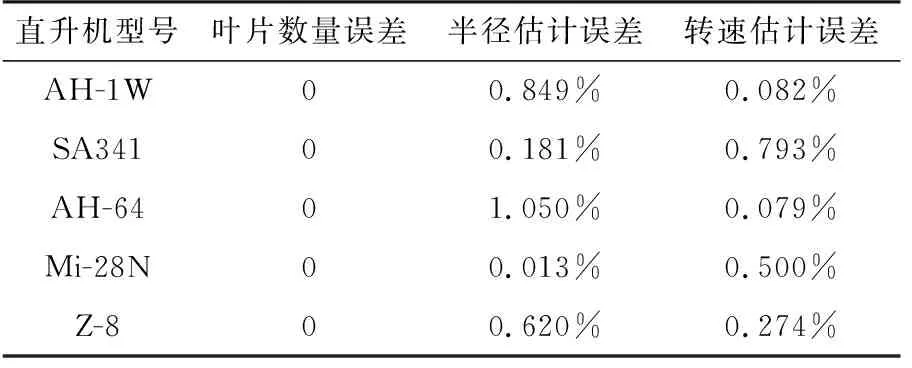
表4 估计误差
从表3和表4可以看出,本文方法能够准确估计出目标的叶片数目,并且叶片尺寸误差和旋翼转速误差都较小,具有较强的稳定性,并且利用本文方法仿真时原始信号与重构信号的初相均为随机相位,因此本文方法可以在不知道目标初相情况下对旋翼目标特征进行提取。
4 结束语
本文提出了一种基于闪烁现象的旋翼微动特征提取方法,该方法通过自相关处理估计出旋翼目标回波的闪烁间隔,并利用闪烁间隔与叶片数的关系估计得到多种可能的闪烁周期,通过对其进行时频分析并提取相应的时频图骨架,判断叶片的奇偶数及估计旋翼目标的最大微多普勒频率,并利用旋翼目标叶片数量、叶片尺寸和旋翼转速所处的大致范围作为先验知识对估计值进行初步筛选,然后在保持与原始信号中噪声功率相同情况下,利用估计值对回波信号进行重构,从能量差异的角度出发对估计值进行第二次筛选,将原始信号能量与重构信号能量最接近的估计值输出作为最终的估计值。通过仿真结果可以看出,本文方法可以准确地估计出旋翼目标的叶片数,旋翼转速和尺寸误差均在可接受范围内。

