基于内定标的高分三号通道误差校正方法
(1.中国科学院电子学研究所, 北京 100190; 2.中国科学院大学, 北京 100049)
0 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)由于其全天候、全天时的成像特性,已被广泛应用于军事、经济等诸多领域[1-2]。目前,同时实现高分辨率和宽测绘带成像是SAR领域一直努力的方向之一,这样不但能够提供目标更为精细的特征信息,而且可以一次性对更大区域进行成像[3]。高分辨率需要足够高的脉冲重复频率(Pulse Repetition Frequency, PRF)来避免方位模糊,宽测绘带则需要低PRF来抑制距离模糊[4],因此在传统SAR系统设计上形成了无法调和的矛盾。为了解决这一问题,方位多通道SAR系统应运而生。它通过在方位向设置多个接收通道来实现。发射低PRF信号来获取宽测绘带,把多个接收通道接收到的回波组合成一个高PRF用来达到高分辨率的目的。然而,实际情况下,外界环境和加工工艺等因素都会使各接收通道的幅相特性存在差异。通道误差将显著降低模糊抑制的性能[4],给后续成像带来影响。因此,通道误差校正是方位多通道SAR系统成像流程中不可缺少的一步。
目前,国内外已经提出很多通道误差校准方法。文献[5]提出了信号子空间比较法和天线方向图法,可以有效估计出通道误差。其中信号子空间比较法适用于各种场景,但需要准确获取回波的协方差矩阵,天线方向图法运算量小,但只适用于均匀分布的场景。文献[6]利用对称的多普勒通道频谱分量的导向矢量共轭相等[7]的特性,提出了一种估计通道误差的方法,然而该方法对系统要求严格,必须为正侧视。文献[8]引入了正交子空间法[9]用于误差估计。文献[10-11]对正交子空间法和其他算法进行了比较,并在仿真实验和机载实测数据上验证了其有效性。上述方法操作都是基于回波数据的处理。目前正交子空间法应用比较广泛。
为了解决通道不平衡的问题,本文提出了一种基于内定标数据估计通道误差的方法。首先从每个接收通道的内定标数据中估计出延迟误差和相位误差,并将其补偿在回波数据上,使得每个通道接收到的点目标回波为一较理想线性调频信号;然后估计和补偿通道之间的幅度误差;该方法考虑了通道本身的误差,同时误差是从内定标数据中估计出来的,减少了算法处理的数据量。高分三号实测数据的处理结果验证了该算法的有效性和鲁棒性。
1 高分三号双通道接收模式下的信号模型
高分三号卫星是国内第一颗具有双通道接收模式的星载SAR。其双通道模式称为超精细成像模式。图1为高分三号双通道接收模型。M为通道数,Rt为目标到发射通道的距离,Rm为目标到第m接收通道的距离(m=1,2,…,M),v为雷达速度,d为相邻通道间的距离。高分三号双通道间距为3.75 m。
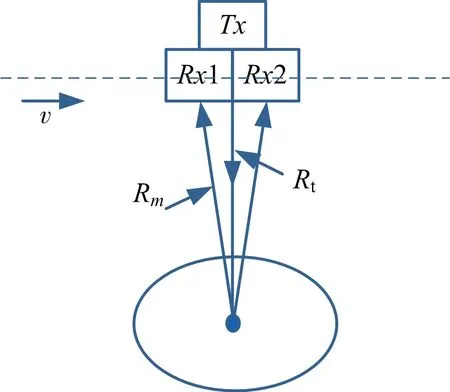
图1 高分三号SAR系统
通过补偿一个常数相位后,每个通道的回波可以等效为在等效相位中心(Equivalent Phase Center, EPC)自发自收的回波[12]。等效相位中心位于发射通道和相应的接收通道的中心。
第m通道接收到的回波信号可以表示为
Sm(τ,η)≈exp(j·φm)·σ·
exp(-j·4π·f0·Rme(η)/c)×
exp(j·π·Kr·
(τ-2·Rme(η)/c-τm)2)×
(1)
式中,τ为距离时间,η为方位时间,φm为第m通道的总相位误差,Rme为目标到第m等效相位中心的距离,c为光速,Tr为发射脉冲的持续时间,f0为载频,Kr为距离向调频率,τm为由通道误差引起的第m通道的时延,x为发射通道和第m通道之间的距离,R0为最短斜距,σ为后向散射系数。
方位多通道SAR系统成像基本流程如图2所示。
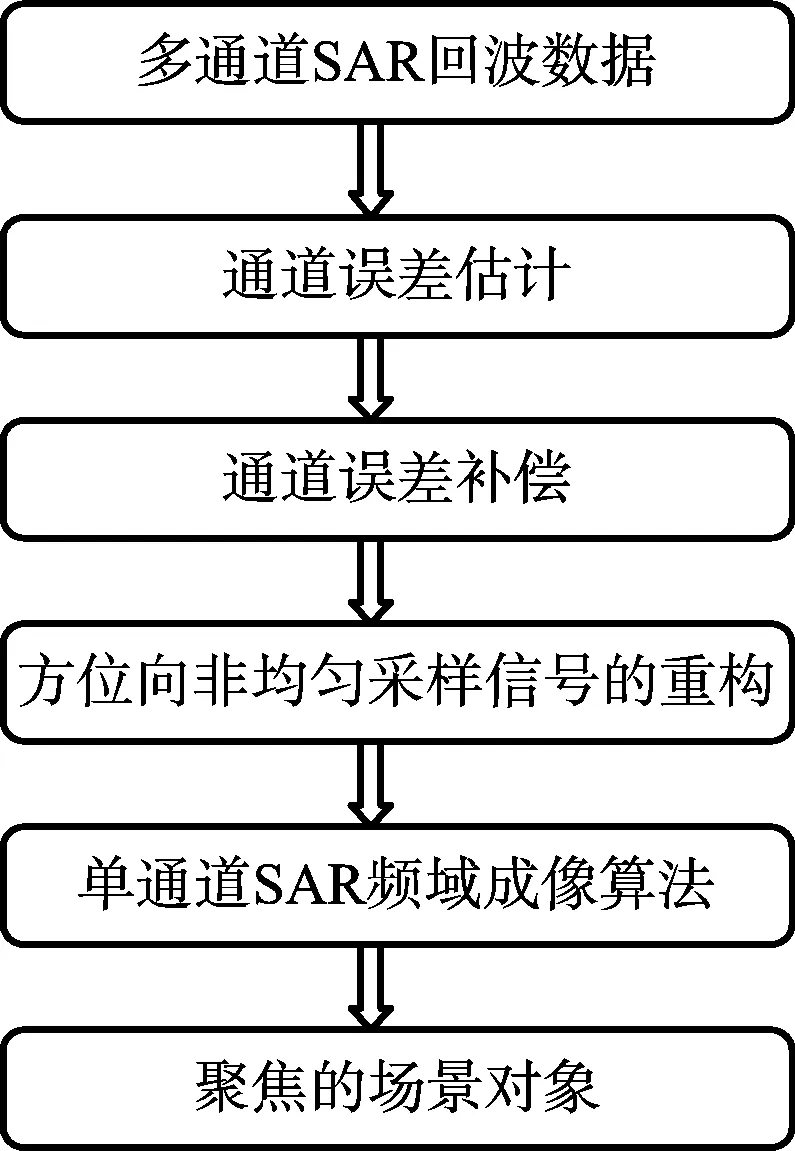
图2 方位多通道SAR系统处理流程
2 基于内定标数据估计和补偿误差
内定标主要用于辐射校正,通常是在雷达系统内部布置测量设备,测量出发射功率和接收机增益误差等,监视雷达系统内部的动态变化,从而校正雷达图像[13]。因此,获取到的内定标数据可以反映信号发生的变化,例如信号的时延、相位变化等。
常规SAR发射线性调频信号(Linear Frequency Modulation, LFM),然后对接收到的回波信号进行距离向和方位向的匹配滤波,从而得到被测区域的雷达图像[14]。在实际情况中,由于SAR系统设备存在误差以及外界环境因素等,每个通道回波信号不再是标准的线性调频信号,存在着时间延迟、幅度误差、相位误差。对于方位多通道SAR系统,不同通道之间还会存在差异。
基于内定标数据估计和补偿误差方法的流程如下:
1) 从内定标数据估计出每个通道的时延和相位误差。
2) 在距离频域用估计出的误差对回波数据进行补偿。
3) 从内定标数据估计出通道间幅度比值。
4) 利用通道幅度比补偿回波数据的幅度误差。
假设理想线性调频信号为
(2)
式中,T为信号的持续时间,A为幅度,K为线性调频率。
内定标信号可表示为
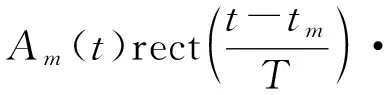
exp(jπK(t-tm)2)·exp(jφm(t))
m=1,2,…,M
(3)
式中,Am为幅度,tm为相对理想线性调频信号的时延,φm(t)为相对理想线性调频信号额外的相位误差。
arg(s(t))=πKt2
(4)
arg(sm(t))=πK(t-tm)2+φm(t)
(5)
Δφ=arg(sm(t))-arg(s(t))=
(6)
式中,Δφ为两信号的相位差。从式(6)可得,Δφ是时间变量t的线性函数。斜率与时延tm有关,可通过此关系求出时延tm,进而通过式(6)求出φm(t)。
获取到每个通道的时延和相位误差后,对回波数据进行补偿。将回波数据距离向傅里叶变换到距离频域。
根据傅里叶变换性质,信号在时域中右移tm,相应地,信号在频域上乘以一个负指数线性相位函数。
g(t-tm)↔G(f)exp{-j2πftm}
(7)
因此,按照式(7)所示操作,在距离频域,回波数据乘以一个线性相位,来补偿延迟。φm(t)在频域变成误差曲线φm(ω)。补偿完时延的回波数据乘以exp(-jφm(ω)),完成相位误差的补偿。
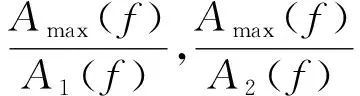
3 高分三号实测数据处理
第2节介绍了基于内定标数据估计和补偿通道误差的方法。估计和补偿完通道误差后,进行方位向非均匀采样信号的重构,将多通道等效为单通道,然后运用常规SAR成像算法即可得到误差校正后的图像。
按照文中算法处理高分三号实测数据。该数据出自中国科学院电子学研究所航天微波遥感系统部。高分三号相关参数如表1所示。
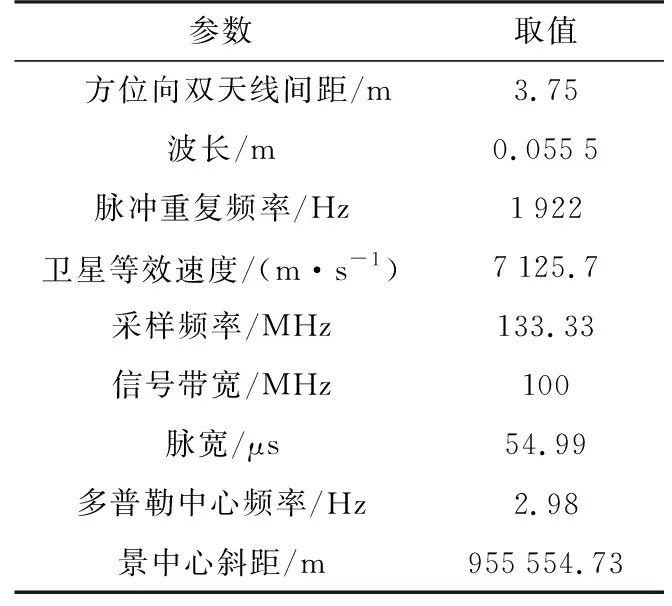
表1 高分三号参数
首先,对每个通道内定标数据所含脉冲的幅度进行了归一化,如图3所示。这里以通道1为例。通道1内定标数据相关参数为脉冲数412,采样点数13 056。
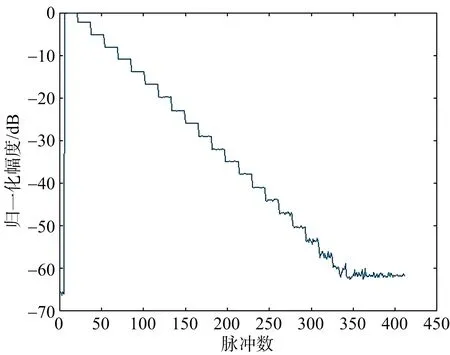
图3 通道1内定标数据脉冲幅度归一化图
选择信号幅度不饱和的第一组幅度较大的数据进行分析。本文选取了第三台阶的信号。该信号和理想线性调频信号的相位如图4、图5所示。根据式(6),两者的相位差Δφ如图6所示。

图4 通道1内定标数据信号相位
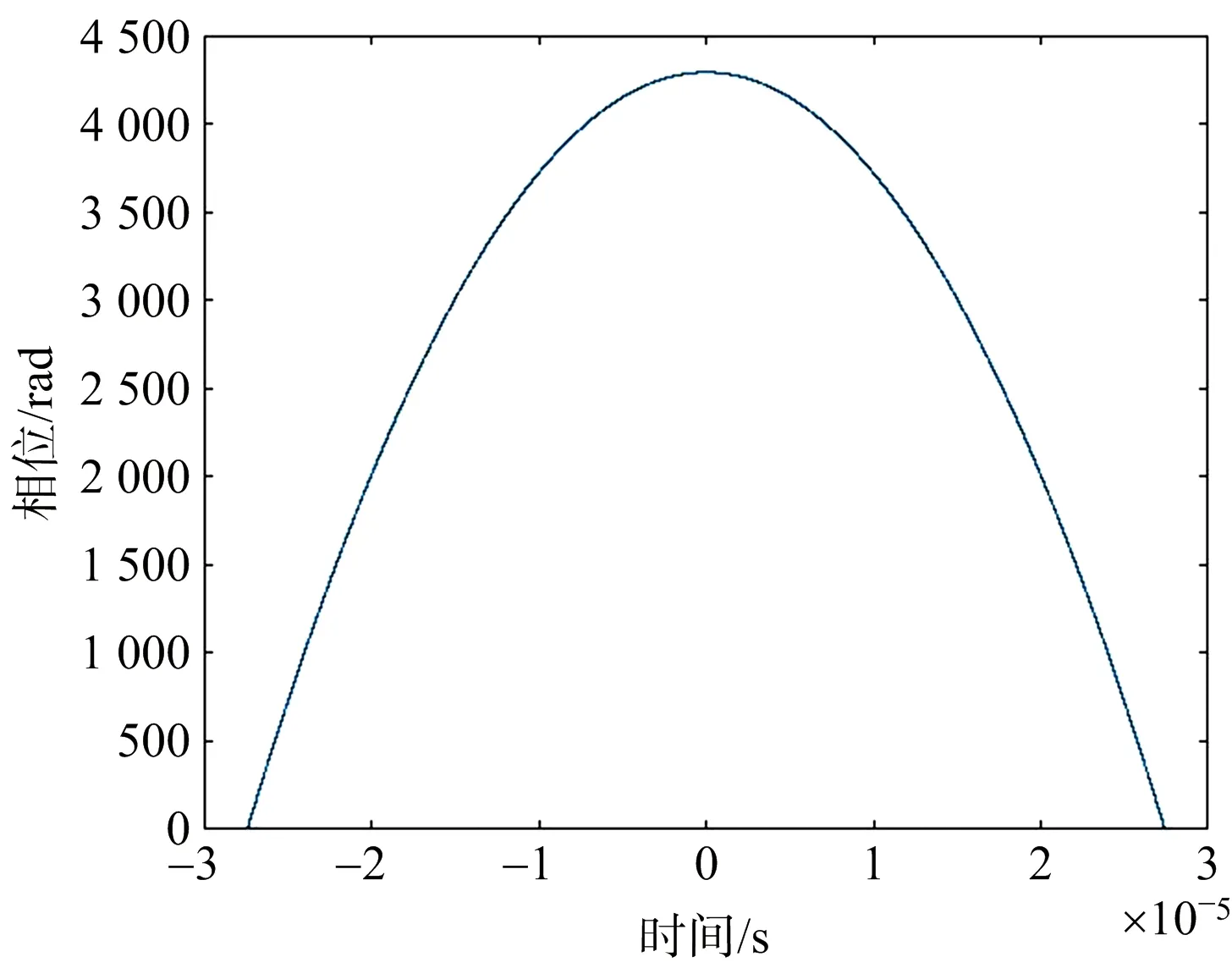
图5 理想线性调频信号相位
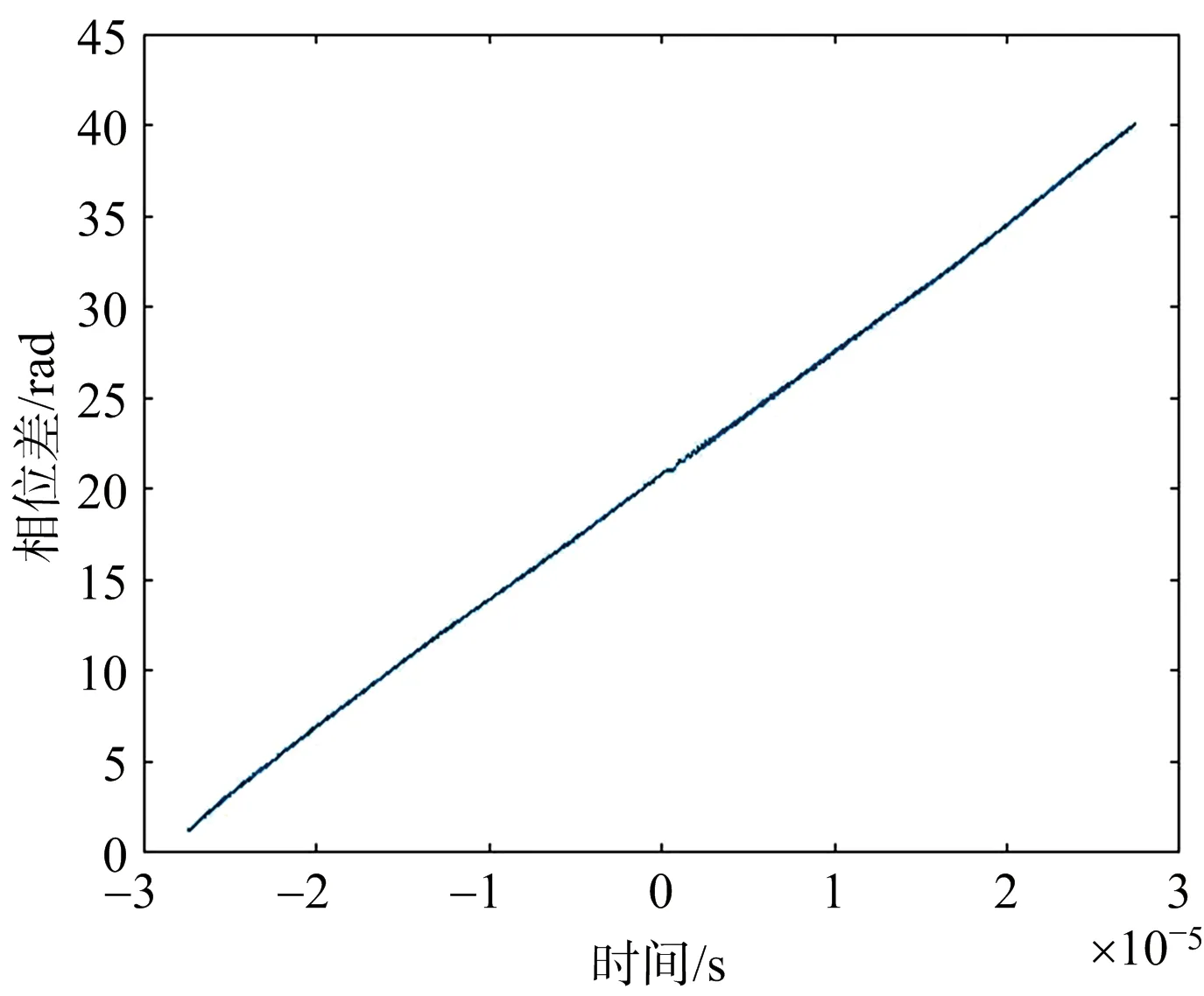
图6 通道1相位差Δφ
令k为上述直线的斜率。由式(6)可得
(8)
求出时延tm后,即可通过式(6)获得相位误差φm(t)。通道1相位误差如图7所示。
(9)
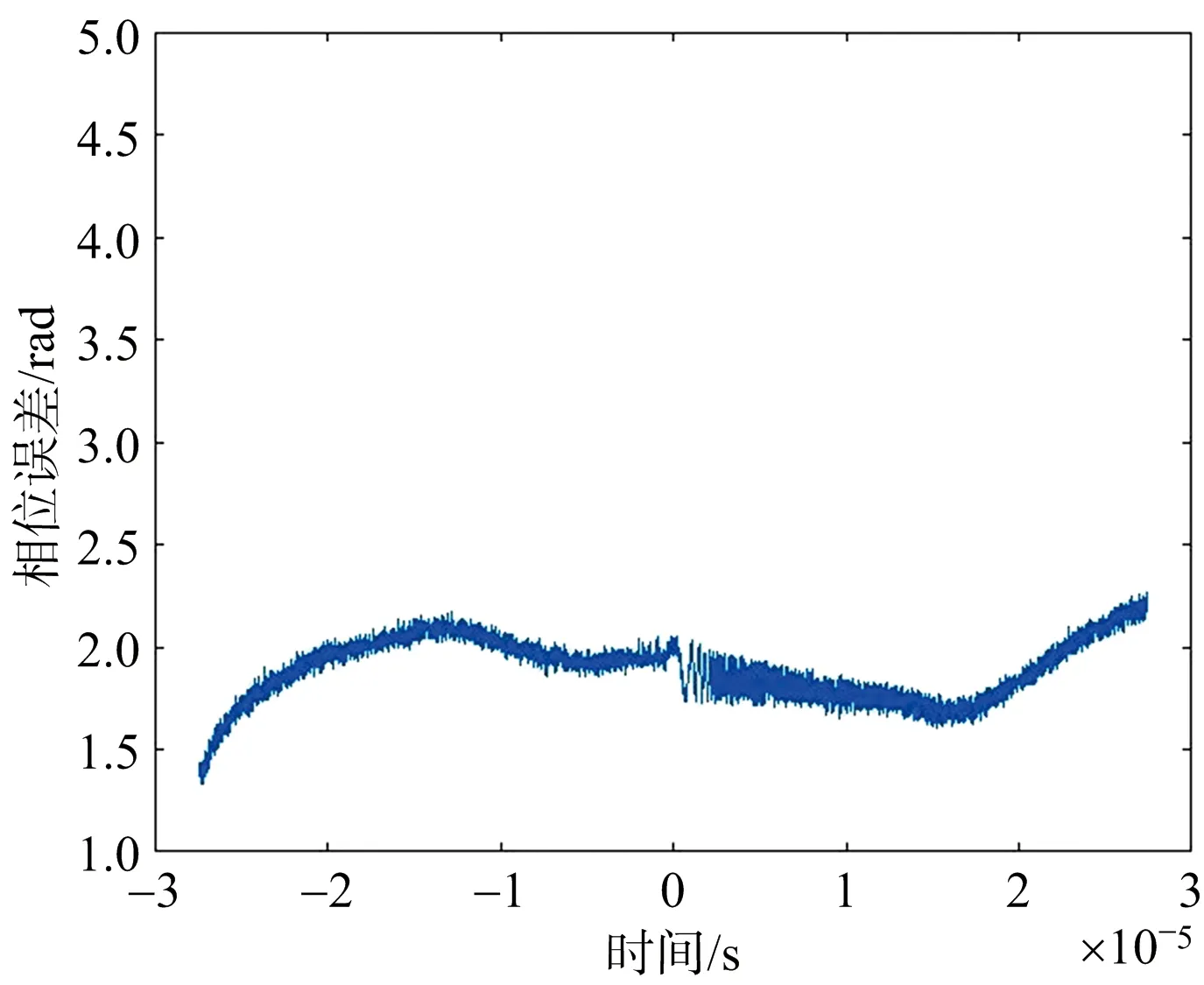
图7 通道1相位误差φm(t)
至此,可获得高分三号两个通道的时延和相位误差,按照第2节所述流程对回波数据进行补偿。图8、图9是两个通道内定标信号频域幅度图。以通道2作为基准,从图8和图9中估计出通道1和通道2的幅度比,然后对通道1回波数据进行补偿。
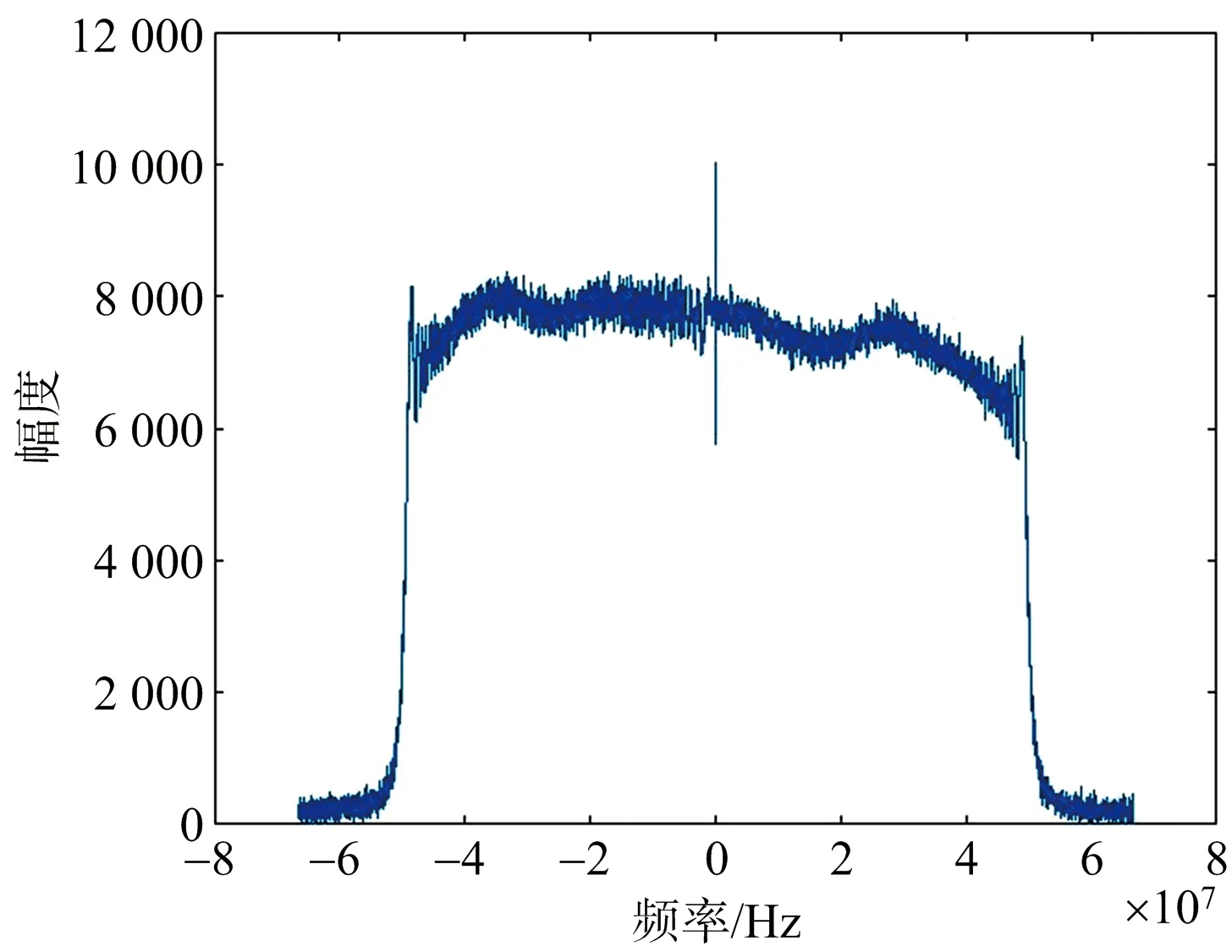
图8 通道1内定标信号频域幅度
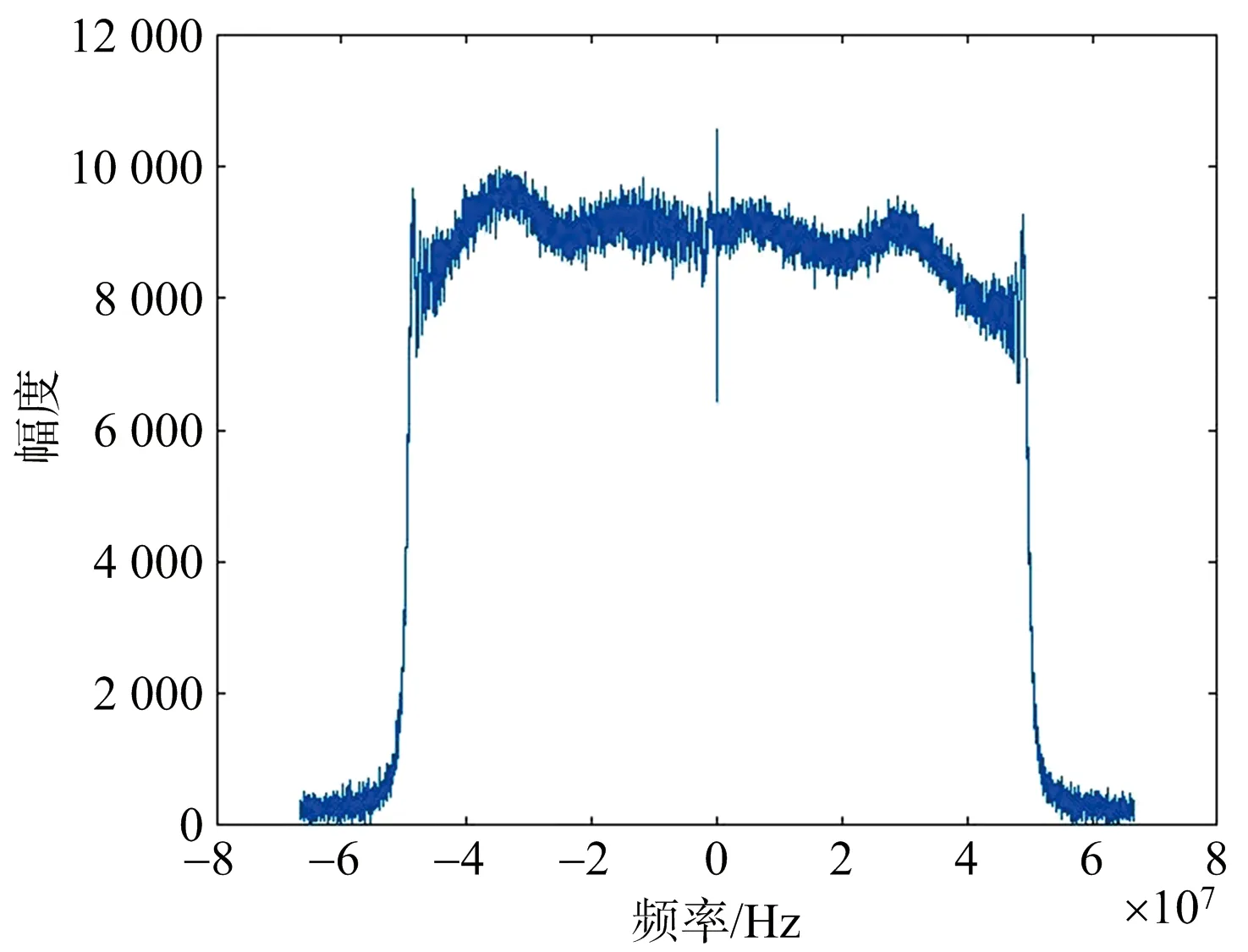
图9 通道2内定标信号频域幅度
采用本文算法处理高分三号实测数据,结果如图10所示。图11为未进行通道误差估计及补偿直接进行成像的结果。从图11可以看到,通道误差会导致虚假目标的存在,对图像质量造成严重影响。从图10可以看出,本文算法很好地抑制了方位模糊。其成像结果验证了算法的有效性。同时,运用正交子空间法[9]处理该数据,将其结果和文中算法处理结果进行对比。图12为运用正交子空间法估计误差并进行补偿后的结果。从图12可以看出,水陆交界处正交子空间法的效果不好,模糊依然存在。

图10 本文算法处理结果

图11 未校正图像

图12 正交子空间法处理结果
从图10和图12可见,在性能上,基于内定标数据的估计误差方法略优于正交子空间法。这是由于基于内定标数据的方法将各通道回波补偿为相同的较理想信号,而正交子空间法补偿的是通道间的固定相位偏差,各通道的幅频特性和相频特性仍存在一定差别,没有完全补偿。为了更清晰地看到成像结果,放大图10部分区域,如图13、图14所示。图13为山区地区,图14为河滩地区。从图13和图14可见,本文算法在不同地形区域处理效果良好,聚焦清晰。算法具备良好的鲁棒性。

图14 本文算法河滩处理结果
4 结束语
本文先通过内定标数据估计出通道延迟、相位误差、幅度误差,然后在距离频域对回波数据进行误差补偿。高分三号实测数据的处理结果验证了算法的有效性。除此,算法具有良好的鲁棒性,适用于不同地形区域。本文算法误差估计来源于内定标数据,较基于回波数据的误差估计方法,处理数据量小,适用于可以获取到内定标数据的情形。

