双干扰机InISAR微动调制干扰
唐峥钊,赵国庆
(西安电子科技大学电子工程学院, 陕西西安 710071)
0 引言
逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)具有对非合作机动目标的二维高分辨成像能力,同时也存在以下缺陷:首先,二维ISAR图像是目标在距离-多普勒平面上的投影图像,不包含目标各散射中心的高程信息;其次,二维ISAR图像多普勒维坐标不反映目标真实横向尺寸;此外,ISAR成像对象多为非合作机动目标,成像效果依赖于目标运动状态,目标二维ISAR图像可能随时间变化而显著不同,这对非合作目标识别造成一定困难。
干涉逆合成孔径雷达(Interferometric Inverse Synthetic Aperture Radar, InISAR)是将干涉技术与逆合成孔径成像技术相结合的高分辨三维成像雷达[1]。其基本思想是利用位置分布不同的多个天线获得具有一定视角差的多幅目标二维ISAR图像,再通过干涉相位处理[2],恢复出目标各散射中心的高程信息,从而得到目标真实三维分布[3]。相比与传统ISAR,InISAR可以获得远距离运动目标的三维结构及真实尺寸[4],且受目标姿态变化影响较小,为非合作目标识别提供了更加全面、稳定的信息,具有一定理论研究意义和工程应用价值。因此,开展针对InISAR的干扰技术研究也成为雷达电子对抗领域的一个热点和难点。
目前公开发表的文献资料中关于InISAR干扰技术的研究较少,对于干涉合成孔径雷达(InSAR) 干扰技术的研究也尚处于起步阶段。文献[5]提出了利用多部干扰机对单航过InSAR产生场景欺骗干扰的干扰方法。文献[6]研究了常规噪声调制干扰和弹射式干扰对InSAR成像的影响。文献[7]指出单个天线任意波形调制干扰最终干涉相位都近似为常数。文献[8]研究了通过双(多)干扰机的合理配置实现对InSAR三维欺骗干扰的可能性。
此前研究表明,单部干扰机所发射干扰信号在InISAR成像期间具有近似恒定的干涉相位,导致其无法对InISAR产生具有高程信息的干扰效果,针对这一问题本文提出了基于双干扰机的In- ISAR微动调制干扰方法。雷达目标的微多普勒效应指由于目标部件旋转、进动、振动等微运动[9]导致成像雷达二维距离-多普勒图像方位向扩展进而使成像质量下降的现象[10]。两部干扰机通过发射带有微动调制信息的干扰信号,可在InISAR天线各通道内形成等效于真实微动假目标回波信号的干涉相位图,从而产生具有高程信息的三维干扰效果。文中首先给出了InISAR成像原理,并在此基础上推导了干扰信号合成方法,最后通过仿真验证方法的有效性。
1 InISAR成像原理
InISAR系统通常采用具有正交基线的多天线构型,包括L型和十字型天线结构等,前者因结构简单、相干性好等优点被较多使用,其几何结构如图1所示。收发天线A分别与接收天线B、C构成两对互相垂直干涉基线,基线长度都为D。M、N分别为AB、AC基线中点。以基线方向为X、Z轴建立如图三维坐标系XYZA。目标点散射模型如图2所示,初始时刻目标散射中心O点坐标为(XO,YO,ZO),θ为OM与Y轴正向夹角,目标上任意一散射点P坐标为(XP,YP,ZP),O、P两点与三天线及M点间距离分别为RAO、RBO、RCO、ROM、RAP、RBP、RCP、RPM,目标速度矢量为V,以O为中心、与XYZA坐标轴平行方向建立目标本地三维坐标系xyzO。

图2 目标散射点模型
设天线A发射线性调频脉冲信号为
(1)

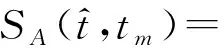
exp[j2π(fc(t-2RAP/c)+
(2)
设RrefA为参考距离,对式(2)进行dechirp处理得

(3)
在距离向作傅里叶变换,得一维距离像为
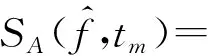
(4)
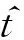
Tr为相干积累时间,将式(5)对慢时间作傅里叶变换可得二维ISAR距离-多普勒图像:
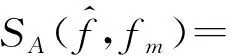
(6)
同理可得天线B接收回波经成像处理后的ISAR图像为

(7)
则可得P点处干涉相位为
(8)
式中,Angle(·)表示取复数值相位。InISAR成像过程中,通过对各天线接收回波的包络对齐及相位校正等运动补偿处理,目标可等效为远场转台模型,此时P点干涉相位可表示为
(9)
可得P点在AB基线方向坐标为
(10)
同理,利用AC两天线接收回波数据干涉处理可得P点在AC基线方向坐标为
(11)
在远场条件下,P点在Y轴坐标YP与斜距RAP近似相等,可通过测距获得。则经过以上步骤,可得P点三维空间坐标,实现了对该散射点的三维干涉成像。
2 单站干扰分析
采用如图1所示系统模型,假设单部干扰机位置坐标为J1(XJ1,YJ1,ZJ1),干扰机与天线距离分别为RJ1A(t),RJ1B(t),RJ1C(t)。则tm时刻干扰信号在AB天线通道内相位差为
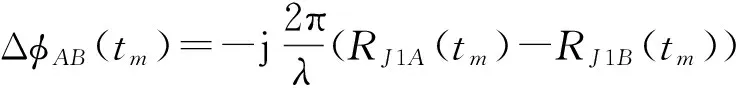
(12)
式中,
RJ1A(tm)-RJ1B(tm)=
(13)
将式(13)在XJ1处泰勒展开并忽略高次项得
(14)
由式(14)可知,由于InISAR成像期间XJ1近似不变,则单干扰机干涉相位近似为恒定值,因此无法对InISAR产生具有高程信息的干扰效果。
3 双站干扰信号产生
干扰信号产生流程如图3所示。
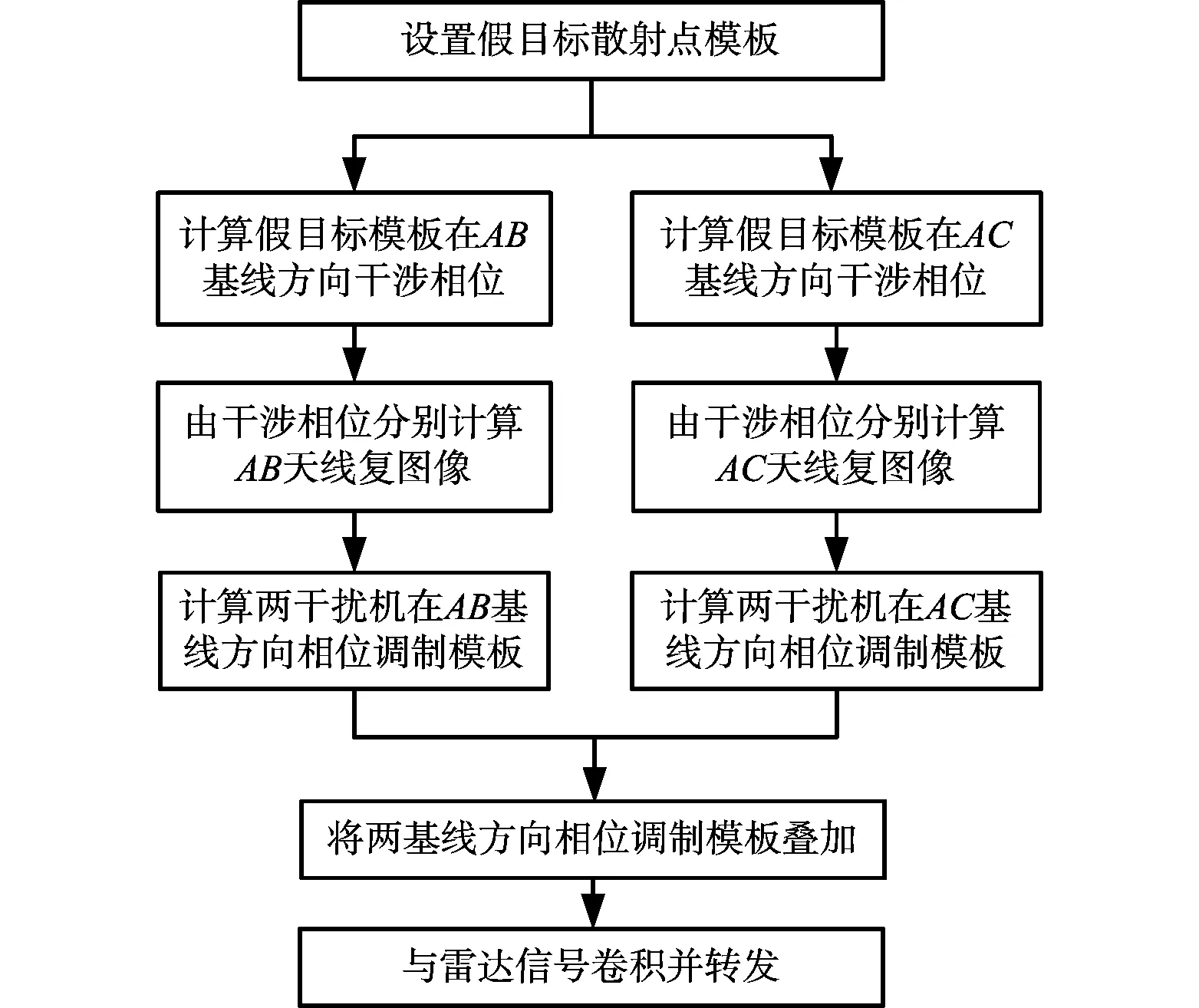
图3 干扰信号产生流程图
仍采用图1系统模型。设两干扰机位置坐标为J1(XJ1,YJ1,ZJ1),J2(XJ2,YJ2,ZJ2),两干扰机与天线距离分别为RJ1A,RJ1B,RJ1C,RJ2A,RJ2B,RJ2C。设假目标模板由N个散射点组成,各假目标点初始位置随机分布在O点周围半径RP范围内,且绕O点作角速度为ωP的圆周运动。
设第i个假目标点在tm时刻三维坐标为Pi(xi(tm),yi(tm),zi(tm)),与AB天线距离差为ΔRABPi(tm)。则由式(8)可得tm时刻假目标模板在AB天线对的干涉相位为
(15)
设两干扰机发射的干扰信号分别为J1和J2,两干扰信号在A,B天线聚焦后的复图像分别为SAJ1,SAJ2和SBJ1,SBJ2,A天线聚焦后复图像SA(x,y)可表示为两干扰信号复图像的叠加,即
SA(x,y)=SAJ1(x,y)+SAJ2(x,y)
(16)
设两干扰机自身在A、B天线对的干涉相位分别为ΔφABJ1和ΔφABJ2,由式(9)可知干涉相位由干扰机和天线相对位置决定,在本系统模型中为常数。
B天线复图像等效于由A天线复图像补偿假目标干涉相位得到,实际通过补偿两干扰机干涉相位后叠加得到,即
SA(x,y)exp(jΔφAB(tm))=
SAJ1(x,y)exp(jΔφABJ1)+
SAJ2(x,y)exp(jΔφABJ2)
(17)
由式(16)、式(17)可得
SAJ1(x,y)=SA(x,y)·
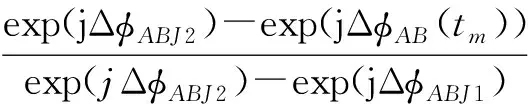
(18)
SAJ2(x,y)=SA(x,y)·
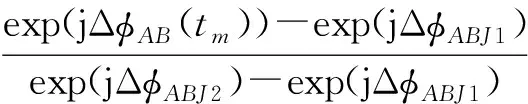
(19)
即当J1和J2在A天线聚焦后图像SAJ1(x,y)和SAJ2(x,y)满足式(18)、式(19)时,可在AB基线方向产生等效于假目标模板的干涉相位。
SA(x,y)等效于假目标模板在A天线成像效果,则由式(6)得其相位信息φA(tm)为
(20)
式中,RAi(tm)为tm时刻第i个假目标点到天线A的距离。SA(x,y)可表示为
(21)
式中,σi为第i个假目标点的散射系数。
由式(8)得两干扰机在AB天线对的干涉相位为
(22)
(23)
将式(15)、式(21~23)分别代入式(18)、式(19)可求得SAJ1,SAJ2。至此,将两干扰机在AB基线方向干扰问题转化为对天线A的两个二维干扰问题。根据传统欺骗调制干扰方法,可求得此时干扰信号相位模板,设为ΔφJ1AB(tm),ΔφJ2AB(tm)。
同理,可求得AC基线方向,两干扰信号应满足的调制相位模板,记为ΔφJ1AC(tm),ΔφJ2AC(tm)。
由于AB、AC两基线方向垂直,干扰信号在某一基线方向产生的高程信息在另一基线方向表现为同一分辨单元内,可相互叠加,则可得两干扰机实时调制相位模板为
φJ1(tm)=ΔφJ1AB(tm)+ΔφJ1AC(tm)
(24)
φJ2(tm)=ΔφJ2AB(tm)+ΔφJ2AC(tm)
(25)
最后将干扰信号与截获的雷达信号卷积并转发可得到三维微动调制干扰效果。
4 仿真及结果分析
本仿真采用如图1所示场景,目标点散射模型如图2所示。以天线A为坐标原点,基线长度为10 m,目标散射中心坐标为O(50 km,20 km,10 km)。目标在XOY及XOZ平面内正向旋转角速度均为0.02 rad/s,雷达信号载频为10 GHz,带宽为200 MHz,脉宽为10 μs,重频为200 Hz,脉冲积累个数为512个,干扰机采样率为480 MHz。
图4为无干扰时InISAR成像效果图。图5为附加单部干扰机射频噪声干扰的目标InISAR图像,由图5可以看出单部干扰机的干扰效果具有恒定的高程信息,无法有效对InISAR图像造成影响。
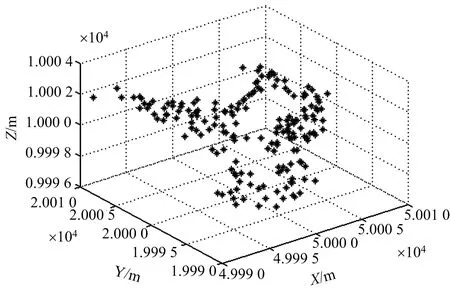
图4 无干扰时InISAR图像
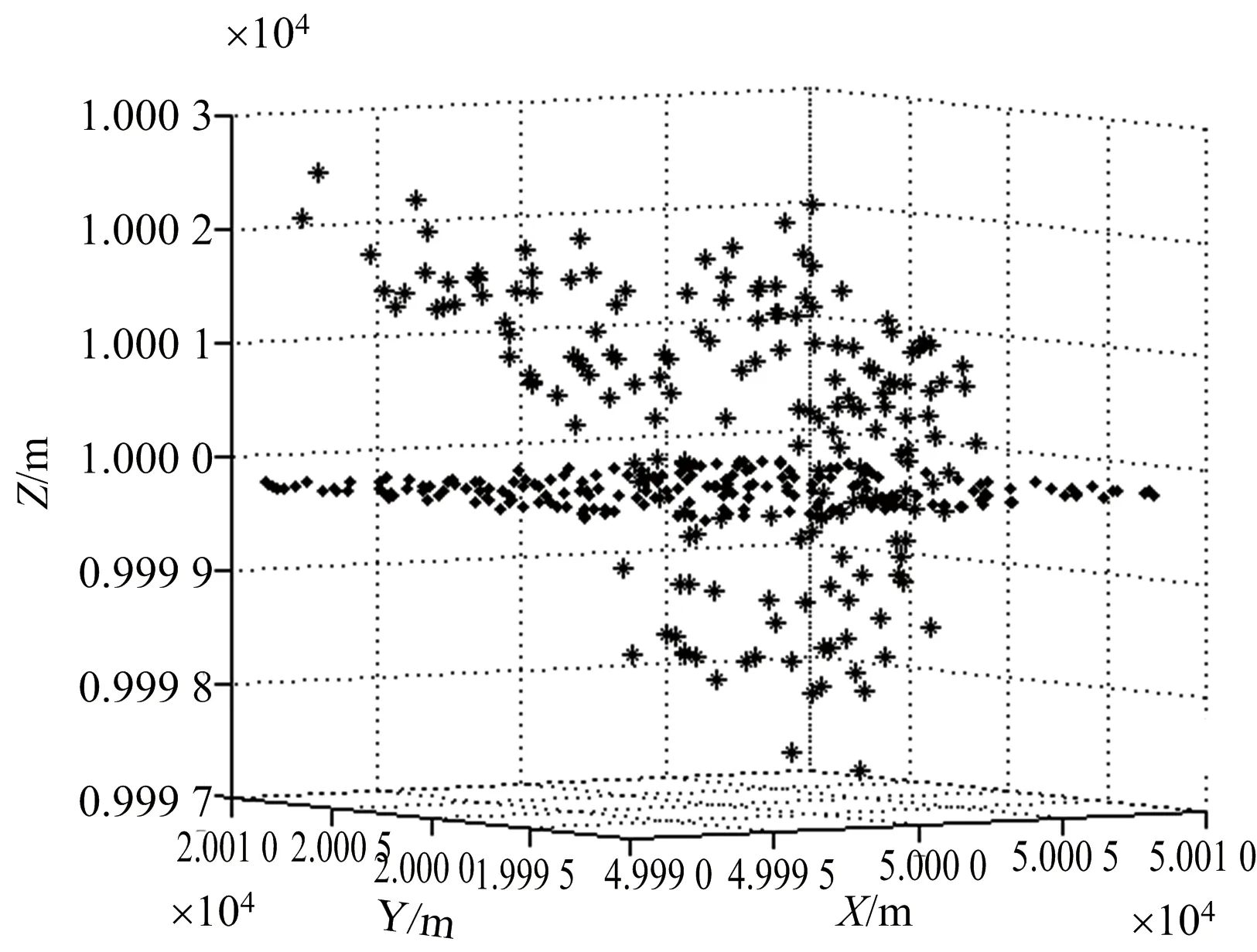
图5 单干扰机射频噪声干扰
图6为双干扰机微动调制干扰效果图。设存在10个旋转微动假目标点,其初始位置随机分布在目标散射中心周围半径rp内,同时各假目标点绕目标散射中心以角速度10 rad/s进行圆周运动。图6(a)和图6(b)分别为rp为0.8 m和3 m的干扰效果。可以看出,旋转微动假目标点可在InISAR图像中产生具有高程信息的干扰条带,且干扰条带高程范围与假目标点运动范围一致。根据需要设置假目标点运动模型,可分别达到部分遮盖和完全遮盖真实目标InISAR图像的效果,对InISAR目标识别及特征信息提取造成一定影响,达到三维干扰的目的。
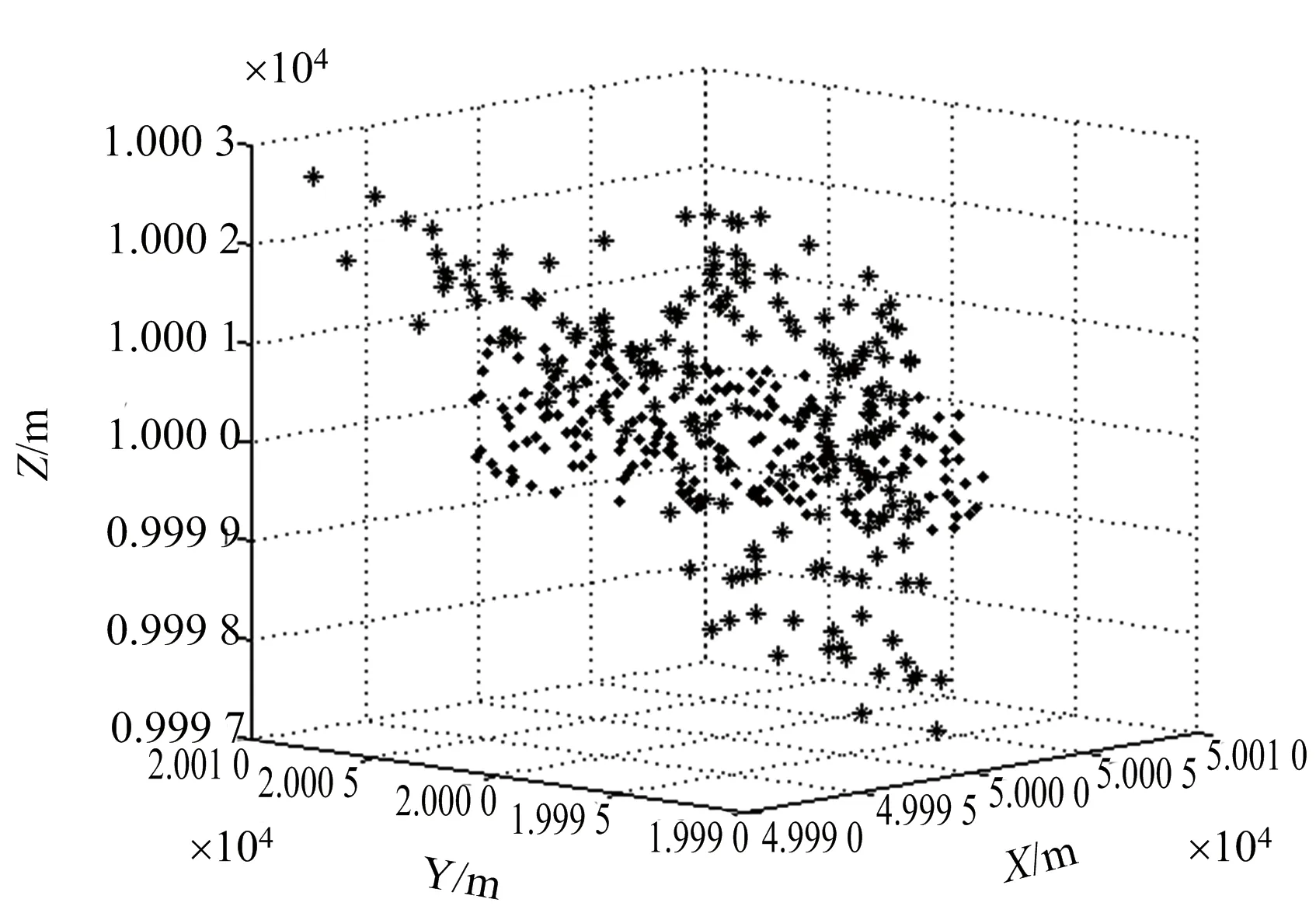
(a) rp=0.8 m
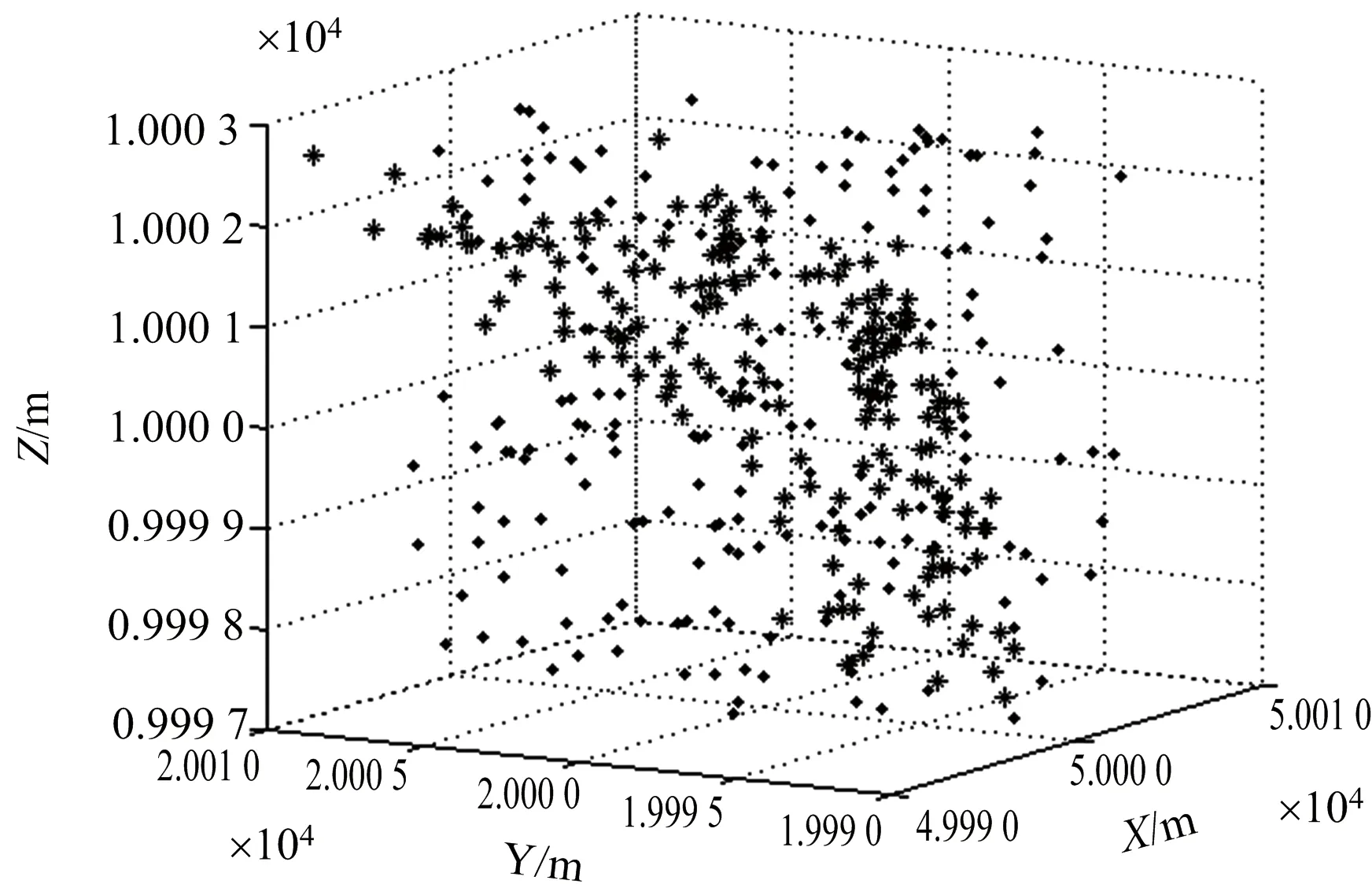
(b) rp=3 m图6 双干扰机微动干扰
5 结束语
本文研究了双干扰机的InISAR微动调制干扰方法。根据旋转微动假目标散射点模板,两部干扰机分别发射具有特定相位关系的干扰信号,干扰信号在InISAR收发天线通道内叠加,可产生等效于微动假目标散射点回波的干涉相位,经过成像处理后可产生具有高程信息的干扰条带,且干扰条带范围可根据假目标模板变化,从而达到对InISAR的三维干扰效果。

