双轴连续旋转调制捷联惯导系统大失准角初始对准技术
许昊天,赵春柳,邵海俊,缪玲娟
(1.北京理工大学自动化学院,北京100081;2.国家国防科技工业局军工项目审核中心,北京100039)
0 引言
由于隐蔽性好、自主性强,捷联惯导系统(Strapdown Inertial Navigation System,SINS)可在各种复杂环境下工作,已成为了一种被广泛应用的系统[1⁃2]。由于SINS的导航误差会随时间增加而积累,因此SINS在长时间条件下的导航精度会有所降低。目前,许多先进的SINS均采用了旋转调制技术来补偿惯性器件的输出误差[3]。为了解决单轴旋转调制技术无法调制旋转轴方向上器件误差的问题,许多学者对双轴旋转调制技术展开了研究[4⁃5]。
初始对准是惯性导航的核心技术之一,其对准精度直接决定了后续导航的精度[6⁃7]。在SINS初始对准的研究中,通常将误差模型看作经典的线性模型,这种线性模型是在惯导系统粗对准后姿态误差角较小的情况下获得的。在工程实际中,由于基座晃动及各种干扰的存在,粗对准后的姿态误差角并非小角度,基于小失准角的线性误差模型无法满足现实应用的要求,基于大失准角捷联惯导系统的误差模型和非线性估计方法得到了许多学者的关注[8⁃9]。
近年来,平方根容积Kalman滤波算法(Square⁃root Cubature Kalman Filter,SCKF)已可以很好地解决SINS大失准角初始对准问题,但其需要对噪声的统计特性有准确了解,否则可能出现很大的状态估计误差,甚至导致滤波发散[10]。Sage⁃Husa算法能够实时在线估计系统的噪声统计特性,从而显著提高滤波算法的自适应能力[11⁃13],但其只能被应用于线性系统中。因此,本文将SCKF算法与Sage⁃Husa算法相结合,提出了采用QR分解来完成对噪声协方差的平方根矩阵进行估计的ASCKF算法,从而提高了非线性滤波算法的自适应性,同时避免了传统Sage⁃Husa SCKF算法在非线性较强的情况下易出现系统过程噪声协方差矩阵与量测噪声协方差矩阵不正定的情况。
1 坐标系定义
以下为本文所涉及到的坐标系:
(1)地心惯性坐标系(i系)
原点选为地心,zi轴沿地球自转方向,xi轴、yi轴位于赤道平面内,xi轴从地心指向春分点,yi轴与xi轴、zi轴构成右手坐标系。
(2)地球坐标系(e 系)
原点位于地心,ze轴沿地球自转方向,xe轴指向赤道平面与格林尼治经线的交点,ye轴与 xe轴、ze轴构成右手坐标系。
(3)地理坐标系(t系)
原点位于载体的质心处,xt、yt、zt分别指向东向、北向、天向。
(4)导航坐标系(n 系)
本文选取地理坐标系为导航坐标系。
(5)载体坐标系(b 系)
与载体固连,其原点位于载体重心,xb轴、yb轴、zb轴分别指向载体的右、前、上方向。
(6)惯性测量单元坐标系(s系)
原点位于惯性测量单元(IMU)的重心,3个坐标轴的指向为惯性传感器的敏感轴,初始时刻s系坐标轴指向与b系一致。对于单轴旋转式惯导系统而言,转动方向为绕方位轴旋转;对于双轴旋转式惯导系统而言,转动方向为绕方位轴和横滚轴旋转。
2 旋转调制机理及误差分析
旋转式SINS采用传统SINS的解算算法对惯性测量单元的输出信息进行导航解算,从而得到导航结果。导航解算过程如图1所示。
旋转式SINS的基本工作原理与传统SINS一致,只是在SINS的基础上添加了旋转平台。旋转式SINS的位置误差方程与传统SINS一致,在此不再列出。其姿态和速度误差模型为

图1 导航解算方案Fig.1 Scheme of navigation solution

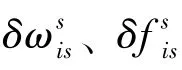
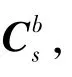
假设在任意时刻t,IMU绕任意旋转轴的旋转角度为α(t),则s系到b系的变换阵为


图2 b系与单轴旋转s系之间的关系Fig.2 Relationship between b-system and uniaxial rotation s-system
在旋转式捷联惯导系统中,惯性器件安装于平台上,测量的是s系相对于i系的运动。因此,惯性器件的信号输出可以表示为
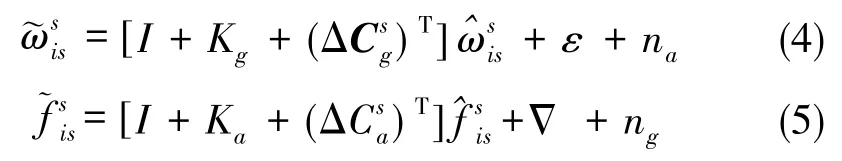
忽略二阶及二阶以上小量,由式(4)、式(5)可以推出,陀螺和加速度计的输出误差为

当系统进行旋转调制时,与旋转轴垂直的两个轴上的惯性器件误差会被调制为正余弦形式,而在旋转轴方向上的误差则不被调制。将式(8)、式(9)在一个旋转周期内进行积分,由于与旋转轴垂直方向的误差是正余弦形式,因此其积分结果为0,从而可抑制系统误差,而在旋转轴方向上的误差则按照原来的规律传播。因此,单轴旋转式捷联惯导系统只能抑制与旋转轴相垂直的两个轴向上的误差,而无法减少旋转轴上的误差。若想抑制三个轴上的误差,可采用双轴旋转调制方案。
3 双轴旋转调制方案设计
本文采用十六次序双轴连续旋转方案,具体转位方案与文献[14]相同。
设惯性测量单元的旋转速率为Ω,次序1、3、6、8绕方位轴转动,在载体坐标系O⁃xbyb平面内呈现出正、反一周的变化规律。设每一次序转动时间为T/2,则在转动过程中陀螺常值漂移在载体坐标系x轴的投影积分为

由式(10)和式(11)可知,次序 1、3、6、8 在转动过程中累积的常值误差为0,即

根据类似的计算方式,次序2、4、5、7绕横滚轴转动,在转动过程中在载体坐标系O⁃xbzb平面内同样呈现出正、反一周的变化规律,累积的常值误差为0,即
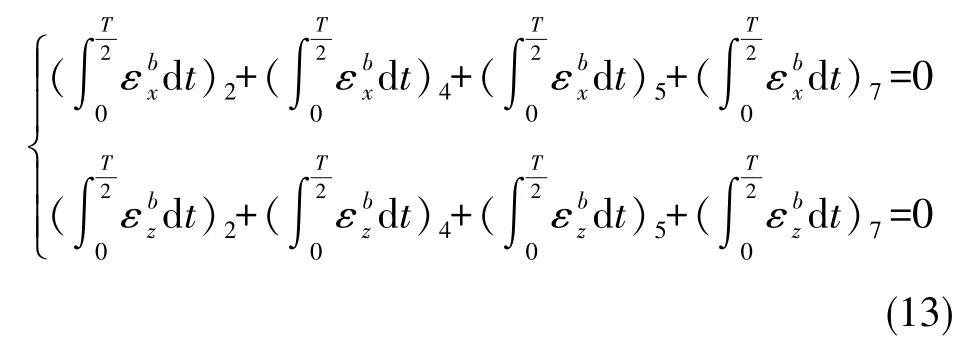
次序9、11、14、16绕方位轴转动,在转动过程中在载体坐标系O⁃xbyb平面内呈现出正、反一周的变化规律,累积的常值误差为0,即

次序10、12、13、15绕横滚轴转动,在转动过程中在载体坐标系O⁃xbzb平面内呈现出正、反一周的变化规律,累积的常值误差为0,即
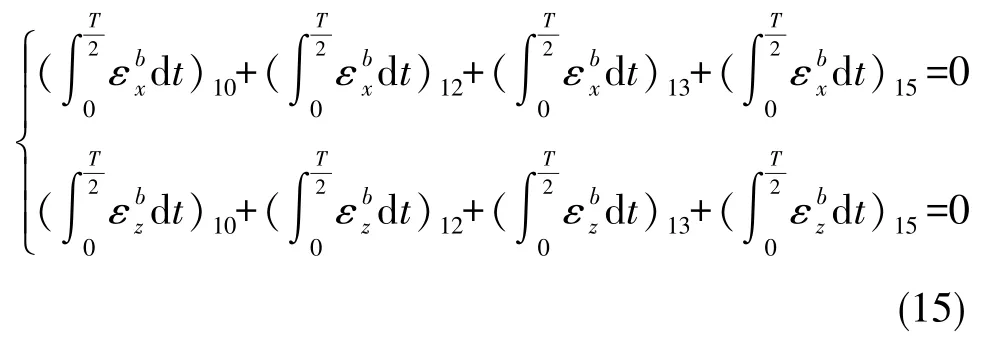
由式(10)~式(15)可知,陀螺的常值漂移被完全调制。加速度计的常值偏值调制过程与陀螺类似,因此本文选择的十六次序双轴连续旋转方案可将惯性器件的常值误差完全调制,进而避免了误差的积累。
文献[14]表明,在采用十六次序双轴旋转调制方案后,惯性器件标度因数误差的影响与传统SINS一致,标度因数误差不会引起导航坐标系下东向角误差,但会由于标度因数误差与地球自转角速度分量耦合而引起北向和天向角误差,并随时间积累。安装误差会与地球自转角速度分量耦合引起随时间积累的姿态角误差,本文限于篇幅不再对这两项误差进行计算。
4 ASCKF算法
4.1 非线性误差模型
在静基座初始对准中,由于在实际的工程环境中存在基座晃动及各种干扰,粗对准后的姿态误差角比较大,此时无法使用传统的线性滤波方程进行精对准。严恭敏[9]针对这一问题研究了捷联惯导系统非线性误差模型,设导航坐标系(n系)经历三次转动到达计算导航坐标系(n′系),三次转动的角度分别为 αx,αy,αz。令 α=[αxαyαz]T,有



该状态方程和量测方程为惯导系统误差模型的通用表达式,后文运用该表达式进行了滤波对准。
4.2 SCKF算法
平方根容积Kalman滤波算法(SCKF)由于滤波精度高、稳定性强,在非线性系统中的应用较为广泛。因此,本文选择该算法在静基座条件下进行初始对准。
设非线性系统离散化的状态方程与量测方程为

式(18)中,f为非线性状态转移矩阵,h为线性量测矩阵,wk-1、vk为互不相关的零均值Gauss白噪声,方差分别为Qk-1、Rk。SCKF算法的计算步骤如下所示:
(1)初始化,给定均值和协方差

计算球容积点和权值,即有
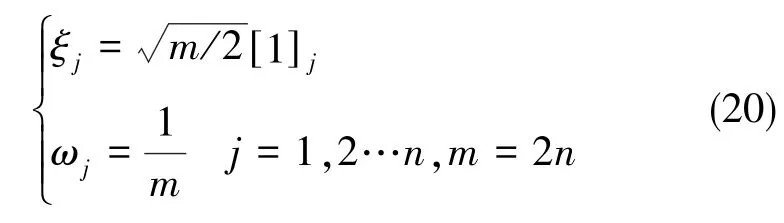
式(20)中,[1]=[I,-I],I为 n 维单位方阵,[1]j表示取[1]的第 j列。
(2)时间更新

SCKF算法借鉴了平方根滤波的思想,避免了复杂的矩阵求逆和分解运算,直接以协方差平方根矩阵的形式在相邻时刻间进行递推更新,能够有效提高滤波的计算效率和数值稳定性。
4.3 传统的Sage-Husa SCKF算法
SCKF算法在用于大失准角初始对准时需要对噪声的统计特性有准确了解,否则可能出现很大的状态估计误差,甚至导致滤波发散。王思思[10]提出的Sage⁃Husa SCKF算法利用Sage⁃Husa噪声估计器对系统噪声的均值qk及观测噪声的均值rk进行了在线估计,并对系统过程噪声协方差矩阵Qk、观测噪声方差矩阵Rk进行了实时修正,从而使得SCKF算法具有了自适应性。
假设非线性系统中的时变噪声wk、vk分别为互不相关的Gauss白噪声,过程噪声的协方差Qk为非负定矩阵,量测噪声的协方差Rk为正定矩阵。在估计时变噪声的统计特性时,应当注重最新数据对系统的影响,逐渐遗忘陈旧数据。传统的Sage⁃Husa SCKF算法可总结如下:
(1)初始化
按照式(19)、式(20)完成参数初始化过程,并对Q0、R0、q0、r0赋予初始值。
(2)状态估计
按照式(21)~式(38)进行 SCKF 滤波估计。
(3)噪声参数估计
按照式(39)~式(42)对噪声参数进行更新。
系统过程噪声的均值为

通过在SCKF中加入Sage⁃Husa时变噪声统计估计器,可以有效估计出当前时刻的系统过程噪声与量测噪声,减少陈旧数据对滤波过程的干扰,从而提高滤波算法的自适应性。
4.4 ASCKF算法
由于传统的Sage⁃Husa SCKF算法在系统阶次较高或系统非线性较强的情况下易出现系统过程噪声协方差矩阵Qk与量测噪声协方差矩阵Rk不正定的情况,进而易导致滤波算法无法继续进行计算。因此,本文提出了改进Sage⁃Husa SCKF算法,即AS⁃CKF算法。该算法利用QR分解来完成对噪声协方差平方根矩阵的估计,避免了传统Sage⁃Husa SCKF算法在非线性较强的情况下易出现系统过程噪声协方差矩阵与量测噪声协方差矩阵不正定的情况,从而可配合SCKF算法完成自适应滤波过程。
针对式(18)所描述的系统,本文提出的ASCKF算法的具体过程如下所示:
1)设定初值,并设定 SQ,0=chol(Q0)、SR,0=chol(R0)。其中,chol为矩阵的 Cholesky 分解。
2)按照式(21)~式(38)进行 SCKF 滤波估计。
3)对噪声统计特性进行估计。
观测噪声协方差的平方根为

系统过程噪声协方差的平方根为

将改进的 ASCKF 算法通过式(43)、式(44)计算噪声协方差的平方根矩阵,并直接将式(43)、式(44)分别带入式(31)、式(25)中,从而避免了传统 Sage⁃Husa SCKF 算法使用式(41)、式(42)进行计算时易出现的矩阵非正定问题,以及由此导致的式(27)、式(33)无法进行计算的问题。在下文的仿真分析中,将运用ASCKF滤波算法对双轴旋转式捷联惯导系统进行非线性初始精对准。
5 仿真结果与分析
5.1 SINS与旋转式SINS初始对准结果对比
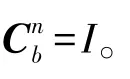
双轴旋转式SINS静基座的初始对准结果如图3所示,单轴旋转式SINS静基座的初始对准结果如图4所示,传统SINS静基座的初始对准结果如图5所示。
分别对三种惯导系统的初始对准结果进行20次Monte Carlo仿真实验,取各次实验的姿态角误差的算数平均值作为对准精度的评价指标,其结果如下:
1)双轴旋转式SINS的方位角误差为0.177°,俯仰角误差为0.006°,横滚角误差为-0.012°;
2)单轴旋转式SINS的方位角误差为0.219°,俯仰角误差为0.011°,横滚角误差为-0.014°;3)SINS的方位角误差为 0.374°,俯仰角误差为0.016°,横滚角误差为-0.019°。
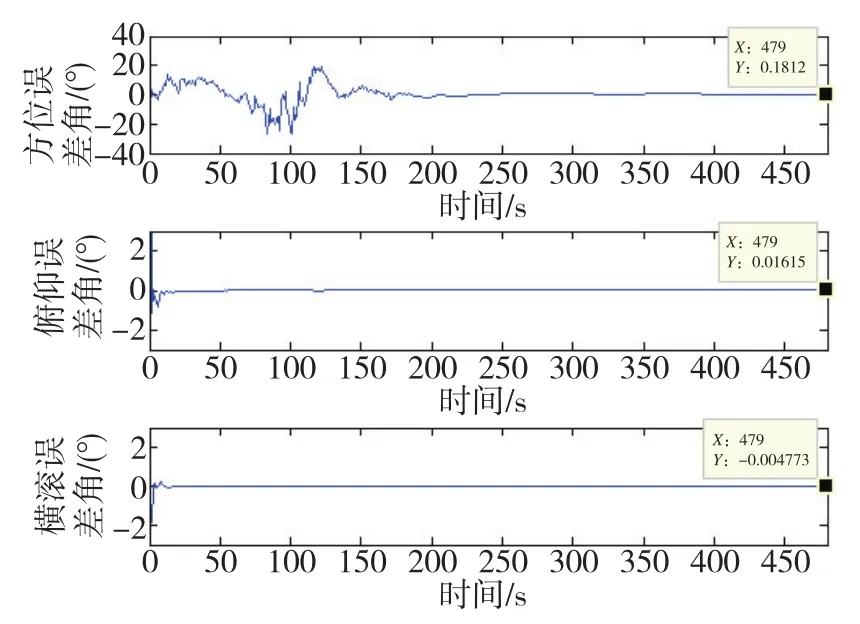
图3 双轴旋转式捷联惯导系统SCKF算法的初始对准结果Fig.3 Initial alignment of SCKF algorithm for biaxial rotary SINS
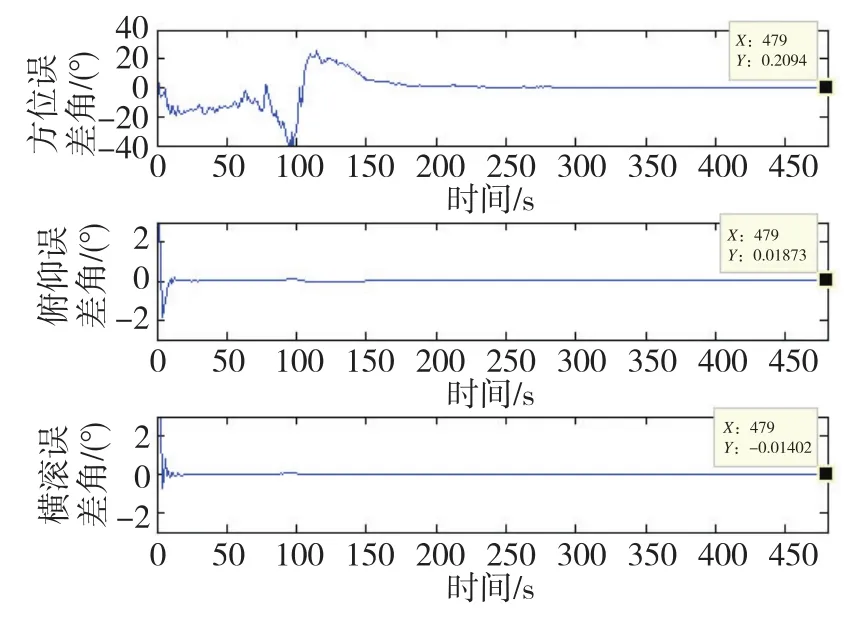
图4 单轴旋转式捷联惯导系统SCKF算法的初始对准结果Fig.4 Initial alignment of SCKF algorithm for single axis rotary SINS

图5 捷联惯导系统SCKF算法的初始对准结果Fig.5 Initial alignment of SCKF algorithm for SINS
显然,单轴旋转式SINS静基座的初始对准精度与双轴旋转式SINS基本相当。但由于对准时间有限,并且考虑到系统非线性对误差收敛速度的影响,单轴、双轴旋转式捷联惯导系统均未能让方位误差角收敛到一个较小的范围。传统SINS静基座初始对准精度不如两种旋转式SINS。
5.2 ASCKF算法的仿真结果与分析
为了验证在噪声模型不确定情况下的ASCKF滤波算法具有良好的自适应能力,本节采用十六次序双轴连续旋转方案,并通过实验模拟了噪声发生突变的情况。实验仿真的初始条件在5.1节的基础上,在300s后观测噪声的方差增大了100倍。采用SCKF滤波算法的静基座初始对准结果如图6所示,采用ASCKF滤波算法的静基座初始对准结果如图7所示。
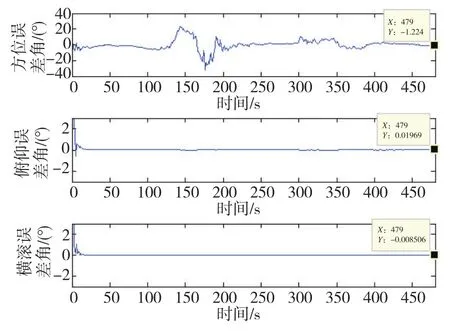
图6 双轴旋转式SINS SCKF滤波算法在噪声变化环境下的初始对准结果Fig.6 Initial alignment of biaxial rotary SINS SCKF algorithm in noisy changing environment

图7 双轴旋转式SINS ASCKF滤波算法在噪声变化环境下的初始对准Fig.7 Initial alignment of biaxial rotary SINS ASCKF algorithm in noisy changing environment
分别对两种滤波方案进行20次Monte Carlo仿真实验,取各次实验的姿态角误差的算数平均值作为对准精度的评价指标,结果如下:
1)双轴旋转式SINS采用SCKF算法在噪声统计特性发生突变的情况下进行大失准角初始对准的方位角误差均值为-1.528°,俯仰角误差均值为0.016°,横滚角误差均值为-0.018°。
2)双轴旋转式SINS采用ASCKF算法在噪声统计特性发生突变的情况下进行大失准角初始对准的方位角误差均值为0.307°,俯仰角误差均值为0.011°,横滚角误差均值为-0.015°。
显然,在噪声模型发生变化的情况下,采用传统的SCKF滤波方法会使方位角的对准精度明显降低,而ASCKF算法则具有很好的自适应性,可以很好地被应用于噪
6 结论
本文采用通过理论推导更好地抑制旋惯导系统的非SCKF算法,并法的基础上,提出了一种ASCKF滤波算法。该算法采用QR分解来完成对噪声协方差的平方根矩阵的估计,从而避免了传统Sage⁃Husa SCKF算法所面临的所估噪声协方差矩阵非正定所带来的问题。最后,通过仿真验证了在观测噪声发生突变的情况下ASCKF滤波算法具有良好的自适应性。

