基于数学核心素养理念的概念教学研究
吴晗 孙洪波
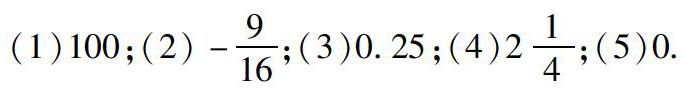

【摘要】数学核心素养是一种具有数学特征、使人具备良好的数学品格、适应社会发展的能力,对人综合素质提升至关重要.而数学概念课是所有数学教师必须直面的教学难题,本文在数学核心素养理念下,以“平方根”为例,阐述了如何进行概念教学.
【关键词】数学;核心素养;概念教学;平方根
素养是指一个人的综合素质,是人在思想、理论、知识、艺术等方面所达到的一定水平[1].数学素养是一个人经过数学学习后,除去所学到的数学知识外所留下的一种思维习惯与综合能力.具有数学素养的人会用数学的眼光看待世界,并善于把数学中的概念、结论和处理方法推广应用于认识一切客观事物上,在认识世界和改造世界的活动中,会充分体现数学的价值所在[2].《义务教育数学课程标准(2011年版)》明确提出了十个数学核心素养,包括:数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识[3].数学核心素养基于但又高于数学基本知识与技能,对于理解数学学科本质,设计数学教学,以及开展数学评价等有着重要的意义与价值,是数学的教学过程中应当特别关注的基本素养.
概念课是数学新授课当中教学难度最大的课型.数学概念是数学基础知识的重要组成部分,是判断和推理的起点,也是导出数学定理、法则等的逻辑基础[4].数学概念教学是数学基础知识和基本技能教学的核心,是发展数学思维、培养数学能力的重要途径.
因此,如何在数学学科核心素养理念下进行数学概念课教学,是所有数学教师必须直面的教学难题,也是值得大家认真思索研究的重要课题.下面,笔者以八年级华师版数学教材第11章第一课时“平方根”为例进行阐述.
教学过程:
1.引课:
问题一:边长为3 cm的正方形面积是多少?
问题二:面积为9 cm2的正方形边长是多少?
由3到9是乘方运算中的平方运算,而由9到3是一种什么运算呢?这种运算又有什么性质呢?
【设计意图】
(1)本节内容以实际问题开头,让学生体会数学知识来源于生活,并应用于生活.数学概念是抽象的,为了使学生更容易理解和接受,教学时要注意概念引入的途径和方式.教师根据学生的年龄特点、认知水平出发,可由日常生活或生产实际的材料引入,先感知,再理解.先抓住概念的本质特征,再引用实例,揭示对概念的本质属性的理解.
(2)两个问题很简单,但能让学生意识到一种互逆关系,为后面平方与开平方互为逆运算埋下伏笔.
(3)接下来的两个追问激发学生求知欲望,提高本堂课的学习兴趣.
2.概括平方根定义:
之前两个问题都利用了算式32=9,上标表明了一种运算,在这个运算下,3与9有着一定关系.9是3的平方,英文叫做“square”,那3是9的什么呢?英文叫做“square root”.square是“平方”的意思,而root有“根源、起因”的意思,我们把它叫做“平方根”.
再比如,52=25,5是25的平方根;
(-4)2=16,-4是16的平方根;
接下来请学生仿照老师再举几个例子,然后让学生试着说一说平方根的定义.
【设计意图】
(1)在算式32=9中了解3与9的名称,可以揭示二者的对应关系.
(2)英文“square root”能更好地诠释“平方根”名字的由来,促进学生对概念的理解.
(3)老师举的例子中平方根有正有负,让学生明白平方根不一定总是正数.
(4)學生仿照老师大量举例,可培养学生的数感与运算能力,帮助学生揭示概念的抽象过程,构建数学概念,生成数学知识.
3.巩固平方根定义:
例1 判断:
(1)2是4的平方根;
(2)-2是-4的平方根;
(3)9是3的平方根;
(4)0是0的平方根.
请同学们模仿这个句式举出正确的例子,最后总结:m是m2的平方根.
【设计意图】
(1)4个判断题和学生举例,引导学生对概念进行深入的剖析,紧扣概念本质,加深、巩固学生对平方根概念的理解与认知,掌握概念的内涵,突出教学重点.
(2)这个环节的举例,与上一环节类似,培养数感与运算能力.最后总结m是m2的平方根,使学生明白任何数都可以是某一个数的平方根.
4.平方根性质探索:
将之前的判断调过来说,对吗?
(1)4的平方根是2;(4的平方根除了2之外还有没有其他?有,-2.除了±2,还有没有了?是不存在,还是知识受限,暂时找不到了?)
(2)-4的平方根是-2;
(3)3的平方根是9;
(4)0的平方根是0.
判断并修改后,请学生模仿这个句式举出正确的例子,最后学生总结哪些数有平方根,以及它们的平方根有什么特点.老师梳理、总结.
【设计意图】
(1)4道小题,使学生感受到正数、负数、0的平方根的特点,认识到平方根的多样性.
(2)学生举例,体会平方根性质和求平方根的过程,为顺利总结出平方根性质做好准备.
(3)平方根性质的探索,其实是对平方根概念外延的一个探索过程,这能帮助学生更好的理解平方根的定义.
5.巩固平方根性质:
例2 下列各数是否有平方根?如果有,请求出它的平方根.
(1)100;(2)-916;(3)0.25;(4)214;(5)0.
【设计意图】
(1)不断应用、巩固平方根性质,多问“为什么”,使学生答题有据可依,夯实本节重点内容.
(2)本例题求平方根使开平方定义的出现水到渠成.
6.开平方、算术平方根概念及平方根的符号表示:
例2中,我们在求非负数的平方根,像这样的运算叫做开平方.我们能够体会到平方与开平方互为逆运算,我们可以借助平方来进行开平方.
对于一个正数a来讲,开平方的关键是找到它的正的平方根,我们把它叫做算术平方根,记作a.那么a的负的平方根怎么表示呢?
规定:0的算术平方根是0,记作0=0.那么-0有意义吗?
有了这样的理解,非负数a的平方根就是a和-a,合在一起记作±a,其中a称为被开方数.这个根号经历了相当漫长的演变过程,直到三百多年前,法国数学家笛卡尔用这个根号表示平方根,后来一直沿用至今.
【设计意图】
(1)开平方和算术平方根两个概念都依托平方根定义得来,所以这里直接给出.
(2)算术平方根定义是针对正数说的,对于0有一个单独的规定,二者在符号给出后都追问了相反数的表达形式,目的是对最初平方根定义中的a给出平方根的符号表示.
(3)a的平方根记为±a后,选择例如“4的平方根是±2”的语句进行符号语言的改写,即±4=±2,使学生体验符号语言的简便.
7.根号的文字语言与符号语言的转化:
例3 说出下列式子的含义,并求值.
±9,4,-49,0,±0.
【设计意图】
概念符号化是概念教学的必要步骤,这使数学的表示形式更简明、清晰、准确,本例题让学生掌握概念符号的意义,并要进行数学符号和其意义的转换,以促进学生对数学符号意义的理解.
8.综合练习:
(1)16的平方根是;
(2)16的算术平方根是;
(3)16的平方根是;
(4)16的算术平方根是;
(5)的平方根是它本身;
(6)的算术平方根是它本身.
【设计意图】
这组练习将本堂课的重点内容进行了复习、巩固、检验,其中包含平方根与算术平方根的定义、平方根的性质和根号的意义.(1)与(2)、(3)与(4)是两组平行练习,用以区分平方根与算术平方根的概念,但后者考察点多了一个16的取值,思维需多转化一步,对于学生来讲就是一个陷阱,要提醒学生注意.
9.小结:
(1)这节课我们学习了一种新的运算,叫开平方,运算符号是根号.开平方与平方互为逆运算.曾经,我们还学过加法与减法互为逆运算,乘法与除法互为逆运算.我们可以借助逆运算求解或者检验.
(2)开平方与其他运算不同的是它的运算结果通常是两个,这是因为正数有两个平方根,它们互为相反数,不要遗漏,而算术平方根具有唯一性.
(3)本节新引入了一个符号——根号,要明确符号语言的含义,理解符号之间的对应关系.
(4)以前我们学过具有非负性的有绝对值和一个数的偶数次幂,今天我们又学习到两个具有非负性的内容,一个是开平方时被開方数a具有非负性,一个是a的算术平方根a具有非负性.
10.教后反思:
“平方根”这节课是一节典型的概念课,内容难度大,容量大,学生接受起来困难.本节课的重要概念是“平方根”,教学设计上侧重概念的生成过程和对概念的理解.概念的生成过程从正方形面积这个熟悉的情境入手,让学生感受到数学源于生活,大量举例,让学生直观感知概念,以此为基础再做概括.对于概念的理解不仅包括能利用概念判定什么是平方根,还要能剖析概念,认识它的性质,这样才能更清楚地掌握概念,所以本堂课在例1和探寻平方根性质时做了大量工作.概念符号化通常是概念教学的必要步骤,本节课注重文字语言与符号语言的转换,以促进学生对数学符号意义的理解.这节课的研究手法可供“立方根”参考、模仿.
本堂课考虑在此之前学生对数的认知只是有理数,所以被开方数都是开方后为有理数的数,但是在文字叙述上并未强调必须是这样的数,后续学生会明白任何非负数都有平方根.如果本堂课学生提出“5有平方根吗”这类问题,我们可以在交代完根号后给出肯定回答,而这样的数是什么数,可以先留悬念,待学完实数后就可以解答了.
结束语
数学教师要以数学核心素养为指导方针开展数学概念课教学,重视概念的生成,辨析概念的本质,深入挖掘概念的内涵与外延,最后将新概念迁入原有知识体系,完善数学知识网,帮助学生学好数学.
【参考文献】
[1]胡金燕.对“语文素养”内涵的探讨[J].课程教育研究(新教师教学),2014(26):13.
[2]朱传喜.努力提高大学生的数学素养[J].数学教育学报,2014(6):14-16.
[3]中华人民共和国教育部.义务教育课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[4]邝春莲.初中数学概念教学的思考与策略[J].读写算,2018(15):1.

