冲突证据的相关系数度量方法

孙贵东，关欣，衣晓，赵静

（海军航空大学航空作战勤务学院，山东 烟台 264001）

1 引言

复杂电磁环境和自然环境导致战场信息往往具有不确定性和高冲突性，多源信息融合技术通过各传感器的优势互补，融合各传感器的多源信息，提升系统的稳定性、可靠性和抗干扰能力，综合给出决策判定，在复杂战场环境下被广泛采纳。决策层融合作为信息融合的高层融合阶段，既可以处理同类传感器又可以处理异类传感器上报的信息，在不确定信息处理方面具有较大优势，得到了广泛研究。由于战场环境的复杂，这些决策信息本身携带不确定性，并且不同传感器之间的决策信息往往还是冲突的，因此，决策层融合的不确定信息处理问题是多源信息融合必须解决的问题，也是难点问题，并且是复杂战场环境的态势感知，威胁估计等决策判定的基础。信度函数[1-2]是决策层融合的一种重要方法，由于在不确定性数据处理领域尤其是对冲突信息处理方面的优势，已经成为雷达、通信等侦察数据的重要定量分析方法，也是最常用的决策层融合方法。2016年，国际近似推理期刊IJAR专门举办了信度函数专刊，庆祝信度函数40周年[3-4]，经过 40多年的发展，信度函数不仅在理论上不断完善，而且在聚类分析，模式分类和识别，多属性决策，图像处理，模糊集与粗糙集和近似推理等多个领域[5-10]也得到了广泛应用。

在信度函数发展的过程中，冲突证据度量是一个热点问题。自Zadeh[11]提出著名的Zadeh悖论以来，冲突证据度量就得到了国内外学者的广泛研究，并提出了各种冲突证据度量方法。由于传统的证据冲突系数k在高冲突情况下不能得到正确的融合结果，Smets等[12]提出了著名的TBM（transferable belief model），定义了Pignistic概率函数用来进行冲突证据度量；Jousselme等[13]提出了经典的Jousselme距离来度量冲突证据距离；文献[14-16]等系统性分析和比较冲突证据的各种距离度量方法；文献[17-18]等分别用冲突系数k和Jousselme证据距离的算术平均值和几何平均值度量冲突证据；文献[19]则基于证据虚假度进行冲突度量；而文献[20]基于类偏熵和关联熵定义了关联系数，来定量的表示证据之间的冲突；文献[21-22]利用夹角余弦来进行冲突度量；文献[23]基于Pignistic概率转换引入Tanimoto测度来度量冲突证据；文献[24-26]分别定义了证据重合度、新的证据不确定度和融合证据距离和证据散度的Hamacher T-余范度量冲突证据。

尽管上述文献在一定程度上实现了对冲突证据的度量，但是各种方法都或多或少存在局限性，比如Jousselme距离在证据完全冲突时，计算结果容易出现悖论；TBM在Pignistic概率转换过程中将信息平均分配给单类焦元，违背了单类互斥的原则，所以在后续的用 Pignistic概率距离计算冲突度量时也容易出现违背常理的结果。而现有的冲突证据度量方法大多是基于Jousselme距离和Pignistic概率转换的，因此新的冲突度量方法的提出是必要的。通过对现有冲突证据度量方法的分析得知，当证据为单类证据时，大多数方法都能够很好地度量，但是当证据为多类证据时，各种方法开始出现悖论。因此，多类证据的冲突度量是解决问题的关键，也是难点问题。尽管现有文献采用Jousselme距离中的矩阵D来拆分单类与多类证据，但是未考虑到单类与多类证据之间的矩阵D应该有所不同。

为此，本文基于关联系数提出一种冲突证据度量方法，目的是分清多类与单类证据之间的关系，并非是一种比现有方法具有很大优势的冲突证据度量方法，而是试图给出一种冲突证据度量的新思路。此外，相关系数作为序列线性变化的度量方法，已在多个领域体现优势，广义上，现有的夹角余弦度量是相关系数的一种向量表示方法，但是夹角余弦仅仅是线性向量的夹角，当向量维数增加时，从直观上无法分辨。并且，夹角余弦不能像相关系数一样可以从序列相关的角度进行分析，因此，本文方法亦即是现有夹角余弦冲突证据度量方法的改进和推广。

为此，本文首先概述信度函数理论，并进一步分析现有冲突证据度量方法，在此基础上提出冲突证据度量的相关系数方法，并重点讨论单类与多类证据之间的关系。最后通过经典的冲突证据分析算例验证所提出方法的有效性。

2 基本概述

2.1 信度函数概述

记辨识框架Θ上的任意命题A的基本信度赋值（BBA，basic belief assignment）或mass函数为其幂集2Θ到[0,1]上的映射m: 2Θ→ [ 0,1]，满足

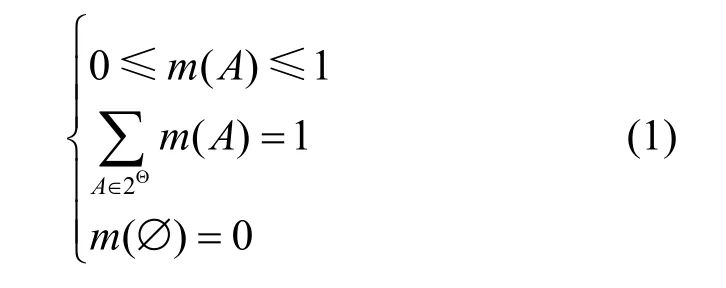
如 果m(A) ＞ 0 ， 称A为m(·)的 焦 元 ，则称A为主焦元，所有焦元集合构成了m(·)的核，记为κ(m)。m(A)的含义为幂集空间子集属于命题A的基本信度，命题A可以是单类（单集）也可以是多类（复合集）。

Shafer在mass函数的基础上定义了信度Bel(·)和似然度Pl(·)，对于幂集空间2Θ上的命题A、B，令A⊂B，则有

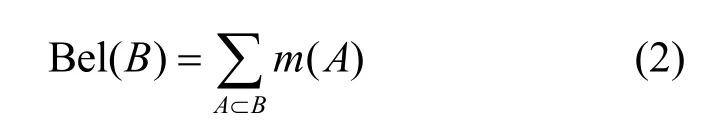
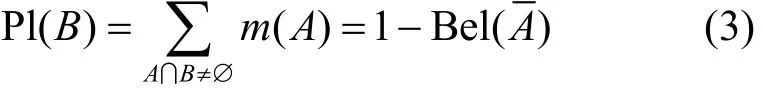
其中，是命题A在幂集空间的补集，易知Bel(B)≤ P l(B)，并记为命题B的不确定信度区间，信度函数通过信度区间描述不确定信息解决传统概率论不能解决的不确定信息处理的问题。而命题B的信度函数和似然函数定义为B到其信度 Bel(·)和似然度 Pl(·)上的映射。

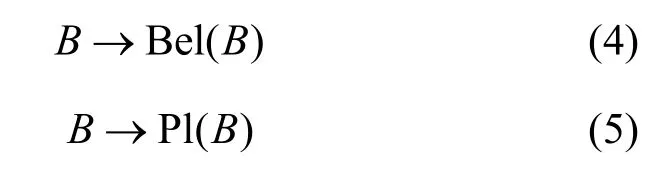
记同一辨识框架下，两条独立证据的 mass函数为m1(·)和m2(·)，A、B和C分别为辨识框架下的命题，称m(· ) =m1( ·) ⊕m2(·)为经典的DS组合规则满足

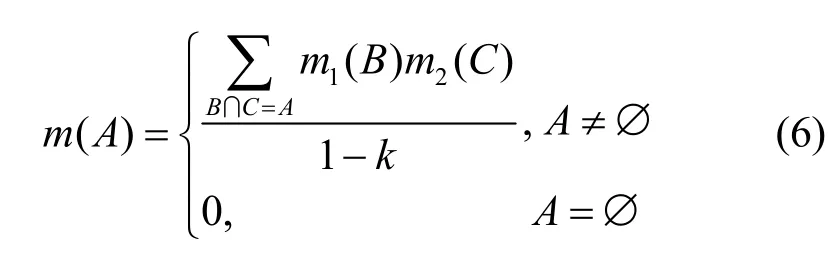
其中，k为两条证据的冲突程度，

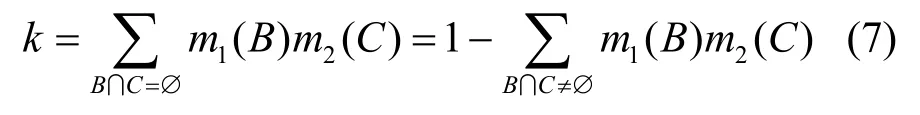
当k=1时，表示两条证据完全冲突，此时不能用经典的 DS组合规则进行融合，当k→1时，经典的DS组合规则融合后往往会产生违背直觉的结果，因此如何处理冲突证据是信度函数的一个重要研究方向。

2.2 现有冲突证据度量分析

2.2.1 Pignistic 概率距离

Smets等[12]提出了著名的 TBM 模型，定义了Pignistic概率函数。记辨识框架Θ上的证据对幂集空间命题的 mass函数为m，BetPm:Θ → [ 0,1]为Pignistic概率函数，满足

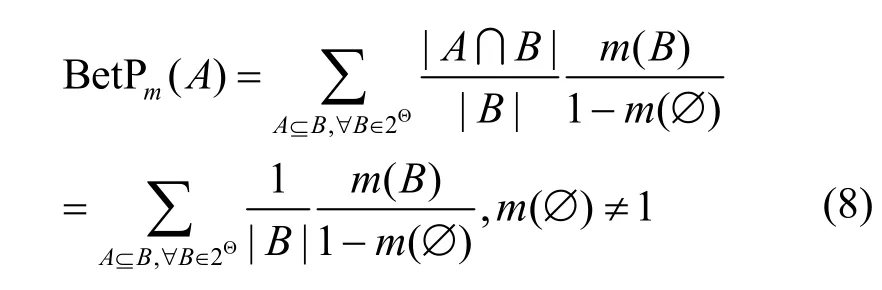
其中，|B|为焦元的势。BetPm(A)将复合类焦元的信度平均分配给了其包含的单类，是在香农信息熵意义下实现 mass函数到概率分布的转换。文献[27]在Pignistic概率函数的基础上提出了Pignistic概率距离

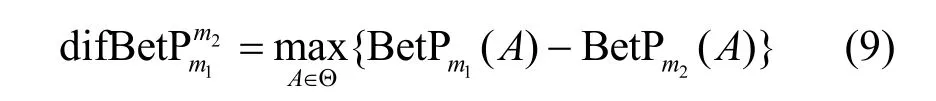
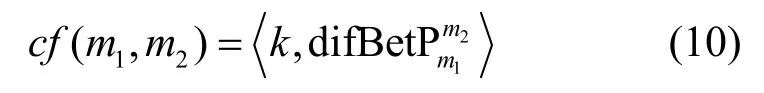
2.2.2 Jousselme 距离

Jousselme等[13]提出了经典的Jousselme距离。记相同辨识框架Θ上的2条证据对幂集空间命题的mass函数分别为m1和m2，dBPA(m1,m2)为Jousselme距离，满足

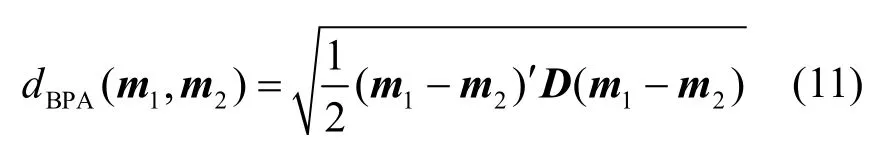
其中，m1、m2分别为mass函数在幂集空间张成的序列向量，D为 2|Θ|× 2|Θ|的正定矩阵，满足

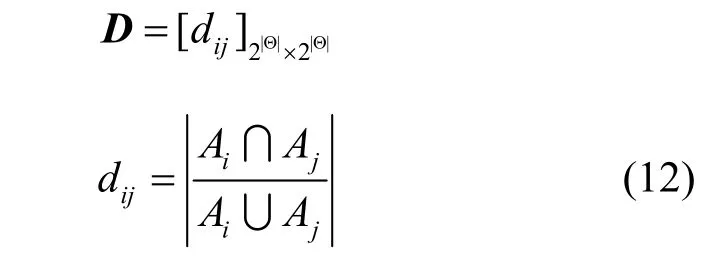
其中，Ai,Aj∈ 2Θ，矩阵D的概念十分重要，揭示了证据单集与多集命题之间的关系，有文献定义了新的矩阵D表达式，文献[14]中有具体的综述，可详细查看。

2.2.3 证据关联系数

邓勇等[20]基于类偏熵和关联熵定义了证据关联系数。记相同辨识框架Θ上的两条证据对幂集空间命题的 mass函数分别为m1和m2，r(m1,m2)为证据关联系数，满足

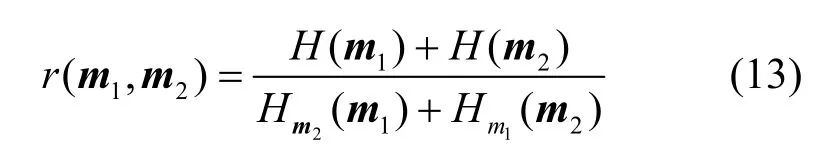
其中，H(m1)和Hm2(m1) 为随机变量m1关于随机变量m2的类偏熵，

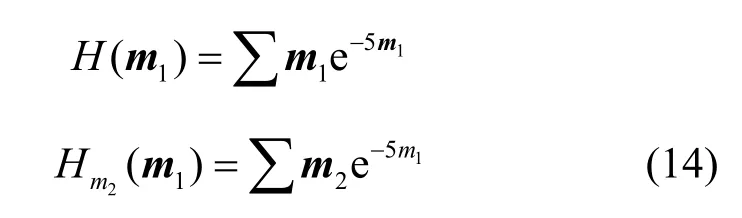
2.2.4 证据夹角余弦

宋亚飞等[21]和王路等[22]基于向量夹角余弦定义了证据夹角余弦。记相同辨识框架Θ上的两条证据对幂集空间命题的 mass函数分别为m1和m2，cos(m1,m2)为证据夹角余弦，满足

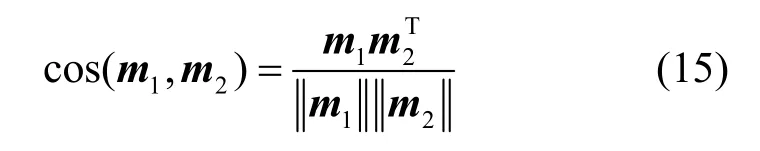
其中，m1和m2分别为证据mass函数m1和m2张成的向量，分别为m1和m2的模

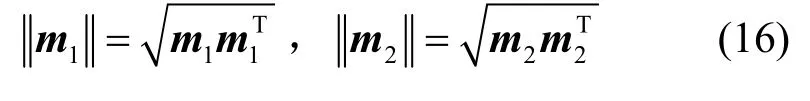
3 基于相关系数的冲突证据度量

证据冲突描述为证据对同一框架内相同命题基本信度的差异性，本文基于相关系数研究冲突证据度量问题。证据冲突与相关系数之间是逆向关系，证据冲突越大，相关性越小，反之亦然。本节首先给出相关定义，其次引入证据相关系数，最后重点分析单类和多类证据命题的关系，利用关系矩阵修正证据相关系数。

3.1 相关定义

定义1记辨识框架Θ上由两条证据mass函数组成的序列分别为和则证据相关定义为

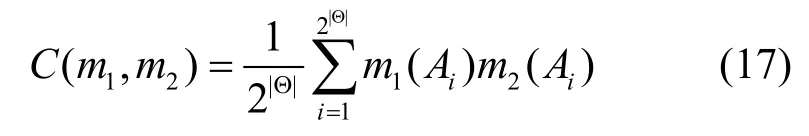
在实际计算过程中证据相关仅需计算存在焦元的证据之间的相关性，为此给出两条证据mass函数并核的概念，表示两条证据mass函数核的并集

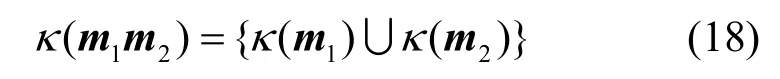
并 核 κ (m1m2)满 足为并核内焦元的个数，则证据相关修正为并核相关

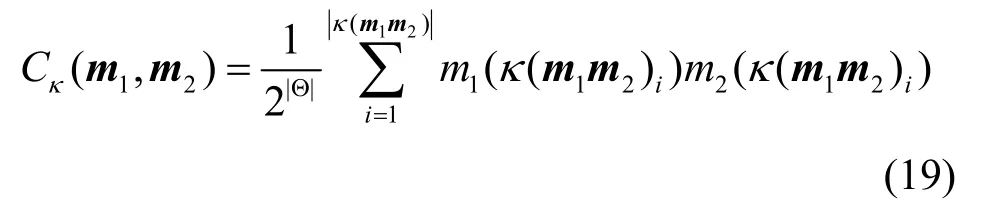
定义2在辨识框架Θ上，证据mass函数序列mk(·)的证据自相关定义为

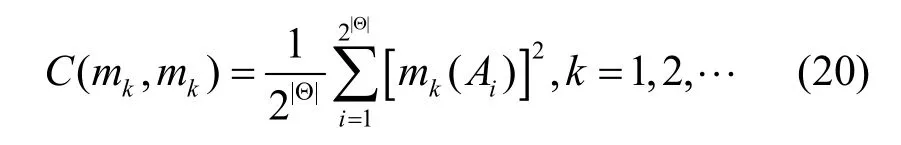
核自相关为

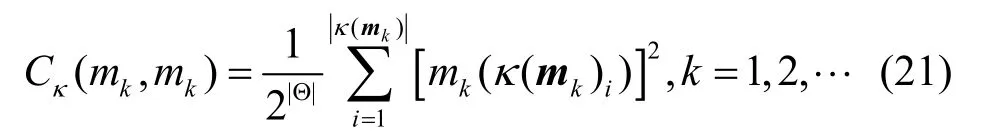
3.2 证据相关系数

定义 3 记辨识框架Θ上的两条证据对幂集空间命题的mass函数分别为m1和m2，ρ (m1,m2)为证据相关系数，表述为证据间线性变化的度量，满足

条件2)可以具体描述为下述重要定理。

定理在证据理论框架内，证据线性相关等价于证据相等。

证明1如果而 mass函数满足则即

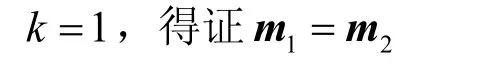
如果，m1=m2，由相关系数含义可知，显然ρ(m1,m2)=1。

证毕。

实际上，正是由于上述定理才使相关系数可以作为证据冲突的度量方法，如果脱离的证据理论框架，相关系数仅描述线性关系，不能够充分描述变量间的接近度。

定义4在辨识框架Θ上，两条证据mass函数序列为m1(·)和m2(·)，证据相关系数定义为归一化的证据相关，可以用式(22)表示。

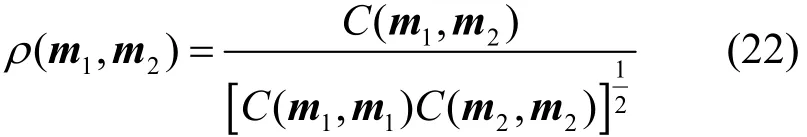
将证据相关系数修正为并核相关系数为

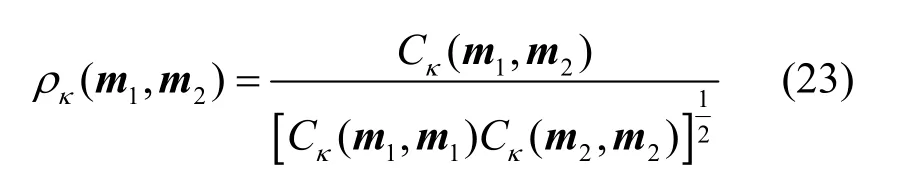
上述相关系数满足相关系数的3条准则。

证明2

1) ρκ(m1,m2) = ρκ(m2,m1) 显然成立。

2) ρκ(m1,m2) =1,当 且仅当m1=m2在证明1中已经给出。

3) 由于m1≥ 0 ,m2≥ 0 ，所以 ρκ(m1,m2)≥ 0，

证毕。

例1辨识框架 Θ = { θ1,θ2, θ3, θ4, θ5}，3条独立证据分别为

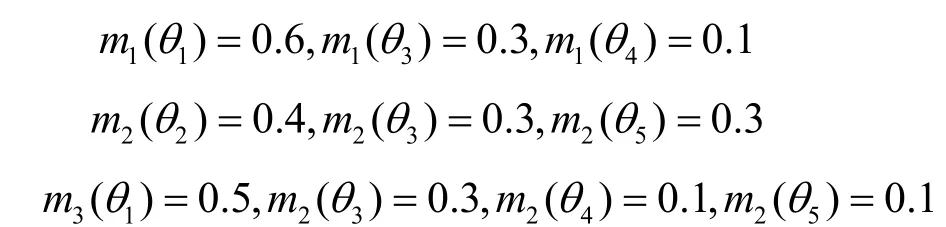
通过计算得知证据m1和m2以及m1和m3之间的相关系数分别为

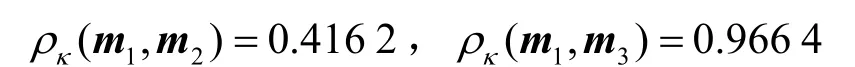
计算结果与事实情况相符，验证了所提出的冲突证据相关系数度量的准确性。

3.3 证据相关系数修正

上述证据相关系数在处理辨识框架Θ上仅存在单类命题时优势明显，但是如果单类和多类命题共同存在时，上述证据相关系数无法很好地处理。

例2辨识框架 Θ = { θ1,θ2, θ3, θ4, θ5}，3条独立证据分别为

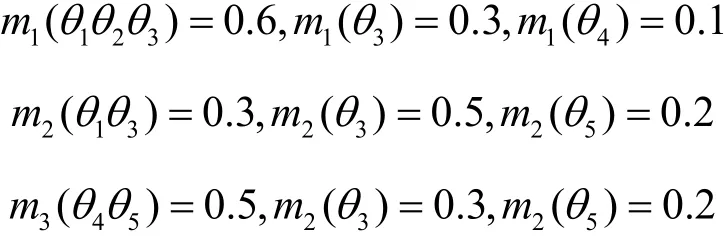
通过计算得知证据m1和m2以及m1和m3之间的相关系数分别为

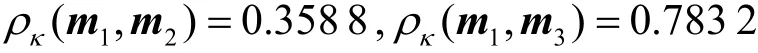
显然计算结果与事实情况不符，m1和m2之间的相关性应该比m1和m3之间相关性要强。

上述违背常理的结果是未区分证据单类与多类命题导致的，实际上，证据冲突度量的难点在于相关计算过程中，如何分清单类命题与多类命题。因此，基于文献[13]的思想，引入关系矩阵的概念，分清单类命题与多类命题。

定义5记辨识框架Θ上，2条证据mass函数分别为文献[13]给出的证据关系矩阵为其中，d描ij述辨识框架内命题间的相互关系。在计算过程中，仅需分清证据 mass函数并核单类与多类之间的关系即可，为此定义并核证据关系矩阵为

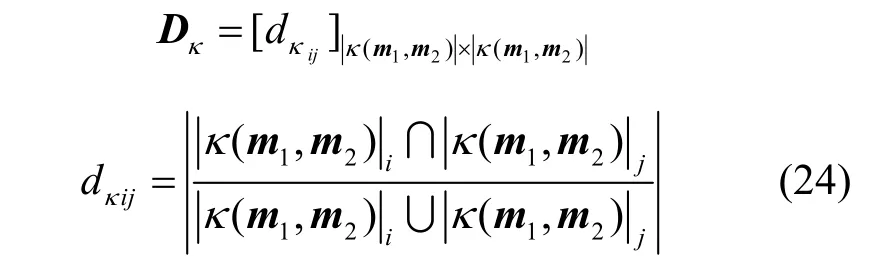
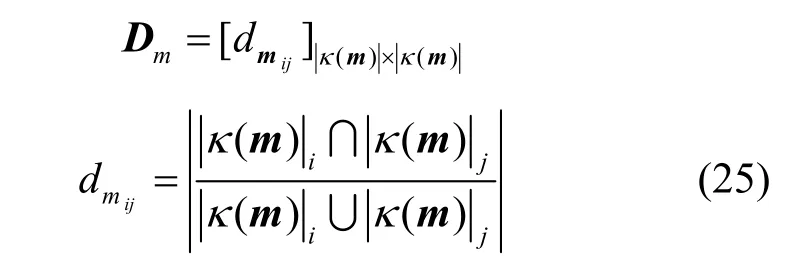
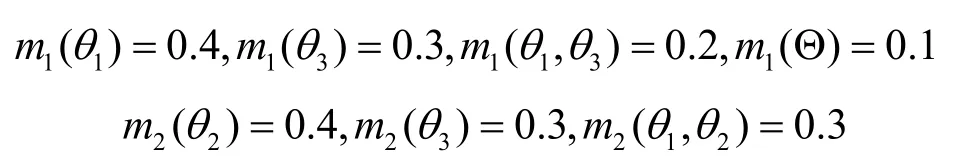
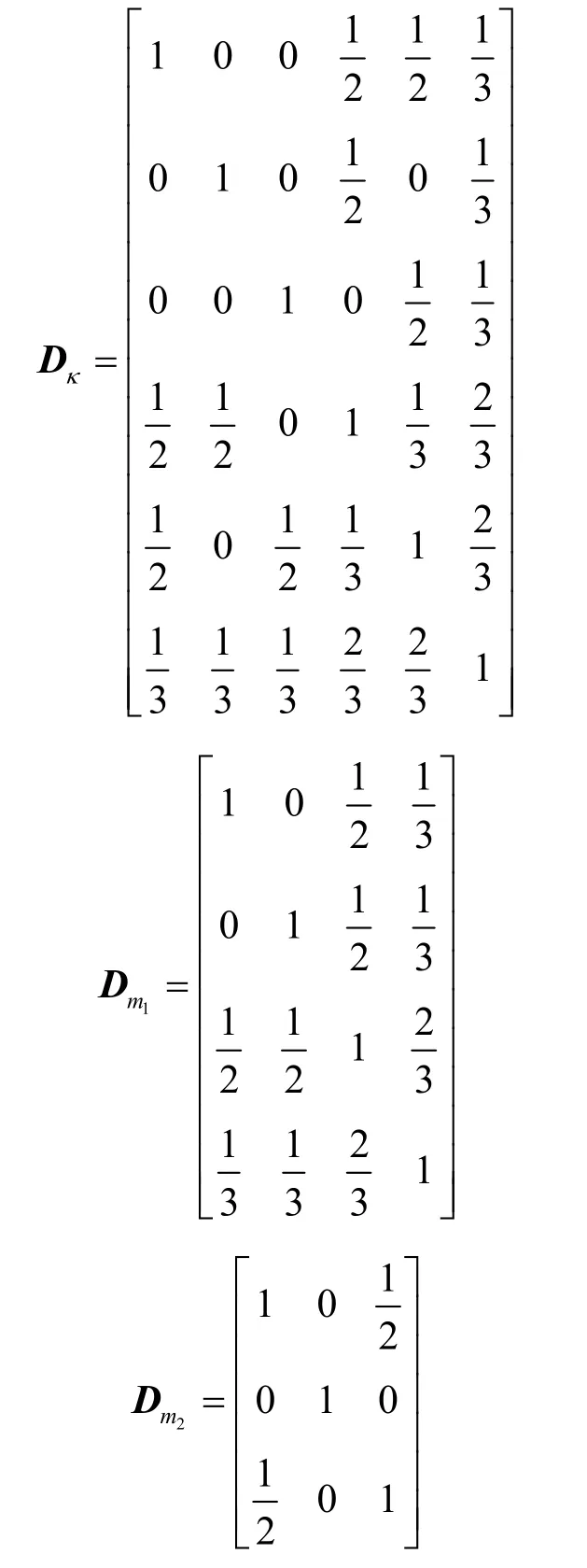
尽管证据关系矩阵一定程度上解决了证据冲突度量的问题，文献[13,21-22]等都采用了证据关系矩阵的思想，但是上述方法都存在不足。主要原因在于，一方面，证据关系矩阵修正的对象不准确。文献[21-22]利用关系矩阵先修正证据mass函数得到新的mass函数，再利用新的mass函数计算相关系数作为冲突度量，此类方法修正的对象不准确，关系矩阵应该作用于证据的相互关系而不是mass函数，这与文献[13]提出关系矩阵时的思想一致。此外先修正证据mass函数，会导致得到的新的mass函数的含义不清楚，并且不再满足新mass函数之和小于1的条件。另一方面，在证据冲突度量计算过程中，未分清并核与核之间的单类与多类的关系。并核与核之间的单类与多类的证据关系矩阵应该有所区别，并核证据关系矩阵应该修正并核之间单类与多类的关系，而不能修正核之间单类与多类的关系，否则会造成后续的度量错误，此时应该用核证据关系矩阵修正核之间单类与多类的关系。

例 4 方便起见，这里采用例 3的数据进行说明。

如果采用现有的夹角余弦方法，直接用关系矩阵修正证据mass函数得到新的mass函数，则有

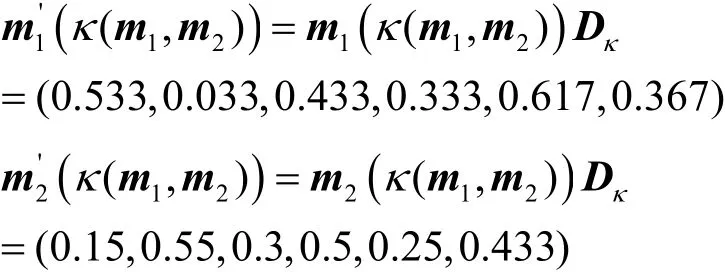
在上述分析的基础上，综合考虑关系矩阵作用的对象，以及用于并核与核的关系矩阵应该有所区别，提出一种证据作用中修正方法，在证据相关计算过程中，直接用并核证据关系矩阵和核证据关系矩阵修正，形成修正后的并核相关CDκ(m1,m2)和核自相关CDκ(mk,mk)

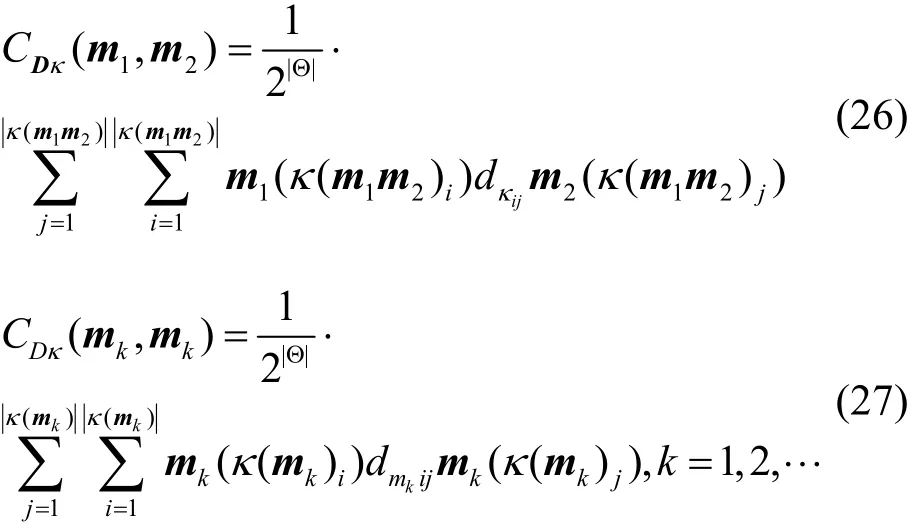
式(26)和式(27)用向量形式分别表示为

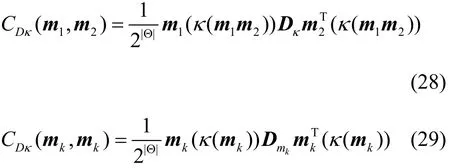
其中，m1( κ(m1,m2))和m2( κ(m1,m2))分别为并核mass函数张成的向量，mk( κ(mk))为核mass函数张成的向量。

按上述方法修正后的相关系数为

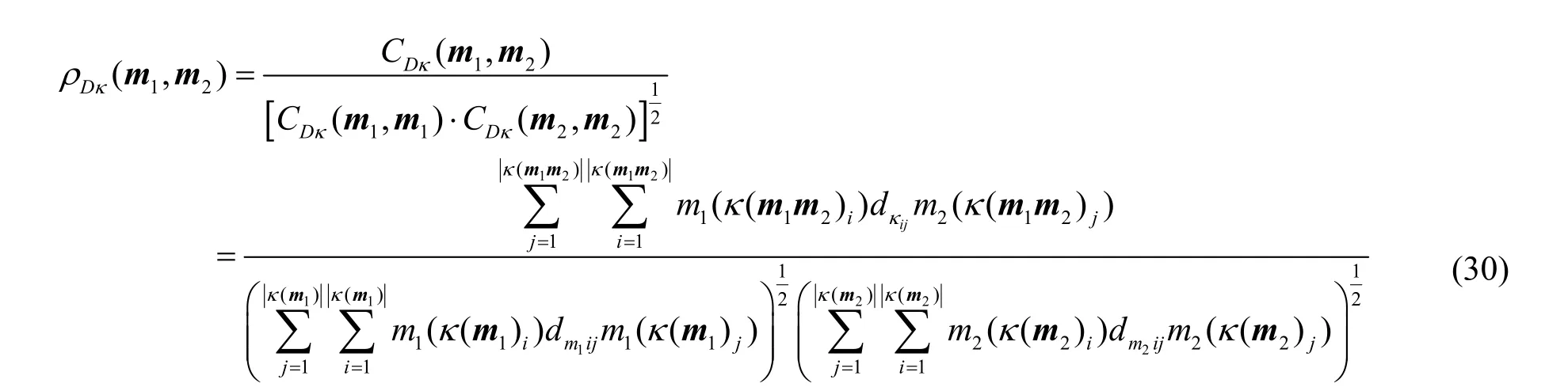
式(30)用向量式表示为

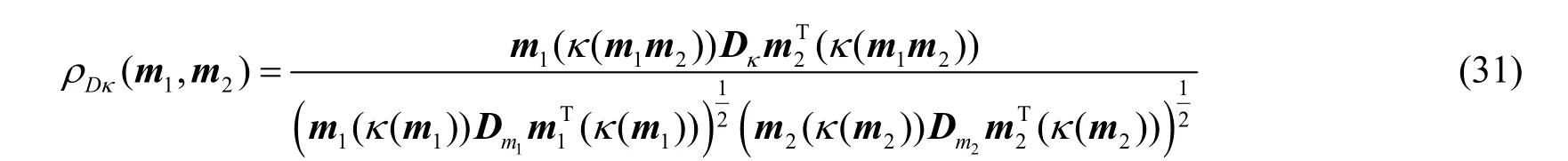
注意到，式(13)与文献[14]中和文献[21]中的定义的夹角余弦等有相似之处，但是相比夹角余弦，式(31)一方面分清了单类与多类之间的关系，用不同的关系矩阵进行拆分，另一方面，虽然计算系数因子被约简，但是在相关计算过程中一直保留，特别当辨识框架类别重要性不同时，此因子可以看作权重系数，保证了计算准确性，是夹角余弦框架所不能处理的，因此，此方法可以说是现有夹角余弦方法的改进和推广。

基于上述相关系数得到冲突证据度量表达式为

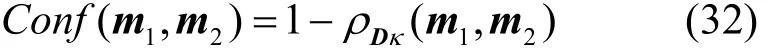
4 算例分析

本节采用两组算例对所提出的冲突证据度量方法进行验证，第一组算例采用与例2相同的数据进行验证，第二组算例采用现有文献中经常采用的文献[13]中的经典算例，对冲突证据度量进行验证并对比分析。

算例 1在复杂战场环境下的多源信息融合系统中，我方电子侦察系统侦测到一未知目标抵进我海域，机载雷达、ESM和IFF这3类传感器各自对此未知目标进行识别判断得到以下决策信息。未知目标的可能识别类为1θ、2θ、3θ、4θ、5θ，传感器对未知目标可能的识别类的决策判定信息分别为：机载雷达认为是1θ、2θ和3θ之中的某目标的可能性为60%，其中，有30%的把握判定为目标3θ，判定为目标4θ的可能性只有10%；ESM认为是1θ和2θ之中的某目标可能性为 30%，其中，50%的把握判定为目标θ3，20%的把握判定为θ5；而IFF判定为目标θ4或目标θ5的可能性为50%，其中，有30%的把握判定为目标θ5，另外认为是目标θ3的可能性为30%。信息融合决策中心为实现目标的识别判定，需要对三类传感器的决策信息进行融合判定，由各传感器的决策信息得知，其决策信息之间是矛盾和冲突的，为此决策判定前需要对其进行冲突度量处理，以更好地进行下一步的融合判定。

上述实例可抽象为下述数学语言。

互斥且完备的辨识框架为 Θ = { θ1, θ2, θ3, θ4, θ5}，三条独立证据分别为

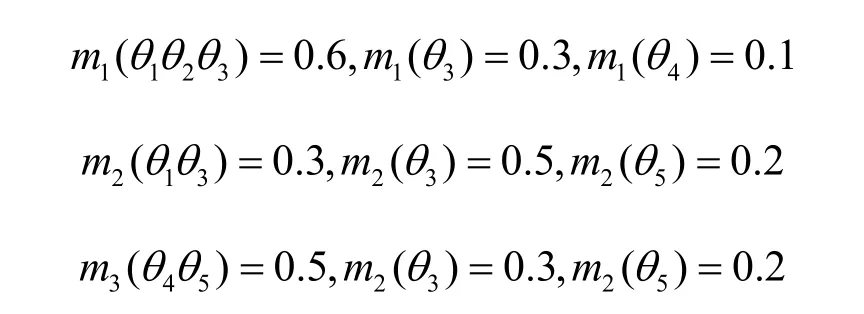
为实现冲突证据的融合处理问题，首先需对上述证据进行冲突度量，利用本文方法分别计算证据m1和m2以及m1和m3之间的冲突度，计算步骤如下所示。

证据m1和m2的并核为，对应的mass函数分别为

证据m1和m3的并核为θ1θ2θ3, θ4θ5} ，对应的mass函数分别为

m1和m2，m1和m3之间的并核关系矩阵以及m1，m2，m3自身的关系矩阵分别为

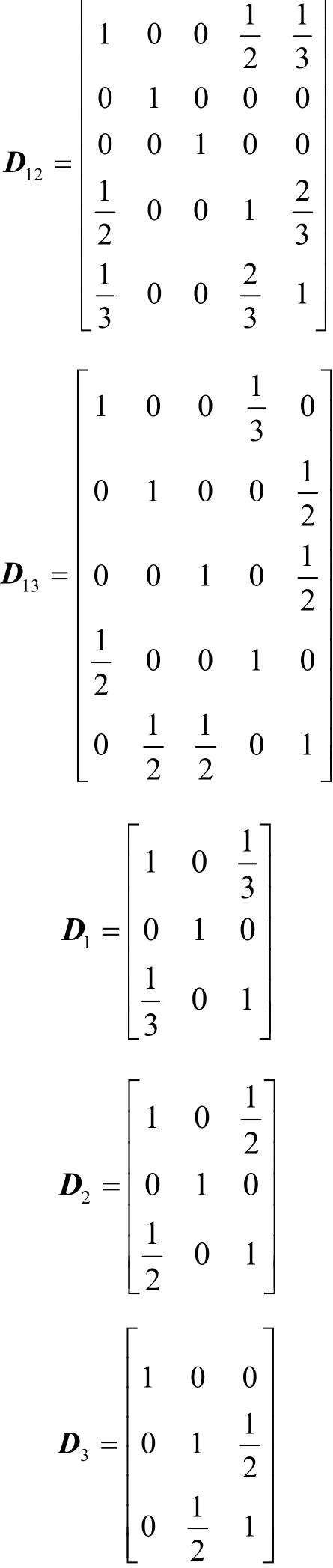
利用式（31）和式（32）计算得到证据m1和m2以及m1和m3之间的冲突度分别为

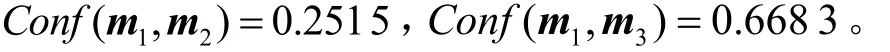
该算例计算结果与事实情况相符，纠正了例 2计算结果的不足，得到了更准确的冲突度量。

由于本文主要研究内容为冲突证据融合的度量问题，在度量的基础上可以采用现有的方法进行识别判定。此外新的冲突证据融合方法也是信度函数理论的一个急需解决的内容，在未来的研究中会继续探讨，这里不再赘述。

算例 2记互斥且完备的辨识框架 Θ ={θ1, θ2,…, θi,… , θ20}，两条独立的证据对命题的mass函数分别为的子集。

假设A从θ1，依次增加一个元素，直至A=Θ，变化规律简记为{1}，{1,2},…,{1,2,…,20},在变化过程中分别利用传统证据冲突系数k，Jousselme距离dBPA，Pignistic概率距离，证据关联系数r，夹角余弦cos，冲突系数k和Jousselme证据距离的算术平均值kd以及本文提出的相关系数Conf度量mass函数m1和m2之间的冲突程度，计算结果分别如图1和表1所示。

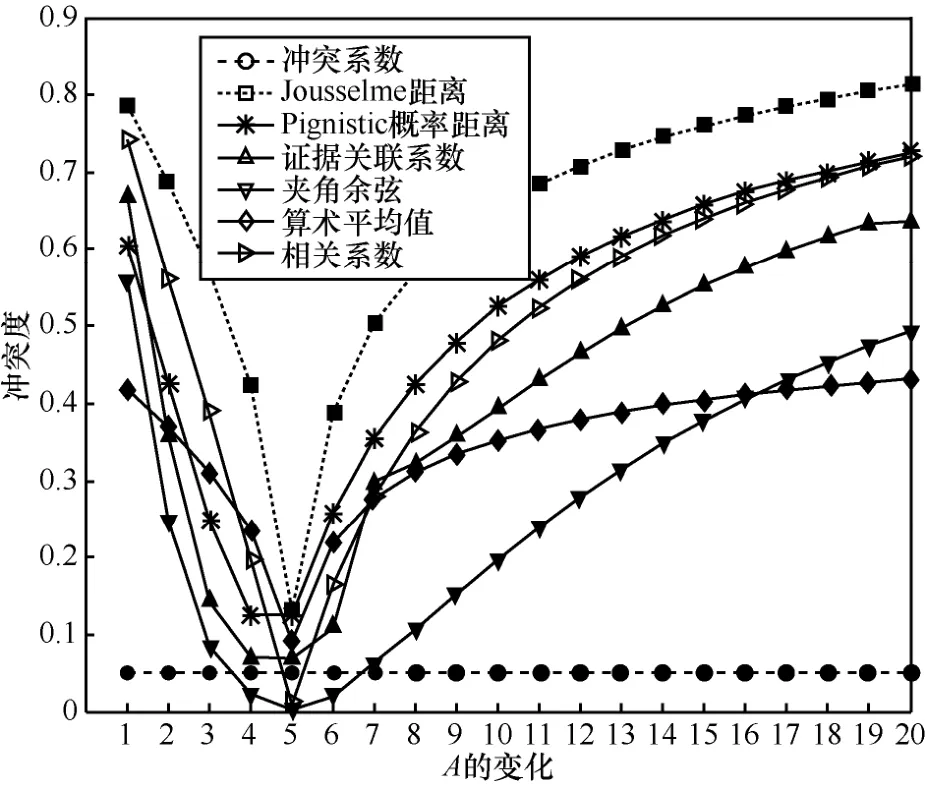
图1 冲突证据度量对比

通过图1和表1的形象对比可知，当A按规律从{1}变化到{1,2,…,20}时，只有冲突系数k维持不变，显然违背事实情况，说明k不能很好地对冲突证据进行度量。其余6种方法变化规律则一致，都随着A的变化先减小至A= { 1,2,3,4,5}为止，此时证据间的冲突最小，这与事实相符，此时两条证据都对命题{1,2,3,4,5}具有较高的信度，因此此时的冲突度最小，并且当A继续变化，冲突度逐渐增加，也与两条证据对命题信度差异变大的事实相符。所以，通过此经典的冲突证据度量算例，验证了本文提出的相关系数冲突证据度量方法的有效性。

5 结束语

本文从相关系数的角度给出了冲突证据度量的一种思路，定义归一化的证据相关为证据相关系数，以此作为冲突证据度量。在此基础上，基于现有的关系矩阵重点讨论多类与单类的分辨问题，认为并核与核的关系矩阵应当有所区分，定义并核关系矩阵作用于并核证据，核关系矩阵作用于核证据。通过并核与核关系矩阵的修正，得到了新的的冲突证据度量公式，能够处理多类证据的冲突度量问题，克服了现有夹角余弦方法的局限性，具有分辨性好，准确率高的优点。最后结合经典的冲突证据算例验证了提出的冲突证据相关系数度量方法的有效性。

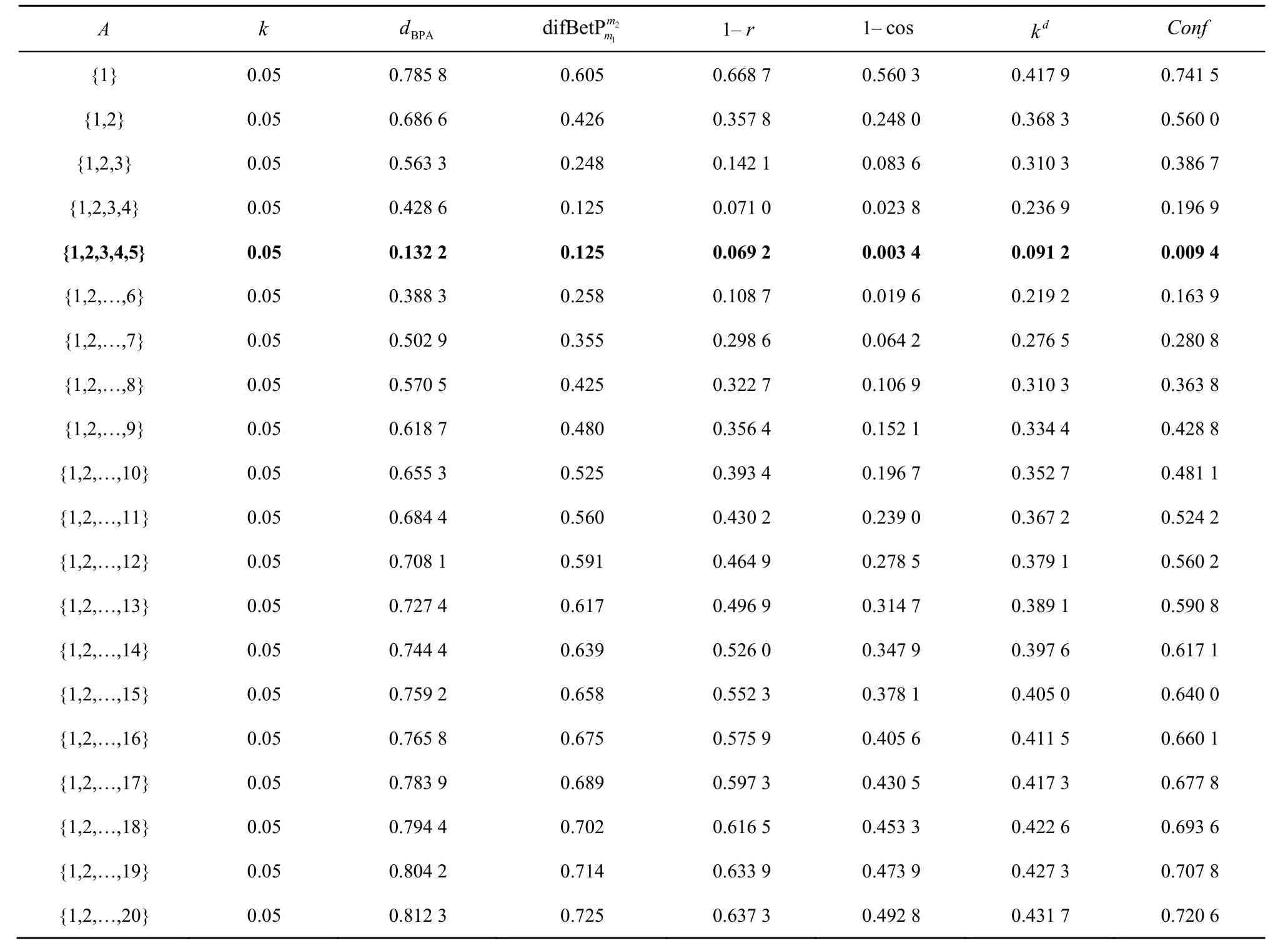
表1 冲突证据度量对比